初中数学青岛版 七年级下册13.2 多边形同步课件(共63张PPT)
文档属性
| 名称 | 初中数学青岛版 七年级下册13.2 多边形同步课件(共63张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 66.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 19:50:27 | ||
图片预览









文档简介
(共63张PPT)
第13章
平面图形的认识
青岛版 七年级下册
13 . 2
多边形
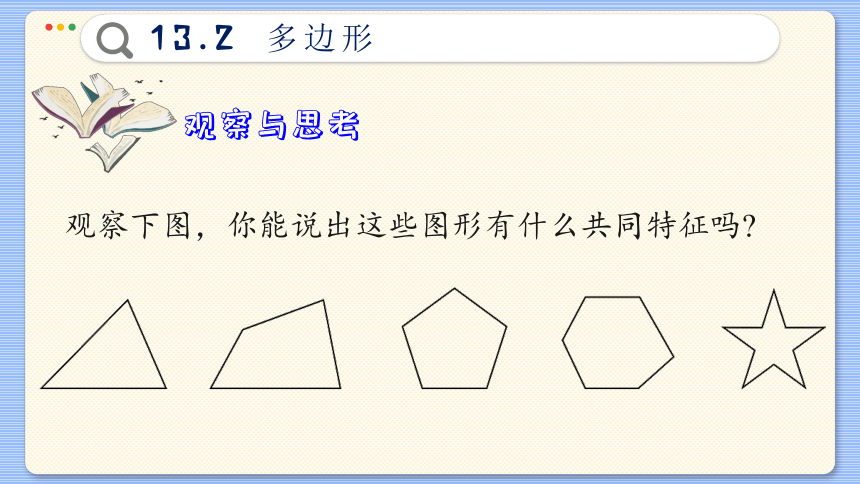
观察与思考
观察下图,你能说出这些图形有什么共同特征吗
平面内,若干条线段首尾顺次相接,且有公共端点的线段不在同一条直线上,这样得到的图形叫做多边形.
组成多边形的各条线段叫做多边形的边,它们的公共端点叫做多边形的顶点,相邻两条边所组成的角叫做多边形的内角,简称多边形的角.
一个多边形有四条边,叫做四边形;
有五条边,叫做五边形;
一般地,有n条边,叫做n边形(n是大于2的整数).
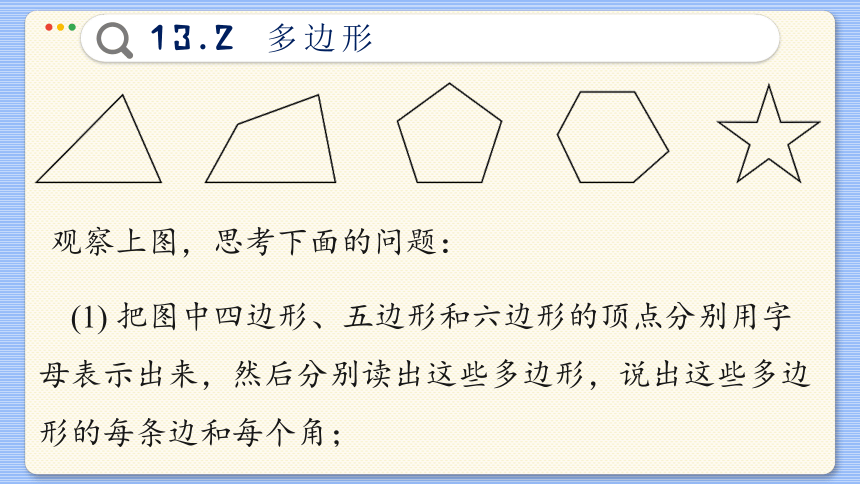
观察上图,思考下面的问题:
(1) 把图中四边形、五边形和六边形的顶点分别用字母表示出来,然后分别读出这些多边形,说出这些多边形的每条边和每个角;
三边形习惯上叫做三角形,它是边数最少的多边形.
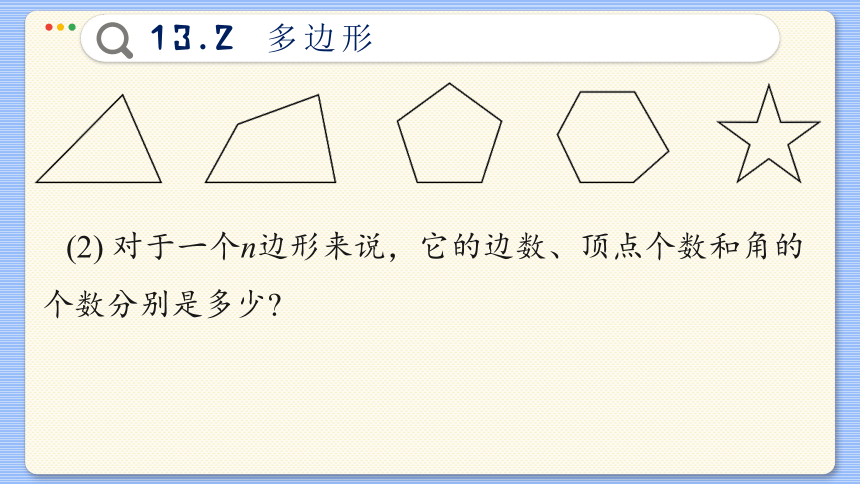
(2) 对于一个n边形来说,它的边数、顶点个数和角的个数分别是多少
(3) 分别连接图中四边形、五边形、六边形不相邻的任意两个顶点,得到哪些线段
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
对角线
(4) 数一数,四边形一共有几条对角线 五边形呢 六边形呢
分别度量图中每个多边形的边和角,你发现它们具有什么特点
各边相等,各角也相等的多边形叫做正多边形.
正三角形
(等边三角形 )
正方形
(正四边形)
正五边形
正六边形
正八边形
挑战自我
你能用若干个(个数不限)同样大小的含 45°的三角尺拼成四边形吗 这些四边形内角度数有几种不同情况 试一试.
两个同样大小的含45°的三角形尺能拼成一个正方形或一个平行四边形,
如下图:
正方形的四个角都是90°
平行四边形的内角为45°和135°
故拼成的四边形内角度数有90°、45°135°三种情况
智趣园
多边形有两类:一类是凸多边形,它的每个内角都小于 180°例如我们认识的三角形、平行四边形、梯形、正多边形都是凸多边形;另一类是凹多边形,它的内角中至少有一个大于180°.
锦 旗
如图是一面锦旗的图片,它是一个凹五边形.你能找出它的哪个内角大于180°吗
五角星形是凹多边形吗
你能分别画出一个凹四边形和凹六边形吗 试试看.
锦 旗
练 习
1. 举出生活中多边形的实例.
多边形:由三条或三条以上的线段首尾顺次连接所组成的平面图形.
生活中的多边形有被套、餐桌、地砖等.
2. 图中的多边形是几边形 说出它的边、顶点与内角.
略
3. 如图,画出正五边形ABCDE的所有对角线.
略
实验与探究
(1) 一个正方形的内角和是多少度 一个长方形呢
一个正方形的内角和是360°,
一个长方形的内角和是360°;
(2) 在纸上任意画出一个四边形 ABCD .将四边形的四个内角剪下来 ,
并将剪下来的各个内角按中图所示的方式拼在一起,你有什么发现
在图中∠1,∠2,∠3,∠4有公共的顶点,相邻的角有一条公共边,它们恰好拼成了一个周角,所以四边形ABCD的内角和是360°
(3) 除了利用上面的实验方法外,利用三角形的内角和的性质,能说明四边形的内角和是360°吗
为了解决问题的需要,在原来图形上添画的线叫做辅助线.
辅助线通常画成虚线.
小资料
如图,在一个任意的四边形ABCD内任取一点O,
连接AO,BO、CO、DO,
得到△OAB,△OBC,△OCD和△ODA.
这四个三角形所有内角之和为 4 × 180°,比四边形ABCD的内角和多出了以O为顶点的四个角之和,即360°.
从而,可以得出任意四边形的内角和等于:
4×180°-360°= 360°.
(4) 用上面的方法,你能求出任意五边形的内角和吗
(5) 如果O是n边形A1A2A3 ··· An-1An内的一点连接 OA1,OA2,···,OAn-1,OAn,
你能利用△OA1A2,△OA2A3,···,△OAn-1An,△OAnA1 的所有内角的度数之和,推导出n边形A1A2A3
··· An-1An 的内角和吗 与同学交流.
n边形的内角和等于(n- 2)·180°
观察与思考
你还记得什么是三角形的外角吗 三角形外角的意义可以推广到多边形上.
多边形一个角的一边与另一边的反向延长线所组成的角,叫做多边形的外角.
任意画出一个四边形ABCD.思考下面的问题:
(1) 从四边形ABCD的任意一个顶点 (例如顶点C)处,画四边形的外角.
你能画出几个 它们具有什么
位置关系和数量关系
(2) 四边形ABCD共有多少个外角
(3) 四边形ABCD的一个外角跟与它相邻的内角有什么数量关系
(4) 如图 ,在四边形ABCD的每个顶点处分别画出它的一个外角这些外角的和是多少 你是怎样得到这个结果的 五边形呢 六边形呢
四边形ABCD的每个外角都与相邻的内角组成一个平角.
四边形有4个内角,组成的四个平角的和是4×180°.
再减去四边形的内角和360°,因此这4个外角的和为360°.
一般地,在多边形的每个顶点处分别取多边形的一个外角, 这些外角的和叫做多边形的外角和.
多边形的外角和
如图所示,∠1, ∠2,∠3,∠4的和就是四边形ABCD的外角和四边形的外角和等于360°.
(5) n边形的外角和是多少 说明你的理由.
n边形的每一个内角跟与它相邻的一个外角都组成一个平角,n边形有n个内角,所以,这些平角的和为n·180°,其中所有内角的和为 (n-2)·180°,因此n边形的外角和为:
n·180°-(n - 2)·180°
= n·180°-n·180°+2×180°
=360°
多边形的外角和等于360°.
挑战自我
任意多边形的内角中,最多有几个锐角 说明理由.
由于n边形外角和为360°,则外角中至多有三个钝角,因此n边形内角中最多有三个锐角.
练 习
1. 分别计算九边形、十二边形、二十边形的内角和.
九边形的内角和为:(9-2) ×180°=1260°
十二边形的内角和为:(12-2) ×180°=1800°
二十边形的内角和为:(20-2) ×180°=3240°.
2. 求正八边形的每个内角与每个外角的度数.
每个内角为135°,每个外角为45°.
习题 13.2
复习与巩固
1. 把n边形内的任意一点与各顶点相连接,这些线段把n边形分成多少个三角形 把n边形一边上的任意一点(不是顶点)与其他边上的各顶点相连接,这些线段把n边形分成多少个三角形
把n边形内的任意一点与各顶点相连接这些线段把n边形分成(n-2)个三角形;
把n边形一边上的任意一点(不是顶点)与其他边上的各顶点相连接这些线段把n边形分成(n-1)个三角形.
2. 如果一个多边形从一个顶点出发的对角线把这个多边形分成6个三角形,这个多边形是几边形
设这个多边形的边数是n,
由题意得,n-2=6.
解答n=8.
答:这个多边形是八边形.
3.下面的说法正确吗 如果不正确,你能用一个例子作出说明吗
(1) 如果一个多边形的各边都相等,那么它是正多边形;
如果一个多边形的各边都相等,那么它是正多边形,说法错误,菱形的各边都相等,但菱形不是正多边形;
(2) 如果一个多边形的所有内角都相等,那么它是正多边形.
如果一个多边形的所有内角都相等,那么它是正多边形,说法错误,矩形的四个角都是直角但矩形不是正多边形.
4. 正三角形、正方形、正五边形、正六边形的一个内角各是多少度
根据多边形的内角和公式可得:
正三角形的内角和为: (3-2) ×180°=180°,
∴正三角形的每一个内角为180°÷3=60°
正方形的内角和为:(4-2) ×180°=360°,
∴正方形的每一个内角为360°÷4=90°;
正五边形的内角和为:(5-2) ×180°=540°,
∴正五边形的每一个内角为540°÷5=108°;
正六边形的内角和为:(6-2) ×180°=720°,
∴正六边形的每一个内角为720°÷6=120°.
5. 一个多边形的内角和为 2700°,求它的边数.
设这个多边形的边数为n.
由题意得:(n-2) ×180°=2700°
解得 n=17.
即这个多边形的边数为17.
6. 一个多边形的内角和与外角和相等,这个多边形是几边形
设这个多边形的边数为n.
由题意得:(n-2) ×180°=360°
解得n=4.
即这个多边形是四边形。
拓展与延伸
7. 如图,五角星中含有几个五边形 几个四边形 几个三角形 把它们分别表示出来.
略
8. 能不能找出一个多边形,使它的每一个内角都是与它相邻外角的3倍
能,这个多边形是正八边形.
每一个外角的度数:180°÷4=45°,
360÷45=8.
这个多边形是正八边形
探索与创新
9. (1) 四边形ABCD中,从顶点A引对角线AC,将四边形分为几个三角形 这几个三角形所有内角之和与四边形内角之和有什么关系
由图形可知,从顶点A引对角线AC,将四边形分成2个三角形,这2个三角形所有内角和等于四边形内角之和;
(2) 五边形ABCDE中,过顶点A最多能引几条对角线 它们将五边形分为几个三角形 这几个三角形所有内角之和与五边形内角之和有什么关系
五边形ABCDE中,从顶点A最多能引2条对角线,它们将五边形分成3个三角形,这3个三角形所有内角和等于五边形内角之和;
(3) 过n边形的任意一个顶点最多可引几条对角线 它们将n边形分为几个三角形这几个三角形所有内角之和与n边形内角之和有什么关系 由此你能得出n边形内角之和的公式吗 试一试.
过n边形的任意一个顶点最多可以 (n-3)条对角线,它们将n边形分为 (n-2) 个三角形,这(n-2)个三角形所有内角之和等于n边形内角之和,由此可得出n边形内角之和的公式为 (n-2)×180°
10. 四边形的边比三角形的边多了一条,内角和多了多少度 五边形的边比四边形的边多了一条,内角和多了多少度 由此可以推测,多边形的边每多一条,内角和多了多少度 说明你的理由.
四边形的边比三角形的边多了一条,内角和多了 360°-180°=180°,
五边形的边比四边形的边多了一条,内角和多了540°-360°=180°,
由此可以推测,多边形的边每多一条,内角和多了180°,
∵多边形的内角和为: (n-2)×180°.
∴若多边形边数每多一条,则它的内角和多了
(n+1-2) ×180°- (n-2) ×180=180°.
本课结束!
第13章
平面图形的认识
青岛版 七年级下册
13 . 2
多边形
观察与思考
观察下图,你能说出这些图形有什么共同特征吗
平面内,若干条线段首尾顺次相接,且有公共端点的线段不在同一条直线上,这样得到的图形叫做多边形.
组成多边形的各条线段叫做多边形的边,它们的公共端点叫做多边形的顶点,相邻两条边所组成的角叫做多边形的内角,简称多边形的角.
一个多边形有四条边,叫做四边形;
有五条边,叫做五边形;
一般地,有n条边,叫做n边形(n是大于2的整数).
观察上图,思考下面的问题:
(1) 把图中四边形、五边形和六边形的顶点分别用字母表示出来,然后分别读出这些多边形,说出这些多边形的每条边和每个角;
三边形习惯上叫做三角形,它是边数最少的多边形.
(2) 对于一个n边形来说,它的边数、顶点个数和角的个数分别是多少
(3) 分别连接图中四边形、五边形、六边形不相邻的任意两个顶点,得到哪些线段
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
对角线
(4) 数一数,四边形一共有几条对角线 五边形呢 六边形呢
分别度量图中每个多边形的边和角,你发现它们具有什么特点
各边相等,各角也相等的多边形叫做正多边形.
正三角形
(等边三角形 )
正方形
(正四边形)
正五边形
正六边形
正八边形
挑战自我
你能用若干个(个数不限)同样大小的含 45°的三角尺拼成四边形吗 这些四边形内角度数有几种不同情况 试一试.
两个同样大小的含45°的三角形尺能拼成一个正方形或一个平行四边形,
如下图:
正方形的四个角都是90°
平行四边形的内角为45°和135°
故拼成的四边形内角度数有90°、45°135°三种情况
智趣园
多边形有两类:一类是凸多边形,它的每个内角都小于 180°例如我们认识的三角形、平行四边形、梯形、正多边形都是凸多边形;另一类是凹多边形,它的内角中至少有一个大于180°.
锦 旗
如图是一面锦旗的图片,它是一个凹五边形.你能找出它的哪个内角大于180°吗
五角星形是凹多边形吗
你能分别画出一个凹四边形和凹六边形吗 试试看.
锦 旗
练 习
1. 举出生活中多边形的实例.
多边形:由三条或三条以上的线段首尾顺次连接所组成的平面图形.
生活中的多边形有被套、餐桌、地砖等.
2. 图中的多边形是几边形 说出它的边、顶点与内角.
略
3. 如图,画出正五边形ABCDE的所有对角线.
略
实验与探究
(1) 一个正方形的内角和是多少度 一个长方形呢
一个正方形的内角和是360°,
一个长方形的内角和是360°;
(2) 在纸上任意画出一个四边形 ABCD .将四边形的四个内角剪下来 ,
并将剪下来的各个内角按中图所示的方式拼在一起,你有什么发现
在图中∠1,∠2,∠3,∠4有公共的顶点,相邻的角有一条公共边,它们恰好拼成了一个周角,所以四边形ABCD的内角和是360°
(3) 除了利用上面的实验方法外,利用三角形的内角和的性质,能说明四边形的内角和是360°吗
为了解决问题的需要,在原来图形上添画的线叫做辅助线.
辅助线通常画成虚线.
小资料
如图,在一个任意的四边形ABCD内任取一点O,
连接AO,BO、CO、DO,
得到△OAB,△OBC,△OCD和△ODA.
这四个三角形所有内角之和为 4 × 180°,比四边形ABCD的内角和多出了以O为顶点的四个角之和,即360°.
从而,可以得出任意四边形的内角和等于:
4×180°-360°= 360°.
(4) 用上面的方法,你能求出任意五边形的内角和吗
(5) 如果O是n边形A1A2A3 ··· An-1An内的一点连接 OA1,OA2,···,OAn-1,OAn,
你能利用△OA1A2,△OA2A3,···,△OAn-1An,△OAnA1 的所有内角的度数之和,推导出n边形A1A2A3
··· An-1An 的内角和吗 与同学交流.
n边形的内角和等于(n- 2)·180°
观察与思考
你还记得什么是三角形的外角吗 三角形外角的意义可以推广到多边形上.
多边形一个角的一边与另一边的反向延长线所组成的角,叫做多边形的外角.
任意画出一个四边形ABCD.思考下面的问题:
(1) 从四边形ABCD的任意一个顶点 (例如顶点C)处,画四边形的外角.
你能画出几个 它们具有什么
位置关系和数量关系
(2) 四边形ABCD共有多少个外角
(3) 四边形ABCD的一个外角跟与它相邻的内角有什么数量关系
(4) 如图 ,在四边形ABCD的每个顶点处分别画出它的一个外角这些外角的和是多少 你是怎样得到这个结果的 五边形呢 六边形呢
四边形ABCD的每个外角都与相邻的内角组成一个平角.
四边形有4个内角,组成的四个平角的和是4×180°.
再减去四边形的内角和360°,因此这4个外角的和为360°.
一般地,在多边形的每个顶点处分别取多边形的一个外角, 这些外角的和叫做多边形的外角和.
多边形的外角和
如图所示,∠1, ∠2,∠3,∠4的和就是四边形ABCD的外角和四边形的外角和等于360°.
(5) n边形的外角和是多少 说明你的理由.
n边形的每一个内角跟与它相邻的一个外角都组成一个平角,n边形有n个内角,所以,这些平角的和为n·180°,其中所有内角的和为 (n-2)·180°,因此n边形的外角和为:
n·180°-(n - 2)·180°
= n·180°-n·180°+2×180°
=360°
多边形的外角和等于360°.
挑战自我
任意多边形的内角中,最多有几个锐角 说明理由.
由于n边形外角和为360°,则外角中至多有三个钝角,因此n边形内角中最多有三个锐角.
练 习
1. 分别计算九边形、十二边形、二十边形的内角和.
九边形的内角和为:(9-2) ×180°=1260°
十二边形的内角和为:(12-2) ×180°=1800°
二十边形的内角和为:(20-2) ×180°=3240°.
2. 求正八边形的每个内角与每个外角的度数.
每个内角为135°,每个外角为45°.
习题 13.2
复习与巩固
1. 把n边形内的任意一点与各顶点相连接,这些线段把n边形分成多少个三角形 把n边形一边上的任意一点(不是顶点)与其他边上的各顶点相连接,这些线段把n边形分成多少个三角形
把n边形内的任意一点与各顶点相连接这些线段把n边形分成(n-2)个三角形;
把n边形一边上的任意一点(不是顶点)与其他边上的各顶点相连接这些线段把n边形分成(n-1)个三角形.
2. 如果一个多边形从一个顶点出发的对角线把这个多边形分成6个三角形,这个多边形是几边形
设这个多边形的边数是n,
由题意得,n-2=6.
解答n=8.
答:这个多边形是八边形.
3.下面的说法正确吗 如果不正确,你能用一个例子作出说明吗
(1) 如果一个多边形的各边都相等,那么它是正多边形;
如果一个多边形的各边都相等,那么它是正多边形,说法错误,菱形的各边都相等,但菱形不是正多边形;
(2) 如果一个多边形的所有内角都相等,那么它是正多边形.
如果一个多边形的所有内角都相等,那么它是正多边形,说法错误,矩形的四个角都是直角但矩形不是正多边形.
4. 正三角形、正方形、正五边形、正六边形的一个内角各是多少度
根据多边形的内角和公式可得:
正三角形的内角和为: (3-2) ×180°=180°,
∴正三角形的每一个内角为180°÷3=60°
正方形的内角和为:(4-2) ×180°=360°,
∴正方形的每一个内角为360°÷4=90°;
正五边形的内角和为:(5-2) ×180°=540°,
∴正五边形的每一个内角为540°÷5=108°;
正六边形的内角和为:(6-2) ×180°=720°,
∴正六边形的每一个内角为720°÷6=120°.
5. 一个多边形的内角和为 2700°,求它的边数.
设这个多边形的边数为n.
由题意得:(n-2) ×180°=2700°
解得 n=17.
即这个多边形的边数为17.
6. 一个多边形的内角和与外角和相等,这个多边形是几边形
设这个多边形的边数为n.
由题意得:(n-2) ×180°=360°
解得n=4.
即这个多边形是四边形。
拓展与延伸
7. 如图,五角星中含有几个五边形 几个四边形 几个三角形 把它们分别表示出来.
略
8. 能不能找出一个多边形,使它的每一个内角都是与它相邻外角的3倍
能,这个多边形是正八边形.
每一个外角的度数:180°÷4=45°,
360÷45=8.
这个多边形是正八边形
探索与创新
9. (1) 四边形ABCD中,从顶点A引对角线AC,将四边形分为几个三角形 这几个三角形所有内角之和与四边形内角之和有什么关系
由图形可知,从顶点A引对角线AC,将四边形分成2个三角形,这2个三角形所有内角和等于四边形内角之和;
(2) 五边形ABCDE中,过顶点A最多能引几条对角线 它们将五边形分为几个三角形 这几个三角形所有内角之和与五边形内角之和有什么关系
五边形ABCDE中,从顶点A最多能引2条对角线,它们将五边形分成3个三角形,这3个三角形所有内角和等于五边形内角之和;
(3) 过n边形的任意一个顶点最多可引几条对角线 它们将n边形分为几个三角形这几个三角形所有内角之和与n边形内角之和有什么关系 由此你能得出n边形内角之和的公式吗 试一试.
过n边形的任意一个顶点最多可以 (n-3)条对角线,它们将n边形分为 (n-2) 个三角形,这(n-2)个三角形所有内角之和等于n边形内角之和,由此可得出n边形内角之和的公式为 (n-2)×180°
10. 四边形的边比三角形的边多了一条,内角和多了多少度 五边形的边比四边形的边多了一条,内角和多了多少度 由此可以推测,多边形的边每多一条,内角和多了多少度 说明你的理由.
四边形的边比三角形的边多了一条,内角和多了 360°-180°=180°,
五边形的边比四边形的边多了一条,内角和多了540°-360°=180°,
由此可以推测,多边形的边每多一条,内角和多了180°,
∵多边形的内角和为: (n-2)×180°.
∴若多边形边数每多一条,则它的内角和多了
(n+1-2) ×180°- (n-2) ×180=180°.
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
