初中数学青岛版 七年级下册13.3 圆课件(共60张PPT)
文档属性
| 名称 | 初中数学青岛版 七年级下册13.3 圆课件(共60张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 61.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 19:54:30 | ||
图片预览







文档简介
(共60张PPT)
第13章
平面图形的认识
青岛版 七年级下册
13 . 3
圆
观察与思考
(1) 在图中有许多的形象,你还能举出圆的几个实例吗
圆 桌
轮 胎
轴 承
(2) 你能说明用圆规画的道理吗 除了可以用圆规画圆之外,你还有其他画圆的方法吗 用你知道的方法画圆,体会圆是怎样画出来的.
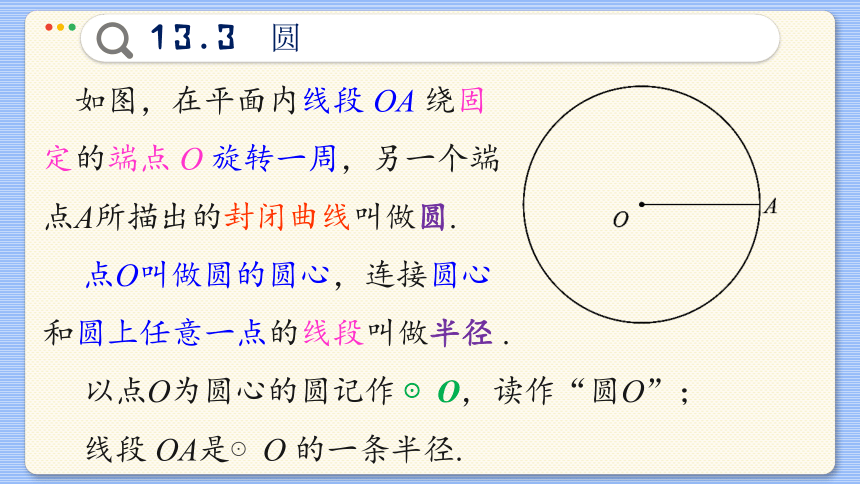
如图,在平面内线段 OA 绕固
定的端点 O 旋转一周,另一个端
点A所描出的封闭曲线叫做圆.
点O叫做圆的圆心,连接圆心
和圆上任意一点的线段叫做半径 .
以点O为圆心的圆记作 ⊙O,读作“圆O”;
线段 OA是⊙O 的一条半径.
(3) 一个圆有多少条半径 对于同一个圆来说,这些半径的长相等吗 为什么 与同学交流.
实验与探究
画一个半径为5厘米的⊙O,在⊙O上任意取A,B两点,连接OA,OB.
O
A
B
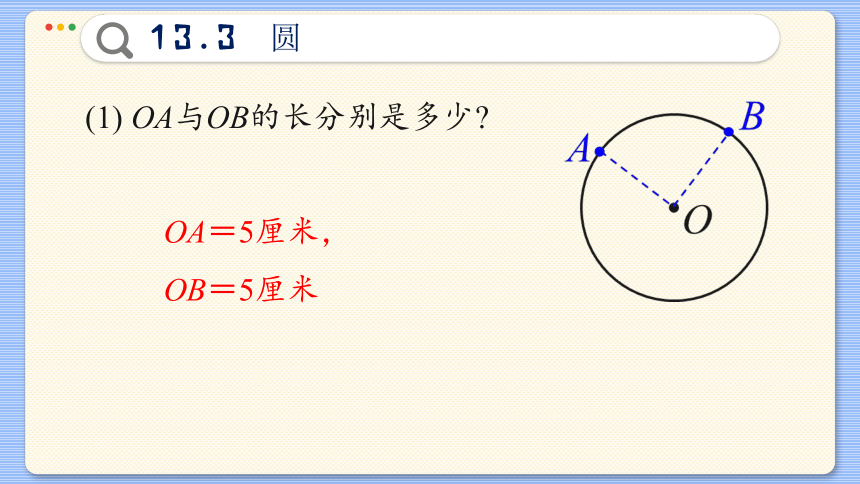
(1) OA与OB的长分别是多少
OA=5厘米,
OB=5厘米
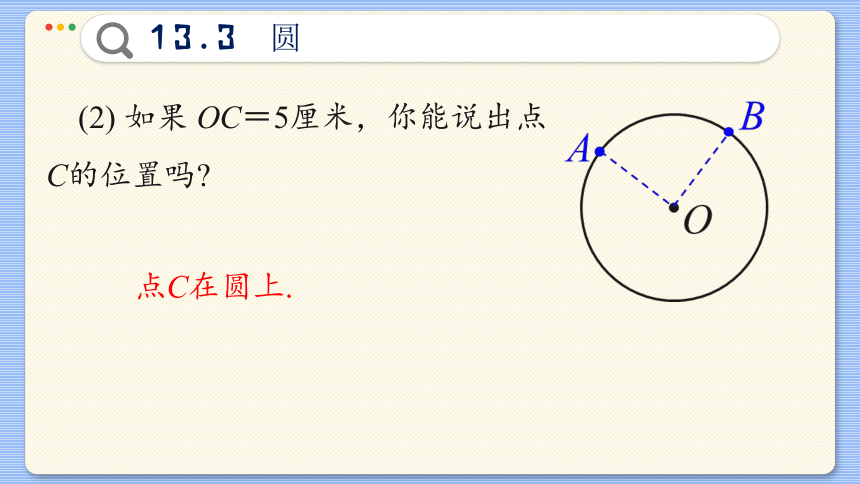
(2) 如果 OC=5厘米,你能说出点C的位置吗
点C在圆上.
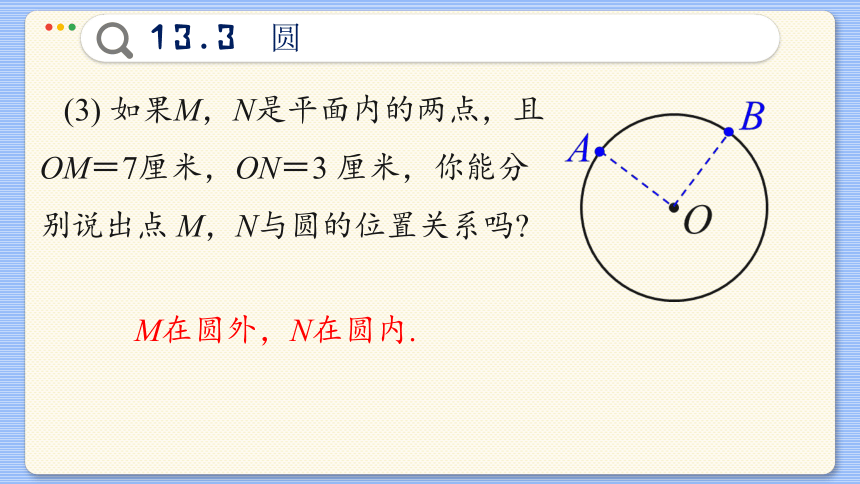
(3) 如果M,N是平面内的两点,且
OM=7厘米,ON=3 厘米,你能分
别说出点 M,N与圆的位置关系吗
M在圆外,N在圆内.
(4) 观察右图,平面内的点与圆有几种位置关系
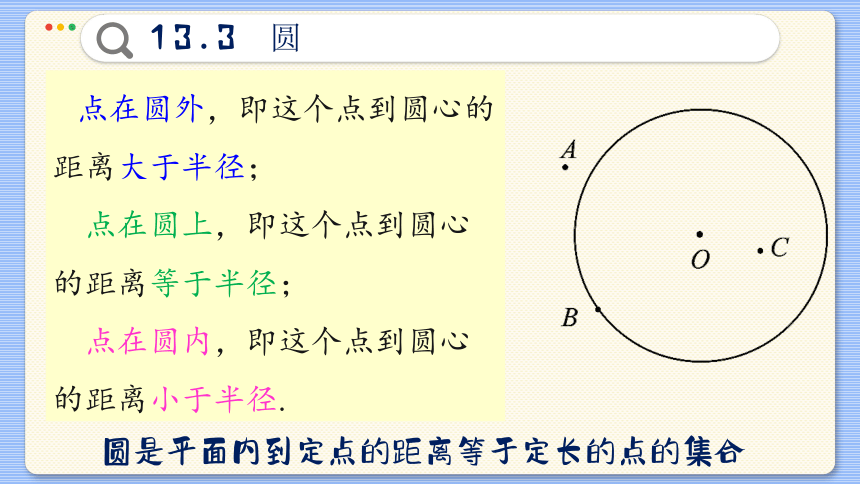
在平面内,点与圆的位置关系有三种:点在圆外、点在圆上、点在圆内.
例如图中,点A在圆外,点B在圆上,点C在圆内.
点在圆外,即这个点到圆心的距离大于半径;
点在圆上,即这个点到圆心的距离等于半径;
点在圆内,即这个点到圆心的距离小于半径.
圆是平面内到定点的距离等于定长的点的集合
(5) 你能用集合语言描述圆的内部和外部吗
①圆的内部是_____________________点的集合;
②圆的外部是_____________________点的集合.
到定点的距离小于定长
到定点的距离大于定长
(6) 在⊙O上任取两点,用线段连接它们,所得到的线段叫做弦.
再画出一条经过圆心 O 的弦,它与⊙O的半径有什么关系
经过圆心的弦叫做直径.
经过圆心O的弦是半径的2倍.
例如图中,
C,D是⊙O上的两点,线段 CD是⊙O的弦;
弦AB过圆心O,它是⊙O的一条直径.
由于OA,OB是⊙O的两条半径,
O是AB的中点,
因此在同一个圆中,直径等于半径的2倍.
一个圆有无数条直径.
圆上任意两点间的部分叫做圆弧,简称弧.
用符号“⌒”表示.
以C,D两点为端点的圆弧记作 ,读作“弧 CD”.
由于以C,D为端点的弧有两条,为了加以区别,有时也用三个字母表示弧.
例如,在图中, 与分别表示两条不同的弧.
圆的一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
例如,图中的是优弧,弧 是劣弧,扇形OCBD和扇形OCAD分别是由半径OC,OD与和半径OC,OD与组成的扇形.
练 习
1. 已知 ⊙O的半径为8厘米,A为平面内的一点. 当OA符合下列条件时,分别指出点A与⊙O的位置关系:
(1) OA=7.9厘米;
(2) OA=8厘米;
(3) OA = 8.01厘米.
点A在⊙O内;
点A在⊙O上;
点A在⊙O外;
2. (1) 圆的一条弦所对的弧有几条
(2) 在图中有几条弧 哪些是优弧
哪些是劣弧
圆的一条弦所对的弧有两条
图中有11条弧,半圆有两条,优孤有, ,,,劣弧有,,,,.
交流与发现
观察下图的两幅图片.
① 硬 币
② 环形靶
① 硬 币
(1) 图①中,同一币值的两枚硬币的边缘都是圆. 把其中
的一枚硬币放到另一枚硬币上,这两个圆能重合吗
能
能够重合的圆叫做等圆.
如图, ⊙O1和⊙O2是等圆.
② 环形靶
(2) 图②是一个练习射击用的环形靶,它是由若干个圆组
成的. 这些圆的圆心和半径有什么特点 与同学交流.
圆心相同,半径不等;
圆心相同、半径不等的圆叫做同心圆.
如图,r1> r2,半径分别是 r1和r2的两个圆都以点O为圆心,它们是同心圆.
(3) 用圆规分别画出两个等圆和两个同心圆.
画等圆和画同心圆有什么不同
等圆的半径相等,只是圆心的位置不同.
(4) 你见过国际奥委会的会徽吗 会徽上的五个圆是等圆吗 你还能举出生活中等圆的实例吗
是;
一个圆柱的上下两个底面
(答案不唯一)
例 1
两个同心圆之间的部分叫做圆环.如果圆环中大圆的半径为下,小圆的半径为 ,求圆环的面积.
圆环的面积等于大圆面积与小圆面积的差,所求圆环的面积为
πr2- π()2 =πr2
例 2
(1) 用长度分别为1米和2米的两根绳子围成两个同心圆,这两个圆半径之差是多少
1米长的绳子围成的圆的半径为米,2米长的绳子围成的圆的半径为米. 所以,两个同心圆的半径之差为
-= ≈ 0.159(米)
(2) 把地球的赤道近似地看做一个圆.如果环绕地球赤道有一个圆,它的周长比赤道的周长多1米,这两个同心圆半径之差是多少 想想看,两圆之间能伸进你的拳头吗
设地球的半径为r,因为赤道与环绕赤道的圆是两个同心圆,所以这两个圆半径之差为
- r =( r + ) - r = ≈0.159 (米).
一个成年人的拳头高约8厘米,所以两圆之间能伸进一个人的拳头.
挑战自我
(1) 如图,将一枚半径为r的硬币沿一条直线从点M 出发,滚动一周,到达点N.线段MN的长是多少 硬币的圆心走过的路程是多少
MN=2πr
答:线段MN的长是2πr,硬币的圆心走过的路程是2πr.
(2) 如图,取两枚半径都为r的硬币A,B,平放到桌面上,将硬币A固定,硬币B从硬币A的边缘上的一点M出发,沿硬币A的边缘滚动一周.回到原来的位置.硬币B的圆心走过的路程是多少 在滚动时硬币B转了几周
硬币B的圆心走过的路程是以A为圆心,
以2r为半径的圆的周长,
即2π×2r=4πr
因为硬币A的周长是2πr,
所以在滚动时硬币B转了2周.
练 习
1. 你能用图形表示“平面内到点 A的距离大于2厘米而小于3 厘米的点的集合”吗
分别以A为圆心,以2厘米和3厘米为半径画圆,圆环部分即为所求 (不包括圆上的点).
A
2. 如果 A的周长是⊙B的周长的4倍,那么⊙A的面积是⊙B 的面积的几倍
习题 13.3
复习与巩固
1. 在△ABC中,AB=3厘米,BC=4厘米,CA=5厘米.
(1) 以点A为圆心,以3厘米长为半径画圆,确定点 B,C与⊙A的位置关系;
因为AB=3厘米=半径,AC=5厘米>半径1
所以以点A为圆心,以3厘米长为半径画圆时,点B在圆上,点C在圆外.
(2) 以点A为圆心,以4厘米长为半径画圆,确定点 B,C与⊙A的位置关系;
因为AB=3厘米<半径,AC=5厘米>半径
所以以点A为圆心,以4厘米长为半径画圆时,点B在圆内,点C在圆外.
(3) 以点B为圆心,以4厘米长为半径画圆,确定点 A,C与⊙B的位置关系;
因为 AB=3厘米<半径,
BC=4厘米=半径
所以以点B为圆心,以4厘米长为半径画圆时,点A在圆内,点C在圆上.
2. 早在2 000多年前的战国时期,《墨经》一书中就给出了圆的描述性定义:“圈(这里读yun),一中同长也.”这就是说,圆是平面内到定点的距离等于定长的点的集合. 其中,定点是_____________,定长是___________.
圆心
半径
3. A,B两点的距离为4厘米. 用图形表示具有下列 性质的点的集合,并指出它们是怎样的图形:
(1) 到点A的距离等于3厘米的点的集合;
(2) 到点B的距离等于3 厘米的点的集合;
(3) 到A,B两点的距离都等于3厘米的点的集合;
点C、D即为符合条件的点的集合
(4) 到A,B两点的距离都不大于3 厘米的点的集合.
图中阴影部分即为符合条件的点的集合(含边界)
4. 以一个定点为圆心,可以画_____个圆,它们是_______;以一条已知线段为半径画圆,可以画_____个圆,它们是______;以一个定点为圆心,以一条已知线段为半径,可以画_____个圆.
无数
同心圆
无数
等圆
一
5. (1) 已知圆的周长为4π,求它的面积;
因为圆的周长为4,
所以此圆的半径为=2,
所以圆的面积为π× 22 = 4π;
(2) 已知圆的周长为c,求它的面积.
因为圆的周长为c,
所以此圆的半径为 ,
所以圆的面积为 π×() 2=.
6. 在半径为R的圆形工件中截去一个圆孔,剩余面积是
圆孔面积的3倍,求圆孔的半径.
拓展与延伸
7. 如图,正方形的边长为2,分别以正方形的两个相对顶点为圆心,以正方形的一边为半径画弧.求蓝色图形的面积.
8. 小亮家距学校10千米,小莹家距小亮家3 千米.
(1) 如果小亮家、小莹家、学校在同一条直线上,那么
小莹家距学校多少千米
当小莹家在小亮家与学校之间时,小莹家距学校10 - 3 = 7千米;
当小亮家在小莹家与学校之间时,小莹家距学校10 + 3 = 13千米.
故小莹家距学校13千米或7千米.
(2) 如果小亮家、小莹家、学校在同一平面内,那么小
莹家与学校的距离在什么范围内 你能画一个图形
表示出来吗
小莹家在以小亮家为圆心,3千米为半径的圆上,设小莹家离学校的距离为d,则 (10 - 3) <d<(10+3) ,
解得: 7千米<d<13千米,
如图所示:
探索与创新
9. 在同一个圆中,画出一条直径与任意一条不过圆心的弦,比较它们的长短,你会得到什么结论 请说明理由.
本课结束!
第13章
平面图形的认识
青岛版 七年级下册
13 . 3
圆
观察与思考
(1) 在图中有许多的形象,你还能举出圆的几个实例吗
圆 桌
轮 胎
轴 承
(2) 你能说明用圆规画的道理吗 除了可以用圆规画圆之外,你还有其他画圆的方法吗 用你知道的方法画圆,体会圆是怎样画出来的.
如图,在平面内线段 OA 绕固
定的端点 O 旋转一周,另一个端
点A所描出的封闭曲线叫做圆.
点O叫做圆的圆心,连接圆心
和圆上任意一点的线段叫做半径 .
以点O为圆心的圆记作 ⊙O,读作“圆O”;
线段 OA是⊙O 的一条半径.
(3) 一个圆有多少条半径 对于同一个圆来说,这些半径的长相等吗 为什么 与同学交流.
实验与探究
画一个半径为5厘米的⊙O,在⊙O上任意取A,B两点,连接OA,OB.
O
A
B
(1) OA与OB的长分别是多少
OA=5厘米,
OB=5厘米
(2) 如果 OC=5厘米,你能说出点C的位置吗
点C在圆上.
(3) 如果M,N是平面内的两点,且
OM=7厘米,ON=3 厘米,你能分
别说出点 M,N与圆的位置关系吗
M在圆外,N在圆内.
(4) 观察右图,平面内的点与圆有几种位置关系
在平面内,点与圆的位置关系有三种:点在圆外、点在圆上、点在圆内.
例如图中,点A在圆外,点B在圆上,点C在圆内.
点在圆外,即这个点到圆心的距离大于半径;
点在圆上,即这个点到圆心的距离等于半径;
点在圆内,即这个点到圆心的距离小于半径.
圆是平面内到定点的距离等于定长的点的集合
(5) 你能用集合语言描述圆的内部和外部吗
①圆的内部是_____________________点的集合;
②圆的外部是_____________________点的集合.
到定点的距离小于定长
到定点的距离大于定长
(6) 在⊙O上任取两点,用线段连接它们,所得到的线段叫做弦.
再画出一条经过圆心 O 的弦,它与⊙O的半径有什么关系
经过圆心的弦叫做直径.
经过圆心O的弦是半径的2倍.
例如图中,
C,D是⊙O上的两点,线段 CD是⊙O的弦;
弦AB过圆心O,它是⊙O的一条直径.
由于OA,OB是⊙O的两条半径,
O是AB的中点,
因此在同一个圆中,直径等于半径的2倍.
一个圆有无数条直径.
圆上任意两点间的部分叫做圆弧,简称弧.
用符号“⌒”表示.
以C,D两点为端点的圆弧记作 ,读作“弧 CD”.
由于以C,D为端点的弧有两条,为了加以区别,有时也用三个字母表示弧.
例如,在图中, 与分别表示两条不同的弧.
圆的一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
例如,图中的是优弧,弧 是劣弧,扇形OCBD和扇形OCAD分别是由半径OC,OD与和半径OC,OD与组成的扇形.
练 习
1. 已知 ⊙O的半径为8厘米,A为平面内的一点. 当OA符合下列条件时,分别指出点A与⊙O的位置关系:
(1) OA=7.9厘米;
(2) OA=8厘米;
(3) OA = 8.01厘米.
点A在⊙O内;
点A在⊙O上;
点A在⊙O外;
2. (1) 圆的一条弦所对的弧有几条
(2) 在图中有几条弧 哪些是优弧
哪些是劣弧
圆的一条弦所对的弧有两条
图中有11条弧,半圆有两条,优孤有, ,,,劣弧有,,,,.
交流与发现
观察下图的两幅图片.
① 硬 币
② 环形靶
① 硬 币
(1) 图①中,同一币值的两枚硬币的边缘都是圆. 把其中
的一枚硬币放到另一枚硬币上,这两个圆能重合吗
能
能够重合的圆叫做等圆.
如图, ⊙O1和⊙O2是等圆.
② 环形靶
(2) 图②是一个练习射击用的环形靶,它是由若干个圆组
成的. 这些圆的圆心和半径有什么特点 与同学交流.
圆心相同,半径不等;
圆心相同、半径不等的圆叫做同心圆.
如图,r1> r2,半径分别是 r1和r2的两个圆都以点O为圆心,它们是同心圆.
(3) 用圆规分别画出两个等圆和两个同心圆.
画等圆和画同心圆有什么不同
等圆的半径相等,只是圆心的位置不同.
(4) 你见过国际奥委会的会徽吗 会徽上的五个圆是等圆吗 你还能举出生活中等圆的实例吗
是;
一个圆柱的上下两个底面
(答案不唯一)
例 1
两个同心圆之间的部分叫做圆环.如果圆环中大圆的半径为下,小圆的半径为 ,求圆环的面积.
圆环的面积等于大圆面积与小圆面积的差,所求圆环的面积为
πr2- π()2 =πr2
例 2
(1) 用长度分别为1米和2米的两根绳子围成两个同心圆,这两个圆半径之差是多少
1米长的绳子围成的圆的半径为米,2米长的绳子围成的圆的半径为米. 所以,两个同心圆的半径之差为
-= ≈ 0.159(米)
(2) 把地球的赤道近似地看做一个圆.如果环绕地球赤道有一个圆,它的周长比赤道的周长多1米,这两个同心圆半径之差是多少 想想看,两圆之间能伸进你的拳头吗
设地球的半径为r,因为赤道与环绕赤道的圆是两个同心圆,所以这两个圆半径之差为
- r =( r + ) - r = ≈0.159 (米).
一个成年人的拳头高约8厘米,所以两圆之间能伸进一个人的拳头.
挑战自我
(1) 如图,将一枚半径为r的硬币沿一条直线从点M 出发,滚动一周,到达点N.线段MN的长是多少 硬币的圆心走过的路程是多少
MN=2πr
答:线段MN的长是2πr,硬币的圆心走过的路程是2πr.
(2) 如图,取两枚半径都为r的硬币A,B,平放到桌面上,将硬币A固定,硬币B从硬币A的边缘上的一点M出发,沿硬币A的边缘滚动一周.回到原来的位置.硬币B的圆心走过的路程是多少 在滚动时硬币B转了几周
硬币B的圆心走过的路程是以A为圆心,
以2r为半径的圆的周长,
即2π×2r=4πr
因为硬币A的周长是2πr,
所以在滚动时硬币B转了2周.
练 习
1. 你能用图形表示“平面内到点 A的距离大于2厘米而小于3 厘米的点的集合”吗
分别以A为圆心,以2厘米和3厘米为半径画圆,圆环部分即为所求 (不包括圆上的点).
A
2. 如果 A的周长是⊙B的周长的4倍,那么⊙A的面积是⊙B 的面积的几倍
习题 13.3
复习与巩固
1. 在△ABC中,AB=3厘米,BC=4厘米,CA=5厘米.
(1) 以点A为圆心,以3厘米长为半径画圆,确定点 B,C与⊙A的位置关系;
因为AB=3厘米=半径,AC=5厘米>半径1
所以以点A为圆心,以3厘米长为半径画圆时,点B在圆上,点C在圆外.
(2) 以点A为圆心,以4厘米长为半径画圆,确定点 B,C与⊙A的位置关系;
因为AB=3厘米<半径,AC=5厘米>半径
所以以点A为圆心,以4厘米长为半径画圆时,点B在圆内,点C在圆外.
(3) 以点B为圆心,以4厘米长为半径画圆,确定点 A,C与⊙B的位置关系;
因为 AB=3厘米<半径,
BC=4厘米=半径
所以以点B为圆心,以4厘米长为半径画圆时,点A在圆内,点C在圆上.
2. 早在2 000多年前的战国时期,《墨经》一书中就给出了圆的描述性定义:“圈(这里读yun),一中同长也.”这就是说,圆是平面内到定点的距离等于定长的点的集合. 其中,定点是_____________,定长是___________.
圆心
半径
3. A,B两点的距离为4厘米. 用图形表示具有下列 性质的点的集合,并指出它们是怎样的图形:
(1) 到点A的距离等于3厘米的点的集合;
(2) 到点B的距离等于3 厘米的点的集合;
(3) 到A,B两点的距离都等于3厘米的点的集合;
点C、D即为符合条件的点的集合
(4) 到A,B两点的距离都不大于3 厘米的点的集合.
图中阴影部分即为符合条件的点的集合(含边界)
4. 以一个定点为圆心,可以画_____个圆,它们是_______;以一条已知线段为半径画圆,可以画_____个圆,它们是______;以一个定点为圆心,以一条已知线段为半径,可以画_____个圆.
无数
同心圆
无数
等圆
一
5. (1) 已知圆的周长为4π,求它的面积;
因为圆的周长为4,
所以此圆的半径为=2,
所以圆的面积为π× 22 = 4π;
(2) 已知圆的周长为c,求它的面积.
因为圆的周长为c,
所以此圆的半径为 ,
所以圆的面积为 π×() 2=.
6. 在半径为R的圆形工件中截去一个圆孔,剩余面积是
圆孔面积的3倍,求圆孔的半径.
拓展与延伸
7. 如图,正方形的边长为2,分别以正方形的两个相对顶点为圆心,以正方形的一边为半径画弧.求蓝色图形的面积.
8. 小亮家距学校10千米,小莹家距小亮家3 千米.
(1) 如果小亮家、小莹家、学校在同一条直线上,那么
小莹家距学校多少千米
当小莹家在小亮家与学校之间时,小莹家距学校10 - 3 = 7千米;
当小亮家在小莹家与学校之间时,小莹家距学校10 + 3 = 13千米.
故小莹家距学校13千米或7千米.
(2) 如果小亮家、小莹家、学校在同一平面内,那么小
莹家与学校的距离在什么范围内 你能画一个图形
表示出来吗
小莹家在以小亮家为圆心,3千米为半径的圆上,设小莹家离学校的距离为d,则 (10 - 3) <d<(10+3) ,
解得: 7千米<d<13千米,
如图所示:
探索与创新
9. 在同一个圆中,画出一条直径与任意一条不过圆心的弦,比较它们的长短,你会得到什么结论 请说明理由.
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
