第14章 位置与坐标 回顾与复习-初中数学青岛版 七年级下册 同步课件(共43张PPT)
文档属性
| 名称 | 第14章 位置与坐标 回顾与复习-初中数学青岛版 七年级下册 同步课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 57.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 20:17:27 | ||
图片预览










文档简介
(共43张PPT)
第14章 位置与坐标
青岛版 七年级下册
第14章
回顾与总结
回顾与总结
1. 如何用有序数对表示平面内点的位置
2. 什么是平面直角坐标系 在直角坐标系中,如何根据
坐标描出点的位置 如何由点的位置写出它的坐标
3. 直角坐标系将平面分为几部分 各部分的名称分别是什么 各部分点的坐标有什么特征 坐标轴上点的坐标有什么特征
4. 如何利用坐标描述一个简单的图形
5.你体会到直角坐标系对于建立数与图形之间的联系有怎样的作用
6.怎样用方向和距离描述平面内两个物体的相对位置 试举例说明.
综合练习
复习与巩固
1. 指出下列各点的横坐标和纵坐标,并按所在象限将
它们进行分类:
A(4,2),B(-2,2),C(3,1),D(-1,-3),
E(-2,1),F(-2,-2),G(2,3),H(4,-1).
∵ A(4,2),B(-2,2),C(3,1),
D(-1,-3),E(-2,1),
F(-2,-2),G(2,3),
H(4,-1).
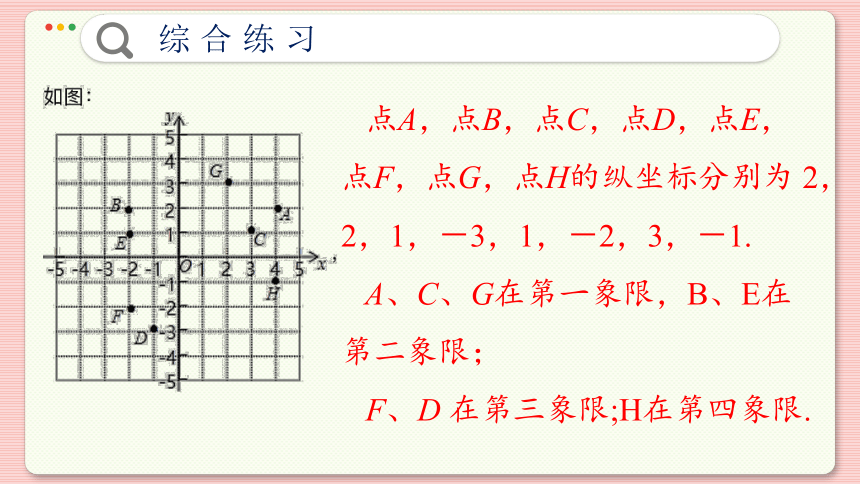
∴ 点A,点B,点C,点D,点E,点F,点G,点H的横坐标分别为4,-2,3,-1,-2,2,2,4;
点A,点B,点C,点D,点E,点F,点G,点H的纵坐标分别为 2,2,1,-3,1,-2,3,-1.
A、C、G在第一象限,B、E在第二象限;
F、D 在第三象限;H在第四象限.
2. 在直角坐标系中描出下列各点,分别将各组中的点顺次连接起来,得到怎样的图形
(1) (-1,-2),(-1,2),(1,2),(1,-2),
(-1,-2);
(2) (1,0),(2,2),(3,0),(2,-2),(1,0).
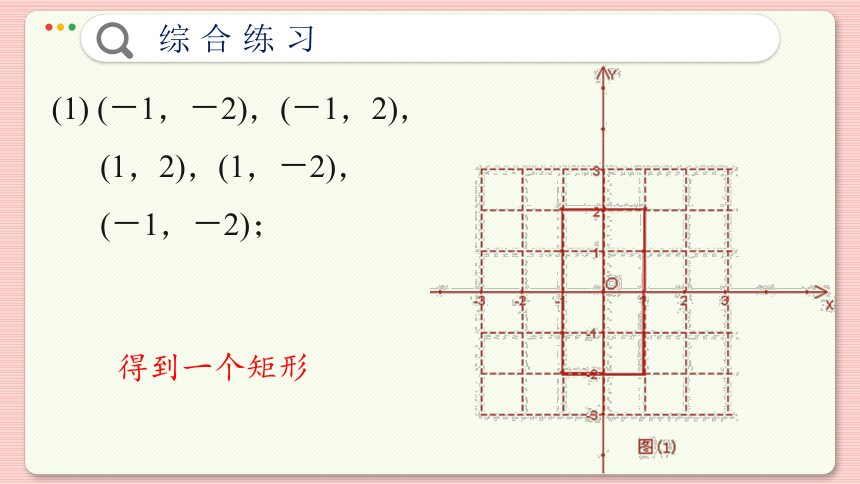
(1) (-1,-2),(-1,2),
(1,2),(1,-2),
(-1,-2);
得到一个矩形
(2) (1,0),(2,2),(3,0),
(2,-2),(1,0).
得到一个菱形
3.如图,请用两种不同的方式建立直角坐标系,并用坐标表示图形中各顶点的位置.
第一种如图所示:
各顶点分别为A、B、C、D、E、F,坐标分别为(0,6.5),(3.5,6.5),(3.5,3.5),(8.5,3.5),(8.5,0),(0,0)
第二种如图所示:
各顶点分别为A、B、C、D、E、F,坐标分别为(-3.5,3),(0,3),(0,0),(5,0),(5,-3.5),
(-3.5,-3.5).
4. 在直角坐标系中,任意选定A,B两点,找出分别以A,
B的横坐标的平均数为横坐标、以 A,B 的纵坐标的
平均数为纵坐标的点 C.你发现A,B,C三点的位置有
什么关系
设点A的坐标为 (a,m),点B的坐标为 (b,n),
则点C的坐标为(,),
5. 填空:
(1) 如果点(a,-b)在第一象限,那么a___0,b___0
(填“>”或“<”);
(2) 如果点(a,b)在第一象限,那么点 (-b,a) 在第
____象限;
>
<
二
(3) 如果点(a,b)在第二象限,那么点 (b,-a) 在第
______象限;
(4) 如果点 (a,b)在第四象限,那么点 (-b,-a)在第
______象限
一
四
6. 如图,⊙O的半径 r=4,圆心O在直角坐标系的原点,⊙O与坐标轴分别交于点A,B,C,D.写出A,B,C,D各点的坐标.
根据题意可知OA=OB=OC=OD=4,
故点A、B、C、D的坐标分别为:(4,0)、(0,4)、(-4,0)、(0,-4).
7. 如图,要在一个尺寸为80厘米×40厘米的长方形木板ABCD上钻一个圆孔,圆孔的圆心为P,点P到AD的距离为30厘米,到AB的距离为15厘米.建立适当的坐标系,以 10厘米为单位长度,分别写出圆心P及A,B,C,D各点的坐标.
根据题意作出图形如图所示:那么点圆心P及A,B,C,D 各点的坐标分别是(-1,-0.5),(-4,-2),(4,-2),(4,2),(-4,2)
8. 学校位于小亮家北偏东 30°方向,距离为300 米;学校位于大刚家南偏东45°方向距离为400米.用刻度尺和量角器,选择适当的比例尺画出学校和他们两人的家的位置,并分别求出大刚家相对于小亮家的位置和小亮家相对于大刚家的位置.
如图所示:大刚家位于小亮家的位置北偏西20°方向,距离为580米;大亮家位于小刚家的位置南偏东20°方向,距离为580米.
拓展与延伸
9. 如图是某县的地图 (局部),每个小方格的边长表示3公里.
(1) 借助刻度尺和量角器,描述各镇相对于城关镇的位置.如果以 C镇为参照点呢
以城关镇为原点,
A镇在城关镇东北方向,
B镇在城关镇西南方向,
C镇在城关镇正东方向,
D镇在城关镇东南方向;
(1) 借助刻度尺和量角器,描述各镇相对于城关镇的位置.如果以 C镇为参照点呢
以C镇为原点,
A镇在C镇西北方向,
B镇在C镇西南方向,
城关镇在C镇正西方向,
D镇在C镇正南方向.
(2) 分别以城关镇和 C镇为坐标原点建立直角坐标系,写出各城镇的坐标.
以城关镇为原点,
A镇(5,5),
B镇(-2,-3),
C镇(10,0),
D镇(10,-4);
(2) 分别以城关镇和 C镇为坐标原点建立直角坐标系,写出各城镇的坐标.
以C镇为原点,
A镇(-5,5),
B镇(-12,-2),
城关镇(-10,0),
D镇(0,-4).
10. 在直角坐标系中,有 A (-2,3),B (2,-3),
C(2,3),D(-2,-3)四个点.
根据题意可得A点在二象限,B点在第四象限,C点在第一象限,D点在第三象限,点F在第二象限.
(1) 哪个点与点F(-3,4)
连接的线段与x轴、y
轴都不相交
点F与点A的连线不与x、y轴的相交;
(2) 哪个点与点F连接的
线段只与x轴相交,而
不与y轴相交
点F与点D的连线只与x轴相交,而不与y轴相交点;
(3) 哪个点与点F连接的线
段与x轴和y轴都相交
点F与点B的连线与x轴和y轴都相交.
探索与创新
11. 俄国著名作家列夫·托尔斯泰在他的作品中写过一个故事:一个叫巴赫姆的人到草原上购置土地. 卖地的人提出一个奇怪的条件:只要有人肯出1000卢布(俄国货币),从日出到日落买地人走过的路线所围成的土地都归他.但是,如果日落之前回不到原来的出发点,不但得不
到土地,也不退回1000卢布.贪心的巴赫姆付钱后从一大早就开始他的圈地旅行.他先向正东方向走了 10俄里 (1俄里1.067千米),再朝正北方向走了 12.7俄里,又朝正西方向走了2俄里. 这时,他发现天色不早,就向着出发点直奔而去,终于在日落时跑回出发点,但一头栽在地上,再也没有醒过来.
(1) 请你选择适当的比例尺,画出巴赫姆走过的路线;
巴赫姆走过的路线:
A→B→C→D→A.
(2) 当他发现天色不早时,出发点在他的什么方向 距离出发地有多远(精确到0.1俄里)
作DH⊥AB于H
在Rt△AHD中
AH=AB-BH=10-2=8(俄里),
DH=BC=12.7(俄里).
∴ AD==≈15.0(俄里)
tan∠ADH= ≈0.6299,
∴∠ADH≈32.2°,
∴出发点在他的南偏西32.2°方向上,距离出发地有15.0俄里.
12. 如果需要在电话中向一个同学说明如图所示的图形,你将怎样描述才能让他听明白
如图所示:
先画一个长×宽为7×9的长方形,再在它的右上角剪去一个长×宽为5×3的长方形,剩下的图形就是.
13. 在直角坐标系中,下面各点按顺序依次排列:
(0,1),(1,0), (0,-1), (0,2),(2,0),
(0, -2),(0,3),(3,0),(0,-3),···
(1) 这列点中的第1000个点的坐标是什么
观察各点规律发现:第1、4、7、10个点在y轴正半轴上,坐标分别(0,1),(0,2),(0,3),(0,4)···,
第2、5、8个点在x轴正半轴上,坐标分别 (1,0),
(2,0),(3,0),...,
第3、6、9 个点在y轴负半轴上,坐标分别(0, -1),(0,2),(0, - 3),···,
∵1000÷3 = 333余1,
∴第1000个点在y轴正半轴上,坐标为(0,334).
(2) (0,2012)是这列点中的第几个点
根据(1)的规律知点 (0,2012)在y轴正半轴上,
设它是第n个点,则 +1 = 2012,
解得:n=6034.
所以(0,2012) 是这列点中的第6034个点.
本课结束!
第14章 位置与坐标
青岛版 七年级下册
第14章
回顾与总结
回顾与总结
1. 如何用有序数对表示平面内点的位置
2. 什么是平面直角坐标系 在直角坐标系中,如何根据
坐标描出点的位置 如何由点的位置写出它的坐标
3. 直角坐标系将平面分为几部分 各部分的名称分别是什么 各部分点的坐标有什么特征 坐标轴上点的坐标有什么特征
4. 如何利用坐标描述一个简单的图形
5.你体会到直角坐标系对于建立数与图形之间的联系有怎样的作用
6.怎样用方向和距离描述平面内两个物体的相对位置 试举例说明.
综合练习
复习与巩固
1. 指出下列各点的横坐标和纵坐标,并按所在象限将
它们进行分类:
A(4,2),B(-2,2),C(3,1),D(-1,-3),
E(-2,1),F(-2,-2),G(2,3),H(4,-1).
∵ A(4,2),B(-2,2),C(3,1),
D(-1,-3),E(-2,1),
F(-2,-2),G(2,3),
H(4,-1).
∴ 点A,点B,点C,点D,点E,点F,点G,点H的横坐标分别为4,-2,3,-1,-2,2,2,4;
点A,点B,点C,点D,点E,点F,点G,点H的纵坐标分别为 2,2,1,-3,1,-2,3,-1.
A、C、G在第一象限,B、E在第二象限;
F、D 在第三象限;H在第四象限.
2. 在直角坐标系中描出下列各点,分别将各组中的点顺次连接起来,得到怎样的图形
(1) (-1,-2),(-1,2),(1,2),(1,-2),
(-1,-2);
(2) (1,0),(2,2),(3,0),(2,-2),(1,0).
(1) (-1,-2),(-1,2),
(1,2),(1,-2),
(-1,-2);
得到一个矩形
(2) (1,0),(2,2),(3,0),
(2,-2),(1,0).
得到一个菱形
3.如图,请用两种不同的方式建立直角坐标系,并用坐标表示图形中各顶点的位置.
第一种如图所示:
各顶点分别为A、B、C、D、E、F,坐标分别为(0,6.5),(3.5,6.5),(3.5,3.5),(8.5,3.5),(8.5,0),(0,0)
第二种如图所示:
各顶点分别为A、B、C、D、E、F,坐标分别为(-3.5,3),(0,3),(0,0),(5,0),(5,-3.5),
(-3.5,-3.5).
4. 在直角坐标系中,任意选定A,B两点,找出分别以A,
B的横坐标的平均数为横坐标、以 A,B 的纵坐标的
平均数为纵坐标的点 C.你发现A,B,C三点的位置有
什么关系
设点A的坐标为 (a,m),点B的坐标为 (b,n),
则点C的坐标为(,),
5. 填空:
(1) 如果点(a,-b)在第一象限,那么a___0,b___0
(填“>”或“<”);
(2) 如果点(a,b)在第一象限,那么点 (-b,a) 在第
____象限;
>
<
二
(3) 如果点(a,b)在第二象限,那么点 (b,-a) 在第
______象限;
(4) 如果点 (a,b)在第四象限,那么点 (-b,-a)在第
______象限
一
四
6. 如图,⊙O的半径 r=4,圆心O在直角坐标系的原点,⊙O与坐标轴分别交于点A,B,C,D.写出A,B,C,D各点的坐标.
根据题意可知OA=OB=OC=OD=4,
故点A、B、C、D的坐标分别为:(4,0)、(0,4)、(-4,0)、(0,-4).
7. 如图,要在一个尺寸为80厘米×40厘米的长方形木板ABCD上钻一个圆孔,圆孔的圆心为P,点P到AD的距离为30厘米,到AB的距离为15厘米.建立适当的坐标系,以 10厘米为单位长度,分别写出圆心P及A,B,C,D各点的坐标.
根据题意作出图形如图所示:那么点圆心P及A,B,C,D 各点的坐标分别是(-1,-0.5),(-4,-2),(4,-2),(4,2),(-4,2)
8. 学校位于小亮家北偏东 30°方向,距离为300 米;学校位于大刚家南偏东45°方向距离为400米.用刻度尺和量角器,选择适当的比例尺画出学校和他们两人的家的位置,并分别求出大刚家相对于小亮家的位置和小亮家相对于大刚家的位置.
如图所示:大刚家位于小亮家的位置北偏西20°方向,距离为580米;大亮家位于小刚家的位置南偏东20°方向,距离为580米.
拓展与延伸
9. 如图是某县的地图 (局部),每个小方格的边长表示3公里.
(1) 借助刻度尺和量角器,描述各镇相对于城关镇的位置.如果以 C镇为参照点呢
以城关镇为原点,
A镇在城关镇东北方向,
B镇在城关镇西南方向,
C镇在城关镇正东方向,
D镇在城关镇东南方向;
(1) 借助刻度尺和量角器,描述各镇相对于城关镇的位置.如果以 C镇为参照点呢
以C镇为原点,
A镇在C镇西北方向,
B镇在C镇西南方向,
城关镇在C镇正西方向,
D镇在C镇正南方向.
(2) 分别以城关镇和 C镇为坐标原点建立直角坐标系,写出各城镇的坐标.
以城关镇为原点,
A镇(5,5),
B镇(-2,-3),
C镇(10,0),
D镇(10,-4);
(2) 分别以城关镇和 C镇为坐标原点建立直角坐标系,写出各城镇的坐标.
以C镇为原点,
A镇(-5,5),
B镇(-12,-2),
城关镇(-10,0),
D镇(0,-4).
10. 在直角坐标系中,有 A (-2,3),B (2,-3),
C(2,3),D(-2,-3)四个点.
根据题意可得A点在二象限,B点在第四象限,C点在第一象限,D点在第三象限,点F在第二象限.
(1) 哪个点与点F(-3,4)
连接的线段与x轴、y
轴都不相交
点F与点A的连线不与x、y轴的相交;
(2) 哪个点与点F连接的
线段只与x轴相交,而
不与y轴相交
点F与点D的连线只与x轴相交,而不与y轴相交点;
(3) 哪个点与点F连接的线
段与x轴和y轴都相交
点F与点B的连线与x轴和y轴都相交.
探索与创新
11. 俄国著名作家列夫·托尔斯泰在他的作品中写过一个故事:一个叫巴赫姆的人到草原上购置土地. 卖地的人提出一个奇怪的条件:只要有人肯出1000卢布(俄国货币),从日出到日落买地人走过的路线所围成的土地都归他.但是,如果日落之前回不到原来的出发点,不但得不
到土地,也不退回1000卢布.贪心的巴赫姆付钱后从一大早就开始他的圈地旅行.他先向正东方向走了 10俄里 (1俄里1.067千米),再朝正北方向走了 12.7俄里,又朝正西方向走了2俄里. 这时,他发现天色不早,就向着出发点直奔而去,终于在日落时跑回出发点,但一头栽在地上,再也没有醒过来.
(1) 请你选择适当的比例尺,画出巴赫姆走过的路线;
巴赫姆走过的路线:
A→B→C→D→A.
(2) 当他发现天色不早时,出发点在他的什么方向 距离出发地有多远(精确到0.1俄里)
作DH⊥AB于H
在Rt△AHD中
AH=AB-BH=10-2=8(俄里),
DH=BC=12.7(俄里).
∴ AD==≈15.0(俄里)
tan∠ADH= ≈0.6299,
∴∠ADH≈32.2°,
∴出发点在他的南偏西32.2°方向上,距离出发地有15.0俄里.
12. 如果需要在电话中向一个同学说明如图所示的图形,你将怎样描述才能让他听明白
如图所示:
先画一个长×宽为7×9的长方形,再在它的右上角剪去一个长×宽为5×3的长方形,剩下的图形就是.
13. 在直角坐标系中,下面各点按顺序依次排列:
(0,1),(1,0), (0,-1), (0,2),(2,0),
(0, -2),(0,3),(3,0),(0,-3),···
(1) 这列点中的第1000个点的坐标是什么
观察各点规律发现:第1、4、7、10个点在y轴正半轴上,坐标分别(0,1),(0,2),(0,3),(0,4)···,
第2、5、8个点在x轴正半轴上,坐标分别 (1,0),
(2,0),(3,0),...,
第3、6、9 个点在y轴负半轴上,坐标分别(0, -1),(0,2),(0, - 3),···,
∵1000÷3 = 333余1,
∴第1000个点在y轴正半轴上,坐标为(0,334).
(2) (0,2012)是这列点中的第几个点
根据(1)的规律知点 (0,2012)在y轴正半轴上,
设它是第n个点,则 +1 = 2012,
解得:n=6034.
所以(0,2012) 是这列点中的第6034个点.
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
