人教版6下数学 6.2.5《图形与变换》同步练习(含答案)
文档属性
| 名称 | 人教版6下数学 6.2.5《图形与变换》同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 616.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 19:35:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6.2.5《图形与变换》同步练习
班级:_________ 姓名:__________
一、选择题
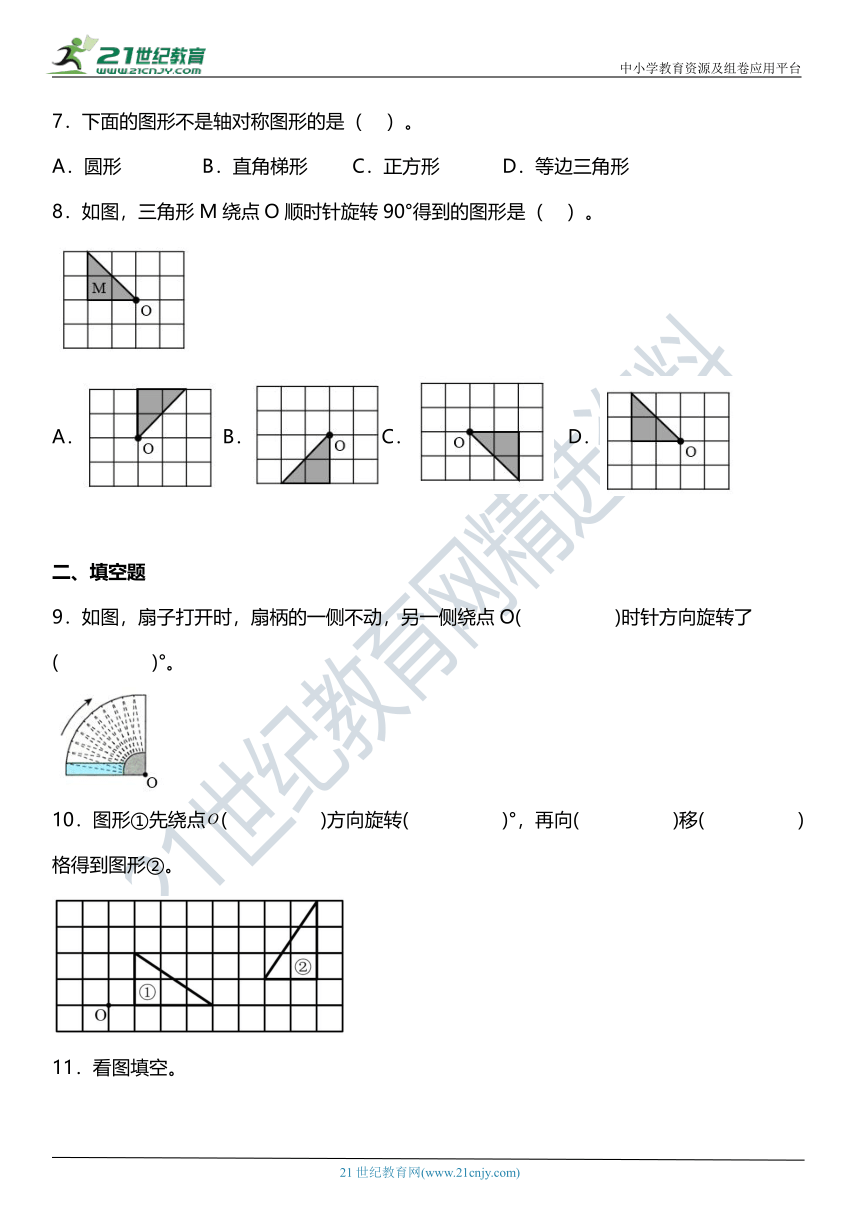
1.夜晚时离路灯越近,物体的影子就( )。
A.越长 B.越短 C.越近 D.越远
2.田田沿着小河游览拍摄风景图(自左向右)。他连续拍了四张照片。这组照片拍摄的先后顺序是( )。
A.4213 B.4231 C.4321 D.1234
3.四个图形中对称轴最多的是( )。
A.长方形 B.正方形 C.等边三角形 D.半圆
4.车轮设计成圆形的原因是( )。
A.周三径一 B.轴对称图形 C.d=2r D.一中同长
5.下列篆字中,属于轴对称图形的有( )。
A.1个 B.2个 C.3个 D.4个
6.在同一个平面内,由大小不同的两个圆组成的图形可能( )。
A.有一条对称轴 B.有两条对称轴
C.有一条或无数条对称轴 D.没有对称轴
7.下面的图形不是轴对称图形的是( )。
A.圆形 B.直角梯形 C.正方形 D.等边三角形
8.如图,三角形M绕点O顺时针旋转90°得到的图形是( )。
A.B.C. D.
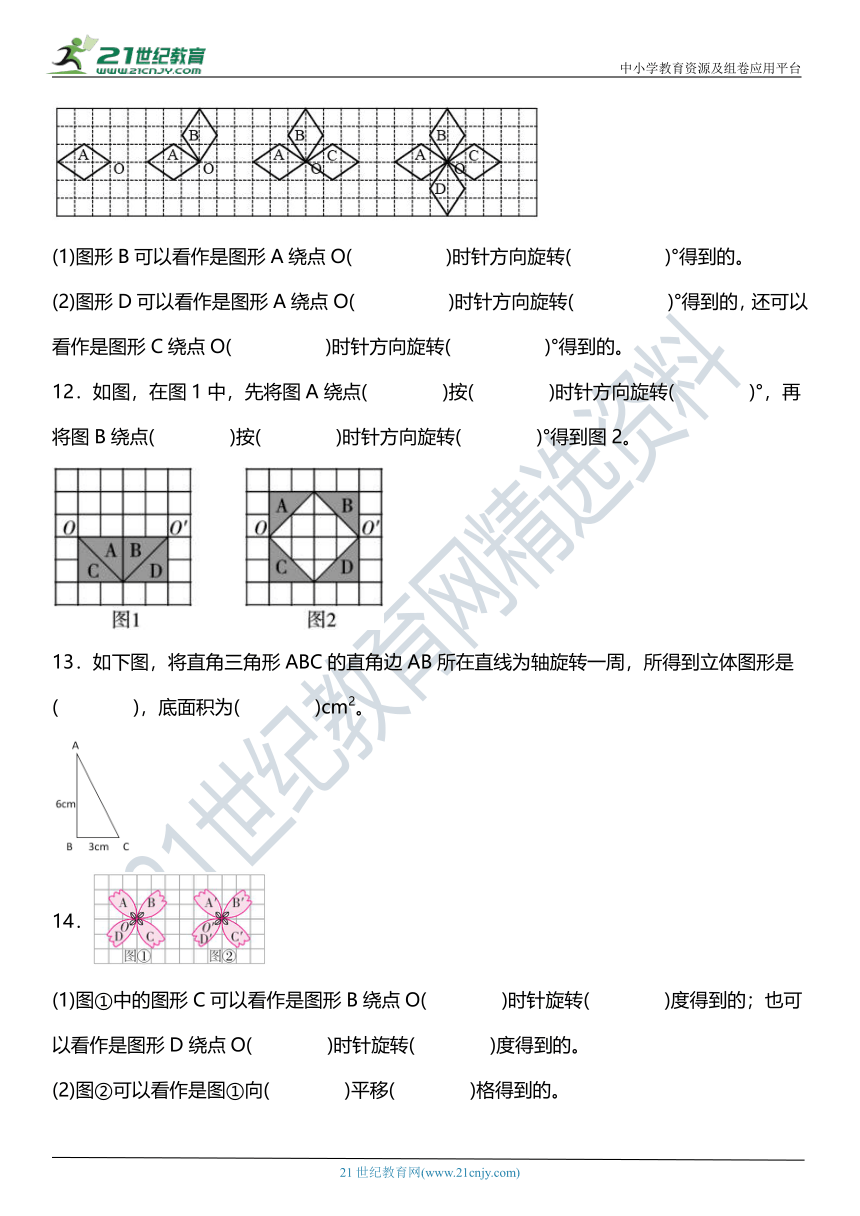
二、填空题
9.如图,扇子打开时,扇柄的一侧不动,另一侧绕点O( )时针方向旋转了( )°。
10.图形①先绕点( )方向旋转( )°,再向( )移( )格得到图形②。
11.看图填空。
(1)图形B可以看作是图形A绕点O( )时针方向旋转( )°得到的。
(2)图形D可以看作是图形A绕点O( )时针方向旋转( )°得到的,还可以看作是图形C绕点O( )时针方向旋转( )°得到的。
12.如图,在图1中,先将图A绕点( )按( )时针方向旋转( )°,再将图B绕点( )按( )时针方向旋转( )°得到图2。
13.如下图,将直角三角形ABC的直角边AB所在直线为轴旋转一周,所得到立体图形是( ),底面积为( )cm2。
14.
(1)图①中的图形C可以看作是图形B绕点O( )时针旋转( )度得到的;也可以看作是图形D绕点O( )时针旋转( )度得到的。
(2)图②可以看作是图①向( )平移( )格得到的。
15.下图指针从“12”绕点0顺时针旋转60°到“( )”;指针从“1”绕点0( )时针旋转60°到“3”;指针从“6”绕点0顺时针旋转180°到“( )”;指针从“10”绕点0( )时针旋转30°到“9”。
16.下面图(2)是将图(1)中半圆BMO以( )点为中心逆时针旋转( )得到的。若A0=5cm,那么图(1)中阴影部分的面积是( )cm2,周长是( )cm。
17.将绕点O按( )时针方向旋转( )度得到图形;将绕其中心点按( )时针方向旋转( )度得到图形。
18.影响图形旋转的因素有( )、( )和( )。
19.观察景物时,景物离得越远,看到景物的范围就越( )。(填“大”或“小”)
20.一个三角形绕着一个顶点旋转270°后,只有三角形的( )改变了,三角形的( )和( )都没有变。
三、判断题
21.图形经过旋转可以得到图形。( )
22.可以由基本图形绕中心点旋转8次产生,每次旋转60度。( )
23.沿着平行四边形的任何一条对角线剪开,可以得到两个完全相同的三角形,所以平行四边形对角线所在的直线是它的对称轴。( )
24.一个长方形绕它的任意一个顶点旋转180°,就可以与它自身重合。( )
25.沿着一个半圆的直径旋转一周,得到的立体图形是球。( )
四、作图题
26.如图,探照灯照不到的位置是哪些地方?请你在图中画一画并用阴影表示出来。
27.(1)将图A向左平移10格。
(2)将图B按点O顺时针方向旋转90°。
(3)以直线L为对称轴,画出已知图形C的轴对称图形。
28.操作。
(1)画出图中三角形按3∶1放大后得到的图形。
(2)将上面的长方形绕点O逆时针方向旋转90°。
五、解答题
29.图形1的四个图形A,B,C,D如何运动得到图形2?
图形1 图形2
30.下图中,图1中的小海豚是一幅由三张卡片组成的图。怎样移动才能将图2恢复到图1?把过程记录下来。
31.如图,苏朋站在阳台前眺望,这时于洋刚走出楼门。
(1)站在阳台上的苏朋能看见于洋吗?
(2)于洋走到什么位置时,苏朋才能看到他?在图上标出来。
32.下面是一个长6厘米,宽3厘米的长方形,根据要求画图或回答问题。
(1)先在长方形里画一个最大的半圆,并用铅笔给它涂上颜色。
(2)所画的半圆与长方形组成的组合图形是轴对称图形吗?如果是,请在图中画出它的对称轴。
(3)求出所画半圆的周长是( )厘米;空白部分的面积是( )平方厘米。
(4)思考:如果是在这个长方形中画最大的圆,那么这个圆的直径长( )厘米。在这个长方形中可以画出( )个这样的圆(不重叠)。
参考答案:
1.B
【分析】连接路灯和物体的顶端并延长交平面于一点,这点到物体的底端的距离就是物体的影长,画出相应图形,比较即可。
【详解】由下图易得,那么离路灯越近,它的影子越短。
故答案为:B
【点睛】本题考查的知识点为:影长是点光源与物高的连线形成的在地面的阴影部分的长度。
2.B
【分析】因为田田沿着小河游览拍摄风景图(自左向右)。所以第一次拍到的是第四张,第二次拍到的是第二张,第三次拍到的是第三张;最后一个拍到的是第一张,据此即可解答。
【详解】田田沿着小河游览拍摄风景图(自左向右)。他连续拍了四张照片。这组照片拍摄的先后顺序是4231。
故答案为:B
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
3.B
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】A.长方形有2条对称轴,
B.正方形有4条对称轴,
C.等边三角形有3条对称轴,
D.半圆有1条对称轴;
4>3>2>1
对称轴最多的是正方形。
故答案为:B
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
4.D
【分析】连接圆心和圆上任意一点的线段叫做半径;半径决定圆的大小,在同一个圆内有无数条半径,同一个圆内所有的半径都相等。把车轴安装在车轮的圆心处,车开起来更平稳,是利用了同一个圆的半径都相等的特性。
【详解】A.“周三径一”的意思是,圆周长大约是直径的3倍;
B.圆沿任意一条直径所在的直线对折,对折后的两部分都能完全重合,所以圆是轴对称图形,任意一条直径所在的直线就是圆的对称轴;
C.d=2r,同一个圆中,直径是半径的2倍;
D.“一中同长”的意思是,每个圆只有一个中心点,从圆心到圆上作线段,长度都相等。
综上所述可知,车轮设计成圆形的原因是同一个圆内半径都相等,也就是一中同长。
故答案为:D
【点睛】本题考查圆的特征在生活中的实际应用。
5.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】由分析可得:篆字中,属于轴对称图形的是、、。
故答案为:C
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
6.C
【分析】依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可解答。
【详解】如图所示,由两个大小不同的圆组成的图形,大约有以下几种情况:
所以在同一个平面内,由两个大小不同的圆组成的图形可能有1条或者无数条对称轴。
故答案为:C
【点睛】解答此题的主要依据是:轴对称图形的概念及特征,借助画图,更容易解答。
7.B
【分析】依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此解答即可。
【详解】A.圆形是轴对称图形,不符合题意;
B.直角梯形不是轴对称图形,符合题意;
C.正方形是轴对称图形,不符合题意;
D.等边三角形是轴对称图形,不符合题意。
故答案为:B
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
8.A
【分析】图形的旋转是图形上的每个点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,且旋转前后图形的大小和形状没有改变,三角形M绕点O顺时针旋转90°,点O的位置不动,三角形M的各部分绕点O按相同的方向旋转相同的度数,据此解答。
【详解】A.三角形M绕点O顺时针旋转90°得到;
B.三角形M绕点O逆时针旋转90°得到;
C.三角形M绕点O顺(逆)时针旋转180°得到;
D.三角形M绕点O顺(逆)时针旋转360°得到。
故答案为:A
【点睛】本题主要考查图形的旋转问题,掌握旋转的特征是解答题目的关键。
9. 顺 90
【分析】根据旋转的特征,扇子打开时,将扇子绕O点顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即顺时针旋转90°,据此解答。
【详解】扇子打开时,扇柄的一侧不动,另一侧绕点O顺时针方向旋转了90°。
【点睛】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
10. 逆时针 90 右 8
【分析】根据旋转的特征,图形①先绕点O逆时针旋转90°,点O的位置不变其余各部分均绕此点按相同的方向旋转相同的度数,即可得到旋转后的图形,再根据图形平移的特征,将图形①旋转后得到的图形的各个顶点向右平移8格,即可得到平移后的图形②,据此解答。
【详解】根据分析可知,图形①先绕点O逆时针方向旋转90°,再向右移8格得到图形②。
【点睛】熟练掌握旋转的特征和平移的特征是解答本题的关键。
11.(1) 顺 90
(2) 逆 90 顺 90
【分析】旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。与时针转动方向相同的是顺时针,反之就是逆时针。
【详解】(1)图形B可以看作是图形A绕点O顺时针方向旋转90°得到的。
(2)图形D可以看作是图形A绕点O逆时针方向旋转90°得到的,还可以看作是图形C绕点O顺时针方向旋转90°得到的。
【点睛】此题考查了旋转的意义及在实际当中的运用。
12. O 逆 90 O′ 顺 90
【分析】根据旋转的特征,在图1中,先将图A绕点O逆时针方向旋转90°,再将图B绕点O′顺时针方向旋转90°即可得到图2。
【详解】
在图1中,先将图A绕点O按逆时针方向旋转90°,再将图B绕点O′按顺时针方向旋转90°得到图2。
【点睛】根据旋转的特征,图1绕点O顺时针旋转90°点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
13. 圆锥 28.26
【分析】如果以三角形直角边AB所在直线为轴旋转一周,其旋转所形成图形是一个圆锥体,圆锥体底面半径为3cm的圆,根据圆的面积公式:S=πr2,代入数据进行解答即可。
【详解】3.14×32
=3.14×9
=28.26(cm2)
所得到立体图形是圆锥,底面积为28.26cm2。
【点睛】此题主要考查了学生对圆锥底面积的计算。
14.(1) 顺 90 逆 90
(2) 右 6
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变;
旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变;据此解答。
【详解】(1)图①中的图形C可以看作是图形B绕点O顺时针旋转90度得到的;也可以看作是图形D绕点O逆时针旋转90度得到的。
(2)图②可以看作是图①向右平移6格得到的。
【点睛】此题考查了平移与旋转的意义及在实际当中的运用。
15. 2 顺 12 逆
【分析】观察钟表可知,钟表上的12大格每两格之间的度数为30°,顺时针是指旋转时与钟表的指针一个方向,逆时针是指与钟表的指针相反的方向;可据此分析指针旋转的具体情况。
【详解】根据分析可知,下图指针从“12”绕点O顺时针旋转60°到“2” ;指针从“1”绕点O顺时旋转60°到“3”;指针从“6”绕点O顺时针旋转180°到“12”;指针从“10”绕点O逆时针旋转30°到“9”。
【点睛】本题主要考查了钟表的认识以及指针的旋转,关键是理解钟表上的12大格每两大格之间的角度为30°。
16. 0 180度 39.25 31.4
【分析】观察图形,根据旋转的特征可知,图形(2)是将图形(1)中半圆BMO以O点为中心,逆时针旋转180度得到,图一的面积是半径为5cm的圆的面积的一半,根据圆的面积公式:面积=π×半径2,代入数据,求出阴影部分面积;阴影部分周长是一个半径为5cm圆的周长的一半,再加上直径是5cm圆的周长,根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】图形(2)是将图形(1)中半圆BMO以O点为中心,逆时针旋转180度得到;
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(cm2)
3.14×5×2÷2+3.14×5
=15.7×2÷2+15.7
=31.4÷2+15.7
=15.7+15.7
=31.4(cm)
下面图(2)是将图(1)中半圆BMO以O点为中心逆时针旋转180度得到的。若A0=5cm,那么图(1)中阴影部分的面积是39.25cm2,周长是31.4cm。
【点睛】利用旋转的特征,圆的周长公式以及面积公式进行解答。
17. 逆 90 顺/逆 90
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度;据此解答。
【详解】根据图形选择的特征及要素可知:绕点O按逆时针方向旋转90度得到图形;绕其中心点按顺(或逆)时针方向旋转90度得到图形。
【点睛】本题主要考查图形的旋转,注意顺逆方向。
18. 旋转中心 旋转方向 旋转角度
【详解】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转;据此解答。
如图所示:
将三角形ABC绕C点顺时针旋转90度,可得旋转后的三角形。这个图形运动中的旋转中心为C点,旋转方向为顺时针,旋转角度为90度,三要素缺一不可。
因此,影响图形旋转的因素有旋转中心、旋转方向与旋转角度。
19.大
【分析】根据生活经验,通过观察物体可知:观察物体时,离得越远看到景物的范围越大,看到的物体越小,越模糊;离得越近看到景物的范围越小,看到的物体越大,越清晰。
【详解】观察物体时,离得越远看到景物的范围越大,看到的物体越小,越模糊;离得越近看到景物的范围越小,看到的物体越大,越清晰。.
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
20. 位置 形状 大小
【分析】旋转:在平面内,将一个图形绕一点按某一个方向转动一定的角度,这样的运动叫做图形的旋转;这个顶点叫做旋转中心,转动的角度叫做旋转角,旋转前后图形的位置和方向改变,形状、大小不变,据此解答。
【详解】根据分析可知,一个三角形绕着一个顶点旋转270°后,只有三角形的位置改变了,三角形的形状和大小都没有变。
【点睛】熟练掌握旋转的特征是解答本题的关键。
21.×
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
【详解】图形经过旋转不能得到图形。
故原题说法错误。
故答案为:×
【点睛】此题考查了平移的意义及在实际当中的运用。
22.×
【分析】在平面内,一个图形绕这个一定点旋转一定的角度得到另一个图形的变化叫做旋转;图形是由8个三角形组成的图案,求出每个图形绕中心点旋转的角度,再进行比较,即可解答。
【详解】360÷8=45(度)
可以由基本图形绕中心点旋转8次产生,每次旋转45度。
原题干说法错误。
故答案为:×
【点睛】解答本题的关键是根据图形特征来判断角度。
23.×
【分析】判断一个图形是否是轴对称图形,需要严格依据定义,必须是沿着某一直线对折,直线两边的部分完全重合。完全重合的两部分必然完全相同,但反之不一定成立。平行四边形沿着对角线折叠之后,两边不能重合,故不是轴对称图形。
【详解】平行四边形沿着对角线折叠之后,两边不能重合,故不是轴对称图形。
原题说法不正确。
故答案为:×
【点睛】本题的关键掌握轴对称图形的判定方法。
24.×
【分析】根据旋转的性质可知,把一个长方形绕一个顶点旋转360°后与原图形重合,依此即可作出判断。
【详解】一个长方形绕它的任意一个顶点旋转360°,就可以与它自身重合,原题说法错误。
故答案为:×
【点睛】本题考查了旋转的知识,需熟练掌握。
25.√
【分析】根据半圆和球的特征可知,以半圆的直径为轴旋转一周,得到的立体图形就是球,据此解答。
【详解】根据分析可知,沿着一个半圆的直径旋转一周,得到的立体图形是球。
原题干说法正确。
故答案为:√
【点睛】本题考查了半圆和球的特征,要熟练掌握并运用。
26.见详解
【分析】光线不会拐弯,墙的后面探照灯照不到。
【详解】
【点睛】知道光是直线传播的,是解答此题的关键。
27.见详解
【分析】(1)根据平移的特征,把图A的各顶点分别向左平移10格,依次连接、涂色即可得到向左平移10格后的图形。
(2)根据旋转的特征,图B绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴L的右边画出图C的关键对称点,依次连接、涂色即可。
【详解】如图:
【点睛】作平移后的图形、作旋转一定度数后的图形、作轴对称图形的关键是确定对应点(对称点)的位置。
28.见详解
【分析】(1)将三角形的各边分别扩大到原来的3倍,再画出扩大后的图形即可;
(2)根据旋转的特征,这个图形绕点O逆时针旋转90°后,点O位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】(1)、(2)画图如下:
【点睛】此题考查了图形的放大与缩小和旋转作图。做图形放大和缩小的题目时,只是图形的边长扩大或缩小,图形的形状不变。旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
29.见详解
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
【详解】图1以正方形的中心为定点,把A向右方平移5格,把B向下方平移5格,把C向上方平移5格,把D向左方平移5格,即可得出图2。
【点睛】此题考查了平移的意义及在实际当中的运用。考查几何图形的变换的题,关键在于认真分析图形,找到它们是怎么变换的。
30.将①向右平移1格;将②先向下平移3格,再绕左上角的点逆时针旋转90度;将③向左平移1格。(答案不唯一)
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】将①向右平移1格;将②先向下平移3格,再绕左上角的点逆时针旋转90度;将③向左平移1格。(答案为不唯一)
【点睛】此题考查了平移与旋转的意义及在实际当中的运用。
31.(1)看不到
(2)见详解
【分析】(1)根据视角与盲区的关系来判断。
(2)根据光的直射作图,求出位置即可。
【详解】(1)观察图形可知,于洋刚走出楼门时,处在苏明的视角盲区,所以苏明看不到于洋;
(2)当于洋走到A处时进入苏明的视野范围,才能看到。如图画红色部分即可看到,
【点睛】本题是结合实际问题来考查学生对视点,视角和盲区的理解能力。
32.(1)见详解
(2)是;见详解
(3)15.42厘米;3.87平方厘米
(4)3;2
【分析】(1)根据题意,在长方形里画一个最大的半圆,因为长方形长的一半正好等于宽3厘米,所以这个最大半圆的半径为3厘米;以长方形长边上的中点为圆心O,以3厘米为半径r,据此画出长方形内最大的半圆,并涂上颜色。
(2)一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
(3)观察图形可知,半圆的周长=圆周长的一半+直径,空白部分的面积=长方形的面积-半圆的面积,根据圆的周长公式C=πd,长方形的面积公式S=ab,圆的面积公式S=πr2,代入数据计算即可。
(4)在这个长方形中画最大的圆,那么圆的直径等于长方形的宽;用长方形的长除以圆的直径,即可得出可以画几个这样的圆。
【详解】(1)6÷2=3(厘米)
在长方形内画一个半径为3厘米的最大半圆,如下图。
(2)组合图形是轴对称图形,对称轴如下图。
(3)半圆的周长:
3.14×6÷2+6
=9.42+6
=15.42(厘米)
空白部分的面积:
6×3-3.14×32÷2
=18-3.14×9÷2
=18-14.13
=3.87(平方厘米)
所画半圆的周长是15.42厘米,空白部分的面积是3.87平方厘米。
(4)最大的圆的直径长3厘米。
6÷3=2(个)
在这个长方形中可以画出2个这样的圆(不重叠)。
【点睛】本题考查在长方形内画最大的半圆、最大的圆以及对称轴,掌握半圆周长的计算方法、圆的面积、长方形的面积公式的运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.2.5《图形与变换》同步练习
班级:_________ 姓名:__________
一、选择题
1.夜晚时离路灯越近,物体的影子就( )。
A.越长 B.越短 C.越近 D.越远
2.田田沿着小河游览拍摄风景图(自左向右)。他连续拍了四张照片。这组照片拍摄的先后顺序是( )。
A.4213 B.4231 C.4321 D.1234
3.四个图形中对称轴最多的是( )。
A.长方形 B.正方形 C.等边三角形 D.半圆
4.车轮设计成圆形的原因是( )。
A.周三径一 B.轴对称图形 C.d=2r D.一中同长
5.下列篆字中,属于轴对称图形的有( )。
A.1个 B.2个 C.3个 D.4个
6.在同一个平面内,由大小不同的两个圆组成的图形可能( )。
A.有一条对称轴 B.有两条对称轴
C.有一条或无数条对称轴 D.没有对称轴
7.下面的图形不是轴对称图形的是( )。
A.圆形 B.直角梯形 C.正方形 D.等边三角形
8.如图,三角形M绕点O顺时针旋转90°得到的图形是( )。
A.B.C. D.
二、填空题
9.如图,扇子打开时,扇柄的一侧不动,另一侧绕点O( )时针方向旋转了( )°。
10.图形①先绕点( )方向旋转( )°,再向( )移( )格得到图形②。
11.看图填空。
(1)图形B可以看作是图形A绕点O( )时针方向旋转( )°得到的。
(2)图形D可以看作是图形A绕点O( )时针方向旋转( )°得到的,还可以看作是图形C绕点O( )时针方向旋转( )°得到的。
12.如图,在图1中,先将图A绕点( )按( )时针方向旋转( )°,再将图B绕点( )按( )时针方向旋转( )°得到图2。
13.如下图,将直角三角形ABC的直角边AB所在直线为轴旋转一周,所得到立体图形是( ),底面积为( )cm2。
14.
(1)图①中的图形C可以看作是图形B绕点O( )时针旋转( )度得到的;也可以看作是图形D绕点O( )时针旋转( )度得到的。
(2)图②可以看作是图①向( )平移( )格得到的。
15.下图指针从“12”绕点0顺时针旋转60°到“( )”;指针从“1”绕点0( )时针旋转60°到“3”;指针从“6”绕点0顺时针旋转180°到“( )”;指针从“10”绕点0( )时针旋转30°到“9”。
16.下面图(2)是将图(1)中半圆BMO以( )点为中心逆时针旋转( )得到的。若A0=5cm,那么图(1)中阴影部分的面积是( )cm2,周长是( )cm。
17.将绕点O按( )时针方向旋转( )度得到图形;将绕其中心点按( )时针方向旋转( )度得到图形。
18.影响图形旋转的因素有( )、( )和( )。
19.观察景物时,景物离得越远,看到景物的范围就越( )。(填“大”或“小”)
20.一个三角形绕着一个顶点旋转270°后,只有三角形的( )改变了,三角形的( )和( )都没有变。
三、判断题
21.图形经过旋转可以得到图形。( )
22.可以由基本图形绕中心点旋转8次产生,每次旋转60度。( )
23.沿着平行四边形的任何一条对角线剪开,可以得到两个完全相同的三角形,所以平行四边形对角线所在的直线是它的对称轴。( )
24.一个长方形绕它的任意一个顶点旋转180°,就可以与它自身重合。( )
25.沿着一个半圆的直径旋转一周,得到的立体图形是球。( )
四、作图题
26.如图,探照灯照不到的位置是哪些地方?请你在图中画一画并用阴影表示出来。
27.(1)将图A向左平移10格。
(2)将图B按点O顺时针方向旋转90°。
(3)以直线L为对称轴,画出已知图形C的轴对称图形。
28.操作。
(1)画出图中三角形按3∶1放大后得到的图形。
(2)将上面的长方形绕点O逆时针方向旋转90°。
五、解答题
29.图形1的四个图形A,B,C,D如何运动得到图形2?
图形1 图形2
30.下图中,图1中的小海豚是一幅由三张卡片组成的图。怎样移动才能将图2恢复到图1?把过程记录下来。
31.如图,苏朋站在阳台前眺望,这时于洋刚走出楼门。
(1)站在阳台上的苏朋能看见于洋吗?
(2)于洋走到什么位置时,苏朋才能看到他?在图上标出来。
32.下面是一个长6厘米,宽3厘米的长方形,根据要求画图或回答问题。
(1)先在长方形里画一个最大的半圆,并用铅笔给它涂上颜色。
(2)所画的半圆与长方形组成的组合图形是轴对称图形吗?如果是,请在图中画出它的对称轴。
(3)求出所画半圆的周长是( )厘米;空白部分的面积是( )平方厘米。
(4)思考:如果是在这个长方形中画最大的圆,那么这个圆的直径长( )厘米。在这个长方形中可以画出( )个这样的圆(不重叠)。
参考答案:
1.B
【分析】连接路灯和物体的顶端并延长交平面于一点,这点到物体的底端的距离就是物体的影长,画出相应图形,比较即可。
【详解】由下图易得,那么离路灯越近,它的影子越短。
故答案为:B
【点睛】本题考查的知识点为:影长是点光源与物高的连线形成的在地面的阴影部分的长度。
2.B
【分析】因为田田沿着小河游览拍摄风景图(自左向右)。所以第一次拍到的是第四张,第二次拍到的是第二张,第三次拍到的是第三张;最后一个拍到的是第一张,据此即可解答。
【详解】田田沿着小河游览拍摄风景图(自左向右)。他连续拍了四张照片。这组照片拍摄的先后顺序是4231。
故答案为:B
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
3.B
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】A.长方形有2条对称轴,
B.正方形有4条对称轴,
C.等边三角形有3条对称轴,
D.半圆有1条对称轴;
4>3>2>1
对称轴最多的是正方形。
故答案为:B
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
4.D
【分析】连接圆心和圆上任意一点的线段叫做半径;半径决定圆的大小,在同一个圆内有无数条半径,同一个圆内所有的半径都相等。把车轴安装在车轮的圆心处,车开起来更平稳,是利用了同一个圆的半径都相等的特性。
【详解】A.“周三径一”的意思是,圆周长大约是直径的3倍;
B.圆沿任意一条直径所在的直线对折,对折后的两部分都能完全重合,所以圆是轴对称图形,任意一条直径所在的直线就是圆的对称轴;
C.d=2r,同一个圆中,直径是半径的2倍;
D.“一中同长”的意思是,每个圆只有一个中心点,从圆心到圆上作线段,长度都相等。
综上所述可知,车轮设计成圆形的原因是同一个圆内半径都相等,也就是一中同长。
故答案为:D
【点睛】本题考查圆的特征在生活中的实际应用。
5.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】由分析可得:篆字中,属于轴对称图形的是、、。
故答案为:C
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
6.C
【分析】依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可解答。
【详解】如图所示,由两个大小不同的圆组成的图形,大约有以下几种情况:
所以在同一个平面内,由两个大小不同的圆组成的图形可能有1条或者无数条对称轴。
故答案为:C
【点睛】解答此题的主要依据是:轴对称图形的概念及特征,借助画图,更容易解答。
7.B
【分析】依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此解答即可。
【详解】A.圆形是轴对称图形,不符合题意;
B.直角梯形不是轴对称图形,符合题意;
C.正方形是轴对称图形,不符合题意;
D.等边三角形是轴对称图形,不符合题意。
故答案为:B
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
8.A
【分析】图形的旋转是图形上的每个点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,且旋转前后图形的大小和形状没有改变,三角形M绕点O顺时针旋转90°,点O的位置不动,三角形M的各部分绕点O按相同的方向旋转相同的度数,据此解答。
【详解】A.三角形M绕点O顺时针旋转90°得到;
B.三角形M绕点O逆时针旋转90°得到;
C.三角形M绕点O顺(逆)时针旋转180°得到;
D.三角形M绕点O顺(逆)时针旋转360°得到。
故答案为:A
【点睛】本题主要考查图形的旋转问题,掌握旋转的特征是解答题目的关键。
9. 顺 90
【分析】根据旋转的特征,扇子打开时,将扇子绕O点顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即顺时针旋转90°,据此解答。
【详解】扇子打开时,扇柄的一侧不动,另一侧绕点O顺时针方向旋转了90°。
【点睛】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
10. 逆时针 90 右 8
【分析】根据旋转的特征,图形①先绕点O逆时针旋转90°,点O的位置不变其余各部分均绕此点按相同的方向旋转相同的度数,即可得到旋转后的图形,再根据图形平移的特征,将图形①旋转后得到的图形的各个顶点向右平移8格,即可得到平移后的图形②,据此解答。
【详解】根据分析可知,图形①先绕点O逆时针方向旋转90°,再向右移8格得到图形②。
【点睛】熟练掌握旋转的特征和平移的特征是解答本题的关键。
11.(1) 顺 90
(2) 逆 90 顺 90
【分析】旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。与时针转动方向相同的是顺时针,反之就是逆时针。
【详解】(1)图形B可以看作是图形A绕点O顺时针方向旋转90°得到的。
(2)图形D可以看作是图形A绕点O逆时针方向旋转90°得到的,还可以看作是图形C绕点O顺时针方向旋转90°得到的。
【点睛】此题考查了旋转的意义及在实际当中的运用。
12. O 逆 90 O′ 顺 90
【分析】根据旋转的特征,在图1中,先将图A绕点O逆时针方向旋转90°,再将图B绕点O′顺时针方向旋转90°即可得到图2。
【详解】
在图1中,先将图A绕点O按逆时针方向旋转90°,再将图B绕点O′按顺时针方向旋转90°得到图2。
【点睛】根据旋转的特征,图1绕点O顺时针旋转90°点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
13. 圆锥 28.26
【分析】如果以三角形直角边AB所在直线为轴旋转一周,其旋转所形成图形是一个圆锥体,圆锥体底面半径为3cm的圆,根据圆的面积公式:S=πr2,代入数据进行解答即可。
【详解】3.14×32
=3.14×9
=28.26(cm2)
所得到立体图形是圆锥,底面积为28.26cm2。
【点睛】此题主要考查了学生对圆锥底面积的计算。
14.(1) 顺 90 逆 90
(2) 右 6
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变;
旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变;据此解答。
【详解】(1)图①中的图形C可以看作是图形B绕点O顺时针旋转90度得到的;也可以看作是图形D绕点O逆时针旋转90度得到的。
(2)图②可以看作是图①向右平移6格得到的。
【点睛】此题考查了平移与旋转的意义及在实际当中的运用。
15. 2 顺 12 逆
【分析】观察钟表可知,钟表上的12大格每两格之间的度数为30°,顺时针是指旋转时与钟表的指针一个方向,逆时针是指与钟表的指针相反的方向;可据此分析指针旋转的具体情况。
【详解】根据分析可知,下图指针从“12”绕点O顺时针旋转60°到“2” ;指针从“1”绕点O顺时旋转60°到“3”;指针从“6”绕点O顺时针旋转180°到“12”;指针从“10”绕点O逆时针旋转30°到“9”。
【点睛】本题主要考查了钟表的认识以及指针的旋转,关键是理解钟表上的12大格每两大格之间的角度为30°。
16. 0 180度 39.25 31.4
【分析】观察图形,根据旋转的特征可知,图形(2)是将图形(1)中半圆BMO以O点为中心,逆时针旋转180度得到,图一的面积是半径为5cm的圆的面积的一半,根据圆的面积公式:面积=π×半径2,代入数据,求出阴影部分面积;阴影部分周长是一个半径为5cm圆的周长的一半,再加上直径是5cm圆的周长,根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】图形(2)是将图形(1)中半圆BMO以O点为中心,逆时针旋转180度得到;
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(cm2)
3.14×5×2÷2+3.14×5
=15.7×2÷2+15.7
=31.4÷2+15.7
=15.7+15.7
=31.4(cm)
下面图(2)是将图(1)中半圆BMO以O点为中心逆时针旋转180度得到的。若A0=5cm,那么图(1)中阴影部分的面积是39.25cm2,周长是31.4cm。
【点睛】利用旋转的特征,圆的周长公式以及面积公式进行解答。
17. 逆 90 顺/逆 90
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度;据此解答。
【详解】根据图形选择的特征及要素可知:绕点O按逆时针方向旋转90度得到图形;绕其中心点按顺(或逆)时针方向旋转90度得到图形。
【点睛】本题主要考查图形的旋转,注意顺逆方向。
18. 旋转中心 旋转方向 旋转角度
【详解】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转;据此解答。
如图所示:
将三角形ABC绕C点顺时针旋转90度,可得旋转后的三角形。这个图形运动中的旋转中心为C点,旋转方向为顺时针,旋转角度为90度,三要素缺一不可。
因此,影响图形旋转的因素有旋转中心、旋转方向与旋转角度。
19.大
【分析】根据生活经验,通过观察物体可知:观察物体时,离得越远看到景物的范围越大,看到的物体越小,越模糊;离得越近看到景物的范围越小,看到的物体越大,越清晰。
【详解】观察物体时,离得越远看到景物的范围越大,看到的物体越小,越模糊;离得越近看到景物的范围越小,看到的物体越大,越清晰。.
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
20. 位置 形状 大小
【分析】旋转:在平面内,将一个图形绕一点按某一个方向转动一定的角度,这样的运动叫做图形的旋转;这个顶点叫做旋转中心,转动的角度叫做旋转角,旋转前后图形的位置和方向改变,形状、大小不变,据此解答。
【详解】根据分析可知,一个三角形绕着一个顶点旋转270°后,只有三角形的位置改变了,三角形的形状和大小都没有变。
【点睛】熟练掌握旋转的特征是解答本题的关键。
21.×
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
【详解】图形经过旋转不能得到图形。
故原题说法错误。
故答案为:×
【点睛】此题考查了平移的意义及在实际当中的运用。
22.×
【分析】在平面内,一个图形绕这个一定点旋转一定的角度得到另一个图形的变化叫做旋转;图形是由8个三角形组成的图案,求出每个图形绕中心点旋转的角度,再进行比较,即可解答。
【详解】360÷8=45(度)
可以由基本图形绕中心点旋转8次产生,每次旋转45度。
原题干说法错误。
故答案为:×
【点睛】解答本题的关键是根据图形特征来判断角度。
23.×
【分析】判断一个图形是否是轴对称图形,需要严格依据定义,必须是沿着某一直线对折,直线两边的部分完全重合。完全重合的两部分必然完全相同,但反之不一定成立。平行四边形沿着对角线折叠之后,两边不能重合,故不是轴对称图形。
【详解】平行四边形沿着对角线折叠之后,两边不能重合,故不是轴对称图形。
原题说法不正确。
故答案为:×
【点睛】本题的关键掌握轴对称图形的判定方法。
24.×
【分析】根据旋转的性质可知,把一个长方形绕一个顶点旋转360°后与原图形重合,依此即可作出判断。
【详解】一个长方形绕它的任意一个顶点旋转360°,就可以与它自身重合,原题说法错误。
故答案为:×
【点睛】本题考查了旋转的知识,需熟练掌握。
25.√
【分析】根据半圆和球的特征可知,以半圆的直径为轴旋转一周,得到的立体图形就是球,据此解答。
【详解】根据分析可知,沿着一个半圆的直径旋转一周,得到的立体图形是球。
原题干说法正确。
故答案为:√
【点睛】本题考查了半圆和球的特征,要熟练掌握并运用。
26.见详解
【分析】光线不会拐弯,墙的后面探照灯照不到。
【详解】
【点睛】知道光是直线传播的,是解答此题的关键。
27.见详解
【分析】(1)根据平移的特征,把图A的各顶点分别向左平移10格,依次连接、涂色即可得到向左平移10格后的图形。
(2)根据旋转的特征,图B绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴L的右边画出图C的关键对称点,依次连接、涂色即可。
【详解】如图:
【点睛】作平移后的图形、作旋转一定度数后的图形、作轴对称图形的关键是确定对应点(对称点)的位置。
28.见详解
【分析】(1)将三角形的各边分别扩大到原来的3倍,再画出扩大后的图形即可;
(2)根据旋转的特征,这个图形绕点O逆时针旋转90°后,点O位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】(1)、(2)画图如下:
【点睛】此题考查了图形的放大与缩小和旋转作图。做图形放大和缩小的题目时,只是图形的边长扩大或缩小,图形的形状不变。旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
29.见详解
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
【详解】图1以正方形的中心为定点,把A向右方平移5格,把B向下方平移5格,把C向上方平移5格,把D向左方平移5格,即可得出图2。
【点睛】此题考查了平移的意义及在实际当中的运用。考查几何图形的变换的题,关键在于认真分析图形,找到它们是怎么变换的。
30.将①向右平移1格;将②先向下平移3格,再绕左上角的点逆时针旋转90度;将③向左平移1格。(答案不唯一)
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】将①向右平移1格;将②先向下平移3格,再绕左上角的点逆时针旋转90度;将③向左平移1格。(答案为不唯一)
【点睛】此题考查了平移与旋转的意义及在实际当中的运用。
31.(1)看不到
(2)见详解
【分析】(1)根据视角与盲区的关系来判断。
(2)根据光的直射作图,求出位置即可。
【详解】(1)观察图形可知,于洋刚走出楼门时,处在苏明的视角盲区,所以苏明看不到于洋;
(2)当于洋走到A处时进入苏明的视野范围,才能看到。如图画红色部分即可看到,
【点睛】本题是结合实际问题来考查学生对视点,视角和盲区的理解能力。
32.(1)见详解
(2)是;见详解
(3)15.42厘米;3.87平方厘米
(4)3;2
【分析】(1)根据题意,在长方形里画一个最大的半圆,因为长方形长的一半正好等于宽3厘米,所以这个最大半圆的半径为3厘米;以长方形长边上的中点为圆心O,以3厘米为半径r,据此画出长方形内最大的半圆,并涂上颜色。
(2)一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
(3)观察图形可知,半圆的周长=圆周长的一半+直径,空白部分的面积=长方形的面积-半圆的面积,根据圆的周长公式C=πd,长方形的面积公式S=ab,圆的面积公式S=πr2,代入数据计算即可。
(4)在这个长方形中画最大的圆,那么圆的直径等于长方形的宽;用长方形的长除以圆的直径,即可得出可以画几个这样的圆。
【详解】(1)6÷2=3(厘米)
在长方形内画一个半径为3厘米的最大半圆,如下图。
(2)组合图形是轴对称图形,对称轴如下图。
(3)半圆的周长:
3.14×6÷2+6
=9.42+6
=15.42(厘米)
空白部分的面积:
6×3-3.14×32÷2
=18-3.14×9÷2
=18-14.13
=3.87(平方厘米)
所画半圆的周长是15.42厘米,空白部分的面积是3.87平方厘米。
(4)最大的圆的直径长3厘米。
6÷3=2(个)
在这个长方形中可以画出2个这样的圆(不重叠)。
【点睛】本题考查在长方形内画最大的半圆、最大的圆以及对称轴,掌握半圆周长的计算方法、圆的面积、长方形的面积公式的运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
