上海市浦东新区川沙镇川沙学校2022-2023学年高二下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 上海市浦东新区川沙镇川沙学校2022-2023学年高二下学期期中考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 483.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 19:22:13 | ||
图片预览




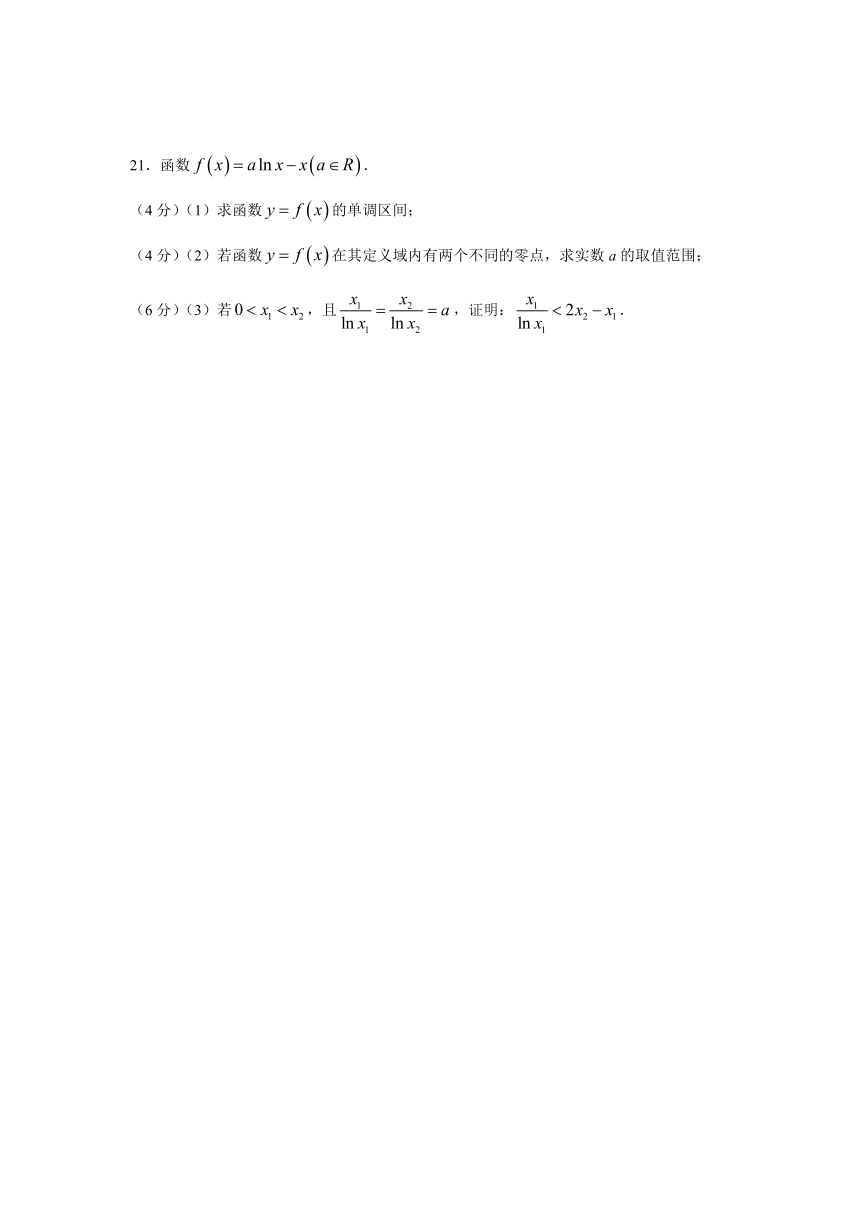
文档简介
川沙学校2022学年第二学期高二年级数学期中
2023.3
一、填空题()
1.函数从到的平均变化率是______.
2.已知函数的图像在点处的切线方程是,则______.
3.若,则______.
4.已知函数的导函数为,且满足关系式,则______.
5.已知国外某地新冠病毒感染率为0.5%,市民感染新冠病毒且标本检出阳性的概率99%,若该地全员参加核酸检测,则该地某市民感染新冠病毒且标本检出阳性的概率是______.(用数值表示)
6.已知函数,则该函数图像在点处的切线的倾斜角的大小是______.
7.某个品种的小麦麦穗长度(单位:cm)的样本数据如下:10.2、9.7、10.8、9.1、8.9、8.6、9.8、9.6、9.9、11.2、10.6、11.7,则这组数据的第80百分位数是______.
8.函数在区间内最小值是______.
9.已知函数(m为实数),若在上单调递减,则实数m的取值范围是______.
10.若函数既有极大值又有极小值,则实数a的取值范围是______.
11.已知,若对任意,都有成立,则实数a的取值范围是______.
12.已知定义在上的函数,其导函数为,若,,则不等式的解集是______.
二、选择题()
13.研究下列问题:①某城市元旦前后的气温;②某种新型电器元件使用寿命的测定;③电视台想知道某一个节目的收视率;④银行在收进储户现金时想知道有没有假钞;一般通过实验获取数据的是( )
A.①② B.③④ C.② D.④
14.已知函数的导函数的图象如图所示,则下列结论中正确的是( )
A.曲线在点处的切线斜率小于零
B.函数在区间上是严格增函数
C.函数在处取得极大值
D.函数在区间内至多有两个零点
15.已知P是曲线上的动点,点Q在直线上运动,则当取最小值时,点P的横坐标是( )
A. B. C. D.
16.甲、乙两位同学进行羽毛球比赛,约定赛制如下:累计赢3局者胜,分出胜负即停止比赛.已知前3局每局甲赢的概率为,之后每局甲赢的概率为,每局比赛没有平局,则打完第5局比赛结束的概率是( )
A. B. C. D.
三、解答题()
17.如图,圆锥的底面半径,高,点C是底面直径AB所对弧的中点,点D是母线PA的中点.求:
(4分)(1)该圆锥的表面积;
(4分)(2)直线CD与平面PAB所成角的大小.
18.某中学将举行趣味运动会.某班共有8名同学报名参加“四人五足”游戏,其中男同学4名,女同学4名.按照游戏规则,每班只能选4名同学参加这个游戏,因此要从这8名报名的同学中随机选出4名.
(4分)(1)求选出的4名同学中有男生的概率;
(4分)(2)记选出的4名同学中女同学的人数为X,求随机变量X的分布列及数学期望.
19.某网球中心在10000平方米土地上,欲建数块连成片的网球场.每块球场的建设面积为1000平方米.当该中心建设块球场时,每平方米的平均建设费用(单位:元)可近似地用函数关系式来刻画,此外该中心还需为该工程一次性向政府缴纳环保费用1280000元.
(5 分)(1)请写出当网球中心建设块球场时,该工程每平方米的综合费用的表达式,并指出其定义域(综合费用是建设费用与环保费用之和);
(5分)(2)为了使该工程每平方米的综合费用最省,该网球中心应建多少个球场?
20.已知A、B分别为椭圆的上、下顶点,F是椭圆的右焦点,是椭圆上异于A、B的点.
(3分)(1)若,求椭圆的标准方程;
(4分)(2)设直线与y轴交于点P,与直线MA交于点Q,与直线MB交于点R,求证:的值仅与a有关;
(5分)(3)如图,在四边形MADB中,,,若四边形MADB面积S的最大值为,求a的值.
21.函数.
(4分)(1)求函数的单调区间;
(4分)(2)若函数在其定义域内有两个不同的零点,求实数a的取值范围;
(6分)(3)若,且,证明:.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6. ; 7.;
8.; 9.; 10.; 11. 12.
12.已知定义在上的函数,其导函数为,若,,则不等式的解集是______.
【答案】
【解析】
令,则,在上单调递减,
,,的解集为.
二、选择题
13.C 14.D 15.C 16.B
15.已知P是曲线上的动点,点Q在直线上运动,则当取最小值时,点P的横坐标是( )
A. B. C. D.
【答案】C
【解析】是曲线上的动点,点在直线上运动,直线的斜率为,则当取最小值时,曲线的切线斜率
,即结合所给的选项,可得即点的横坐标为,故选:.
16.甲、乙两位同学进行羽毛球比赛,约定赛制如下:累计赢3局者胜,分出胜负即停止比赛.已知前3局每局甲赢的概率为,之后每局甲赢的概率为,每局比赛没有平局,则打完第5局比赛结束的概率是( )
A. B. C. D.
【答案】B
【解析】打完第5局比赛结束,包含以下两种情况,
(1)第5局甲赢,前三局甲赢两局,第四局甲输或前三局甲赢一局,第四局甲赢,
概率为
(2)第5局乙赢,前三局乙赢两局,第四局乙输或前三局乙赢一局,第四局乙赢,
概率为
打完第5局比赛结束的概率为故选:.
三.解答题
17.(1)表面积 (2)
18.(1) (2)
19.(1) (2)
20.已知A、B分别为椭圆的上、下顶点,F是椭圆的右焦点,是椭圆上异于A、B的点.
(3分)(1)若,求椭圆的标准方程;
(4分)(2)设直线与y轴交于点P,与直线MA交于点Q,与直线MB交于点R,求证:的值仅与a有关;
(5分)(3)如图,在四边形MADB中,,,若四边形MADB面积S的最大值为,求a的值.
【答案】(1) (2)见解析 (3)
【解析】(1)因为
所以,所以椭圆的标准方程为.
(2)证明:设,2),因为,
所以直线的方程分别为
所以的值仅与有关.
(3)设,
因为,所以,,
两式相减得,代回原式得,因为,所以,
所以四边形的面积为
因为的最大值为,所以,解得因为,所以.
21.函数.
(4分)(1)求函数的单调区间;
(4分)(2)若函数在其定义域内有两个不同的零点,求实数a的取值范围;
(6分)(3)若,且,证明:.
【答案】(1)当时,函数的单调递减区间为;
当时,函数的单调递增区间为,单调递减区间为;
(2)实数的取值范围为
(3)见解析
【解析】(1)函数定义域为,
,,
①当时,在上恒成立,即函数的单调递减区间为;
②当时,,解得,
当时,函数的单调递增区间为,
当时,函数的单调递减区间为,
综上可知:当时,函数的单调递减区间为;
当时,函数的单调递增区间为,单调递减区间为;
(2)由(1)知,当时,函数在上单调递减,
函数至多有一个零点,不符合题意,
当时,函数在上单调递增,
在上单调递减,,
又函数有两个零点,,,
又,使得,
又,
设
上单调递减,,,使得,
综上可知,为所求.实数的取值范围为.
(3)证明:依题意,是函数的两个零点,
设,因为,
不等式
在上是增函数,且,
即,从而.
2023.3
一、填空题()
1.函数从到的平均变化率是______.
2.已知函数的图像在点处的切线方程是,则______.
3.若,则______.
4.已知函数的导函数为,且满足关系式,则______.
5.已知国外某地新冠病毒感染率为0.5%,市民感染新冠病毒且标本检出阳性的概率99%,若该地全员参加核酸检测,则该地某市民感染新冠病毒且标本检出阳性的概率是______.(用数值表示)
6.已知函数,则该函数图像在点处的切线的倾斜角的大小是______.
7.某个品种的小麦麦穗长度(单位:cm)的样本数据如下:10.2、9.7、10.8、9.1、8.9、8.6、9.8、9.6、9.9、11.2、10.6、11.7,则这组数据的第80百分位数是______.
8.函数在区间内最小值是______.
9.已知函数(m为实数),若在上单调递减,则实数m的取值范围是______.
10.若函数既有极大值又有极小值,则实数a的取值范围是______.
11.已知,若对任意,都有成立,则实数a的取值范围是______.
12.已知定义在上的函数,其导函数为,若,,则不等式的解集是______.
二、选择题()
13.研究下列问题:①某城市元旦前后的气温;②某种新型电器元件使用寿命的测定;③电视台想知道某一个节目的收视率;④银行在收进储户现金时想知道有没有假钞;一般通过实验获取数据的是( )
A.①② B.③④ C.② D.④
14.已知函数的导函数的图象如图所示,则下列结论中正确的是( )
A.曲线在点处的切线斜率小于零
B.函数在区间上是严格增函数
C.函数在处取得极大值
D.函数在区间内至多有两个零点
15.已知P是曲线上的动点,点Q在直线上运动,则当取最小值时,点P的横坐标是( )
A. B. C. D.
16.甲、乙两位同学进行羽毛球比赛,约定赛制如下:累计赢3局者胜,分出胜负即停止比赛.已知前3局每局甲赢的概率为,之后每局甲赢的概率为,每局比赛没有平局,则打完第5局比赛结束的概率是( )
A. B. C. D.
三、解答题()
17.如图,圆锥的底面半径,高,点C是底面直径AB所对弧的中点,点D是母线PA的中点.求:
(4分)(1)该圆锥的表面积;
(4分)(2)直线CD与平面PAB所成角的大小.
18.某中学将举行趣味运动会.某班共有8名同学报名参加“四人五足”游戏,其中男同学4名,女同学4名.按照游戏规则,每班只能选4名同学参加这个游戏,因此要从这8名报名的同学中随机选出4名.
(4分)(1)求选出的4名同学中有男生的概率;
(4分)(2)记选出的4名同学中女同学的人数为X,求随机变量X的分布列及数学期望.
19.某网球中心在10000平方米土地上,欲建数块连成片的网球场.每块球场的建设面积为1000平方米.当该中心建设块球场时,每平方米的平均建设费用(单位:元)可近似地用函数关系式来刻画,此外该中心还需为该工程一次性向政府缴纳环保费用1280000元.
(5 分)(1)请写出当网球中心建设块球场时,该工程每平方米的综合费用的表达式,并指出其定义域(综合费用是建设费用与环保费用之和);
(5分)(2)为了使该工程每平方米的综合费用最省,该网球中心应建多少个球场?
20.已知A、B分别为椭圆的上、下顶点,F是椭圆的右焦点,是椭圆上异于A、B的点.
(3分)(1)若,求椭圆的标准方程;
(4分)(2)设直线与y轴交于点P,与直线MA交于点Q,与直线MB交于点R,求证:的值仅与a有关;
(5分)(3)如图,在四边形MADB中,,,若四边形MADB面积S的最大值为,求a的值.
21.函数.
(4分)(1)求函数的单调区间;
(4分)(2)若函数在其定义域内有两个不同的零点,求实数a的取值范围;
(6分)(3)若,且,证明:.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6. ; 7.;
8.; 9.; 10.; 11. 12.
12.已知定义在上的函数,其导函数为,若,,则不等式的解集是______.
【答案】
【解析】
令,则,在上单调递减,
,,的解集为.
二、选择题
13.C 14.D 15.C 16.B
15.已知P是曲线上的动点,点Q在直线上运动,则当取最小值时,点P的横坐标是( )
A. B. C. D.
【答案】C
【解析】是曲线上的动点,点在直线上运动,直线的斜率为,则当取最小值时,曲线的切线斜率
,即结合所给的选项,可得即点的横坐标为,故选:.
16.甲、乙两位同学进行羽毛球比赛,约定赛制如下:累计赢3局者胜,分出胜负即停止比赛.已知前3局每局甲赢的概率为,之后每局甲赢的概率为,每局比赛没有平局,则打完第5局比赛结束的概率是( )
A. B. C. D.
【答案】B
【解析】打完第5局比赛结束,包含以下两种情况,
(1)第5局甲赢,前三局甲赢两局,第四局甲输或前三局甲赢一局,第四局甲赢,
概率为
(2)第5局乙赢,前三局乙赢两局,第四局乙输或前三局乙赢一局,第四局乙赢,
概率为
打完第5局比赛结束的概率为故选:.
三.解答题
17.(1)表面积 (2)
18.(1) (2)
19.(1) (2)
20.已知A、B分别为椭圆的上、下顶点,F是椭圆的右焦点,是椭圆上异于A、B的点.
(3分)(1)若,求椭圆的标准方程;
(4分)(2)设直线与y轴交于点P,与直线MA交于点Q,与直线MB交于点R,求证:的值仅与a有关;
(5分)(3)如图,在四边形MADB中,,,若四边形MADB面积S的最大值为,求a的值.
【答案】(1) (2)见解析 (3)
【解析】(1)因为
所以,所以椭圆的标准方程为.
(2)证明:设,2),因为,
所以直线的方程分别为
所以的值仅与有关.
(3)设,
因为,所以,,
两式相减得,代回原式得,因为,所以,
所以四边形的面积为
因为的最大值为,所以,解得因为,所以.
21.函数.
(4分)(1)求函数的单调区间;
(4分)(2)若函数在其定义域内有两个不同的零点,求实数a的取值范围;
(6分)(3)若,且,证明:.
【答案】(1)当时,函数的单调递减区间为;
当时,函数的单调递增区间为,单调递减区间为;
(2)实数的取值范围为
(3)见解析
【解析】(1)函数定义域为,
,,
①当时,在上恒成立,即函数的单调递减区间为;
②当时,,解得,
当时,函数的单调递增区间为,
当时,函数的单调递减区间为,
综上可知:当时,函数的单调递减区间为;
当时,函数的单调递增区间为,单调递减区间为;
(2)由(1)知,当时,函数在上单调递减,
函数至多有一个零点,不符合题意,
当时,函数在上单调递增,
在上单调递减,,
又函数有两个零点,,,
又,使得,
又,
设
上单调递减,,,使得,
综上可知,为所求.实数的取值范围为.
(3)证明:依题意,是函数的两个零点,
设,因为,
不等式
在上是增函数,且,
即,从而.
同课章节目录
