5.4.1正弦函数、余弦函数图象-高中数学人教A版必修一同步课件(共23张PPT)
文档属性
| 名称 | 5.4.1正弦函数、余弦函数图象-高中数学人教A版必修一同步课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 21:24:01 | ||
图片预览




文档简介
(共23张PPT)
数 学
数 学
题型一 正弦函数、余弦函数图象的初步认识
知识梳理
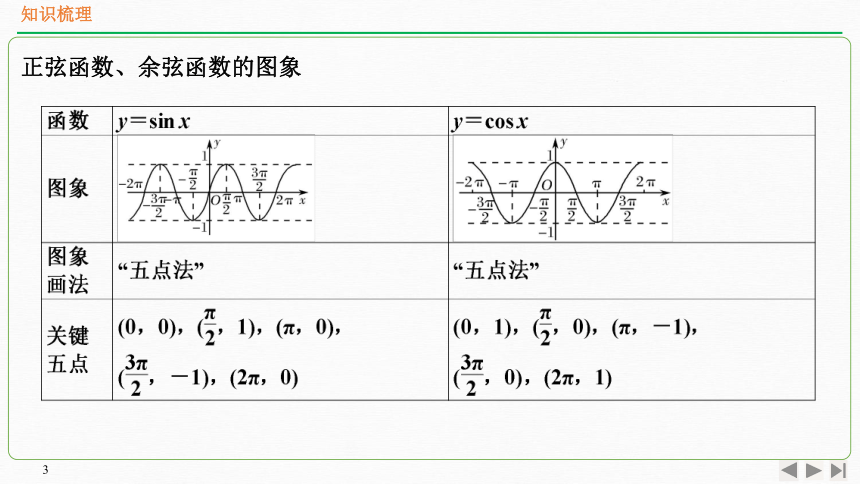
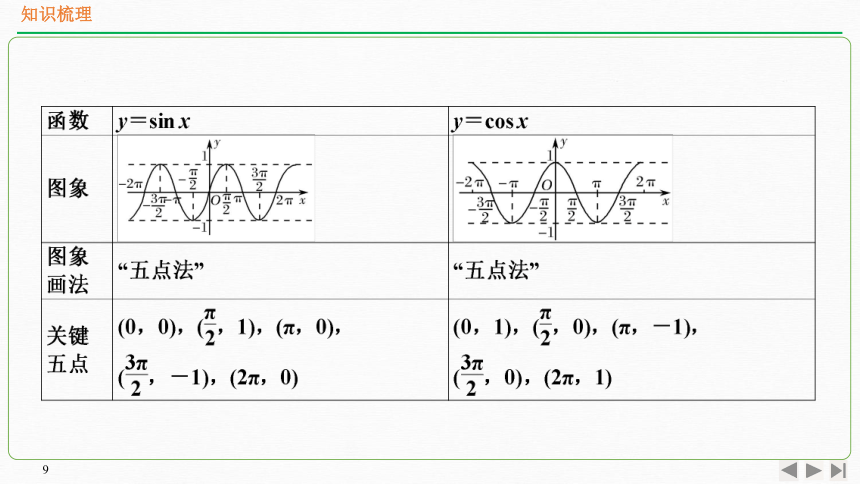
正弦函数、余弦函数的图象
课堂精讲
【例1】 (1)下列叙述正确的个数为( )
①y=sin x,x∈[0,2π]的图象关于点P(π,0)成中心对称;
②y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称;
③正、余弦函数的图象不超过直线y=1和y=-1所夹的范围.
A.0 B.1个 C.2个 D.3个
y=x2-5x-6
解析 (1)分别画出函数y=sin x,x∈[0,2π]
和y=cos x,x∈[0,2π]的图象,
由图象(略)观察可知①②③均正确.
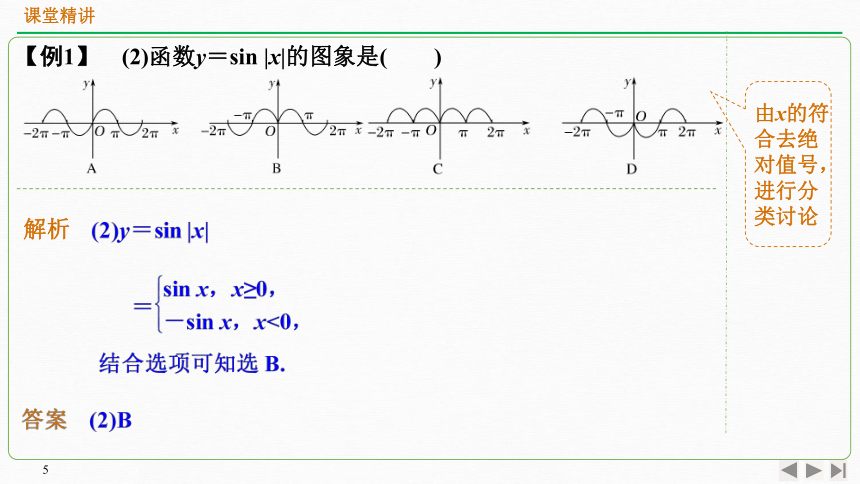
答案 (2)B
课堂精讲
【例1】 (2)函数y=sin |x|的图象是( )
解析
y=x2-5x-6
由x的符合去绝对值号,进行分类讨论
课堂精讲
解决正、余弦函数图象的注意点
对于正、余弦函数的图象问题,要画出正确的正弦曲线、余弦曲线,掌握两者的形状相同,只是在坐标系中的位置不同,可以通过相互平移得到.
课堂精炼
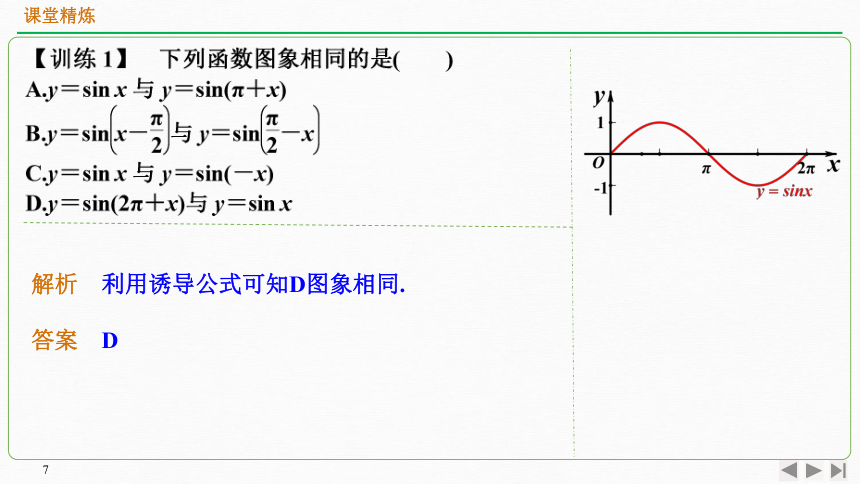
解析 利用诱导公式可知D图象相同.
答案 D
数 学
题型二 “五点法”作图的应用
知识梳理
;
课堂精讲
解 (1)取值列表:
“五点法”作图象步骤如下:
(1)列表
(2)描点
(3)连线
(2)描点连线,如图所示.
课堂精讲
课堂精炼
“五点法”作图象步骤如下:
(1)列表
(2)描点
(3)连线
数 学
题型三 正弦、余弦函数图象的应用
知识梳理
1.(1)正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线.
(2)余弦函数y=cos x,x∈R的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
2.正弦函数、余弦函数的值域
(1)y=sin x,x∈R的值域为[-1,1];
(2)y=cos x,x∈R的值域为[-1,1].
课堂精讲
课堂精讲
用三角函数图象解三角不等式的方法
(1)作出相应正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出不等式的解集.
课堂精讲
课堂精讲
课堂精讲
求三角函数定义域时,常常归结为解三角不等式(组),这时可利用基本三角函数的图象直观地求得解集.
课堂精炼
求三角函数定义域时,常常归结为解三角不等式(组),这时可利用基本三角函数的图象直观地求得解集.
课堂精炼
求三角函数定义域时,常常归结为解三角不等式(组),这时可利用基本三角函数的图象直观地求得解集.
课堂小结
1.通过本节课的作图和正、余弦函数图象的应用,重点提升学生的数学抽象、逻辑推理和直观想象素养.
2.对“五点法”画正弦函数图象的理解
(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.
(2)正弦函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.
3.作函数y=asin x+b的图象的步骤
数 学
数 学
题型一 正弦函数、余弦函数图象的初步认识
知识梳理
正弦函数、余弦函数的图象
课堂精讲
【例1】 (1)下列叙述正确的个数为( )
①y=sin x,x∈[0,2π]的图象关于点P(π,0)成中心对称;
②y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称;
③正、余弦函数的图象不超过直线y=1和y=-1所夹的范围.
A.0 B.1个 C.2个 D.3个
y=x2-5x-6
解析 (1)分别画出函数y=sin x,x∈[0,2π]
和y=cos x,x∈[0,2π]的图象,
由图象(略)观察可知①②③均正确.
答案 (2)B
课堂精讲
【例1】 (2)函数y=sin |x|的图象是( )
解析
y=x2-5x-6
由x的符合去绝对值号,进行分类讨论
课堂精讲
解决正、余弦函数图象的注意点
对于正、余弦函数的图象问题,要画出正确的正弦曲线、余弦曲线,掌握两者的形状相同,只是在坐标系中的位置不同,可以通过相互平移得到.
课堂精炼
解析 利用诱导公式可知D图象相同.
答案 D
数 学
题型二 “五点法”作图的应用
知识梳理
;
课堂精讲
解 (1)取值列表:
“五点法”作图象步骤如下:
(1)列表
(2)描点
(3)连线
(2)描点连线,如图所示.
课堂精讲
课堂精炼
“五点法”作图象步骤如下:
(1)列表
(2)描点
(3)连线
数 学
题型三 正弦、余弦函数图象的应用
知识梳理
1.(1)正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线.
(2)余弦函数y=cos x,x∈R的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
2.正弦函数、余弦函数的值域
(1)y=sin x,x∈R的值域为[-1,1];
(2)y=cos x,x∈R的值域为[-1,1].
课堂精讲
课堂精讲
用三角函数图象解三角不等式的方法
(1)作出相应正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出不等式的解集.
课堂精讲
课堂精讲
课堂精讲
求三角函数定义域时,常常归结为解三角不等式(组),这时可利用基本三角函数的图象直观地求得解集.
课堂精炼
求三角函数定义域时,常常归结为解三角不等式(组),这时可利用基本三角函数的图象直观地求得解集.
课堂精炼
求三角函数定义域时,常常归结为解三角不等式(组),这时可利用基本三角函数的图象直观地求得解集.
课堂小结
1.通过本节课的作图和正、余弦函数图象的应用,重点提升学生的数学抽象、逻辑推理和直观想象素养.
2.对“五点法”画正弦函数图象的理解
(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.
(2)正弦函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.
3.作函数y=asin x+b的图象的步骤
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
