5.4.2正弦函数与余弦函数的性质课件 第二课时-高中数学人教A版必修一同步课件(共23张PPT)
文档属性
| 名称 | 5.4.2正弦函数与余弦函数的性质课件 第二课时-高中数学人教A版必修一同步课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 21:24:33 | ||
图片预览




文档简介
(共23张PPT)
数 学
数 学
题型一 正弦、余弦函数的单调性
知识梳理
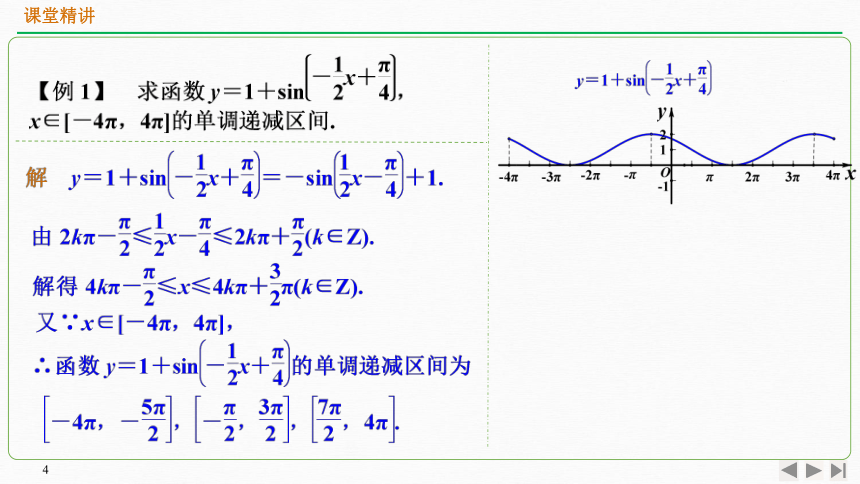
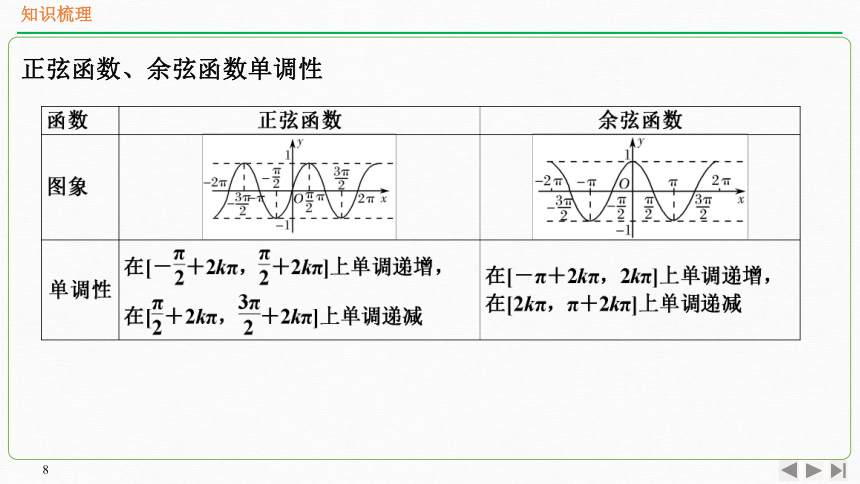
正弦函数、余弦函数单调性
课堂精讲
课堂精讲
用整体替换法求函数y=Asin(ωx+φ)或y=Acos(ωx+φ)的单调区间时,如果式子中x的系数为负数,先利用诱导公式将x的系数变为正数再求其单调区间.求单调区间时,需将最终结果写成区间形式.
课堂精讲
数 学
题型二 利用正弦、余弦函数的单调性比较大小
知识梳理
正弦函数、余弦函数单调性
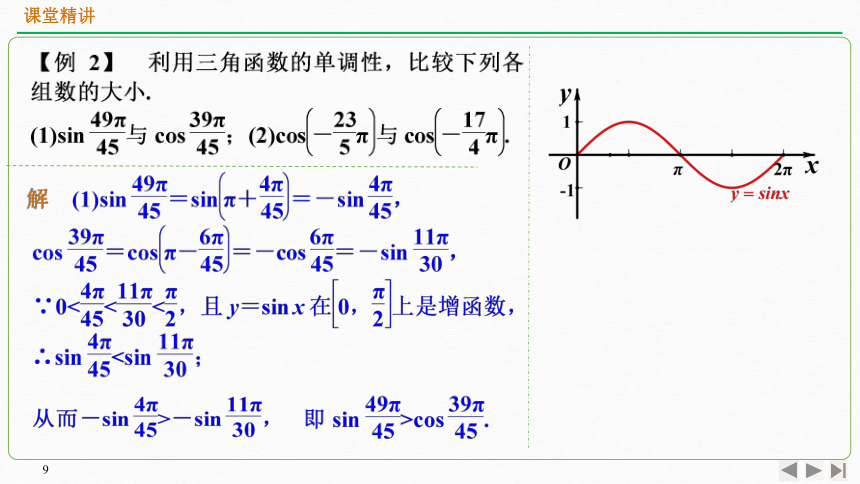
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂精讲
课堂精讲
数 学
题型三 正弦、余弦函数的最值(值域)问题
知识梳理
课堂精讲
课堂精讲
解 y=cos2x-4cos x+5,
令t=cos x,则-1≤t≤1.
y=t2-4t+5=(t-2)2+1,
当t=-1,函数取得最大值10;
t=1时,函数取得最小值2,
所以函数的值域为[2,10].
y=t2-4+5 , -1≤t≤1
课堂精讲
求三角函数值域或最值的常用方法
(1)形如y=sin(ωx+φ)的三角函数,令t=ωx+φ,根据题中x的取值范围,求出t的取值范围,再利用三角函数的单调性、有界性求出y=sin t的最值(值域).
(2)形如y=asin2x+bsin x+c(a≠0)的三角函数,可先设t=sin x,将函数y=asin2x+bsin x+c(a≠0)化为关于t的二次函数y=at2+bt+c(a≠0),根据二次函数的单调性求值域(最值).
(3)对于形如y=asin x(或y=acos x)的函数的最值还要注意对a的讨论.
课堂精炼
课堂小结
课堂小结
3.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断.
4.求三角函数值域或最值的常用方法:
将y表示成以sin x(或cos x)为元的一次或二次等复合函数,再利用换元或配方或利用函数的单调性等来确定y的范围.
通过上述问题,不断提高学生的数学运算、逻辑推理的素养.
数 学
数 学
题型一 正弦、余弦函数的单调性
知识梳理
正弦函数、余弦函数单调性
课堂精讲
课堂精讲
用整体替换法求函数y=Asin(ωx+φ)或y=Acos(ωx+φ)的单调区间时,如果式子中x的系数为负数,先利用诱导公式将x的系数变为正数再求其单调区间.求单调区间时,需将最终结果写成区间形式.
课堂精讲
数 学
题型二 利用正弦、余弦函数的单调性比较大小
知识梳理
正弦函数、余弦函数单调性
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂精讲
课堂精讲
数 学
题型三 正弦、余弦函数的最值(值域)问题
知识梳理
课堂精讲
课堂精讲
解 y=cos2x-4cos x+5,
令t=cos x,则-1≤t≤1.
y=t2-4t+5=(t-2)2+1,
当t=-1,函数取得最大值10;
t=1时,函数取得最小值2,
所以函数的值域为[2,10].
y=t2-4+5 , -1≤t≤1
课堂精讲
求三角函数值域或最值的常用方法
(1)形如y=sin(ωx+φ)的三角函数,令t=ωx+φ,根据题中x的取值范围,求出t的取值范围,再利用三角函数的单调性、有界性求出y=sin t的最值(值域).
(2)形如y=asin2x+bsin x+c(a≠0)的三角函数,可先设t=sin x,将函数y=asin2x+bsin x+c(a≠0)化为关于t的二次函数y=at2+bt+c(a≠0),根据二次函数的单调性求值域(最值).
(3)对于形如y=asin x(或y=acos x)的函数的最值还要注意对a的讨论.
课堂精炼
课堂小结
课堂小结
3.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断.
4.求三角函数值域或最值的常用方法:
将y表示成以sin x(或cos x)为元的一次或二次等复合函数,再利用换元或配方或利用函数的单调性等来确定y的范围.
通过上述问题,不断提高学生的数学运算、逻辑推理的素养.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
