5.6 函数y=Asin(ωx+φ) 第一课时-高中数学人教A版必修一同步课件(共27张PPT)
文档属性
| 名称 | 5.6 函数y=Asin(ωx+φ) 第一课时-高中数学人教A版必修一同步课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 21:43:11 | ||
图片预览






文档简介
(共27张PPT)
数 学
数 学
题型一 “五点法”作函数y=Asin(ωx+φ)的图象
知识梳理
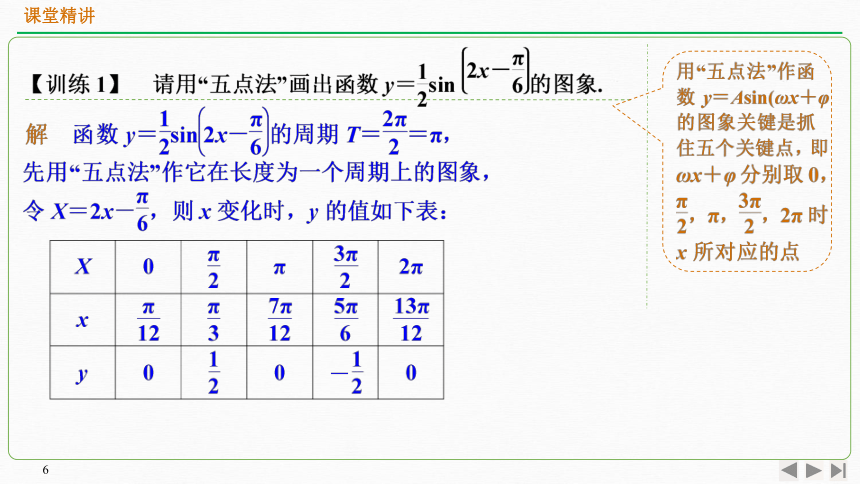
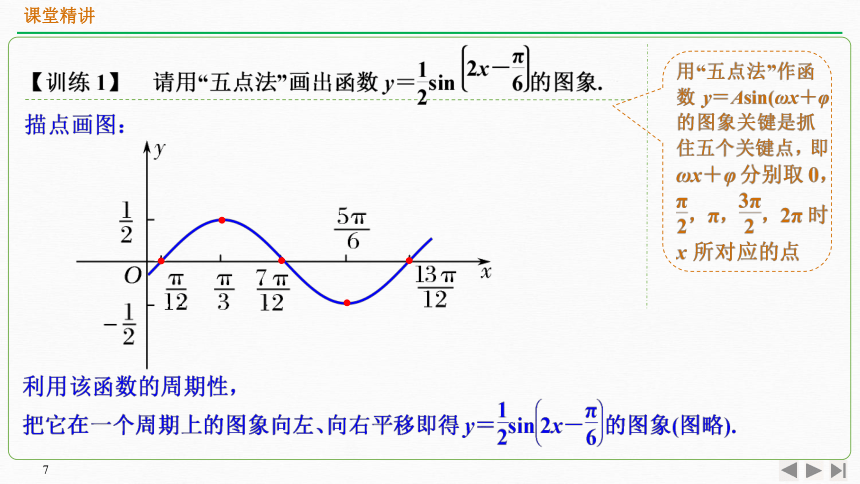
用“五点法”作函数y=Asin(ωx+φ)的图象关键是抓住五个关键点,即三个“平衡点”(即ωx+φ分别取0,π,2π时x所对应的点) 、一个“波峰点”、一个“波谷点”.
课堂精讲
课堂精讲
课堂精讲
课堂精讲
数 学
题型二 三角函数图象的平移变换
知识梳理
1.φ对函数y=sin(x+φ),x∈R的图象的影响
;
2. φ 对函数y=sin(ωx+φ) ,(ω>0)图象的影响
y=sinωx
的图象
φ>0时向左
y=sin(ωx+φ) 图象
φ<0时向右
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
三角函数图象平移变换问题的分类及策略
(1)确定函数y=sin x的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
(2)已知两个函数解析式判断其图象间的平移关系时,首先要将解析式化为同名三角函数形式,然后再确定平移方向和平移距离.
课堂精炼
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
数 学
题型三 三角函数图象的伸缩变换
知识梳理
ω(ω>0)对函数y=sin(ωx+φ)图象的影响
课堂精讲
课堂精讲
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂精炼
课堂精炼
课堂小结
1.通过本节课的学习,重点提升直观想象、逻辑推理、数学抽象素养.
2.由y=sin x的图象,通过变换可得到函数y=Asin(ωx+φ)(A>0,ω>0)的图象,其变化途径有两种:
注意:两种途径的变换顺序不同,其中变换的量也有所不同,这是易出错的地方,应特别注意.
数 学
数 学
题型一 “五点法”作函数y=Asin(ωx+φ)的图象
知识梳理
用“五点法”作函数y=Asin(ωx+φ)的图象关键是抓住五个关键点,即三个“平衡点”(即ωx+φ分别取0,π,2π时x所对应的点) 、一个“波峰点”、一个“波谷点”.
课堂精讲
课堂精讲
课堂精讲
课堂精讲
数 学
题型二 三角函数图象的平移变换
知识梳理
1.φ对函数y=sin(x+φ),x∈R的图象的影响
;
2. φ 对函数y=sin(ωx+φ) ,(ω>0)图象的影响
y=sinωx
的图象
φ>0时向左
y=sin(ωx+φ) 图象
φ<0时向右
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
课堂精讲
三角函数图象平移变换问题的分类及策略
(1)确定函数y=sin x的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
(2)已知两个函数解析式判断其图象间的平移关系时,首先要将解析式化为同名三角函数形式,然后再确定平移方向和平移距离.
课堂精炼
确定函数的图象经过变换后图象对应的解析式,关键是明确左右平移的方向,按“左加右减”的原则进行.
数 学
题型三 三角函数图象的伸缩变换
知识梳理
ω(ω>0)对函数y=sin(ωx+φ)图象的影响
课堂精讲
课堂精讲
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂精炼
课堂精炼
课堂小结
1.通过本节课的学习,重点提升直观想象、逻辑推理、数学抽象素养.
2.由y=sin x的图象,通过变换可得到函数y=Asin(ωx+φ)(A>0,ω>0)的图象,其变化途径有两种:
注意:两种途径的变换顺序不同,其中变换的量也有所不同,这是易出错的地方,应特别注意.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
