1.1 集合的概念 第二课时-高中数学人教A版必修一同步 课件(共21张PPT)
文档属性
| 名称 | 1.1 集合的概念 第二课时-高中数学人教A版必修一同步 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 19.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 06:08:32 | ||
图片预览



文档简介
(共21张PPT)
数 学
数 学
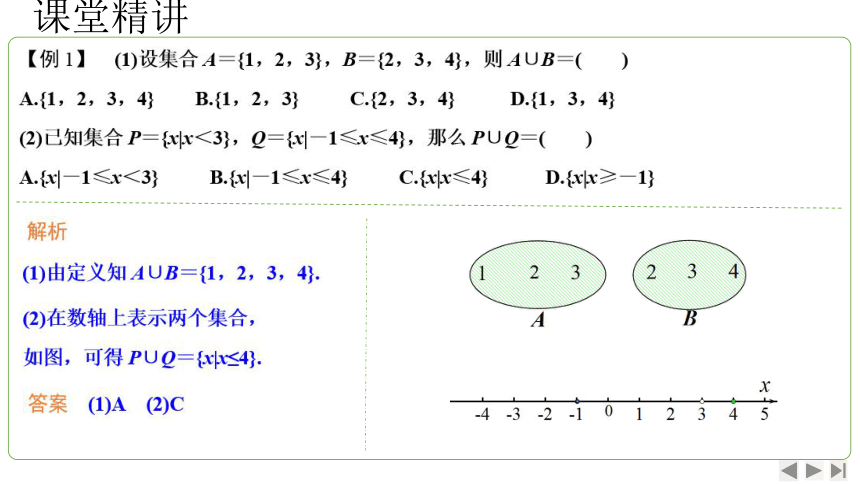
题型一 并集的概念及简单应用
知识梳理
课堂精讲
课堂精讲
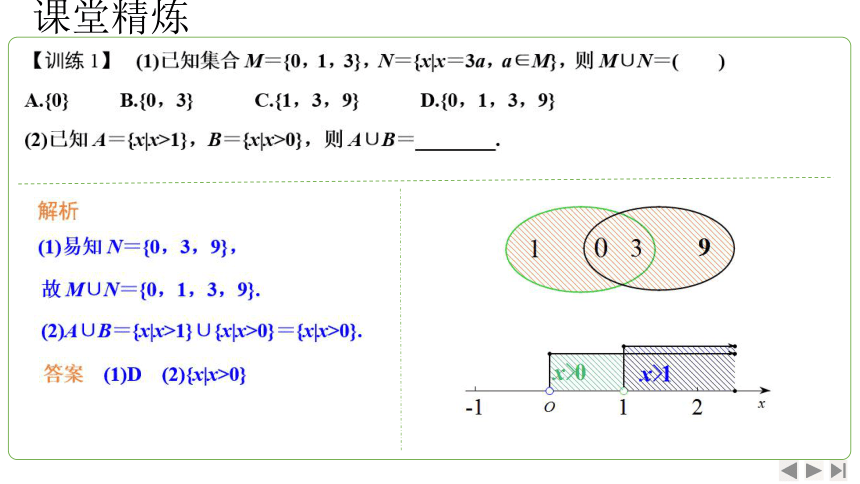
课堂精炼
数 学
题型二 交集的概念及简单应用
知识梳理
且
交集
{x|x∈A且x∈B}
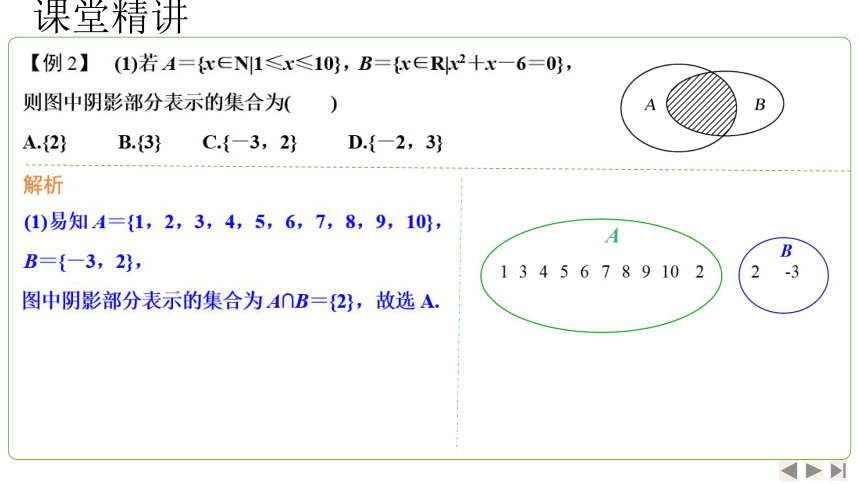
课堂精讲
课堂精讲
课堂精讲
课堂精炼
注意:
不要出现
M∩N
={x=3,y=-1}
的错误
数 学
题型三 并集、交集的运算性质及应用
知识梳理
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂小结
课堂小结
2
1孤度
0
A
X
学
等
23
234
A
B
A
B
求集合A∩B的常见类型
(1)若A,B的元素是方程的根,则应先解方程求出方程的根后,再求两集合的交
集.
(2)若A,B的元素是有序数对,则A∩B是指两个方程组成的方程组的解集,交
集是点集
3)若A,B是无限数集,可以利用数轴来求解,但要注意利用数轴表示不等式时,
含有端点的值用实心点表示,不含有端点的值用空心圈表示.
fx)=x2-3x+2
-5-4-3-2-10234567
-1
a=1.00
y=x2+2(a-1)+d25
a=0.20
2月01234§67
X
1.通过对并集、交集概念的理解,培养数学抽象素养,通过进行集合间的并集、
交集的运算提升数学运算素养
2.对并集、交集概念的理解
()对于并集,要注意其中“或”的意义,“或”与通常所说的“非此即彼”有原
则性的区别,它们是“相容”的.“x∈A或x∈B”这一条件,包括下列三种情况:
x∈A但xB;x∈B但xtA;x∈A且x∈B.因此,AUB是由所有至少属于A,B
两者之一的元素组成的集合.
(2)A∩B中的元素是“所有”属于集合A且属于集合B的元素,而不是部分,特
别地,当集合A和集合B没有公共元素时,不能说A与B没有交集,而是A∩B
数 学
数 学
题型一 并集的概念及简单应用
知识梳理
课堂精讲
课堂精讲
课堂精炼
数 学
题型二 交集的概念及简单应用
知识梳理
且
交集
{x|x∈A且x∈B}
课堂精讲
课堂精讲
课堂精讲
课堂精炼
注意:
不要出现
M∩N
={x=3,y=-1}
的错误
数 学
题型三 并集、交集的运算性质及应用
知识梳理
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂小结
课堂小结
2
1孤度
0
A
X
学
等
23
234
A
B
A
B
求集合A∩B的常见类型
(1)若A,B的元素是方程的根,则应先解方程求出方程的根后,再求两集合的交
集.
(2)若A,B的元素是有序数对,则A∩B是指两个方程组成的方程组的解集,交
集是点集
3)若A,B是无限数集,可以利用数轴来求解,但要注意利用数轴表示不等式时,
含有端点的值用实心点表示,不含有端点的值用空心圈表示.
fx)=x2-3x+2
-5-4-3-2-10234567
-1
a=1.00
y=x2+2(a-1)+d25
a=0.20
2月01234§67
X
1.通过对并集、交集概念的理解,培养数学抽象素养,通过进行集合间的并集、
交集的运算提升数学运算素养
2.对并集、交集概念的理解
()对于并集,要注意其中“或”的意义,“或”与通常所说的“非此即彼”有原
则性的区别,它们是“相容”的.“x∈A或x∈B”这一条件,包括下列三种情况:
x∈A但xB;x∈B但xtA;x∈A且x∈B.因此,AUB是由所有至少属于A,B
两者之一的元素组成的集合.
(2)A∩B中的元素是“所有”属于集合A且属于集合B的元素,而不是部分,特
别地,当集合A和集合B没有公共元素时,不能说A与B没有交集,而是A∩B
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
