1.4.2 充要条件课件-高中数学人教A版必修一同步 课件(共27张PPT)
文档属性
| 名称 | 1.4.2 充要条件课件-高中数学人教A版必修一同步 课件(共27张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 16.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 06:10:16 | ||
图片预览







文档简介
(共27张PPT)
数 学
数 学
题型一 充要条件的判断与探求
知识梳理
课堂精讲
课堂精讲
r
p
q
s
判断条件的关系,一定要从正反两方面进行判断,才能得出准确的结论。
课堂精讲
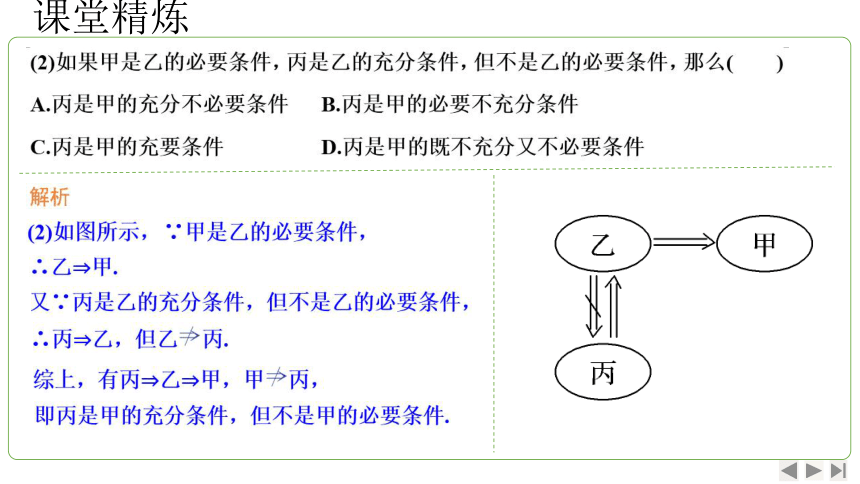
课堂精炼
课堂精炼
课堂精炼
数 学
题型二 充要条件的证明
知识梳理
课堂精讲
课堂精讲
课堂精炼
数 学
题型三 充要条件的应用
知识梳理
课堂精讲
因为p≠q,所以一定注意端点的控制
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂小结
知识梳理
课堂精讲
课堂精讲
课堂精炼
2
1孤度
0
A
X
等
1.逆命题
将命题“若p,则q”中的条件p和结论q互换,就得到一个新的命题
”,称这个命题为原命题的逆命题
2.充要条件
理解概念时要联系充分条件与必要条件的概念
如果“若p,则q”和它的逆命题“若q,则p”均是
即既有p→q,又
有q→p,就记作
此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,
简称为
显然,如果p是q的充要条件,那么q也是p的充要条件
角度1定义法判断条件间的关系
【例1-1
判断下列各题中,卫是否为q的充要条件?
(1)在△ABC中,p:∠A∠B,q:BC>AC:
(2)若a,b∈R,p:a2+b2=0,q:M=b=0;
(3)p:xp3,4:x2>9.
判断充分条件、必要条件及充要条件的四种方法
(1)定义法:直接判断若卫,则q”以及“若q,则p”的真假.
(2)集合法:即利用集合的包含关系判断.
(3)等价法:即利用p→q与q→p的等价关系,对于条件和结论是否定形式的命题,
一般运用等价法.
(4)传递法:充分条件和必要条件具有传递性,即由p1→p2→..→p,可得p1→p
充要条件也有传递性.
乙
甲
丙
1.充要条件的判断有三种方法:
2.充要条件的证明与探求
(1)充要条件的证明分充分性和必要性的证明在证明时要注意两种叙述方式的区
别:
①p是q的充要条件,则由p→q证的是
由q→卫证的是
②p的充要条件是q则p→1证的是必要性,由q→p证的是充分性.
(2)探求充要条件,可先求出必要条件,再证充分性;如果能保证每一步的变形转
化过程都可逆,也可以直接求出充要条件.
1、根据充分条件、必要条件求参数范围时,把问题转化为集合之间的包含关系,
通过集合之间的包含关系确定参数范围,但要注意转化的准确性.
2、“文氏”图的应用.
设有命题“若p则q”,记p所考察的对象的全体为集合A4g所考察的对象的
全体为集合B(其中A,B都是非空集合),则:
①若AB,则p是q的
②若BA,则p是q的
③若A=B,则p是q的
④若A∩B=p或A,B不相互包含,
则p是q的
数 学
数 学
题型一 充要条件的判断与探求
知识梳理
课堂精讲
课堂精讲
r
p
q
s
判断条件的关系,一定要从正反两方面进行判断,才能得出准确的结论。
课堂精讲
课堂精炼
课堂精炼
课堂精炼
数 学
题型二 充要条件的证明
知识梳理
课堂精讲
课堂精讲
课堂精炼
数 学
题型三 充要条件的应用
知识梳理
课堂精讲
因为p≠q,所以一定注意端点的控制
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂小结
知识梳理
课堂精讲
课堂精讲
课堂精炼
2
1孤度
0
A
X
等
1.逆命题
将命题“若p,则q”中的条件p和结论q互换,就得到一个新的命题
”,称这个命题为原命题的逆命题
2.充要条件
理解概念时要联系充分条件与必要条件的概念
如果“若p,则q”和它的逆命题“若q,则p”均是
即既有p→q,又
有q→p,就记作
此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,
简称为
显然,如果p是q的充要条件,那么q也是p的充要条件
角度1定义法判断条件间的关系
【例1-1
判断下列各题中,卫是否为q的充要条件?
(1)在△ABC中,p:∠A∠B,q:BC>AC:
(2)若a,b∈R,p:a2+b2=0,q:M=b=0;
(3)p:xp3,4:x2>9.
判断充分条件、必要条件及充要条件的四种方法
(1)定义法:直接判断若卫,则q”以及“若q,则p”的真假.
(2)集合法:即利用集合的包含关系判断.
(3)等价法:即利用p→q与q→p的等价关系,对于条件和结论是否定形式的命题,
一般运用等价法.
(4)传递法:充分条件和必要条件具有传递性,即由p1→p2→..→p,可得p1→p
充要条件也有传递性.
乙
甲
丙
1.充要条件的判断有三种方法:
2.充要条件的证明与探求
(1)充要条件的证明分充分性和必要性的证明在证明时要注意两种叙述方式的区
别:
①p是q的充要条件,则由p→q证的是
由q→卫证的是
②p的充要条件是q则p→1证的是必要性,由q→p证的是充分性.
(2)探求充要条件,可先求出必要条件,再证充分性;如果能保证每一步的变形转
化过程都可逆,也可以直接求出充要条件.
1、根据充分条件、必要条件求参数范围时,把问题转化为集合之间的包含关系,
通过集合之间的包含关系确定参数范围,但要注意转化的准确性.
2、“文氏”图的应用.
设有命题“若p则q”,记p所考察的对象的全体为集合A4g所考察的对象的
全体为集合B(其中A,B都是非空集合),则:
①若AB,则p是q的
②若BA,则p是q的
③若A=B,则p是q的
④若A∩B=p或A,B不相互包含,
则p是q的
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
