数学人教A版(2019)选择性必修第三册8.3.2独立性检验 课件(共35张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.3.2独立性检验 课件(共35张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 06:56:01 | ||
图片预览










文档简介
(共35张PPT)
8.3.2 独立性检验
第八章 成对数据的统计分析
(一)
创设情境
揭示课题
(二)
阅读精要
研讨新知
例题研讨
学习例题的正规表达
学习例题的常规方法
从例题中学会思考
如何看例题
小组互动
(三)
探索与发现
思考与感悟
(四)
归纳小结
回顾重点
(五)
作业布置
精炼双基
付出与回报
付出与回报
付出与回报
75%
55%
85%
属于不断付出与攀登的人
数学的美妙风景
OUTHT OF THED
0.430
表8.3-5
单位:人
疗效
疗法
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
21
115
136
表8.3-6
单位:人
肺癌
吸烟
合计
非肺癌患者
肺癌患者
非吸烟者
7775
42
7817
吸烟者
2099
49
2148
合计
9874
91
9965
昵图网nipic.com/风之雨
昵图网山uw.nipic.comY:sdoublEye
N0:201205070854322631B1
练习(第134页)
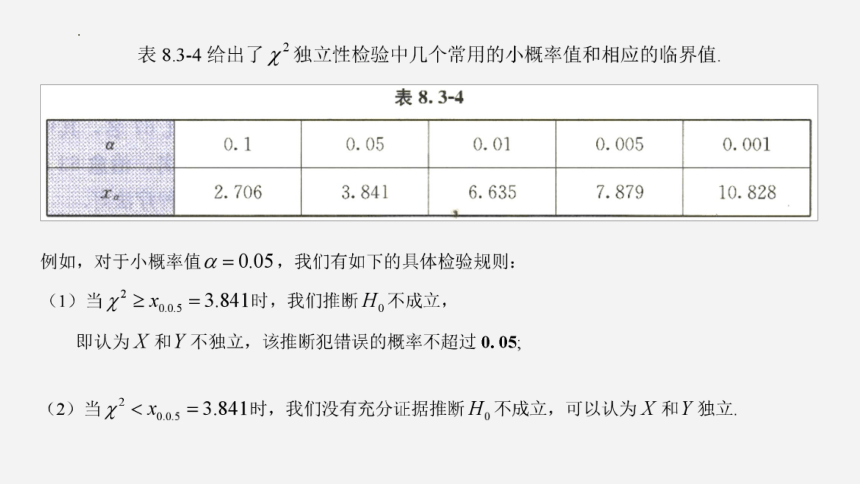
1.根据题意,X2=4.881>3.841=xo.5·依据小概率值a=0.05的独立性检验,我们推断
H。不成立,即可以认为两种疗法的效果有差异,该推断犯错误的概率不超过0.05.
甲种疗法未治愈和治愈的频率分别是号≈0.24和号0.76,乙种疗法未治愈和治愈的频
52
率分别是品≈0.087和8≈0.913,因此可以推断乙种疗法的效果比甲种疗法好。
,63
2.可能会得出不同的结论.对同一抽样数据,计算出来的X2的值是确定的.在独立性检验
中,基于不同的小概率值α的检验规则,对应不同的临界值x。,其与X2的大小关系可能不同,
相当于检验的标准发生变化,因此结论可能会不同.
3.零假设为H。:药物A与预防疾病B无关联,即药物A对预防疾病B没有效果.
根据列
联表中的数据,经计算得到x:=105X(29X1415×47)2
≈1.587<3.841=x0.o5.根据a=0.05
44×61×76×29
的独立性检验,没有充分证据推断H。不成立.因此可以认为药物A对预防疾病B没有效果,
4.零假设为H。:数学成绩与语文成绩独立,即数学成绩与语文成绩没有关联.根据列联表
中的数据,经计算得到x:=400×(212×73-61X54)2
273×127×266×134
≈48.034>3.841=x0.05.根据a=0.05的
独立性检验,我们可以推断H。不成立,即认为数学成绩与语文成绩有关联,该推断犯错误的概
率不超过0.05.
21
数学成绩不优秀的人中语文成绩不优秀和优秀的频率分别为
73
≈0.78
273≈0.22;数学
61
54
73
成绩优秀的人中语文成绩不优秀和优秀的频率分别为27≈0.43和127≈0.57.由此可以看出,数
学成绩优秀的人中语文成绩优秀的频率明显高于数学成绩不优秀的人中语文成绩优秀的频率.根
据频率稳定于概率的原理,我们可以推断,数学成绩优秀的人其语文成绩优秀的概率较大,
8.3.2 独立性检验
第八章 成对数据的统计分析
(一)
创设情境
揭示课题
(二)
阅读精要
研讨新知
例题研讨
学习例题的正规表达
学习例题的常规方法
从例题中学会思考
如何看例题
小组互动
(三)
探索与发现
思考与感悟
(四)
归纳小结
回顾重点
(五)
作业布置
精炼双基
付出与回报
付出与回报
付出与回报
75%
55%
85%
属于不断付出与攀登的人
数学的美妙风景
OUTHT OF THED
0.430
表8.3-5
单位:人
疗效
疗法
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
21
115
136
表8.3-6
单位:人
肺癌
吸烟
合计
非肺癌患者
肺癌患者
非吸烟者
7775
42
7817
吸烟者
2099
49
2148
合计
9874
91
9965
昵图网nipic.com/风之雨
昵图网山uw.nipic.comY:sdoublEye
N0:201205070854322631B1
练习(第134页)
1.根据题意,X2=4.881>3.841=xo.5·依据小概率值a=0.05的独立性检验,我们推断
H。不成立,即可以认为两种疗法的效果有差异,该推断犯错误的概率不超过0.05.
甲种疗法未治愈和治愈的频率分别是号≈0.24和号0.76,乙种疗法未治愈和治愈的频
52
率分别是品≈0.087和8≈0.913,因此可以推断乙种疗法的效果比甲种疗法好。
,63
2.可能会得出不同的结论.对同一抽样数据,计算出来的X2的值是确定的.在独立性检验
中,基于不同的小概率值α的检验规则,对应不同的临界值x。,其与X2的大小关系可能不同,
相当于检验的标准发生变化,因此结论可能会不同.
3.零假设为H。:药物A与预防疾病B无关联,即药物A对预防疾病B没有效果.
根据列
联表中的数据,经计算得到x:=105X(29X1415×47)2
≈1.587<3.841=x0.o5.根据a=0.05
44×61×76×29
的独立性检验,没有充分证据推断H。不成立.因此可以认为药物A对预防疾病B没有效果,
4.零假设为H。:数学成绩与语文成绩独立,即数学成绩与语文成绩没有关联.根据列联表
中的数据,经计算得到x:=400×(212×73-61X54)2
273×127×266×134
≈48.034>3.841=x0.05.根据a=0.05的
独立性检验,我们可以推断H。不成立,即认为数学成绩与语文成绩有关联,该推断犯错误的概
率不超过0.05.
21
数学成绩不优秀的人中语文成绩不优秀和优秀的频率分别为
73
≈0.78
273≈0.22;数学
61
54
73
成绩优秀的人中语文成绩不优秀和优秀的频率分别为27≈0.43和127≈0.57.由此可以看出,数
学成绩优秀的人中语文成绩优秀的频率明显高于数学成绩不优秀的人中语文成绩优秀的频率.根
据频率稳定于概率的原理,我们可以推断,数学成绩优秀的人其语文成绩优秀的概率较大,
