11.4 解一元一次不等式-苏科版数学七年级下册同步课件(共16张PPT)
文档属性
| 名称 | 11.4 解一元一次不等式-苏科版数学七年级下册同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 21:03:19 | ||
图片预览






文档简介
(共16张PPT)
11.4 解一元一次不等式
第11章 二元一次不等式
一元一次不等式的定义
一元一次不等式的解法
知识点
一元一次不等式的定义
1
1.定义 只含有一个未知数,并且未知数的次数都是1,系数不等于0,像这样的不等式,叫做一元一次不等式.
判断条件:(1)都是整式;(2)只含一个未知数;(3)未知数的次数是1;(4)未知数的系数不为0.
特别警示:
判断一个不等式是否为一元一次不等式,必须化简整理后再判断,如果化简后不等号的两边都是整式且只含一个未知数,未知数的次数为1 且系数不为0,那么此不等式为一元一次不等式.
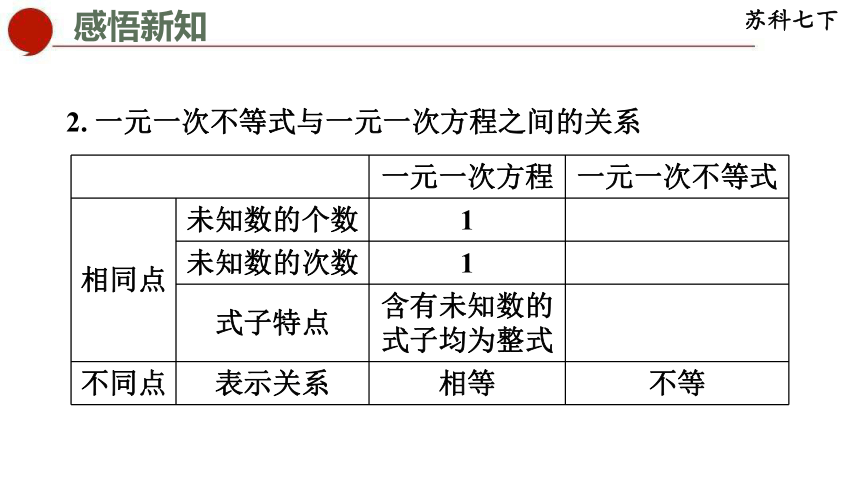
2. 一元一次不等式与一元一次方程之间的关系
一元一次方程 一元一次不等式
相同点 未知数的个数 1
未知数的次数 1
式子特点 含有未知数的式子均为整式
不同点 表示关系 相等 不等
[ 期末·苏州] 下列不等式中,属于一元一次不等式的
是( )
A.x+y ≥ 0 B.x+2<48
C.x2>1 D.≤ 5
B
解题秘方:紧扣一元一次不等式的判断条件进行选择即可.
真题1
方法点拨:
判断一个不等式是否为一元一次不等式的步骤:
先对所给不等式进行化简整理,再看是否满足一元一次不等式的判断条件,同时要注意:
(1)化简前不等式的左右两边都是整式;
(2)化简后未知数的次数是1 且系数不为0 .
▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲
解:选项A 中,含有两个未知数,故此选项不符合题意;
选项B 中,将不等式化简,整理为x < 46,符合一元一次不等式的定义,故此选项符合题意;
选项C 中,未知数的最高次数为2,故此选项不符合题意;
选项D 中,分母含未知数,不是整式,故此选项不符合题意.
知识点
一元一次不等式的解法
2
1. 解一元一次不等式的一般步骤
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.解一元一次不等式,要根据不等式的基本性质,将不等式逐步化为 “x > a(x ≥ a)”或“x < a(x ≤ a)”的最简形式.
特别提醒:
解一元一次不等式时,五个步骤不一定都要用到,并且不一定都要按照这个顺序求解,应根据不等式的特点灵活运用.
2. 解一元一次不等式与解一元一次方程的区别与联系
一元一次方程 一元一次不等式
解法步骤 ①去分母;②去括号;③移项;④合并同类项;⑤系数化为1(解不等式:去分母、系数化为1 时,若两边同时乘(或除以)一个负数,则不等号的方向改变)
依据 等式的基本性质 不等式的基本性质
解的个数 只有一个解 有无数多个解
解(集)的形式 x = a x < a(x ≤ a)或x > a(x ≥ a)
例1
解不等式:14-2x≥ 6,并把解集在数轴上表示出来.
解题秘方:先根据解一元一次不等式的一般步骤求出解集,然后在数轴上表示出解集.
解:解不等式:14-2x> 6
移项,得-2x > 6-14.
合并同类项,得-3x > -8.
根据不等式的性质2,在不等式的两边都除以-2,
得x <4.
这个不等式的解集在数轴上的表示如图11-6 所示.
注意改变不等号的方向.
例 2
解不等式2x-1≥ ,并把它的解集在数轴上表示出来.
x为未知数.
解:根据不等式的性质2,在不等式的两边都乘2,得 2(2x-1)≥3x-1.
去括号,得4x-2 ≥3x-1.
移项,得4x-3x ≥-1+2.
合并同类项,得 x≥1.
这个不等式的解集在数轴上表示如下(图11-7):
解一元一次不等式
一元一次
不等式
不等式
解法
解集表示
定义
去分母,去括号,移项,
合并同类项,系数化为1.
用数轴表示
11.4 解一元一次不等式
第11章 二元一次不等式
一元一次不等式的定义
一元一次不等式的解法
知识点
一元一次不等式的定义
1
1.定义 只含有一个未知数,并且未知数的次数都是1,系数不等于0,像这样的不等式,叫做一元一次不等式.
判断条件:(1)都是整式;(2)只含一个未知数;(3)未知数的次数是1;(4)未知数的系数不为0.
特别警示:
判断一个不等式是否为一元一次不等式,必须化简整理后再判断,如果化简后不等号的两边都是整式且只含一个未知数,未知数的次数为1 且系数不为0,那么此不等式为一元一次不等式.
2. 一元一次不等式与一元一次方程之间的关系
一元一次方程 一元一次不等式
相同点 未知数的个数 1
未知数的次数 1
式子特点 含有未知数的式子均为整式
不同点 表示关系 相等 不等
[ 期末·苏州] 下列不等式中,属于一元一次不等式的
是( )
A.x+y ≥ 0 B.x+2<48
C.x2>1 D.≤ 5
B
解题秘方:紧扣一元一次不等式的判断条件进行选择即可.
真题1
方法点拨:
判断一个不等式是否为一元一次不等式的步骤:
先对所给不等式进行化简整理,再看是否满足一元一次不等式的判断条件,同时要注意:
(1)化简前不等式的左右两边都是整式;
(2)化简后未知数的次数是1 且系数不为0 .
▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲ ▲
解:选项A 中,含有两个未知数,故此选项不符合题意;
选项B 中,将不等式化简,整理为x < 46,符合一元一次不等式的定义,故此选项符合题意;
选项C 中,未知数的最高次数为2,故此选项不符合题意;
选项D 中,分母含未知数,不是整式,故此选项不符合题意.
知识点
一元一次不等式的解法
2
1. 解一元一次不等式的一般步骤
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.解一元一次不等式,要根据不等式的基本性质,将不等式逐步化为 “x > a(x ≥ a)”或“x < a(x ≤ a)”的最简形式.
特别提醒:
解一元一次不等式时,五个步骤不一定都要用到,并且不一定都要按照这个顺序求解,应根据不等式的特点灵活运用.
2. 解一元一次不等式与解一元一次方程的区别与联系
一元一次方程 一元一次不等式
解法步骤 ①去分母;②去括号;③移项;④合并同类项;⑤系数化为1(解不等式:去分母、系数化为1 时,若两边同时乘(或除以)一个负数,则不等号的方向改变)
依据 等式的基本性质 不等式的基本性质
解的个数 只有一个解 有无数多个解
解(集)的形式 x = a x < a(x ≤ a)或x > a(x ≥ a)
例1
解不等式:14-2x≥ 6,并把解集在数轴上表示出来.
解题秘方:先根据解一元一次不等式的一般步骤求出解集,然后在数轴上表示出解集.
解:解不等式:14-2x> 6
移项,得-2x > 6-14.
合并同类项,得-3x > -8.
根据不等式的性质2,在不等式的两边都除以-2,
得x <4.
这个不等式的解集在数轴上的表示如图11-6 所示.
注意改变不等号的方向.
例 2
解不等式2x-1≥ ,并把它的解集在数轴上表示出来.
x为未知数.
解:根据不等式的性质2,在不等式的两边都乘2,得 2(2x-1)≥3x-1.
去括号,得4x-2 ≥3x-1.
移项,得4x-3x ≥-1+2.
合并同类项,得 x≥1.
这个不等式的解集在数轴上表示如下(图11-7):
解一元一次不等式
一元一次
不等式
不等式
解法
解集表示
定义
去分母,去括号,移项,
合并同类项,系数化为1.
用数轴表示
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
