7.4 认识三角形-苏科版数学七年级下册同步课件(共45张PPT)
文档属性
| 名称 | 7.4 认识三角形-苏科版数学七年级下册同步课件(共45张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 21:58:23 | ||
图片预览










文档简介
(共45张PPT)
第7章 平面图形的认识(二)
7.4 认识三角形
三角形的定义及相关元素的定义
三角形的分类
三角形的三边关系
三角形的角平分线、中线、高
知识点
三角形的定义及相关元素的定义
1
1. 三角形的定义 三角形是由3 条不在同一条直线上的线段,首尾依次相接组成的图形.
● ● ● ● ● ● ● ●
● ● ● ●
特别解读:
1. 三角形的“三要素”:
(1)三条线段;
(2) 三个顶点不在同一条直线上;
(3) 三条线段首尾依次相接.
2. 三角形的边是线段,既可以用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示,如顶点A 所对的边BC 可以用a 表示.
▲ ▲
三角形的表示方法:用符号“ △” 表示三角形, 如图7.4-1, 顶点是A、B、C 的三角形记作“△ ABC”,读作“三角形ABC”.
字母的顺序可以自由安排.
2. 三角形的“三元素”
(1)顶点:三角形相邻两边的公共端点叫做三角形的顶点. 如图7.4-1,点A、B、C 是△ ABC 的三个顶点.
(2)边:组成三角形的线段叫做三角形的边. 如图7.4-1,线段AB、BC、AC 是△ ABC 的三条边.
(3)内角:在三角形中,相邻两边所组成的角叫做三角形的内角,简称三角形的角. 如图7.4-1,∠ A、∠ B、∠ C 是△ ABC 的三个角.
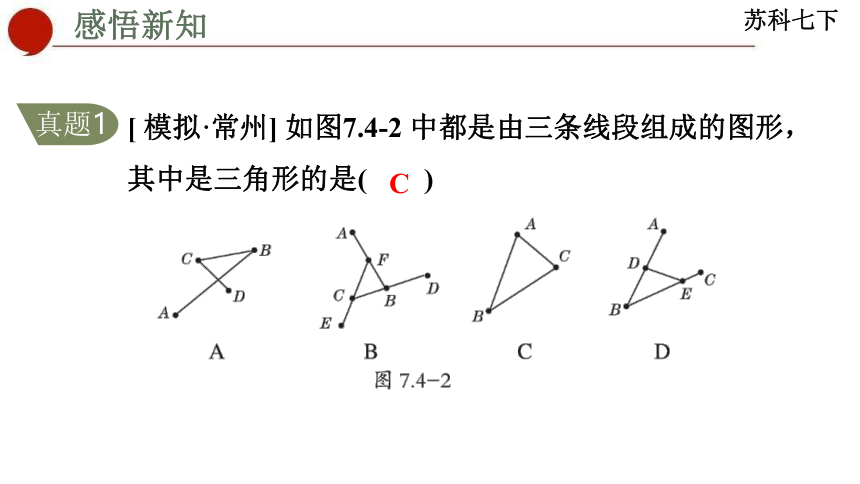
[ 模拟·常州] 如图7.4-2 中都是由三条线段组成的图形,
其中是三角形的是( )
C
真题1
解题秘方:紧扣三角形的“三要素”进行识别.
解:选项A、B、C、D 都是由三条线段组成的图形,但选项A、B、D不是首尾顺次相接的,只有选项C 符合三角形的“三要素”.
特别提醒:
图形是三角形表示整个图形是一个三角形,图形内含有三角形表示图形局部有三角形,如选项A、B、D 中的图形内都含有三角形,但整个图形不是三角形.
知识点
三角形的分类
2
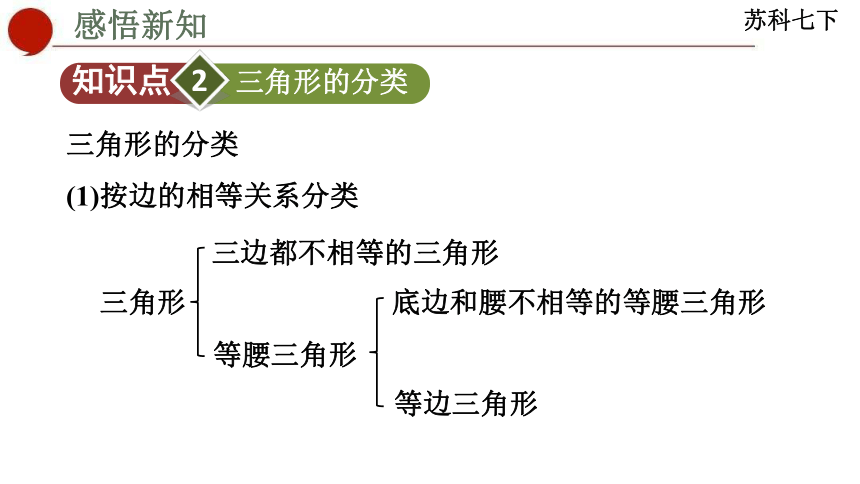
三角形的分类
(1)按边的相等关系分类
三角形
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
等腰三角形包括等边三角形,等边三角形是特殊的等腰三角形.
分类示意图如图7.4-3 所示.
(2)按内角的大小分类
三角形
锐角三角形
直角三角形
钝角三角形
分类示意图如图7.4-4 所示.
特别提醒:
三角形按内角的大小分类和按边的相等关系分类是两种不同的分类方式,各自独立,但无论按哪种标准分类,原则都是不重不漏.
对于等腰直角三角形,按边的相等关系分类属于等腰三角形,按内角的大小分类属于直角三角形.
▲ ▲ ▲ ▲
例2
根据下列所给条件,判断△ ABC 的形状:
(1)∠ A=45°,∠ B=65°,∠ C=70°;
解:因为∠ A=45°,∠ B=65°,∠ C=70°,
所以∠ A <∠ B <∠ C < 90° .
所以△ ABC 是锐角三角形.
(2)∠ C=120°;
(3)∠ C=90° .
解:因为∠ C=120°> 90°,所以△ ABC 是钝角三角形.
因为∠ C=90°,所以△ ABC 是直角三角形.
解题秘方:根据三角形的内角的大小进行判断.
方法技巧:
确定三角形的分类标准方法:
1. 若按角分类,则看这个三角形的最大角的类型:最大角是钝角的三角形是钝角三角形;最大角是直角的三角形是直角三角形;最大角是锐角的三角形是锐角三角形.
2. 若按边分类,则看边是否相等.
▲ ▲ ▲ ▲ ▲ ▲
▲ ▲ ▲ ▲ ▲ ▲
[ 模拟·连云港] 已知△ ABC 的三边长分别为a、b、c,试判断△ ABC 的形状.
(1)三边长满足(a-b)2+ | b-c | =0;
解:因为(a-b)2+ | b-c | =0,
所以a-b=0 且b-c=0.所以a=b=c.
所以△ ABC 为等边三角形.
真题2
(2)三边长满足(a-b)(b-c)=0.
解:因为(a-b)(b-c)=0,
所以a-b=0 或b-c=0.
所以a=b 或b=c.
所以△ ABC 为等腰三角形.
解题秘方:要判断三角形的形状,可根据“边是否相等”来判断,所以从条件中分析出三边长的关系是解决本题的关键.
“a=b 且b=c”与“a=b或b=c”得到的结论是不一样的.
方法点拨:
从边的角度判断三角形的形状,若只能判定两条边相等,则此三角形是等腰三角形,若能判定三边相等,则此三角形是等边三角形.
知识点
三角形的三边关系
3
三角形的三边关系 三角形的任意两边之和大于第三边.
我们可以从不同的角度理解,列表如下:
文字语言 表达方式 理论依据 图形
三角形的任意两边之和大于第三边 a+b>c,b+c>a,a+c>b 两点之间线段最短
三角形的任意两边之差小于第三边 a-ba-cb>c)
2. 三角形三边关系的应用
(1)判断三条线段能否组成三角形;
(2)已知三角形的两边长,确定第三边长(或周长)的取值范围;
(3)当三角形的边长用字母表示时,求字母的取值范围;
(4)证明线段的不等关系.
特别提醒:
●三角形中的“两边”指任意两边,应用时常选取两条较小的边的和与第三边作比较,选取最大边与最小边的差与第三边作比较.
●已知三角形两边长分别为a、b(a>b), 根据三角形的三边关系可知,第三边长c 的取值范围是a-b[ 期中·徐州] 下列各组线段能组成一个三角形的是( )
A.2 cm、3 cm、6 cm
B.6 cm、8 cm、10 cm
C.5 cm、5 cm、10 cm
D.4 cm、6 cm、10 cm
B
真题3
解题秘方:紧扣“三角形的三边关系”进行判断.
解:A 选项中,因为2+3 < 6,即两边之和小于第三边,所以不能组成三角形;B 选项中,因为6+8 = 14 > 10,即两边之和大于第三边,所以能组成三角形;C 选项中,因为5+5 = 10,即两边之和等于第三边,所以不能组成三角形;D 选项中,因为4+6 = 10,即两边之和等于第三边,所以不能组成三角形.
技巧提醒:
确定三条线段能否组成三角形的两种方法:
1. 看较短的两条线段的和是否大于最长的线段,若是,则能组成三角形;反之, 则不能组成三角形.
2. 看最长的线段减去最短的线段的差是否小于第三条线段,若是,则能组成三角形;反之,则不能组成三角形.
知识点
三角形的角平分线、中线、高
4
1. 三角形的角平分线、中线和高是三角形中的三种重要线段,它们是研究三角形的一些特征的基础,我们需要从不同的角度进行理解,列表如下:
三角形的中线 三角形的角平分线 三角形的高
文字语言 在三角形中,连接一个顶点与它的对边中点的线段 在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段 从三角形的一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段
图形语言
三角形的中线 三角形的角平分线 三角形的高
注意事项 在三角形的
内部 (1)与角的平分线不同
(2)在三角形的内部 (1)与边的垂线不同
(2)不一定在三角形的内部
重要特征 一个三角形有三条中线,它们相交于三角形内一点 一个三角形有三条角平分线,它们相交于三角形内一点 三角形的三条高所在的直线相交于一点
● ●
● ● ●
● ● ● ●
● ●
● ● ● ● ● ●
● ●
● ● ● ● ● ●
●
特别解读:
三角形的中线把三角形分成的两个三角形的面积和周长的关系:
1. 两个三角形的面积相等;
2. 两个三角形的周长的差等于这两个三角形另两边的差.
特别提醒:
●角的平分线是一条射线,而三角形的角平分线是一条线段.
●三角形的角平分线是其内角的平分线的一部分,故角的平分线的性质三角形的角平分线都具有.
示图:
2. 三角形中三个重要的点
三条高所在直线的交点叫垂心, 三条中线的交点叫重心, 三条角平分线的交点叫内心.
[ 月考· 江阴] 如图7.4-8,已知AD 为△ ABC 的中线,
AB = 12 cm,AC = 9 cm,△ ACD 的周长为27 cm,则△ ABD 的周长为________cm.
30
真题4
解题秘方:紧扣中线将三角形分成的两个三角形的周长之间的关系解题.
方法点拨:
解答有关三角形中线的周长问题,需要熟记三角形中线的定义,并能把周长问题转化为线段问题. 由所给出的三角形周长和相关线段的长作为出发点,挖掘两个三角形公共边之间的关系,借助中线,可求得待求边或边长之和的长.
解:因为△ ACD 的周长为27 cm,AC = 9 cm,
所以AC+DC+AD = 27 cm.即9+DC+AD = 27 cm.
所以AD+CD = 18 cm.
因为AD 为△ ABC 的中线,
所以BD = CD.所以AD+BD = 18 cm.
因为AB = 12 cm,所以AB+AD+BD = 30 cm,
即△ ABD 的周长为30 cm.
[ 期中·重庆] 如图7.4-9,已知在△ ABC 中,点D、E 分别是边BC、AB 的中点.若△ ABC 的面积等于8,则△ BDE 的面积等于( )
A.2
B.3
C.4
D.5
A
真题5
解题秘方:紧扣中线将三角形分成的两个三角形的面积之间的关系解题.
详解:
三角形的中线把边分成相等的两条线段,所以BD=CD且△ABD的边BD上的高与△ACD的边CD上的高相同,根据等底同高的三角形的面积相等,可得所分成的两个三角形的面积相等,
[ 模拟·江阴] 如图7.4-11 所示,在△ ABC 中,边AB 上的高线画法正确的是( )
B
真题6
解题秘方:紧扣“三角形的高”的定义进行识别.
解:A 选项中,AH 是边BC 上的高线;C 选项中,AH 不是边AB 上的高线,没有过顶点C;D 选项中,BH 是边AC 上的高线. 所以选项A、C、D都不符合题意.
特别提醒:
找三角形某边上的高的方法:
1. 找出该边所对的顶点.
2. 过此顶点作该边的垂线, 垂线段为该边上的高.
如:作△ ABC 中边BC 上的高→找边BC 所对的顶点A,过点A作BC 的垂线(E为垂足),垂线段AE即为边BC 上的高.
认识三角形
三角形
边
顶点
组成
元素
角
分类
按边分类
按角分类
三边关系
角平分线
顶点
高
第7章 平面图形的认识(二)
7.4 认识三角形
三角形的定义及相关元素的定义
三角形的分类
三角形的三边关系
三角形的角平分线、中线、高
知识点
三角形的定义及相关元素的定义
1
1. 三角形的定义 三角形是由3 条不在同一条直线上的线段,首尾依次相接组成的图形.
● ● ● ● ● ● ● ●
● ● ● ●
特别解读:
1. 三角形的“三要素”:
(1)三条线段;
(2) 三个顶点不在同一条直线上;
(3) 三条线段首尾依次相接.
2. 三角形的边是线段,既可以用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示,如顶点A 所对的边BC 可以用a 表示.
▲ ▲
三角形的表示方法:用符号“ △” 表示三角形, 如图7.4-1, 顶点是A、B、C 的三角形记作“△ ABC”,读作“三角形ABC”.
字母的顺序可以自由安排.
2. 三角形的“三元素”
(1)顶点:三角形相邻两边的公共端点叫做三角形的顶点. 如图7.4-1,点A、B、C 是△ ABC 的三个顶点.
(2)边:组成三角形的线段叫做三角形的边. 如图7.4-1,线段AB、BC、AC 是△ ABC 的三条边.
(3)内角:在三角形中,相邻两边所组成的角叫做三角形的内角,简称三角形的角. 如图7.4-1,∠ A、∠ B、∠ C 是△ ABC 的三个角.
[ 模拟·常州] 如图7.4-2 中都是由三条线段组成的图形,
其中是三角形的是( )
C
真题1
解题秘方:紧扣三角形的“三要素”进行识别.
解:选项A、B、C、D 都是由三条线段组成的图形,但选项A、B、D不是首尾顺次相接的,只有选项C 符合三角形的“三要素”.
特别提醒:
图形是三角形表示整个图形是一个三角形,图形内含有三角形表示图形局部有三角形,如选项A、B、D 中的图形内都含有三角形,但整个图形不是三角形.
知识点
三角形的分类
2
三角形的分类
(1)按边的相等关系分类
三角形
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
等腰三角形包括等边三角形,等边三角形是特殊的等腰三角形.
分类示意图如图7.4-3 所示.
(2)按内角的大小分类
三角形
锐角三角形
直角三角形
钝角三角形
分类示意图如图7.4-4 所示.
特别提醒:
三角形按内角的大小分类和按边的相等关系分类是两种不同的分类方式,各自独立,但无论按哪种标准分类,原则都是不重不漏.
对于等腰直角三角形,按边的相等关系分类属于等腰三角形,按内角的大小分类属于直角三角形.
▲ ▲ ▲ ▲
例2
根据下列所给条件,判断△ ABC 的形状:
(1)∠ A=45°,∠ B=65°,∠ C=70°;
解:因为∠ A=45°,∠ B=65°,∠ C=70°,
所以∠ A <∠ B <∠ C < 90° .
所以△ ABC 是锐角三角形.
(2)∠ C=120°;
(3)∠ C=90° .
解:因为∠ C=120°> 90°,所以△ ABC 是钝角三角形.
因为∠ C=90°,所以△ ABC 是直角三角形.
解题秘方:根据三角形的内角的大小进行判断.
方法技巧:
确定三角形的分类标准方法:
1. 若按角分类,则看这个三角形的最大角的类型:最大角是钝角的三角形是钝角三角形;最大角是直角的三角形是直角三角形;最大角是锐角的三角形是锐角三角形.
2. 若按边分类,则看边是否相等.
▲ ▲ ▲ ▲ ▲ ▲
▲ ▲ ▲ ▲ ▲ ▲
[ 模拟·连云港] 已知△ ABC 的三边长分别为a、b、c,试判断△ ABC 的形状.
(1)三边长满足(a-b)2+ | b-c | =0;
解:因为(a-b)2+ | b-c | =0,
所以a-b=0 且b-c=0.所以a=b=c.
所以△ ABC 为等边三角形.
真题2
(2)三边长满足(a-b)(b-c)=0.
解:因为(a-b)(b-c)=0,
所以a-b=0 或b-c=0.
所以a=b 或b=c.
所以△ ABC 为等腰三角形.
解题秘方:要判断三角形的形状,可根据“边是否相等”来判断,所以从条件中分析出三边长的关系是解决本题的关键.
“a=b 且b=c”与“a=b或b=c”得到的结论是不一样的.
方法点拨:
从边的角度判断三角形的形状,若只能判定两条边相等,则此三角形是等腰三角形,若能判定三边相等,则此三角形是等边三角形.
知识点
三角形的三边关系
3
三角形的三边关系 三角形的任意两边之和大于第三边.
我们可以从不同的角度理解,列表如下:
文字语言 表达方式 理论依据 图形
三角形的任意两边之和大于第三边 a+b>c,b+c>a,a+c>b 两点之间线段最短
三角形的任意两边之差小于第三边 a-b
2. 三角形三边关系的应用
(1)判断三条线段能否组成三角形;
(2)已知三角形的两边长,确定第三边长(或周长)的取值范围;
(3)当三角形的边长用字母表示时,求字母的取值范围;
(4)证明线段的不等关系.
特别提醒:
●三角形中的“两边”指任意两边,应用时常选取两条较小的边的和与第三边作比较,选取最大边与最小边的差与第三边作比较.
●已知三角形两边长分别为a、b(a>b), 根据三角形的三边关系可知,第三边长c 的取值范围是a-b
A.2 cm、3 cm、6 cm
B.6 cm、8 cm、10 cm
C.5 cm、5 cm、10 cm
D.4 cm、6 cm、10 cm
B
真题3
解题秘方:紧扣“三角形的三边关系”进行判断.
解:A 选项中,因为2+3 < 6,即两边之和小于第三边,所以不能组成三角形;B 选项中,因为6+8 = 14 > 10,即两边之和大于第三边,所以能组成三角形;C 选项中,因为5+5 = 10,即两边之和等于第三边,所以不能组成三角形;D 选项中,因为4+6 = 10,即两边之和等于第三边,所以不能组成三角形.
技巧提醒:
确定三条线段能否组成三角形的两种方法:
1. 看较短的两条线段的和是否大于最长的线段,若是,则能组成三角形;反之, 则不能组成三角形.
2. 看最长的线段减去最短的线段的差是否小于第三条线段,若是,则能组成三角形;反之,则不能组成三角形.
知识点
三角形的角平分线、中线、高
4
1. 三角形的角平分线、中线和高是三角形中的三种重要线段,它们是研究三角形的一些特征的基础,我们需要从不同的角度进行理解,列表如下:
三角形的中线 三角形的角平分线 三角形的高
文字语言 在三角形中,连接一个顶点与它的对边中点的线段 在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段 从三角形的一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段
图形语言
三角形的中线 三角形的角平分线 三角形的高
注意事项 在三角形的
内部 (1)与角的平分线不同
(2)在三角形的内部 (1)与边的垂线不同
(2)不一定在三角形的内部
重要特征 一个三角形有三条中线,它们相交于三角形内一点 一个三角形有三条角平分线,它们相交于三角形内一点 三角形的三条高所在的直线相交于一点
● ●
● ● ●
● ● ● ●
● ●
● ● ● ● ● ●
● ●
● ● ● ● ● ●
●
特别解读:
三角形的中线把三角形分成的两个三角形的面积和周长的关系:
1. 两个三角形的面积相等;
2. 两个三角形的周长的差等于这两个三角形另两边的差.
特别提醒:
●角的平分线是一条射线,而三角形的角平分线是一条线段.
●三角形的角平分线是其内角的平分线的一部分,故角的平分线的性质三角形的角平分线都具有.
示图:
2. 三角形中三个重要的点
三条高所在直线的交点叫垂心, 三条中线的交点叫重心, 三条角平分线的交点叫内心.
[ 月考· 江阴] 如图7.4-8,已知AD 为△ ABC 的中线,
AB = 12 cm,AC = 9 cm,△ ACD 的周长为27 cm,则△ ABD 的周长为________cm.
30
真题4
解题秘方:紧扣中线将三角形分成的两个三角形的周长之间的关系解题.
方法点拨:
解答有关三角形中线的周长问题,需要熟记三角形中线的定义,并能把周长问题转化为线段问题. 由所给出的三角形周长和相关线段的长作为出发点,挖掘两个三角形公共边之间的关系,借助中线,可求得待求边或边长之和的长.
解:因为△ ACD 的周长为27 cm,AC = 9 cm,
所以AC+DC+AD = 27 cm.即9+DC+AD = 27 cm.
所以AD+CD = 18 cm.
因为AD 为△ ABC 的中线,
所以BD = CD.所以AD+BD = 18 cm.
因为AB = 12 cm,所以AB+AD+BD = 30 cm,
即△ ABD 的周长为30 cm.
[ 期中·重庆] 如图7.4-9,已知在△ ABC 中,点D、E 分别是边BC、AB 的中点.若△ ABC 的面积等于8,则△ BDE 的面积等于( )
A.2
B.3
C.4
D.5
A
真题5
解题秘方:紧扣中线将三角形分成的两个三角形的面积之间的关系解题.
详解:
三角形的中线把边分成相等的两条线段,所以BD=CD且△ABD的边BD上的高与△ACD的边CD上的高相同,根据等底同高的三角形的面积相等,可得所分成的两个三角形的面积相等,
[ 模拟·江阴] 如图7.4-11 所示,在△ ABC 中,边AB 上的高线画法正确的是( )
B
真题6
解题秘方:紧扣“三角形的高”的定义进行识别.
解:A 选项中,AH 是边BC 上的高线;C 选项中,AH 不是边AB 上的高线,没有过顶点C;D 选项中,BH 是边AC 上的高线. 所以选项A、C、D都不符合题意.
特别提醒:
找三角形某边上的高的方法:
1. 找出该边所对的顶点.
2. 过此顶点作该边的垂线, 垂线段为该边上的高.
如:作△ ABC 中边BC 上的高→找边BC 所对的顶点A,过点A作BC 的垂线(E为垂足),垂线段AE即为边BC 上的高.
认识三角形
三角形
边
顶点
组成
元素
角
分类
按边分类
按角分类
三边关系
角平分线
顶点
高
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
