7.5 多边形的内角和与外角和-苏科版数学七年级下册同步课件(共34张PPT)
文档属性
| 名称 | 7.5 多边形的内角和与外角和-苏科版数学七年级下册同步课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
第7章 平面图形的认识(二)
7.5 多边形的内角和与外角和
三角形的内角和
多边形的内角和
多边形的外角和
知识点
三角形的内角和
1
1. 三角形的内角和 三角形的内角和是180° .
表达方式:在△ ABC 中,∠ A+ ∠ B+ ∠ C=180° .
特别解读:
1. 三角形的内角和是180°揭示了三角形三个内角之间的数量关系.
2. 三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角.
2. 说明“三角形的内角和是180°”的思路
思路一: 利用“两直线平行,内错角及同位角相等”将三角形的三个内角转化为一个平角,如图7.5-1 ①所示.
思路二: 利用“两直线平行,内错角相等”将三角形的三个内角转化为两平行线间的一组同旁内角,如图7.5-1 ②所示.
例 1
在△ ABC 中,∠A=40°,∠B= ∠C,求∠C的度数;
解: 在△ ABC中,
由∠ A+ ∠ B+ ∠ C=180°,∠ A=40°,得
∠ B+ ∠ C=180°- ∠ A=180°-40°=140°,
由∠B= ∠C,得
2∠ C=140°=70°.
解题秘方:紧扣三角形的内角和是180°建立方程求解.
方法点拨:
求三角形内角的度数的方法:
1. 若已知两个角的度数,求第三个角的度数,直接利用三角形的内角和定理求解.
2. 若已知一个角的度数及另两个角之间的等量关系,或不知道任何一个角的度数,只知道三个角之间的数量关系,一般根据“三角形内角和为180°”这个隐含的等量关系列方程求解.
[ 月考· 宜兴] 若一个三角形的三个内角度数的比为
2 ∶ 3 ∶ 4,则这个三角形是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
A
真题1
解题秘方:紧扣三角形的三个内角的度数比,求出三个内角的度数,根据三个内角的度数判断三角形的形状.
另解: 设三个内角分别为2x °、3x °、4x °,
则2x+3x+4x=180. 解得x=20.所以4x = 80. 即可求解.
方法点拨:
按角判断一个三角形的形状的方法:
可以将三个角的度数分别求出;也可以看三角形中最大的角的大小:最大角是锐角,三角形就是锐角三角形;最大角是直角,三角形就是直角三角形;最大角是钝角,三角形就是钝角三角形.
例 2
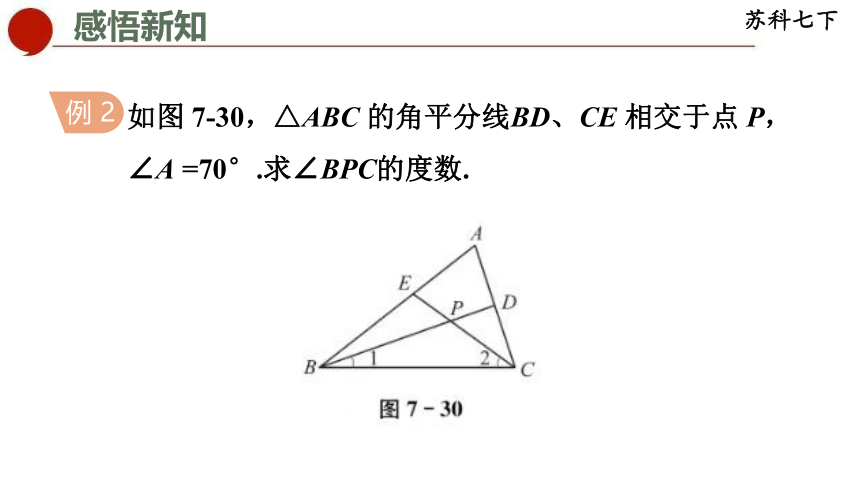
如图 7-30,△ABC 的角平分线BD、CE 相交于点 P,∠A =70°.求∠BPC的度数.
解:在ABC 中,
由∠A+∠ABC+∠ACB = 180°、 ∠A=70°,
得∠ ABC+ ∠ ACB =180°- ∠ A= 180°-70°=110°
因为 BD、CE 分别平分 ∠ ABC、 ∠ ACB,
所以∠1= ∠ABC, ∠2= ∠ACB,
∠1+∠2 = (∠ABC+∠ ACB)= ×110°= 55°.
在△PBC 中,由∠BPC+∠1+∠2=180°、 ∠ 1+∠2=55°,得∠ BPC =180°-(∠ 1+ ∠ 2)=180°-55°=125°.
解题秘方:建立三角形的模型,利用三角形的内角和求出角度解决问题.
解法提醒:
本例主要考查了建模思想,即把方位角建模成几何图形中与平行线相关的角,同时应用了平行线的性质、三角形内角和定理及直角三角形的定义等.
知识点
多边形的内角和
2
1. 多边形的定义
在平面内,由不在同一条直线上的3 条或3 条以上的线段首尾依次相接组成的图形叫做多边形.
(1) 表示方法:
表示多边形时,先写出多边形的名称,后面依次写出多边形的顶点字母.
● ● ● ●
(2)分类:
多边形按组成它的线段的条数分成三角形、四边形、五边形……三角形是最简单的多边形. 如果一个多边形由n 条线段组成,那么这个多边形就叫做n 边形.
特别解读:
多边形的三个必要条件:
1. 线段在“同一平面内”;
2. 线段“不在同一直线上”且条数不少于3;
3. 首尾依次相接.
2. 多边形的内角和公式 n 边形的内角和等于(n-2)·180°
(n ≥ 3).
验证多边形内角和公式的方法:
(1)如图7.5-3,从n 边形的一个顶点出发作对角线;
(2)如图7.5-4,在n 边形的一条边上任取一点与其他的顶点相连;
(3)如图7.5-5,在n 边形内任取一点与n 个顶点相连.
3. 思路 把多边形的内角和问题转化为三角形的内角和问题,即把多边形分成几个三角形,利用三角形的内角和推导.
[ 期中·苏州] 如果一个多边形的内角和等于720°,则它的边数为( )
A.3 B.4
C.5 D.6
D
真题2
解题秘方:紧扣多边形的内角和公式求出边数.
解:设这个正多边形的边数是n,由题意,得
(n-2)·180°= 720°,解得n = 6.
方法点拨:
已知多边形的内角和求边数n的方法:根据多边形的内角和公式列方程:(n-2)·180°=内角和,解方程求出n,即得多边形的边数.
[ 模拟· 宿迁] 如图7.5-6, 求∠ A+ ∠ ABC+ ∠ C+
∠ D+ ∠ FED+ ∠ F 的度数.
真题3
解:如图7.5-6,连接BE,因为∠ COD= ∠ BOE,
所以∠ OBE+ ∠ OEB= ∠ C+ ∠ D.
所以∠ A+ ∠ ABC+ ∠ C+ ∠ D+ ∠ FED+ ∠ F= ∠ A+ ∠ ABC+∠OBE+∠OEB+∠FED+∠F=∠A+∠ABE+∠ BEF+ ∠ F=360°.
解题秘方:由于所求的六个角不在同一个多边形中,所以考虑把它们转化到同一个多边形中. 如图7.5-6,连接BE,则这六个角的和等于四边形ABEF 的内角和.
规律点拨:
在△OCD 与△OBE 中,因为∠COD+∠C+∠D=
∠BOE+ ∠OBE+∠ OEB=180° ,且∠ COD = ∠BOE, 所以∠ OBE+ ∠ OEB=∠ C+∠D.
知识点
多边形的外角和
3
1. 多边形的外角定义
多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
2. 多边形的外角和的定义 在多边形的每个顶点处分别取多边形的一个外角,这些外角的和叫做多边形的外角和.
3. 多边形的外角和 多边形的外角和等于360° .
[ 模拟·南京] 根据下列条件解决问题:
(1)一个多边形的各内角都相等,已知其中一个外角为72°,求该多边形的边数;
解:设该多边形的边数为n.
因为多边形的各内角都相等,所以每一个外角也都相等.根据多边形的外角和为360°,
得n×72°=360°,解得n=5.
所以该多边形的边数为5.
真题4
(2)已知一个多边形的每一个外角都等于30°,求这个多边形的边数.
解:因为多边形的外角和为360°,
所以360°÷30°=12.
所以这个多边形的边数为12.
解题秘方:根据多边形的内角与外角的关系及外角和进行计算.
解法提醒:
多边形的各内角相等,从而外角也相等,已知其中一个外角的度数,由多边形的外角和是360°,即可得出边数.
n边形的内角和
等于(n-2)·180°
多边形的内角和与外角和
多边形的内角
和与外角和
三角形
多边形
三角形的内角和是180°
多边形的外
角和等于360°
第7章 平面图形的认识(二)
7.5 多边形的内角和与外角和
三角形的内角和
多边形的内角和
多边形的外角和
知识点
三角形的内角和
1
1. 三角形的内角和 三角形的内角和是180° .
表达方式:在△ ABC 中,∠ A+ ∠ B+ ∠ C=180° .
特别解读:
1. 三角形的内角和是180°揭示了三角形三个内角之间的数量关系.
2. 三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角.
2. 说明“三角形的内角和是180°”的思路
思路一: 利用“两直线平行,内错角及同位角相等”将三角形的三个内角转化为一个平角,如图7.5-1 ①所示.
思路二: 利用“两直线平行,内错角相等”将三角形的三个内角转化为两平行线间的一组同旁内角,如图7.5-1 ②所示.
例 1
在△ ABC 中,∠A=40°,∠B= ∠C,求∠C的度数;
解: 在△ ABC中,
由∠ A+ ∠ B+ ∠ C=180°,∠ A=40°,得
∠ B+ ∠ C=180°- ∠ A=180°-40°=140°,
由∠B= ∠C,得
2∠ C=140°=70°.
解题秘方:紧扣三角形的内角和是180°建立方程求解.
方法点拨:
求三角形内角的度数的方法:
1. 若已知两个角的度数,求第三个角的度数,直接利用三角形的内角和定理求解.
2. 若已知一个角的度数及另两个角之间的等量关系,或不知道任何一个角的度数,只知道三个角之间的数量关系,一般根据“三角形内角和为180°”这个隐含的等量关系列方程求解.
[ 月考· 宜兴] 若一个三角形的三个内角度数的比为
2 ∶ 3 ∶ 4,则这个三角形是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
A
真题1
解题秘方:紧扣三角形的三个内角的度数比,求出三个内角的度数,根据三个内角的度数判断三角形的形状.
另解: 设三个内角分别为2x °、3x °、4x °,
则2x+3x+4x=180. 解得x=20.所以4x = 80. 即可求解.
方法点拨:
按角判断一个三角形的形状的方法:
可以将三个角的度数分别求出;也可以看三角形中最大的角的大小:最大角是锐角,三角形就是锐角三角形;最大角是直角,三角形就是直角三角形;最大角是钝角,三角形就是钝角三角形.
例 2
如图 7-30,△ABC 的角平分线BD、CE 相交于点 P,∠A =70°.求∠BPC的度数.
解:在ABC 中,
由∠A+∠ABC+∠ACB = 180°、 ∠A=70°,
得∠ ABC+ ∠ ACB =180°- ∠ A= 180°-70°=110°
因为 BD、CE 分别平分 ∠ ABC、 ∠ ACB,
所以∠1= ∠ABC, ∠2= ∠ACB,
∠1+∠2 = (∠ABC+∠ ACB)= ×110°= 55°.
在△PBC 中,由∠BPC+∠1+∠2=180°、 ∠ 1+∠2=55°,得∠ BPC =180°-(∠ 1+ ∠ 2)=180°-55°=125°.
解题秘方:建立三角形的模型,利用三角形的内角和求出角度解决问题.
解法提醒:
本例主要考查了建模思想,即把方位角建模成几何图形中与平行线相关的角,同时应用了平行线的性质、三角形内角和定理及直角三角形的定义等.
知识点
多边形的内角和
2
1. 多边形的定义
在平面内,由不在同一条直线上的3 条或3 条以上的线段首尾依次相接组成的图形叫做多边形.
(1) 表示方法:
表示多边形时,先写出多边形的名称,后面依次写出多边形的顶点字母.
● ● ● ●
(2)分类:
多边形按组成它的线段的条数分成三角形、四边形、五边形……三角形是最简单的多边形. 如果一个多边形由n 条线段组成,那么这个多边形就叫做n 边形.
特别解读:
多边形的三个必要条件:
1. 线段在“同一平面内”;
2. 线段“不在同一直线上”且条数不少于3;
3. 首尾依次相接.
2. 多边形的内角和公式 n 边形的内角和等于(n-2)·180°
(n ≥ 3).
验证多边形内角和公式的方法:
(1)如图7.5-3,从n 边形的一个顶点出发作对角线;
(2)如图7.5-4,在n 边形的一条边上任取一点与其他的顶点相连;
(3)如图7.5-5,在n 边形内任取一点与n 个顶点相连.
3. 思路 把多边形的内角和问题转化为三角形的内角和问题,即把多边形分成几个三角形,利用三角形的内角和推导.
[ 期中·苏州] 如果一个多边形的内角和等于720°,则它的边数为( )
A.3 B.4
C.5 D.6
D
真题2
解题秘方:紧扣多边形的内角和公式求出边数.
解:设这个正多边形的边数是n,由题意,得
(n-2)·180°= 720°,解得n = 6.
方法点拨:
已知多边形的内角和求边数n的方法:根据多边形的内角和公式列方程:(n-2)·180°=内角和,解方程求出n,即得多边形的边数.
[ 模拟· 宿迁] 如图7.5-6, 求∠ A+ ∠ ABC+ ∠ C+
∠ D+ ∠ FED+ ∠ F 的度数.
真题3
解:如图7.5-6,连接BE,因为∠ COD= ∠ BOE,
所以∠ OBE+ ∠ OEB= ∠ C+ ∠ D.
所以∠ A+ ∠ ABC+ ∠ C+ ∠ D+ ∠ FED+ ∠ F= ∠ A+ ∠ ABC+∠OBE+∠OEB+∠FED+∠F=∠A+∠ABE+∠ BEF+ ∠ F=360°.
解题秘方:由于所求的六个角不在同一个多边形中,所以考虑把它们转化到同一个多边形中. 如图7.5-6,连接BE,则这六个角的和等于四边形ABEF 的内角和.
规律点拨:
在△OCD 与△OBE 中,因为∠COD+∠C+∠D=
∠BOE+ ∠OBE+∠ OEB=180° ,且∠ COD = ∠BOE, 所以∠ OBE+ ∠ OEB=∠ C+∠D.
知识点
多边形的外角和
3
1. 多边形的外角定义
多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
2. 多边形的外角和的定义 在多边形的每个顶点处分别取多边形的一个外角,这些外角的和叫做多边形的外角和.
3. 多边形的外角和 多边形的外角和等于360° .
[ 模拟·南京] 根据下列条件解决问题:
(1)一个多边形的各内角都相等,已知其中一个外角为72°,求该多边形的边数;
解:设该多边形的边数为n.
因为多边形的各内角都相等,所以每一个外角也都相等.根据多边形的外角和为360°,
得n×72°=360°,解得n=5.
所以该多边形的边数为5.
真题4
(2)已知一个多边形的每一个外角都等于30°,求这个多边形的边数.
解:因为多边形的外角和为360°,
所以360°÷30°=12.
所以这个多边形的边数为12.
解题秘方:根据多边形的内角与外角的关系及外角和进行计算.
解法提醒:
多边形的各内角相等,从而外角也相等,已知其中一个外角的度数,由多边形的外角和是360°,即可得出边数.
n边形的内角和
等于(n-2)·180°
多边形的内角和与外角和
多边形的内角
和与外角和
三角形
多边形
三角形的内角和是180°
多边形的外
角和等于360°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
