8.3 同底数幂的除法-苏科版数学七年级下册同步课件(共33张PPT)
文档属性
| 名称 | 8.3 同底数幂的除法-苏科版数学七年级下册同步课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
第8章 幂的运算
8.3 同底数幂的除法
同底数幂的除法
零指数幂
负整数指数幂
科学记数法
知识点
同底数幂的除法
1
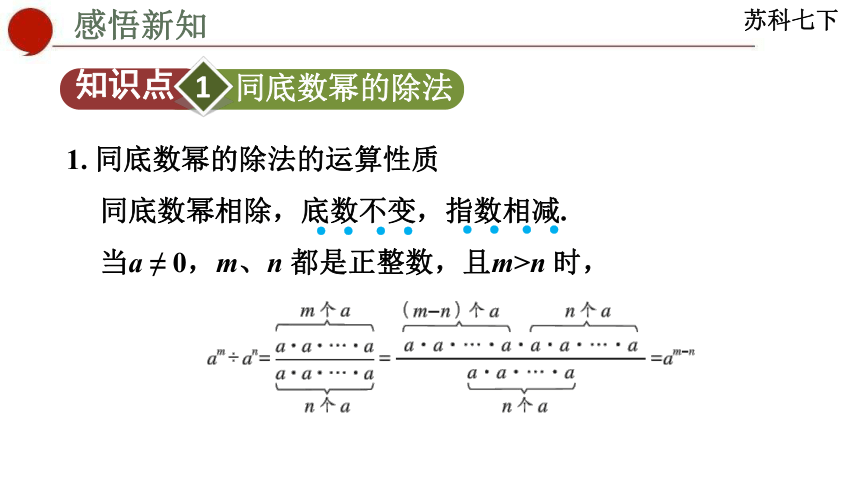
1. 同底数幂的除法的运算性质
同底数幂相除,底数不变,指数相减.
当a ≠ 0,m、n 都是正整数,且m>n 时,
● ● ● ●
● ● ● ●
于是,可得到am÷an=am-n(a ≠ 0,m、n 是正整数,m>n).
示例:
特别解读:
1. 运算性质的关键有两个:一是底数相同,二是幂相除, 二者缺一不可.
2. 底数a可以是单项式,也可以是多项式,但底数a不能为0.
3. 同底数幂相除,底数不变,指数相减,而不是相除.
2. 同底数幂的除法的运算性质的拓展运用
(1)运算性质的推广: 适用于三个及三个以上的同底数幂相除, 即am÷an÷ap=am-n-p(a ≠ 0,m、n、p 是正整数,m>n+p);
(2)同底数幂的除法的运算性质既可以正用, 也可以逆用, 逆用时am-n=am÷an(a ≠ 0,m、n 是正整数,m>n).
● ●
例 1
(1) a6÷a2 ; (2)(-b)8÷(-b) ;
(3)(ab) 4÷ (ab) 2 ; (4)t2m+3÷t2 (m是正整数).
解:(1) a6÷a2=a6-2= a3 ;
(2)(-b)8÷(-b)= (-b)8-1 = (-b)7 =-b7 ;
(3)(ab) 4÷ (ab) 2 = (ab) 4-2 = (ab) 2 = a2b2 ;
(4)t2m+3÷t2 =t2m+3-2 =t2m+1 .
方法点拨:
本题运用整体思想解题. 从整体来看各题都为同底数幂或可化为同底数幂的运算,在运算时要注意结构和符号.
1个细胞分裂1次变为2个,分裂 2 次变为4个,分裂3 次变为8个,分裂4次变为 16 个......
分裂后的细胞个数与细胞分裂的次数之间的关系,可以记为:2=2 ,4 = 2 ,8 = 2 ,16 = 24......
当这个细胞没有分裂(即分裂次数为 0)时,细胞的个数是几
想一想
你有什么猜想
想一想
观察数轴上表示 24 、 2 、 2 、2 的点的位置是如何随着指数的变化而变化的
知识点
零指数幂
2
1. 零指数幂
同底数幂相除,如果被除式的指数等于除式的指数,例如am÷am, 根据除法的意义可知所得的商为1. 另一方面,若依照同底数幂的除法来计算,则有am÷am=am-m=a0,故a0=1.
2. 零指数幂的规定
任何不等于0 的数的0 次幂等于1.
即:a0=1(a ≠ 0).
3. 拓展 零指数幂中的底数可以是一个不为0 的单项式,也可以是一个不为0的多项式.
● ● ● ●
特别解读:
1. 零指数幂在同底数幂的除法中,是除式与被除式的指数相同时的特殊情况.
2. 指数为0,但底数不能为0,因为底数为0 时,除法无意义.
例2
计算:(-2)2-12 022+(π-3.14)0.
解:原式= 4-1+1 = 4.
解题秘方:紧扣零指数幂的意义以及乘方的意义分别化简即可求解.
知识点
负整数指数幂
3
3. 特别提醒
(1)a-n 与an 互为倒数,即a-n·an=1.
(2)在幂的混合运算中,先计算乘方,再计算乘除,最后计算加减.
(3)最后结果要化成正整数指数幂的形式.
解:原式=(-1)3×23÷4+22-2+1
= -8÷4+4-2+1
= -2+4-2+1 = 1.
真题1
解题秘方:紧扣负整数指数幂的规定、零指数幂的规定等知识分别计算即可求解.
例3
解:(1) 4-2 = = ;
(2) - 3-3 = ;
(3)3.14×10-5 =3.14× = 3.14×0.00001=0.0000314 .
用小数或分数表示下列各数:
(1) 4-2 ;(2) - 3-3 ;(3)3.14×10-5 .
练习1
B
解题秘方:根据负整数指数幂与正整数指数幂互为倒数, 非零的数的零次幂等于1, 可得答案.
知识点
科学记数法
4
1. 科学记数法
(1)如果一个数的绝对值不小于10,那么可将这个数写成a×10n(1≤︱a︱<10,n 是正整数)的形式;
(2)如果一个数的绝对值较小,小于1 时,可将这个数写成a×10-n(其中n 是正整数,1 ≤ |a| < 10)的形式. 上述记数方法叫做科学记数法.
2. 用科学记数法表示小于1 的正数的一般步骤
(1)确定a:a 是大于或等于1 且小于10 的数.
(2)确定n:确定n 的方法有两个,如下:
① n 等于原数中左起第一个非0 数前0 的个数(包括小数点前的那个0);
②小数点向右移到第一个非0 的数后,小数点移动了几位,n 就等于几.
(3)将原数用科学记数法表示为a×10-n(其中1 ≤ a < 10,n 是正整数).
特别提醒:
●对于大于-1的负数也可以类似地用科学记数法表示成a×10-n的形式(其中1 ≤ |a| < 10,n是正整数),也就是说可以用科学记数法表示绝对值小于1 的数.
●用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n 前面的 “- ”号.
例 4
用科学记数法表示下列各数:
0.001 5, 0.000 109, -0.000 006 2.
解:
0.0015=1.5×0.001=1.5×10-3 ;
0.000109=1.09×0.0001=1.09×10-4;
-0.0000062=-6.2×0.000001=-6.2×10-6 .
例 5
某种细胞的截面可以近似地看成圆,它的半径约为7.80 ×10-7 m,求这种细胞的截面面积 S.
解:S=π×(7.80× 10-7 ) 2 ≈1.91× 10-12(m2).
答:该细胞的截面面积约为 1.91 × 10-12m2.
例 6
随着科学技术的发展,“纳米”常出现在人们的生活中.
纳米(记为 nm)是长度单位,它等于 1m 的十亿分之一.
以毫米为长度单位表示 1nm.
解: 1nm
解题秘方:
按照科学记数法的要求,将较小的数表示为a×10-n 的形式,其中1 ≤ |a| < 10,n 为由原数左边起第一个不为零的数字前面的0 的个数所决定.
教你一招:
用科学记数法表示绝对值小于1 的数的思路:
用科学记数法表示绝对值小于1的数时,一般形式为a×10-n,其中1 ≤ |a| < 10,n 由原数左起第一个不为0 的数字前面0 的个数所决定(包括小数点前的那个0).
同底数幂的除法
同底
数幂
的除
法
同底数幂相除
零指数幂
负整数指数幂
科学记数法
ao=1(a ≠ 0)
am÷an=am-n(a ≠ 0,m、n 是正整数,m>n)
am÷an÷ap=am-n-p(a ≠ 0,m、n、p 是正整数,m>n+p)
am-n=am÷an(a ≠ 0,m、n 是正整数,m>n)
运算
性质
推广
逆用
第8章 幂的运算
8.3 同底数幂的除法
同底数幂的除法
零指数幂
负整数指数幂
科学记数法
知识点
同底数幂的除法
1
1. 同底数幂的除法的运算性质
同底数幂相除,底数不变,指数相减.
当a ≠ 0,m、n 都是正整数,且m>n 时,
● ● ● ●
● ● ● ●
于是,可得到am÷an=am-n(a ≠ 0,m、n 是正整数,m>n).
示例:
特别解读:
1. 运算性质的关键有两个:一是底数相同,二是幂相除, 二者缺一不可.
2. 底数a可以是单项式,也可以是多项式,但底数a不能为0.
3. 同底数幂相除,底数不变,指数相减,而不是相除.
2. 同底数幂的除法的运算性质的拓展运用
(1)运算性质的推广: 适用于三个及三个以上的同底数幂相除, 即am÷an÷ap=am-n-p(a ≠ 0,m、n、p 是正整数,m>n+p);
(2)同底数幂的除法的运算性质既可以正用, 也可以逆用, 逆用时am-n=am÷an(a ≠ 0,m、n 是正整数,m>n).
● ●
例 1
(1) a6÷a2 ; (2)(-b)8÷(-b) ;
(3)(ab) 4÷ (ab) 2 ; (4)t2m+3÷t2 (m是正整数).
解:(1) a6÷a2=a6-2= a3 ;
(2)(-b)8÷(-b)= (-b)8-1 = (-b)7 =-b7 ;
(3)(ab) 4÷ (ab) 2 = (ab) 4-2 = (ab) 2 = a2b2 ;
(4)t2m+3÷t2 =t2m+3-2 =t2m+1 .
方法点拨:
本题运用整体思想解题. 从整体来看各题都为同底数幂或可化为同底数幂的运算,在运算时要注意结构和符号.
1个细胞分裂1次变为2个,分裂 2 次变为4个,分裂3 次变为8个,分裂4次变为 16 个......
分裂后的细胞个数与细胞分裂的次数之间的关系,可以记为:2=2 ,4 = 2 ,8 = 2 ,16 = 24......
当这个细胞没有分裂(即分裂次数为 0)时,细胞的个数是几
想一想
你有什么猜想
想一想
观察数轴上表示 24 、 2 、 2 、2 的点的位置是如何随着指数的变化而变化的
知识点
零指数幂
2
1. 零指数幂
同底数幂相除,如果被除式的指数等于除式的指数,例如am÷am, 根据除法的意义可知所得的商为1. 另一方面,若依照同底数幂的除法来计算,则有am÷am=am-m=a0,故a0=1.
2. 零指数幂的规定
任何不等于0 的数的0 次幂等于1.
即:a0=1(a ≠ 0).
3. 拓展 零指数幂中的底数可以是一个不为0 的单项式,也可以是一个不为0的多项式.
● ● ● ●
特别解读:
1. 零指数幂在同底数幂的除法中,是除式与被除式的指数相同时的特殊情况.
2. 指数为0,但底数不能为0,因为底数为0 时,除法无意义.
例2
计算:(-2)2-12 022+(π-3.14)0.
解:原式= 4-1+1 = 4.
解题秘方:紧扣零指数幂的意义以及乘方的意义分别化简即可求解.
知识点
负整数指数幂
3
3. 特别提醒
(1)a-n 与an 互为倒数,即a-n·an=1.
(2)在幂的混合运算中,先计算乘方,再计算乘除,最后计算加减.
(3)最后结果要化成正整数指数幂的形式.
解:原式=(-1)3×23÷4+22-2+1
= -8÷4+4-2+1
= -2+4-2+1 = 1.
真题1
解题秘方:紧扣负整数指数幂的规定、零指数幂的规定等知识分别计算即可求解.
例3
解:(1) 4-2 = = ;
(2) - 3-3 = ;
(3)3.14×10-5 =3.14× = 3.14×0.00001=0.0000314 .
用小数或分数表示下列各数:
(1) 4-2 ;(2) - 3-3 ;(3)3.14×10-5 .
练习1
B
解题秘方:根据负整数指数幂与正整数指数幂互为倒数, 非零的数的零次幂等于1, 可得答案.
知识点
科学记数法
4
1. 科学记数法
(1)如果一个数的绝对值不小于10,那么可将这个数写成a×10n(1≤︱a︱<10,n 是正整数)的形式;
(2)如果一个数的绝对值较小,小于1 时,可将这个数写成a×10-n(其中n 是正整数,1 ≤ |a| < 10)的形式. 上述记数方法叫做科学记数法.
2. 用科学记数法表示小于1 的正数的一般步骤
(1)确定a:a 是大于或等于1 且小于10 的数.
(2)确定n:确定n 的方法有两个,如下:
① n 等于原数中左起第一个非0 数前0 的个数(包括小数点前的那个0);
②小数点向右移到第一个非0 的数后,小数点移动了几位,n 就等于几.
(3)将原数用科学记数法表示为a×10-n(其中1 ≤ a < 10,n 是正整数).
特别提醒:
●对于大于-1的负数也可以类似地用科学记数法表示成a×10-n的形式(其中1 ≤ |a| < 10,n是正整数),也就是说可以用科学记数法表示绝对值小于1 的数.
●用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n 前面的 “- ”号.
例 4
用科学记数法表示下列各数:
0.001 5, 0.000 109, -0.000 006 2.
解:
0.0015=1.5×0.001=1.5×10-3 ;
0.000109=1.09×0.0001=1.09×10-4;
-0.0000062=-6.2×0.000001=-6.2×10-6 .
例 5
某种细胞的截面可以近似地看成圆,它的半径约为7.80 ×10-7 m,求这种细胞的截面面积 S.
解:S=π×(7.80× 10-7 ) 2 ≈1.91× 10-12(m2).
答:该细胞的截面面积约为 1.91 × 10-12m2.
例 6
随着科学技术的发展,“纳米”常出现在人们的生活中.
纳米(记为 nm)是长度单位,它等于 1m 的十亿分之一.
以毫米为长度单位表示 1nm.
解: 1nm
解题秘方:
按照科学记数法的要求,将较小的数表示为a×10-n 的形式,其中1 ≤ |a| < 10,n 为由原数左边起第一个不为零的数字前面的0 的个数所决定.
教你一招:
用科学记数法表示绝对值小于1 的数的思路:
用科学记数法表示绝对值小于1的数时,一般形式为a×10-n,其中1 ≤ |a| < 10,n 由原数左起第一个不为0 的数字前面0 的个数所决定(包括小数点前的那个0).
同底数幂的除法
同底
数幂
的除
法
同底数幂相除
零指数幂
负整数指数幂
科学记数法
ao=1(a ≠ 0)
am÷an=am-n(a ≠ 0,m、n 是正整数,m>n)
am÷an÷ap=am-n-p(a ≠ 0,m、n、p 是正整数,m>n+p)
am-n=am÷an(a ≠ 0,m、n 是正整数,m>n)
运算
性质
推广
逆用
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
