【备考2023】浙教版科学“冲刺重高”压轴训练(八):力学【word,含答案】
文档属性
| 名称 | 【备考2023】浙教版科学“冲刺重高”压轴训练(八):力学【word,含答案】 |  | |
| 格式 | doc | ||
| 文件大小 | 498.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-05-12 21:51:06 | ||
图片预览



文档简介
【运动和力】
1.观察如图所示的小旗,关于甲、乙两船相对于楼房的运动情况,下列说法正确的是( )
A.甲船向右运动,乙船一定静止
B.甲船向左运动,乙船一定运动
C.甲船向右运动,乙船可能静止
D.甲船向左运动,乙船可能运动
2.在汽车中悬线上挂一个小球,当汽车运动时,悬线将与竖直方向成某一固定角度,如图所示,若在汽车底板上还有一个跟其相对静止的物体M,则关于汽车的运动情况和物体M的受力情况正确的是( )
A.汽车一定向右做加速运动
B.汽车一定向左做加速运动
C.M除受到重力、底板的支持力作用外,还一定受到向右的摩擦力作用
D.M除受到重力、底板的支持力作用外,还可能受到向左的摩擦力作用
3.有两根完全相同的轻质弹簧,原长10cm。若一根弹簧两端受到10N的压力时,弹簧长度压缩到5cm。如图所示,第一次将一根弹簧水平压在墙壁和甲物体之间,使弹簧长度为5cm,弹簧和甲物体处于静止状态。第二次再将另一根弹簧放在甲和乙物体之间,使两根弹簧都被压缩到5cm且处于同一水平直线上,甲、乙两物体都处于静止状态。若甲和乙是两个完全相同的正方体,重力都是50N。下列说法错误的是( )
A.第一次时,甲受到水平向左的摩擦力
B.第二次时,甲没有受到地面的摩擦力
C.两次实验中,墙壁均受到10N的推力
D.乙受到地面20N的摩擦力,方向为水平向左
4.如图所示,质量为m的物体放在竖直放置的钢板轨道AB之间,钢板固定不动,物体刚好以速度v向下匀速运动,若要使物体以速度3v沿钢板向上匀速运动,则需要施加的拉力F的大小应该等于( )
A.mg B.2mg C.3mg D.6mg
5.甲、乙两辆汽车沿平直的公路从同一地点同时驶向同一目的地,甲车在前一半时间以速度v1做匀速运动,在后一半时间以速度v2做匀速运动(v1≠v2);乙车在前一半路程以速度v1做匀速运动,在后一半路程以速度v2做匀速运动,则( )
A.甲车先到达
B.乙车先到达
C.同时到达
D.因不知道v1、v2大小关系,因此无法确定谁先到达
6.初中科学中把物体在单位时间内通过的路程叫速度,速度计算公式为:速度=路程/时间,即v=s/t。高中物理中把物体在单位时间内速度的变化量叫加速度(注:速度的变化量用△v表示,它等于前后速度之差;加速度用字母a表示,国际单位是m/s2)。由加速度的定义可知:
(1)若一个物体开始运动的速度v0=2m/s,经过5s后它的速度变为v1=6m/s,若物体做匀加速直线运动(单位时间内速度的增加量相等),求出物体的加速度大小a=
m/s2;
(2)匀速直线运动的v﹣t图如图(甲)所示,图中阴影部分面积表示以速度v匀速直线运动的物体,运动时间为t时通过的路程s;匀加速直线运动的v﹣t图如图(乙)所示,其中阴影部分面积表示做匀加速直线运动物体,速度由v0到v1,运动时间为t时通过的路程s;用v0、t、a写出S的表达式,s= 。
【密度、压强和浮力】
1.如图所示,两个完全相同的量筒分别盛有质量相等的水和煤油(ρ水>ρ油),A,B两点到液面的距离相等,A,C两点到容器底面的距离相等,则有( )
A.两个容器底面受到的液体压强不相等
B.A,B两点的液体压强相等
C.A点的液体压强大于C点的液体压强
D.A点的液体压强小于C点的液体压强
2.水平桌面上放有甲、乙两个完全相同的柱状容器。在甲容器内倒入部分液体A,在乙容器内倒入部分液体A和水(液体和水不相溶,且ρA>ρ水)。然后分别在两容器内放入质量相等的冰块,此时甲容器内液面和乙容器内液面恰好相平,如图所示。若冰块全部熔化后,甲、乙两容器内水面距离容器底部分别为h1和h2,水和液体A之间的界面距离容器底部分别为h1′和h2′,则( )
A.h1>h2,h1′>h2′ B.h1<h2,h1′>h2′
C.h1>h2,h1′<h2′ D.h1<h2,h1′<h2′
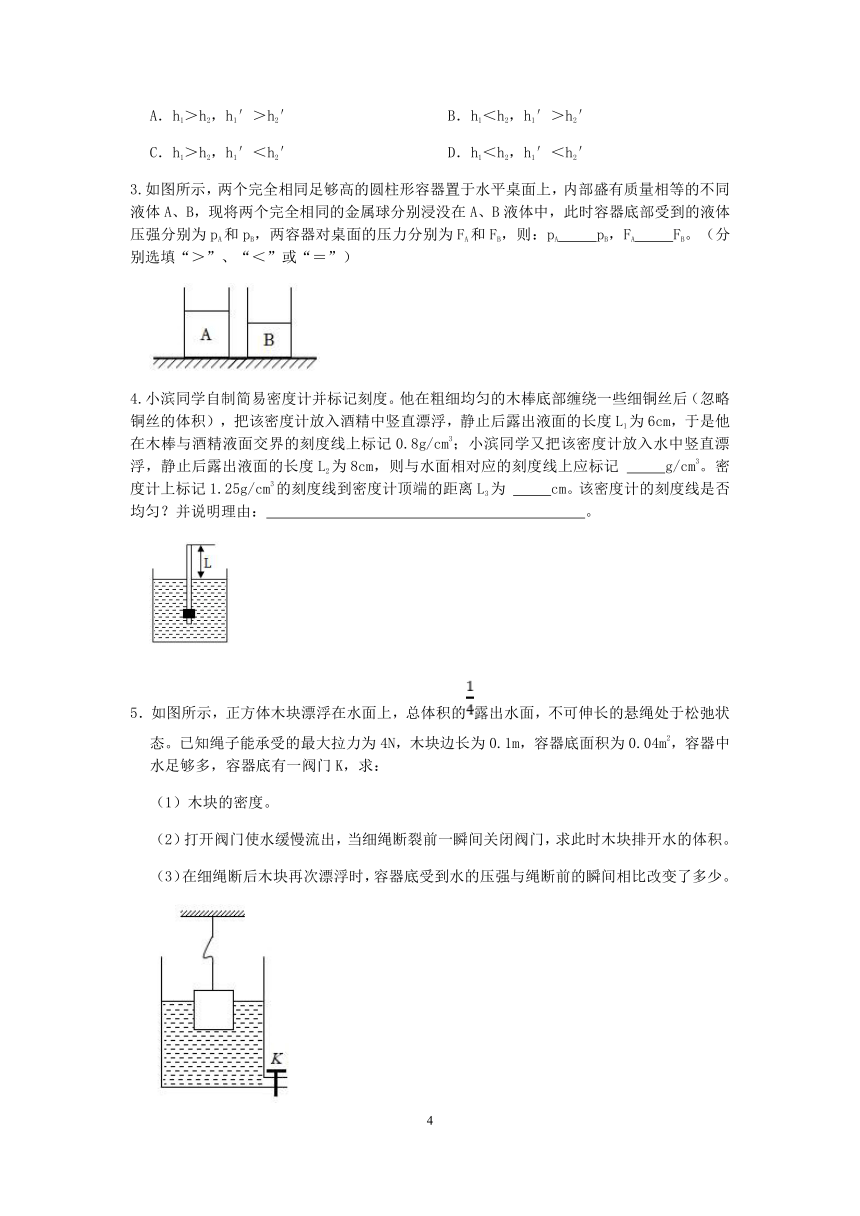
3.如图所示,两个完全相同足够高的圆柱形容器置于水平桌面上,内部盛有质量相等的不同液体A、B,现将两个完全相同的金属球分别浸没在A、B液体中,此时容器底部受到的液体压强分别为pA和pB,两容器对桌面的压力分别为FA和FB,则:pA pB,FA FB。(分别选填“>”、“<”或“=”)
4.小滨同学自制简易密度计并标记刻度。他在粗细均匀的木棒底部缠绕一些细铜丝后(忽略铜丝的体积),把该密度计放入酒精中竖直漂浮,静止后露出液面的长度L1为6cm,于是他在木棒与酒精液面交界的刻度线上标记0.8g/cm3;小滨同学又把该密度计放入水中竖直漂浮,静止后露出液面的长度L2为8cm,则与水面相对应的刻度线上应标记 g/cm3。密度计上标记1.25g/cm3的刻度线到密度计顶端的距离L3为 cm。该密度计的刻度线是否均匀?并说明理由: 。
5.如图所示,正方体木块漂浮在水面上,总体积的露出水面,不可伸长的悬绳处于松弛状态。已知绳子能承受的最大拉力为4N,木块边长为0.1m,容器底面积为0.04m2,容器中水足够多,容器底有一阀门K,求:
(1)木块的密度。
(2)打开阀门使水缓慢流出,当细绳断裂前一瞬间关闭阀门,求此时木块排开水的体积。
(3)在细绳断后木块再次漂浮时,容器底受到水的压强与绳断前的瞬间相比改变了多少。
【杠杆的动态平衡】
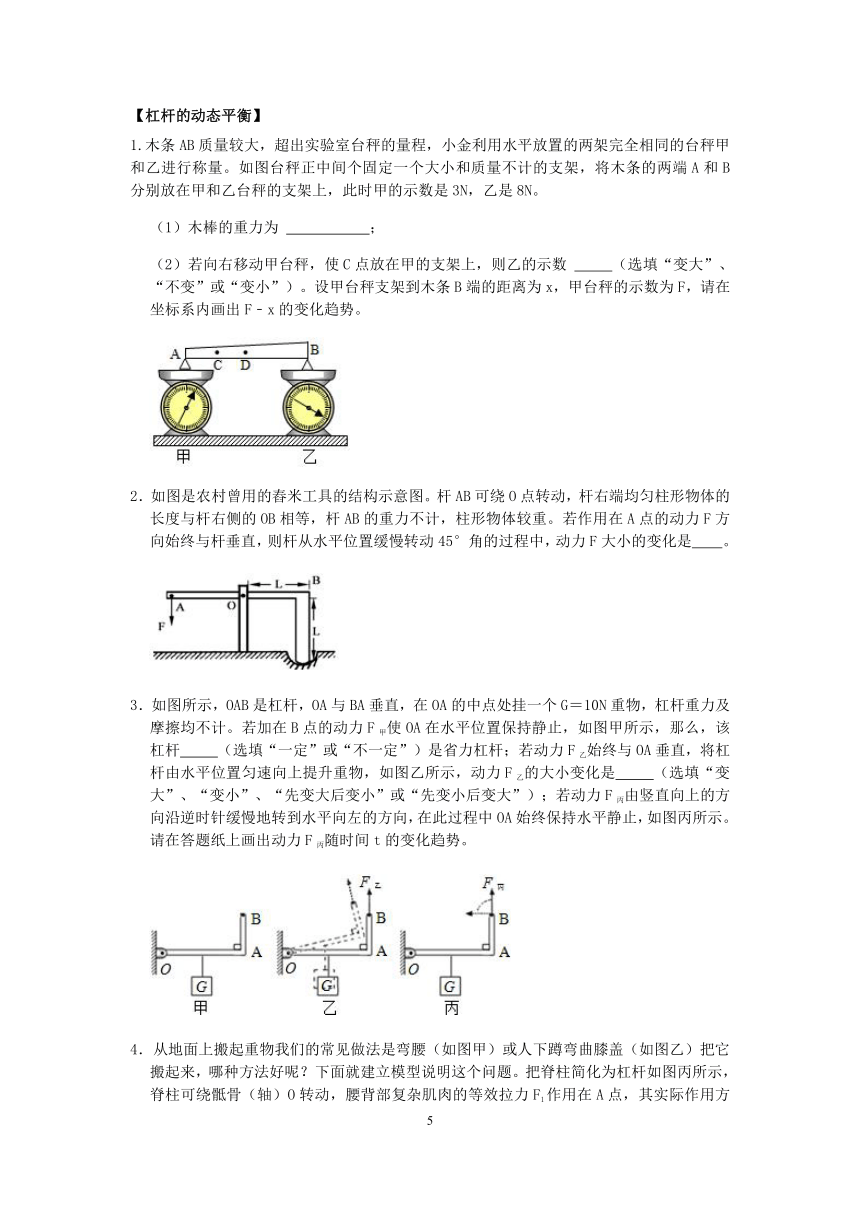
1.木条AB质量较大,超出实验室台秤的量程,小金利用水平放置的两架完全相同的台秤甲和乙进行称量。如图台秤正中间个固定一个大小和质量不计的支架,将木条的两端A和B分别放在甲和乙台秤的支架上,此时甲的示数是3N,乙是8N。
(1)木棒的重力为 ;
(2)若向右移动甲台秤,使C点放在甲的支架上,则乙的示数 (选填“变大”、“不变”或“变小”)。设甲台秤支架到木条B端的距离为x,甲台秤的示数为F,请在坐标系内画出F﹣x的变化趋势。
2.如图是农村曾用的舂米工具的结构示意图。杆AB可绕O点转动,杆右端均匀柱形物体的长度与杆右侧的OB相等,杆AB的重力不计,柱形物体较重。若作用在A点的动力F方向始终与杆垂直,则杆从水平位置缓慢转动45°角的过程中,动力F大小的变化是 。
3.如图所示,OAB是杠杆,OA与BA垂直,在OA的中点处挂一个G=10N重物,杠杆重力及摩擦均不计。若加在B点的动力F甲使OA在水平位置保持静止,如图甲所示,那么,该杠杆 (选填“一定”或“不一定”)是省力杠杆;若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,如图乙所示,动力F乙的大小变化是 (选填“变大”、“变小”、“先变大后变小”或“先变小后变大”);若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向,在此过程中OA始终保持水平静止,如图丙所示。请在答题纸上画出动力F丙随时间t的变化趋势。
4.从地面上搬起重物我们的常见做法是弯腰(如图甲)或人下蹲弯曲膝盖(如图乙)把它搬起来,哪种方法好呢?下面就建立模型说明这个问题。把脊柱简化为杠杆如图丙所示,脊柱可绕骶骨(轴)O转动,腰背部复杂肌肉的等效拉力F1作用在A点,其实际作用方向与脊柱夹角为12°且保持不变,搬箱子拉力F2作用在肩关节B点,在B点挂一重物代替箱子。用测力计沿F1方向拉,使模型静止,可测出腰背部复杂肌肉拉力的大小。接着,改变脊柱与水平面的夹角即可改变杠杆与水平面的夹角α,多次实验得出结论。
(1)在丙图中画出F2力臂L2。
(2)当α角增大时,L2 (变大/不变/变小),F1 (变大/不变/变小)。
(3)如果考虑到人上半身的重力,那么腰背部肌肉的实际拉力将比丙图中F1要 (大/小)。
(4)对比甲、乙两种姿势所对应丙图中的两种状态,由以下分析可得, (甲/乙)图中的姿势比较正确。
参考答案
【运动和力】
1.解:由图中的信息可以判断出:因为房子的烟向右飘,所以风是向右吹
所以乙车运动状态有三种可能 1、向左运动;2、静止;3、向右运动,但速度小于风速;
因为甲车旗向左飘,所以甲车只能向右运动,且速度要大于风的速度。
故选:C。
2.解:
AB、以小球为研究对象,小球向左运动,所以有两种可能,即可能向右做加速运动,也可能向左做减速运动,故AB错误;
CD、据上面的分析可知,木块M相对于汽车有一个向左的运动趋势,此时木块M会受到一个向右的摩擦力(其动力的作用),故M除受到重力、底板的支持力作用外,还一定受到向右的摩擦力作用,故C正确,D错误;
故选:C。
3.解:A.第一次弹簧被压缩至5cm,所以弹簧对墙壁和甲的弹力均为10N,甲处于静止状态且受到水平向右的弹力,由二力平衡可知甲受到10N的水平向左的摩擦力,故A正确;
B.第二次两个弹簧均被压缩到5cm,所以甲受到水平向左和水平向右的弹力均为10N,这两个力是一对平衡力,所以甲不会受到摩擦力,故B正确;
C.两次实验中,弹簧均被压缩至5cm,所以弹簧的弹力均为10N,即墙壁受到的推力均为10N,故C正确;
D.乙受到弹簧水平向右10N的弹力,此时乙处于静止状态,由二力平衡可知此时乙还受到水平向左的10N的摩擦力,故D错误。
故选:D。
4.解:物体以速度v向下匀速运动时,受到竖直向下的重力G=mg、竖直向上的摩擦力f,
物体处于平衡状态,由平衡条件得:f=mg;
物体以速度3v沿钢板向上匀速运动时,物体受到竖直向下的重力mg,竖直向下的摩擦力f,竖直向上的拉力F,
由于物体与钢板间的接触面、物体间的压力不变,物体与钢板间的摩擦力不变,即f=mg,
由平衡条件得:F=mg+f=2mg;
故选:B。
5.解:设两地之间的距离为s,甲运动的时间为t1,乙运动的时间为t2,
由v得,
甲前一半时间通过的路程为t1v1,后一半时间通过的路程为t1v2,则有:st1v1t1v2,t1;
乙前一半路程所用时间为,后一半路程所用时间为,
则有:t2,
则t2﹣t10;
故t2>t1,即甲车用的时间少,即甲车先到达,故A正确,B、C、D错误。
故选:A。
6.解:(1)物体在5s内的速度变化量△v=v1﹣v0=6m/s﹣2m/s=4m/s;
则物体的加速度大小:a0.8m/s2;
(2)由加速度的定义可知:a,
由题意可知,图乙中阴影部分的面积表示做匀加速直线运动的物体速度由v0到v1,运动时间为t通过的路程,且图乙中阴影部分的面积等于长方形的面积和三角形的面积之和,
则物体通过的路程:s=S长方形+S三角形=v0t(v1﹣v0)t=v0tt2=v0tat2。
故答案为:(1)0.8;(2)v0tat2。
【密度、压强和浮力】
1.解:A、两个完全相同的量筒分别盛有质量相等的水和煤油,所以两个容器底面受到的液体压力相等且等于液体的重力,所以压强相等,故A不符合题意;
B、A、B两点到液面的距离相等即同深度,利用压强计算公式p=ρgh可知,由于水的密度大于煤油的密度,所以,A点的压强大于B点的压强,故B不符合题意;
CD、A、C两点到容器底面的距离相等,煤油的密度小于水的密度,根据公式p=ρgh可知,A、C点以下部分的液体产生的压强是水中的压强大,煤油中的压强小。又因为两只量筒中液体对底面的压强相等,总压强减去A、C点以下部分的压强就等于A、C点以上部分产生的压强,因此可得出,A点的压强小于C点的压强。故C不符合题意,D符合题意。
故选:D。
2.解:(1)图甲中:由于冰块都处于漂浮状态,则:F甲浮=G冰,
根据阿基米德原理可得:F甲浮=ρAgV排甲,
所以,ρAgV排甲=G冰;
则:V排甲;
当冰全部熔化后由于冰的质量不变,即:G水=G冰,
则冰熔化后的水的体积为:V水;
由于ρA>ρ水,则:V排甲<V水,
所以,△V甲=V水﹣V排甲G冰;
图乙中:设冰块漂浮在水和液体A的冰块分为G1、G2;且G1+G2=G冰;
则由于冰块都处于漂浮状态,F水浮=G1;FA浮=G2;
根据阿基米德原理可得:F水浮=ρ水gV排水;FA浮=ρAgV排A;
则:ρ水gV排水=G1;ρAgV排A=G2;
所以,V排水,V排A;
则:V排乙=V排水+V排A;
当冰全部熔化后由于冰的质量不变,即:G水1=G1;G水2=G2;
则冰熔化后的水的体积为:V水乙=V水1+V水2
由于ρA>ρ水,则:V排乙<V水乙,
所以,△V乙=V水乙﹣V排乙()G2;
由于G1+G2=G冰;所以,△V甲>△V乙,
已知甲、乙两个完全相同的柱状容器。所以,根据h可知:
容器中液面升高的高度△h甲>△h乙;
由于冰块没有熔化前甲容器内液面和乙容器内液面恰好相平,所以,若冰块全部熔化后,甲容器内液面距离容器底部的高度h1大于乙容器内液面距离容器底部的高度h2;故BD错误;
(2)由于液体和水不相溶且ρA>ρ水,则冰熔化后,液体A会在容器的底部,由图可知:容器里液体A的体积关系是:V甲A>V乙A,由于甲乙容器完全相同,则根据h可知:
液体A的深度关系是:h1′>h2′,故A正确,C错误。
故选:A。
3.解:由图可知,A液体的体积要大于B液体的体积,液体A、B的质量相同,根据ρ可知,ρA<ρB;
容器为圆柱形容器,液体对容器底的压力F=G=mg,由于A液体的质量等于B液体的质量,所以A液体对容器底的压力等于B液体对容器底的压力;而两个圆柱形容器完全相同、底面积相同,所以由p可知A容器底受到的液体压强等于B容器底受到的液体压强;
将两个完全相同的金属球分别投入两容器中都浸没,且两容器均没有液体溢出,所以排开液体的体积相同,即液面升高的高度相同;
根据液体压强的公式p=ρgh可知,ΔpA=ρAgΔh,ΔpB=ρBgΔh,由于ρA<ρB,则ΔpA<ΔpB,所以将两个完全相同的金属球分别投入两容器中时,容器底部受到的压强关系为:pA<pB;
根据题意可知,容器质量相同、液体质量相同、小球质量相同,则两个容器的总质量相同,由G=mg可知,两容器的总重力相同,都在水平面上,容器对水平面的压力等于其重力,故压力相同,即,FA=FB。
故答案为:<;=。
4.解:设木棒长度为h,底面积为S,密度计重力为G,小滨将该密度计放入酒精中,密度计静止时L1为6cm,ρ酒精=0.8g/cm3=0.8×103kg/m3,
由F浮酒精=G,可得:ρ酒精gV排酒精=G,
即[(h﹣0.06m)S]×0.8×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣①,
小滨将该密度计放入水中,密度计静止时L2为8cm,由于水的密度ρ水=1.0g/cm3=1.0×103kg/m3,则与水面相对应的刻度线上应标记1.0g/cm3。
由F浮水=G,可得:
[(h﹣0.08m)S]×1.0×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣②,
由①②可得,h=0.16m;
设该密度计上对应密度值为1.25g/cm3的刻度线到密度计顶端的距离为L′,
则[(h﹣L′)S]×1.25×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣③,
将h=0.16m分别代入②和③,并将②③联立,
解得L=0.096m=9.6cm;
当密度计漂浮在密度为ρ液的液体中时,
因密度计始终漂浮,受到的浮力和自身的重力相等,
所以,G=F浮液,即ρgSh=ρ液gSh液,
整理可得:h液h,
由表达式可知,h液和ρ液是反比例函数,所以这种密度计的刻度是不均匀。
故答案为:1.0;9.6;不均匀,由表达式h液h可知,h液和ρ液是反比例函数。
5.解:
(1)木块漂浮,根据浮沉条件可知,F浮=G木,
根据阿基米德原理可知:F浮=ρ水V排g,木块的重力为:G木=ρ木V木g,
则:ρ水V排g=ρ木V木g,
木块总体积的露出水面,所以V排V木,
木块的密度为:ρ木ρ水1×103kg/m3=0.75×103kg/m3;
(2)如图:
当细绳断裂时,F浮′+F最大=G木,
设此时木块排开水的体积为V排′,则:
ρ水V排′g+F最大=ρ木V木g,
即:1×103kg/m3×V排′×10N/kg+4N=0.75×103kg/m3×(0.1m)3×10N/kg,
解得:
V排′=3.5×10﹣4m3;
(3)在细绳断开后木块再次漂浮时,浮力增加4N,排开水体积增加:
△V排4×10﹣4m3,
水面上升:
△h0.01m,
△p=ρg△h=1×103kg/m3×10N/kg×0.01m=100Pa。
即:容器底受水的压强增大了100Pa。
答:(1)木块的密度为0.75×103kg/m3;
(2)当细绳断裂前一瞬间关闭阀门,此时木块排开水的体积为3.5×10﹣4m3;
(3)在细绳断开后木块再次漂浮时,容器底受到水的压强与断绳前的瞬间相比,容器底受水的压强增大了100Pa。
【杠杆的动态平衡】
1.解:
(1)木条受到竖直向下的重力和支架对木条竖直向上的支持力,由二力平衡,G=FA+FB,
两支架对木条的支持力和木条对托盘的压力为作用力和反作用力,大小相等,故木棒的重力为:
G=3N+8N=11N;
(2)O为木条的重心,若向右移动甲台秤,使C点放在甲的支架上,以B为支点,木条的重力G为阻力,C点对木条的支持力FC为动力,杠杆的示意图如图1所示:
由杠杆的平衡条件,G×LB=FC×(LC+LB),
因G和LB不变,当向右移动甲台秤,使C点放在甲的支架上,LC变小,故动力臂变小,故FC变大,因乙台秤示数等于木条的重力与甲台秤示数,故则乙的示数变小;
设甲台秤支架到木条B端的距离为x,甲台秤的示数为F,
由杠杆的平衡条件,G×LB=F×x,
故F,因G与LB都不变,为一常数,故F与x为反比例函数,如下图2所示:
故答案为:(1)11N;(2)变小;如图2所示。
2.解:动力F的方向始终与杆垂直,故动力臂不变;
阻力是柱形物体的重,阻力作用点在柱形物体的重心上;
如下图所示(只画了杠杆的右侧部分,图中虚线为重心运动的路线):
0位置为原来的位置,1位置为阻力臂最大的位置,2位置为转过45°的位置,
由上图可知,整个过程中阻力臂先变大后变小;
因动力臂不变,阻力G不变,阻力臂先变大后变小,由杠杆平衡条件可知,动力F先增大后减小。
故答案为:先增大后减小。
3.解:
(1)由题只知道动力的作用点在B点,不知道动力的作用方向,所以也就不知道动力臂的大小,所以也就无法比较动力臂和阻力臂的大小关系,所以无法确定它是哪种杠杆;
(2)若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,此过程中,阻力和动力臂不变,阻力臂逐渐减小,根据杠杆的平衡条件可知动力变小;
(3)如图所示,
由图可知,当F丙由竖直向上的位置沿逆时针方向缓慢的转到水平向左的位置时,动力臂先变大后变小,阻力与阻力臂不变,由杠杆平衡条件可知,动力先变小后变大。且上图可以看出,F丙水平时,比F垂直OA时力臂小,所以动力更大。
动力F丙随时间t的变化趋势如图所示:
故答案为:不一定;变小;见上图。
4.解:(1)延长F2作用线,由支点作其作用线的垂线,L2是其力臂。如图:
(2)由图可知:当α角增大时,力臂L2变小;由于拉力F1的方向与脊柱夹角始终为12°,且OA这段距离不变,则O点到F1作用线的距离不变,即动力臂不变,阻力为箱子的重力不变,根据杠杆平衡条件可知,F1变小;
(3)如果考虑到人上半身的重力,由于上半身的重力会阻碍杠杆的转动,根据杠杆平衡条件可知:实际拉力将变大;
(4)比较甲、乙两种姿势可知:甲的支点太高,在搬起物体时,阻力臂减小得慢,则腰背部复杂肌肉的等效拉力F1要比较长时间的使用较大的力,所以甲姿势不正确,乙姿势比较正确。
故答案为:(1)如上图;(2)变小;变小;(3)大;(4)乙
力学
1.观察如图所示的小旗,关于甲、乙两船相对于楼房的运动情况,下列说法正确的是( )
A.甲船向右运动,乙船一定静止
B.甲船向左运动,乙船一定运动
C.甲船向右运动,乙船可能静止
D.甲船向左运动,乙船可能运动
2.在汽车中悬线上挂一个小球,当汽车运动时,悬线将与竖直方向成某一固定角度,如图所示,若在汽车底板上还有一个跟其相对静止的物体M,则关于汽车的运动情况和物体M的受力情况正确的是( )
A.汽车一定向右做加速运动
B.汽车一定向左做加速运动
C.M除受到重力、底板的支持力作用外,还一定受到向右的摩擦力作用
D.M除受到重力、底板的支持力作用外,还可能受到向左的摩擦力作用
3.有两根完全相同的轻质弹簧,原长10cm。若一根弹簧两端受到10N的压力时,弹簧长度压缩到5cm。如图所示,第一次将一根弹簧水平压在墙壁和甲物体之间,使弹簧长度为5cm,弹簧和甲物体处于静止状态。第二次再将另一根弹簧放在甲和乙物体之间,使两根弹簧都被压缩到5cm且处于同一水平直线上,甲、乙两物体都处于静止状态。若甲和乙是两个完全相同的正方体,重力都是50N。下列说法错误的是( )
A.第一次时,甲受到水平向左的摩擦力
B.第二次时,甲没有受到地面的摩擦力
C.两次实验中,墙壁均受到10N的推力
D.乙受到地面20N的摩擦力,方向为水平向左
4.如图所示,质量为m的物体放在竖直放置的钢板轨道AB之间,钢板固定不动,物体刚好以速度v向下匀速运动,若要使物体以速度3v沿钢板向上匀速运动,则需要施加的拉力F的大小应该等于( )
A.mg B.2mg C.3mg D.6mg
5.甲、乙两辆汽车沿平直的公路从同一地点同时驶向同一目的地,甲车在前一半时间以速度v1做匀速运动,在后一半时间以速度v2做匀速运动(v1≠v2);乙车在前一半路程以速度v1做匀速运动,在后一半路程以速度v2做匀速运动,则( )
A.甲车先到达
B.乙车先到达
C.同时到达
D.因不知道v1、v2大小关系,因此无法确定谁先到达
6.初中科学中把物体在单位时间内通过的路程叫速度,速度计算公式为:速度=路程/时间,即v=s/t。高中物理中把物体在单位时间内速度的变化量叫加速度(注:速度的变化量用△v表示,它等于前后速度之差;加速度用字母a表示,国际单位是m/s2)。由加速度的定义可知:
(1)若一个物体开始运动的速度v0=2m/s,经过5s后它的速度变为v1=6m/s,若物体做匀加速直线运动(单位时间内速度的增加量相等),求出物体的加速度大小a=
m/s2;
(2)匀速直线运动的v﹣t图如图(甲)所示,图中阴影部分面积表示以速度v匀速直线运动的物体,运动时间为t时通过的路程s;匀加速直线运动的v﹣t图如图(乙)所示,其中阴影部分面积表示做匀加速直线运动物体,速度由v0到v1,运动时间为t时通过的路程s;用v0、t、a写出S的表达式,s= 。
【密度、压强和浮力】
1.如图所示,两个完全相同的量筒分别盛有质量相等的水和煤油(ρ水>ρ油),A,B两点到液面的距离相等,A,C两点到容器底面的距离相等,则有( )
A.两个容器底面受到的液体压强不相等
B.A,B两点的液体压强相等
C.A点的液体压强大于C点的液体压强
D.A点的液体压强小于C点的液体压强
2.水平桌面上放有甲、乙两个完全相同的柱状容器。在甲容器内倒入部分液体A,在乙容器内倒入部分液体A和水(液体和水不相溶,且ρA>ρ水)。然后分别在两容器内放入质量相等的冰块,此时甲容器内液面和乙容器内液面恰好相平,如图所示。若冰块全部熔化后,甲、乙两容器内水面距离容器底部分别为h1和h2,水和液体A之间的界面距离容器底部分别为h1′和h2′,则( )
A.h1>h2,h1′>h2′ B.h1<h2,h1′>h2′
C.h1>h2,h1′<h2′ D.h1<h2,h1′<h2′
3.如图所示,两个完全相同足够高的圆柱形容器置于水平桌面上,内部盛有质量相等的不同液体A、B,现将两个完全相同的金属球分别浸没在A、B液体中,此时容器底部受到的液体压强分别为pA和pB,两容器对桌面的压力分别为FA和FB,则:pA pB,FA FB。(分别选填“>”、“<”或“=”)
4.小滨同学自制简易密度计并标记刻度。他在粗细均匀的木棒底部缠绕一些细铜丝后(忽略铜丝的体积),把该密度计放入酒精中竖直漂浮,静止后露出液面的长度L1为6cm,于是他在木棒与酒精液面交界的刻度线上标记0.8g/cm3;小滨同学又把该密度计放入水中竖直漂浮,静止后露出液面的长度L2为8cm,则与水面相对应的刻度线上应标记 g/cm3。密度计上标记1.25g/cm3的刻度线到密度计顶端的距离L3为 cm。该密度计的刻度线是否均匀?并说明理由: 。
5.如图所示,正方体木块漂浮在水面上,总体积的露出水面,不可伸长的悬绳处于松弛状态。已知绳子能承受的最大拉力为4N,木块边长为0.1m,容器底面积为0.04m2,容器中水足够多,容器底有一阀门K,求:
(1)木块的密度。
(2)打开阀门使水缓慢流出,当细绳断裂前一瞬间关闭阀门,求此时木块排开水的体积。
(3)在细绳断后木块再次漂浮时,容器底受到水的压强与绳断前的瞬间相比改变了多少。
【杠杆的动态平衡】
1.木条AB质量较大,超出实验室台秤的量程,小金利用水平放置的两架完全相同的台秤甲和乙进行称量。如图台秤正中间个固定一个大小和质量不计的支架,将木条的两端A和B分别放在甲和乙台秤的支架上,此时甲的示数是3N,乙是8N。
(1)木棒的重力为 ;
(2)若向右移动甲台秤,使C点放在甲的支架上,则乙的示数 (选填“变大”、“不变”或“变小”)。设甲台秤支架到木条B端的距离为x,甲台秤的示数为F,请在坐标系内画出F﹣x的变化趋势。
2.如图是农村曾用的舂米工具的结构示意图。杆AB可绕O点转动,杆右端均匀柱形物体的长度与杆右侧的OB相等,杆AB的重力不计,柱形物体较重。若作用在A点的动力F方向始终与杆垂直,则杆从水平位置缓慢转动45°角的过程中,动力F大小的变化是 。
3.如图所示,OAB是杠杆,OA与BA垂直,在OA的中点处挂一个G=10N重物,杠杆重力及摩擦均不计。若加在B点的动力F甲使OA在水平位置保持静止,如图甲所示,那么,该杠杆 (选填“一定”或“不一定”)是省力杠杆;若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,如图乙所示,动力F乙的大小变化是 (选填“变大”、“变小”、“先变大后变小”或“先变小后变大”);若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向,在此过程中OA始终保持水平静止,如图丙所示。请在答题纸上画出动力F丙随时间t的变化趋势。
4.从地面上搬起重物我们的常见做法是弯腰(如图甲)或人下蹲弯曲膝盖(如图乙)把它搬起来,哪种方法好呢?下面就建立模型说明这个问题。把脊柱简化为杠杆如图丙所示,脊柱可绕骶骨(轴)O转动,腰背部复杂肌肉的等效拉力F1作用在A点,其实际作用方向与脊柱夹角为12°且保持不变,搬箱子拉力F2作用在肩关节B点,在B点挂一重物代替箱子。用测力计沿F1方向拉,使模型静止,可测出腰背部复杂肌肉拉力的大小。接着,改变脊柱与水平面的夹角即可改变杠杆与水平面的夹角α,多次实验得出结论。
(1)在丙图中画出F2力臂L2。
(2)当α角增大时,L2 (变大/不变/变小),F1 (变大/不变/变小)。
(3)如果考虑到人上半身的重力,那么腰背部肌肉的实际拉力将比丙图中F1要 (大/小)。
(4)对比甲、乙两种姿势所对应丙图中的两种状态,由以下分析可得, (甲/乙)图中的姿势比较正确。
参考答案
【运动和力】
1.解:由图中的信息可以判断出:因为房子的烟向右飘,所以风是向右吹
所以乙车运动状态有三种可能 1、向左运动;2、静止;3、向右运动,但速度小于风速;
因为甲车旗向左飘,所以甲车只能向右运动,且速度要大于风的速度。
故选:C。
2.解:
AB、以小球为研究对象,小球向左运动,所以有两种可能,即可能向右做加速运动,也可能向左做减速运动,故AB错误;
CD、据上面的分析可知,木块M相对于汽车有一个向左的运动趋势,此时木块M会受到一个向右的摩擦力(其动力的作用),故M除受到重力、底板的支持力作用外,还一定受到向右的摩擦力作用,故C正确,D错误;
故选:C。
3.解:A.第一次弹簧被压缩至5cm,所以弹簧对墙壁和甲的弹力均为10N,甲处于静止状态且受到水平向右的弹力,由二力平衡可知甲受到10N的水平向左的摩擦力,故A正确;
B.第二次两个弹簧均被压缩到5cm,所以甲受到水平向左和水平向右的弹力均为10N,这两个力是一对平衡力,所以甲不会受到摩擦力,故B正确;
C.两次实验中,弹簧均被压缩至5cm,所以弹簧的弹力均为10N,即墙壁受到的推力均为10N,故C正确;
D.乙受到弹簧水平向右10N的弹力,此时乙处于静止状态,由二力平衡可知此时乙还受到水平向左的10N的摩擦力,故D错误。
故选:D。
4.解:物体以速度v向下匀速运动时,受到竖直向下的重力G=mg、竖直向上的摩擦力f,
物体处于平衡状态,由平衡条件得:f=mg;
物体以速度3v沿钢板向上匀速运动时,物体受到竖直向下的重力mg,竖直向下的摩擦力f,竖直向上的拉力F,
由于物体与钢板间的接触面、物体间的压力不变,物体与钢板间的摩擦力不变,即f=mg,
由平衡条件得:F=mg+f=2mg;
故选:B。
5.解:设两地之间的距离为s,甲运动的时间为t1,乙运动的时间为t2,
由v得,
甲前一半时间通过的路程为t1v1,后一半时间通过的路程为t1v2,则有:st1v1t1v2,t1;
乙前一半路程所用时间为,后一半路程所用时间为,
则有:t2,
则t2﹣t10;
故t2>t1,即甲车用的时间少,即甲车先到达,故A正确,B、C、D错误。
故选:A。
6.解:(1)物体在5s内的速度变化量△v=v1﹣v0=6m/s﹣2m/s=4m/s;
则物体的加速度大小:a0.8m/s2;
(2)由加速度的定义可知:a,
由题意可知,图乙中阴影部分的面积表示做匀加速直线运动的物体速度由v0到v1,运动时间为t通过的路程,且图乙中阴影部分的面积等于长方形的面积和三角形的面积之和,
则物体通过的路程:s=S长方形+S三角形=v0t(v1﹣v0)t=v0tt2=v0tat2。
故答案为:(1)0.8;(2)v0tat2。
【密度、压强和浮力】
1.解:A、两个完全相同的量筒分别盛有质量相等的水和煤油,所以两个容器底面受到的液体压力相等且等于液体的重力,所以压强相等,故A不符合题意;
B、A、B两点到液面的距离相等即同深度,利用压强计算公式p=ρgh可知,由于水的密度大于煤油的密度,所以,A点的压强大于B点的压强,故B不符合题意;
CD、A、C两点到容器底面的距离相等,煤油的密度小于水的密度,根据公式p=ρgh可知,A、C点以下部分的液体产生的压强是水中的压强大,煤油中的压强小。又因为两只量筒中液体对底面的压强相等,总压强减去A、C点以下部分的压强就等于A、C点以上部分产生的压强,因此可得出,A点的压强小于C点的压强。故C不符合题意,D符合题意。
故选:D。
2.解:(1)图甲中:由于冰块都处于漂浮状态,则:F甲浮=G冰,
根据阿基米德原理可得:F甲浮=ρAgV排甲,
所以,ρAgV排甲=G冰;
则:V排甲;
当冰全部熔化后由于冰的质量不变,即:G水=G冰,
则冰熔化后的水的体积为:V水;
由于ρA>ρ水,则:V排甲<V水,
所以,△V甲=V水﹣V排甲G冰;
图乙中:设冰块漂浮在水和液体A的冰块分为G1、G2;且G1+G2=G冰;
则由于冰块都处于漂浮状态,F水浮=G1;FA浮=G2;
根据阿基米德原理可得:F水浮=ρ水gV排水;FA浮=ρAgV排A;
则:ρ水gV排水=G1;ρAgV排A=G2;
所以,V排水,V排A;
则:V排乙=V排水+V排A;
当冰全部熔化后由于冰的质量不变,即:G水1=G1;G水2=G2;
则冰熔化后的水的体积为:V水乙=V水1+V水2
由于ρA>ρ水,则:V排乙<V水乙,
所以,△V乙=V水乙﹣V排乙()G2;
由于G1+G2=G冰;所以,△V甲>△V乙,
已知甲、乙两个完全相同的柱状容器。所以,根据h可知:
容器中液面升高的高度△h甲>△h乙;
由于冰块没有熔化前甲容器内液面和乙容器内液面恰好相平,所以,若冰块全部熔化后,甲容器内液面距离容器底部的高度h1大于乙容器内液面距离容器底部的高度h2;故BD错误;
(2)由于液体和水不相溶且ρA>ρ水,则冰熔化后,液体A会在容器的底部,由图可知:容器里液体A的体积关系是:V甲A>V乙A,由于甲乙容器完全相同,则根据h可知:
液体A的深度关系是:h1′>h2′,故A正确,C错误。
故选:A。
3.解:由图可知,A液体的体积要大于B液体的体积,液体A、B的质量相同,根据ρ可知,ρA<ρB;
容器为圆柱形容器,液体对容器底的压力F=G=mg,由于A液体的质量等于B液体的质量,所以A液体对容器底的压力等于B液体对容器底的压力;而两个圆柱形容器完全相同、底面积相同,所以由p可知A容器底受到的液体压强等于B容器底受到的液体压强;
将两个完全相同的金属球分别投入两容器中都浸没,且两容器均没有液体溢出,所以排开液体的体积相同,即液面升高的高度相同;
根据液体压强的公式p=ρgh可知,ΔpA=ρAgΔh,ΔpB=ρBgΔh,由于ρA<ρB,则ΔpA<ΔpB,所以将两个完全相同的金属球分别投入两容器中时,容器底部受到的压强关系为:pA<pB;
根据题意可知,容器质量相同、液体质量相同、小球质量相同,则两个容器的总质量相同,由G=mg可知,两容器的总重力相同,都在水平面上,容器对水平面的压力等于其重力,故压力相同,即,FA=FB。
故答案为:<;=。
4.解:设木棒长度为h,底面积为S,密度计重力为G,小滨将该密度计放入酒精中,密度计静止时L1为6cm,ρ酒精=0.8g/cm3=0.8×103kg/m3,
由F浮酒精=G,可得:ρ酒精gV排酒精=G,
即[(h﹣0.06m)S]×0.8×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣①,
小滨将该密度计放入水中,密度计静止时L2为8cm,由于水的密度ρ水=1.0g/cm3=1.0×103kg/m3,则与水面相对应的刻度线上应标记1.0g/cm3。
由F浮水=G,可得:
[(h﹣0.08m)S]×1.0×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣②,
由①②可得,h=0.16m;
设该密度计上对应密度值为1.25g/cm3的刻度线到密度计顶端的距离为L′,
则[(h﹣L′)S]×1.25×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣③,
将h=0.16m分别代入②和③,并将②③联立,
解得L=0.096m=9.6cm;
当密度计漂浮在密度为ρ液的液体中时,
因密度计始终漂浮,受到的浮力和自身的重力相等,
所以,G=F浮液,即ρgSh=ρ液gSh液,
整理可得:h液h,
由表达式可知,h液和ρ液是反比例函数,所以这种密度计的刻度是不均匀。
故答案为:1.0;9.6;不均匀,由表达式h液h可知,h液和ρ液是反比例函数。
5.解:
(1)木块漂浮,根据浮沉条件可知,F浮=G木,
根据阿基米德原理可知:F浮=ρ水V排g,木块的重力为:G木=ρ木V木g,
则:ρ水V排g=ρ木V木g,
木块总体积的露出水面,所以V排V木,
木块的密度为:ρ木ρ水1×103kg/m3=0.75×103kg/m3;
(2)如图:
当细绳断裂时,F浮′+F最大=G木,
设此时木块排开水的体积为V排′,则:
ρ水V排′g+F最大=ρ木V木g,
即:1×103kg/m3×V排′×10N/kg+4N=0.75×103kg/m3×(0.1m)3×10N/kg,
解得:
V排′=3.5×10﹣4m3;
(3)在细绳断开后木块再次漂浮时,浮力增加4N,排开水体积增加:
△V排4×10﹣4m3,
水面上升:
△h0.01m,
△p=ρg△h=1×103kg/m3×10N/kg×0.01m=100Pa。
即:容器底受水的压强增大了100Pa。
答:(1)木块的密度为0.75×103kg/m3;
(2)当细绳断裂前一瞬间关闭阀门,此时木块排开水的体积为3.5×10﹣4m3;
(3)在细绳断开后木块再次漂浮时,容器底受到水的压强与断绳前的瞬间相比,容器底受水的压强增大了100Pa。
【杠杆的动态平衡】
1.解:
(1)木条受到竖直向下的重力和支架对木条竖直向上的支持力,由二力平衡,G=FA+FB,
两支架对木条的支持力和木条对托盘的压力为作用力和反作用力,大小相等,故木棒的重力为:
G=3N+8N=11N;
(2)O为木条的重心,若向右移动甲台秤,使C点放在甲的支架上,以B为支点,木条的重力G为阻力,C点对木条的支持力FC为动力,杠杆的示意图如图1所示:
由杠杆的平衡条件,G×LB=FC×(LC+LB),
因G和LB不变,当向右移动甲台秤,使C点放在甲的支架上,LC变小,故动力臂变小,故FC变大,因乙台秤示数等于木条的重力与甲台秤示数,故则乙的示数变小;
设甲台秤支架到木条B端的距离为x,甲台秤的示数为F,
由杠杆的平衡条件,G×LB=F×x,
故F,因G与LB都不变,为一常数,故F与x为反比例函数,如下图2所示:
故答案为:(1)11N;(2)变小;如图2所示。
2.解:动力F的方向始终与杆垂直,故动力臂不变;
阻力是柱形物体的重,阻力作用点在柱形物体的重心上;
如下图所示(只画了杠杆的右侧部分,图中虚线为重心运动的路线):
0位置为原来的位置,1位置为阻力臂最大的位置,2位置为转过45°的位置,
由上图可知,整个过程中阻力臂先变大后变小;
因动力臂不变,阻力G不变,阻力臂先变大后变小,由杠杆平衡条件可知,动力F先增大后减小。
故答案为:先增大后减小。
3.解:
(1)由题只知道动力的作用点在B点,不知道动力的作用方向,所以也就不知道动力臂的大小,所以也就无法比较动力臂和阻力臂的大小关系,所以无法确定它是哪种杠杆;
(2)若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,此过程中,阻力和动力臂不变,阻力臂逐渐减小,根据杠杆的平衡条件可知动力变小;
(3)如图所示,
由图可知,当F丙由竖直向上的位置沿逆时针方向缓慢的转到水平向左的位置时,动力臂先变大后变小,阻力与阻力臂不变,由杠杆平衡条件可知,动力先变小后变大。且上图可以看出,F丙水平时,比F垂直OA时力臂小,所以动力更大。
动力F丙随时间t的变化趋势如图所示:
故答案为:不一定;变小;见上图。
4.解:(1)延长F2作用线,由支点作其作用线的垂线,L2是其力臂。如图:
(2)由图可知:当α角增大时,力臂L2变小;由于拉力F1的方向与脊柱夹角始终为12°,且OA这段距离不变,则O点到F1作用线的距离不变,即动力臂不变,阻力为箱子的重力不变,根据杠杆平衡条件可知,F1变小;
(3)如果考虑到人上半身的重力,由于上半身的重力会阻碍杠杆的转动,根据杠杆平衡条件可知:实际拉力将变大;
(4)比较甲、乙两种姿势可知:甲的支点太高,在搬起物体时,阻力臂减小得慢,则腰背部复杂肌肉的等效拉力F1要比较长时间的使用较大的力,所以甲姿势不正确,乙姿势比较正确。
故答案为:(1)如上图;(2)变小;变小;(3)大;(4)乙
力学
同课章节目录
