3.2.1单调性与最大(小)值-第一课时-高中数学人教A版必修一同步课件(共25张PPT)
文档属性
| 名称 | 3.2.1单调性与最大(小)值-第一课时-高中数学人教A版必修一同步课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 16.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 12:22:50 | ||
图片预览






文档简介
(共25张PPT)
数 学
数 学
题型一 判断或证明函数的单调性
知识梳理
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂精炼
数 学
题型二 求函数的单调区间
知识梳理
课堂精讲
课堂精讲
课堂精讲
课堂精讲
课堂精炼
数 学
题型三 函数单调性的简单应用
知识梳理
课堂精讲
课堂精讲
课堂精讲
警示:
千万注意不要忽视函数的定义域。
课堂精讲
课堂精讲
课堂精炼
课堂小结
2
1孤度
0
A
X
等
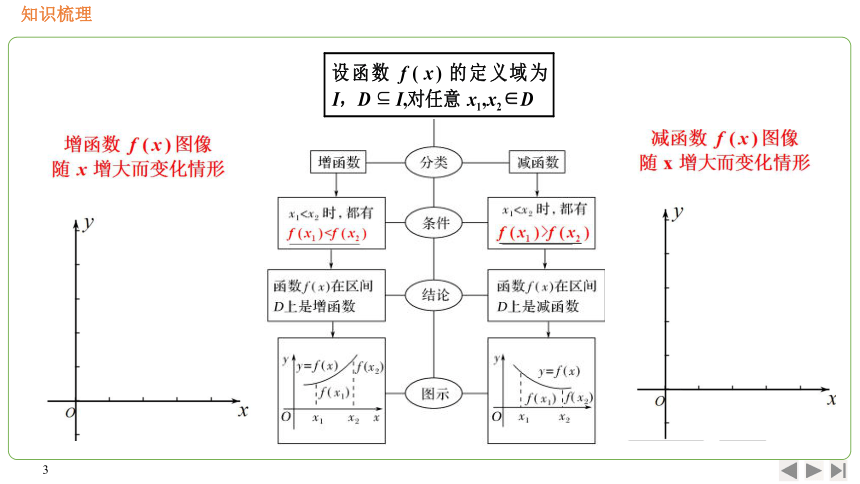
增函数f(x)图像
随x增大而变化情形
减函数f(x)图像
随x增大而变化情形
X
1
2X
f(x)=x2-1的图像
1
1
-1
1
2X
I
f()=,
的图像
x2_1
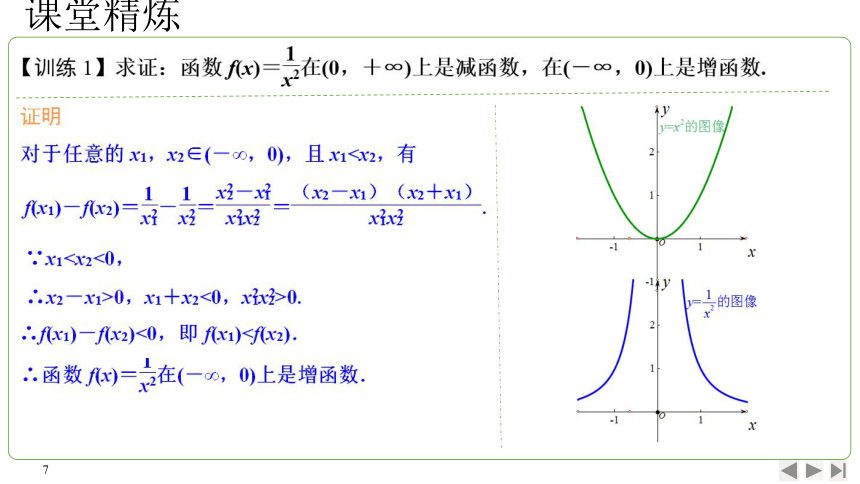
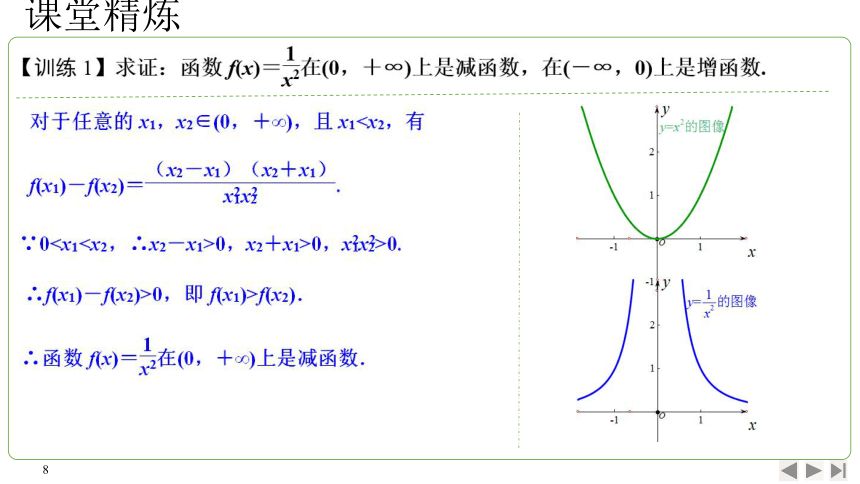
利用定义证明函数单调性的步骤:
(1)取值:设x1,x2是该区间内的任意两个值,且x1(2)作差变形:作差f)一fx2),并通过因式分解、通分、配方、有理化等手段,
转化为易判断正负的关系式;
(3)定号:确定fx1)一fx2)的符号;
〔4)结论:根据fx)一fx2)的符号与定义确定单调性.
y
x的图像
2
-1
1
X
=1
的图像
2
1
-1
1
2.函数的单调区间
单调区间一般用“,”或“和”连接
如果函数y=fx)在区间D上是
那么就说函数y=x)在这
区间具有
区间D叫做y=fx)的单调区间.
3.有关单调性的常用结论记住这些结论有利于快速解题
在公共定义域内,增函数十增函数=
;减函数十减函数=;增函
数一减函数=
;减函数一增函数=
5
4
3
2
1
X
4321
1234
先做y=x24x+3(x>0)的图像
J)
4
3
2
1
x
-4-3
-2
21
O
1
3
4
5
-1
f(x)=x2一4+3的图像
1.求函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等
可根据其单调性写出函数的单调区间,若函数不是上述函数且函数图象容易作
出,可作出其图象,根据图象写出其单调区间.
2.一个函数出现两个或两个以上的单调区间时,不能用“U连接两个单调区间,
而要用“和”或6,”连接.
【训练2】(1)(多空题)如图所示的是定义在区间[一5,5]上的函数y=fx)的图
象,则函数的单调递减区间是
,在区间
上是增函数
↑
3
-2
231
y=f(x)
I
(3w-1)x+4,
1
0
I
1
y=-比
-XⅪ-6--
-1
1
1
2
x
83
1
1
a=-0.099
-1H
1
(3-1)1+4-…
1
数 学
数 学
题型一 判断或证明函数的单调性
知识梳理
课堂精讲
课堂精讲
课堂精讲
课堂精炼
课堂精炼
数 学
题型二 求函数的单调区间
知识梳理
课堂精讲
课堂精讲
课堂精讲
课堂精讲
课堂精炼
数 学
题型三 函数单调性的简单应用
知识梳理
课堂精讲
课堂精讲
课堂精讲
警示:
千万注意不要忽视函数的定义域。
课堂精讲
课堂精讲
课堂精炼
课堂小结
2
1孤度
0
A
X
等
增函数f(x)图像
随x增大而变化情形
减函数f(x)图像
随x增大而变化情形
X
1
2X
f(x)=x2-1的图像
1
1
-1
1
2X
I
f()=,
的图像
x2_1
利用定义证明函数单调性的步骤:
(1)取值:设x1,x2是该区间内的任意两个值,且x1
转化为易判断正负的关系式;
(3)定号:确定fx1)一fx2)的符号;
〔4)结论:根据fx)一fx2)的符号与定义确定单调性.
y
x的图像
2
-1
1
X
=1
的图像
2
1
-1
1
2.函数的单调区间
单调区间一般用“,”或“和”连接
如果函数y=fx)在区间D上是
那么就说函数y=x)在这
区间具有
区间D叫做y=fx)的单调区间.
3.有关单调性的常用结论记住这些结论有利于快速解题
在公共定义域内,增函数十增函数=
;减函数十减函数=;增函
数一减函数=
;减函数一增函数=
5
4
3
2
1
X
4321
1234
先做y=x24x+3(x>0)的图像
J)
4
3
2
1
x
-4-3
-2
21
O
1
3
4
5
-1
f(x)=x2一4+3的图像
1.求函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等
可根据其单调性写出函数的单调区间,若函数不是上述函数且函数图象容易作
出,可作出其图象,根据图象写出其单调区间.
2.一个函数出现两个或两个以上的单调区间时,不能用“U连接两个单调区间,
而要用“和”或6,”连接.
【训练2】(1)(多空题)如图所示的是定义在区间[一5,5]上的函数y=fx)的图
象,则函数的单调递减区间是
,在区间
上是增函数
↑
3
-2
231
y=f(x)
I
(3w-1)x+4,
1
0
I
1
y=-比
-XⅪ-6--
-1
1
1
2
x
83
1
1
a=-0.099
-1H
1
(3-1)1+4-…
1
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
