2023年河南省洛阳市中考数学仿真模拟试卷(含答案)
文档属性
| 名称 | 2023年河南省洛阳市中考数学仿真模拟试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 405.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 22:19:21 | ||
图片预览


文档简介
2023年河南省洛阳市中考数学 仿真 模拟试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列实数中最大的是( )
A. B. C. D.
2. 一种变异的新冠病毒有包膜呈圆形,其直径约纳米纳米米,将纳米用科学记数法表示为( )
A. 米 B. 米 C. 米 D. 米
3. 如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“梦”字一面的相对面上的字是( )
A. 代 B. 中 C. 国 D. 新
4. 如图,点在直线上,,若,则的大小( )
A.
B.
C.
D.
5. 已知,两点在双曲线上,且,则的取值范围是( )
A. B. C. D.
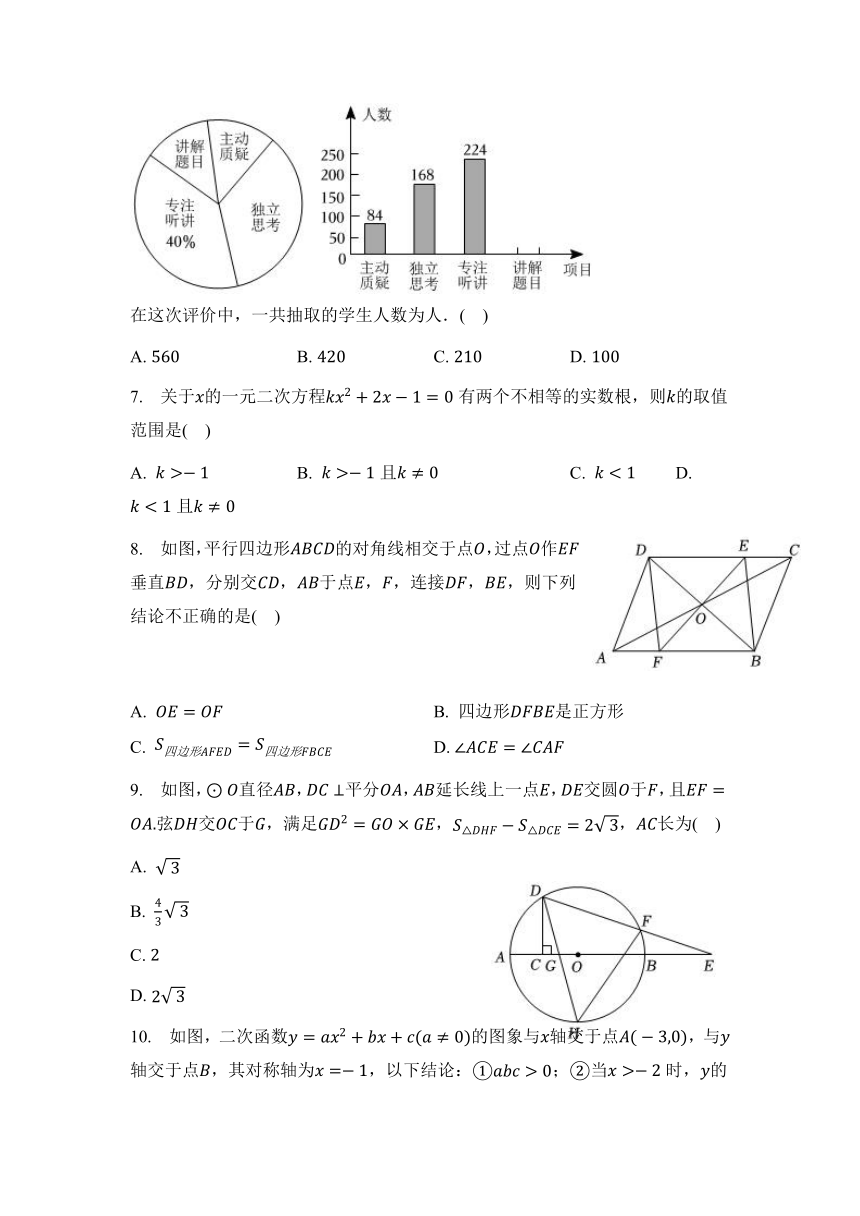
6. 某校九年级教师对第一轮复习进行评价调查,评价组随机抽取了若干名学生的参与情况,绘制成如图所示的条形统计图和扇形统计图均不完整,请根据图中所给信息解答下列问题:
在这次评价中,一共抽取的学生人数为人.( )
A. B. C. D.
7. 关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. 且 C. D. 且
8. 如图,平行四边形的对角线相交于点,过点作垂直,分别交,于点,,连接,,则下列结论不正确的是( )
A. B. 四边形是正方形
C. D.
9. 如图,直径,平分,延长线上一点,交圆于,且弦交于,满足,,长为( )
A.
B.
C.
D.
10. 如图,二次函数的图象与轴交于点,与轴交于点,其对称轴为,以下结论:;当时,的值随值的增大而增大;;抛物线一定经过点;关于的方程有两个不相等的实数根其中正确结论的个数是( )
A. 个
B. 个
C. 个
D. 个
二、填空题(本大题共5小题,共15.0分)
11. 若不等式组的解集为,则 ______ .
12. 为了响应国家“双减”政策,某校在课后延时服务时段新开发了器乐、戏曲、棋类三大类兴趣课程,现学校从这三类课程中随机抽取两类参加“全市青少年才艺展示活动”,则恰好抽到“戏曲”和“棋类”的概率______ .
13. 如图,在中,和的平分线相交于点,过作,交于点,交于点,若,,则线段的长为______ .
14. 如图,矩形中,,点为上一点,将沿着翻折得到,恰有,且,则的长为 ,的值为 .
15. 如图,矩形的顶点,分别在轴、轴上,点的坐标为,是的内切圆,点,点分别是,轴上的动点,则的最小值是______ .
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
16. 分
计算:
先化简,再求值:,其中.
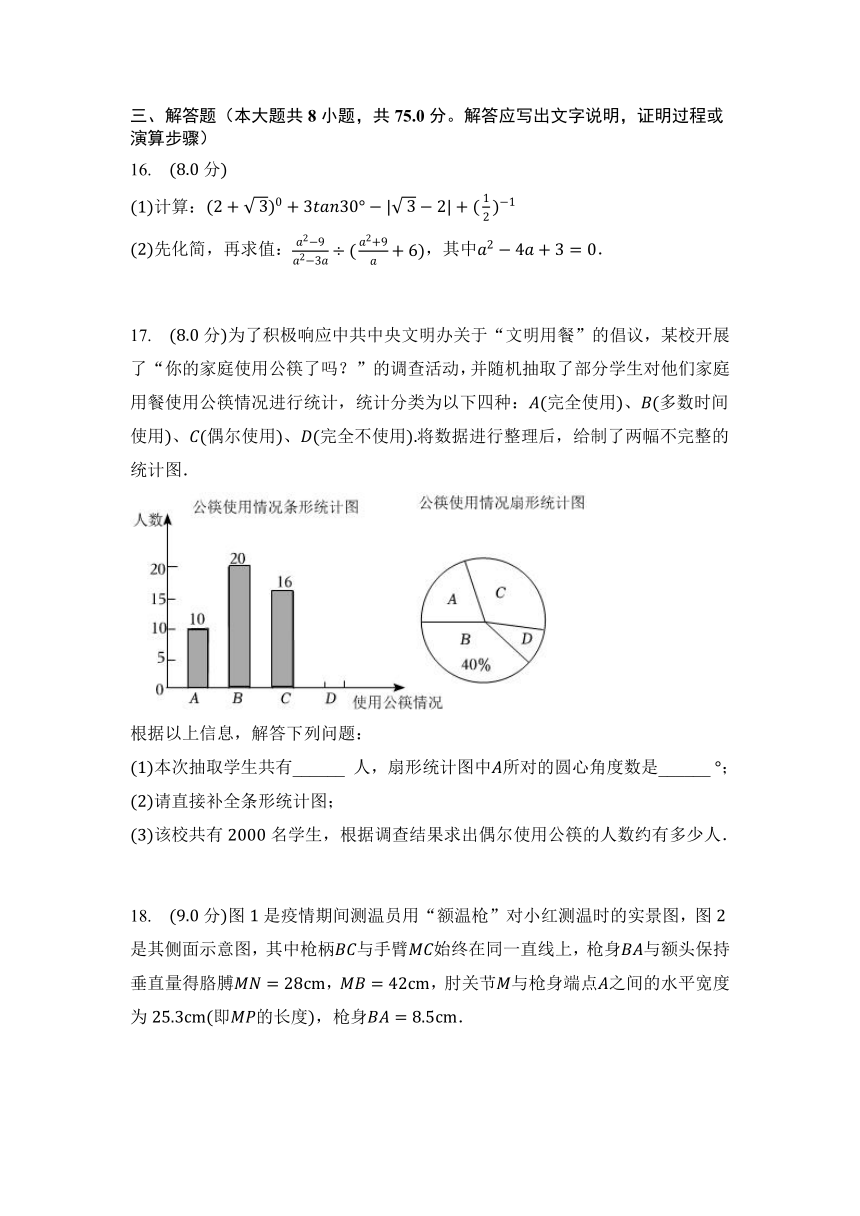
17. 分为了积极响应中共中央文明办关于“文明用餐”的倡议,某校开展了“你的家庭使用公筷了吗?”的调查活动,并随机抽取了部分学生对他们家庭用餐使用公筷情况进行统计,统计分类为以下四种:完全使用、多数时间使用、偶尔使用、完全不使用将数据进行整理后,给制了两幅不完整的统计图.
根据以上信息,解答下列问题:
本次抽取学生共有______ 人,扇形统计图中所对的圆心角度数是______ ;
请直接补全条形统计图;
该校共有名学生,根据调查结果求出偶尔使用公筷的人数约有多少人.
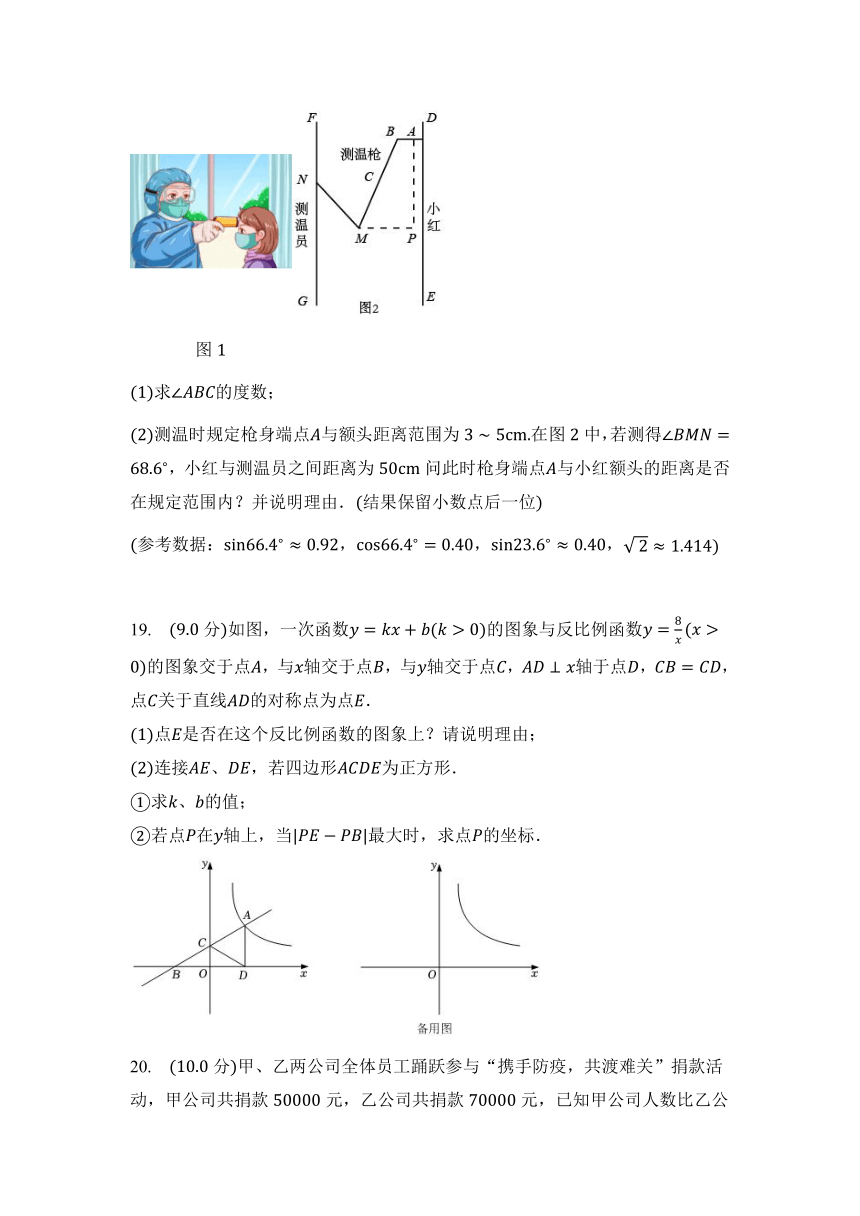
18. 分图是疫情期间测温员用“额温枪”对小红测温时的实景图,图是其侧面示意图,其中枪柄与手臂始终在同一直线上,枪身与额头保持垂直量得胳膊,,肘关节与枪身端点之间的水平宽度为即的长度,枪身.
图
求的度数;
测温时规定枪身端点与额头距离范围为在图中,若测得,小红与测温员之间距离为问此时枪身端点与小红额头的距离是否在规定范围内?并说明理由.结果保留小数点后一位
参考数据:,,,
19. 分如图,一次函数的图象与反比例函数的图象交于点,与轴交于点,与轴交于点,轴于点,,点关于直线的对称点为点.
点是否在这个反比例函数的图象上?请说明理由;
连接、,若四边形为正方形.
求、的值;
若点在轴上,当最大时,求点的坐标.
20. 分甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款元,乙公司共捐款元,已知甲公司人数比乙公司少人,乙公司的人均捐款是甲公司人均捐款的倍
求甲、乙两公司各有多少人?
现用所有捐款购买,两种防疫物资,已知种防疫物资每箱元,种防疫物资每箱元,若购买种防疫物资不少于箱,问有几种购买方案?请设计出来注:,两种防疫物资都要购买,且只能整箱买,所有捐款要恰好用完
21. 分如图,内接于,,过点的切线与的延长线相交于点.
求证:;
若,求阴影部分的面积.
22. 分如图,灌溉车为绿化带浇水,喷水口离地竖直高度为可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形,其水平宽度,竖直高度下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点离喷水口的水平距离为,高出喷水口,灌溉车到绿化带的距离为单位:.
求上边缘抛物线的函数解析式,并求喷出水的最大射程;
求下边缘抛物线与轴的正半轴交点的坐标;
要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出的取值范围.
23. 分如图,在矩形中,其中,点是边上一动点点不与重合,点是边的中点,连接,将矩形沿直线进行翻折,其顶点翻折后的对应点为,连接并延长,交边于点点不与重合,过点作的平分线,交矩形的边于点.
求证:;
如图,在点运动过程中,若,,三点在同一条直线上时,点与点刚好重合,求的值;
若,连接,,当是以为直角边的直角三角形时,求的值.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.解:原式
;
原式
,
,
,
或,
又,
,,,
当时,
原式.
17.解:(1)本次抽取的学生总人数共有:20÷40%=50(人),
扇形统计图中A所对的圆心角度是:,
故答案为:50,72;
(2)D的人数为:50-10-20-16=4(人),
条形统计图补全如下:
(3)由题意得(人),
答:估计偶尔使用公筷的人数是640人.
18.解:过作于点,由题意可知四边形为矩形,
,
在中,
,
,
,
,
答:的度数为;
延长交于点,由题意得:,
,,
,
在中,
,
,
枪身端点与小红额头的距离为,
,
枪身端点与小红额头的距离在规定范围内.
19.解:点在这个反比例函数的图象上,
理由:一次函数的图象与反比例函数的图象交于点,
设点的坐标为,
点关于直线的对称点为点,
,平分,
如图,连接交于,
,
轴于,
轴,
,
,
点在这个反比例函数的图象上;
四边形为正方形,
,垂直平分,
,
设点的坐标为,
,,
,
负值舍去,
,,
把,代入得,
;
延长交轴于,
,,
点与点关于轴对称,
,则点即为符合条件的点,
由知,,,
,,
设直线的解析式为,
,,
直线的解析式为,
当时,,
.
故当最大时,点的坐标为.
20.解:设甲公司有人,
根据题意,得,
解得,
经检验,是原方程的根,且符合题意,
人,
答:甲公司有人,乙公司有人;
设购买种防疫物资箱,购买种防疫物资箱,
根据题意,得,
即,
购买种防疫物资不少于箱,,两种防疫物资都要购买,且只能整箱买,所有捐款要恰好用完,
满足条件的和的取值有:
或,
共有两种购买方案,
方案:购买种物资箱,种物资箱,
方案:购买种物资箱,种物资箱.
21.证明:,,,
≌,
,
,,
与圆相切于,
半,
;
解:,
,
,
,
,
,
,
,
,
,
,
,
是等腰直角三角形,
,
,
是等腰直角三角形,
,
扇形的面积,的面积,
阴影的面积的面积扇形的面积.
22.解:如图,由题意得是上边缘抛物线的顶点,
设,
又抛物线过点,
,
,
上边缘抛物线的函数解析式为,当时,,
解得,舍去,
喷出水的最大射程为;
解:对称轴为直线,
点的对称点为,
下边缘抛物线是由上边缘抛物线向左平移得到的,
点的坐标为;
解:,
点的纵坐标为,
,解得,
,
,
当时,随的增大而减小,
当时,要使,
则,
当时,随的增大而增大,且时,,
当时,要使,则,
,灌溉车行驶时喷出的水能浇灌到整个绿化带,
的最大值为,
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是,
的最小值为,
综上所述,的取值范围是.
23.证明:由翻折知,,
平分,
,
,
,
,
;
解:由翻折知,,,
,,三点在同一直线上,
,
又,,
≌,
,
是的中点,
设,
,
,
在中,由勾股定理得,
,
,
,
,
;
解:设,
,
,
若点在上,当时,
此时,
,
四边形为矩形,
,
矩形为正方形,
,
,
,
若点在上,当时,
此时,,三点在同一直线上,
过点作于点,
由可知,,,
,
,
;
若点在上,显然不能为直角,当时,
是角平分线,
,
又,,
≌,
,
如图,连接,
,,,
≌,
,
设,,
,
,
,,
,
,
,,
,
∽,
,
,
解得,
当时,在边上,
,
,
,
,
综上所述,的值为或或.
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列实数中最大的是( )
A. B. C. D.
2. 一种变异的新冠病毒有包膜呈圆形,其直径约纳米纳米米,将纳米用科学记数法表示为( )
A. 米 B. 米 C. 米 D. 米
3. 如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“梦”字一面的相对面上的字是( )
A. 代 B. 中 C. 国 D. 新
4. 如图,点在直线上,,若,则的大小( )
A.
B.
C.
D.
5. 已知,两点在双曲线上,且,则的取值范围是( )
A. B. C. D.
6. 某校九年级教师对第一轮复习进行评价调查,评价组随机抽取了若干名学生的参与情况,绘制成如图所示的条形统计图和扇形统计图均不完整,请根据图中所给信息解答下列问题:
在这次评价中,一共抽取的学生人数为人.( )
A. B. C. D.
7. 关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. 且 C. D. 且
8. 如图,平行四边形的对角线相交于点,过点作垂直,分别交,于点,,连接,,则下列结论不正确的是( )
A. B. 四边形是正方形
C. D.
9. 如图,直径,平分,延长线上一点,交圆于,且弦交于,满足,,长为( )
A.
B.
C.
D.
10. 如图,二次函数的图象与轴交于点,与轴交于点,其对称轴为,以下结论:;当时,的值随值的增大而增大;;抛物线一定经过点;关于的方程有两个不相等的实数根其中正确结论的个数是( )
A. 个
B. 个
C. 个
D. 个
二、填空题(本大题共5小题,共15.0分)
11. 若不等式组的解集为,则 ______ .
12. 为了响应国家“双减”政策,某校在课后延时服务时段新开发了器乐、戏曲、棋类三大类兴趣课程,现学校从这三类课程中随机抽取两类参加“全市青少年才艺展示活动”,则恰好抽到“戏曲”和“棋类”的概率______ .
13. 如图,在中,和的平分线相交于点,过作,交于点,交于点,若,,则线段的长为______ .
14. 如图,矩形中,,点为上一点,将沿着翻折得到,恰有,且,则的长为 ,的值为 .
15. 如图,矩形的顶点,分别在轴、轴上,点的坐标为,是的内切圆,点,点分别是,轴上的动点,则的最小值是______ .
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
16. 分
计算:
先化简,再求值:,其中.
17. 分为了积极响应中共中央文明办关于“文明用餐”的倡议,某校开展了“你的家庭使用公筷了吗?”的调查活动,并随机抽取了部分学生对他们家庭用餐使用公筷情况进行统计,统计分类为以下四种:完全使用、多数时间使用、偶尔使用、完全不使用将数据进行整理后,给制了两幅不完整的统计图.
根据以上信息,解答下列问题:
本次抽取学生共有______ 人,扇形统计图中所对的圆心角度数是______ ;
请直接补全条形统计图;
该校共有名学生,根据调查结果求出偶尔使用公筷的人数约有多少人.
18. 分图是疫情期间测温员用“额温枪”对小红测温时的实景图,图是其侧面示意图,其中枪柄与手臂始终在同一直线上,枪身与额头保持垂直量得胳膊,,肘关节与枪身端点之间的水平宽度为即的长度,枪身.
图
求的度数;
测温时规定枪身端点与额头距离范围为在图中,若测得,小红与测温员之间距离为问此时枪身端点与小红额头的距离是否在规定范围内?并说明理由.结果保留小数点后一位
参考数据:,,,
19. 分如图,一次函数的图象与反比例函数的图象交于点,与轴交于点,与轴交于点,轴于点,,点关于直线的对称点为点.
点是否在这个反比例函数的图象上?请说明理由;
连接、,若四边形为正方形.
求、的值;
若点在轴上,当最大时,求点的坐标.
20. 分甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款元,乙公司共捐款元,已知甲公司人数比乙公司少人,乙公司的人均捐款是甲公司人均捐款的倍
求甲、乙两公司各有多少人?
现用所有捐款购买,两种防疫物资,已知种防疫物资每箱元,种防疫物资每箱元,若购买种防疫物资不少于箱,问有几种购买方案?请设计出来注:,两种防疫物资都要购买,且只能整箱买,所有捐款要恰好用完
21. 分如图,内接于,,过点的切线与的延长线相交于点.
求证:;
若,求阴影部分的面积.
22. 分如图,灌溉车为绿化带浇水,喷水口离地竖直高度为可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形,其水平宽度,竖直高度下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点离喷水口的水平距离为,高出喷水口,灌溉车到绿化带的距离为单位:.
求上边缘抛物线的函数解析式,并求喷出水的最大射程;
求下边缘抛物线与轴的正半轴交点的坐标;
要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出的取值范围.
23. 分如图,在矩形中,其中,点是边上一动点点不与重合,点是边的中点,连接,将矩形沿直线进行翻折,其顶点翻折后的对应点为,连接并延长,交边于点点不与重合,过点作的平分线,交矩形的边于点.
求证:;
如图,在点运动过程中,若,,三点在同一条直线上时,点与点刚好重合,求的值;
若,连接,,当是以为直角边的直角三角形时,求的值.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.解:原式
;
原式
,
,
,
或,
又,
,,,
当时,
原式.
17.解:(1)本次抽取的学生总人数共有:20÷40%=50(人),
扇形统计图中A所对的圆心角度是:,
故答案为:50,72;
(2)D的人数为:50-10-20-16=4(人),
条形统计图补全如下:
(3)由题意得(人),
答:估计偶尔使用公筷的人数是640人.
18.解:过作于点,由题意可知四边形为矩形,
,
在中,
,
,
,
,
答:的度数为;
延长交于点,由题意得:,
,,
,
在中,
,
,
枪身端点与小红额头的距离为,
,
枪身端点与小红额头的距离在规定范围内.
19.解:点在这个反比例函数的图象上,
理由:一次函数的图象与反比例函数的图象交于点,
设点的坐标为,
点关于直线的对称点为点,
,平分,
如图,连接交于,
,
轴于,
轴,
,
,
点在这个反比例函数的图象上;
四边形为正方形,
,垂直平分,
,
设点的坐标为,
,,
,
负值舍去,
,,
把,代入得,
;
延长交轴于,
,,
点与点关于轴对称,
,则点即为符合条件的点,
由知,,,
,,
设直线的解析式为,
,,
直线的解析式为,
当时,,
.
故当最大时,点的坐标为.
20.解:设甲公司有人,
根据题意,得,
解得,
经检验,是原方程的根,且符合题意,
人,
答:甲公司有人,乙公司有人;
设购买种防疫物资箱,购买种防疫物资箱,
根据题意,得,
即,
购买种防疫物资不少于箱,,两种防疫物资都要购买,且只能整箱买,所有捐款要恰好用完,
满足条件的和的取值有:
或,
共有两种购买方案,
方案:购买种物资箱,种物资箱,
方案:购买种物资箱,种物资箱.
21.证明:,,,
≌,
,
,,
与圆相切于,
半,
;
解:,
,
,
,
,
,
,
,
,
,
,
,
是等腰直角三角形,
,
,
是等腰直角三角形,
,
扇形的面积,的面积,
阴影的面积的面积扇形的面积.
22.解:如图,由题意得是上边缘抛物线的顶点,
设,
又抛物线过点,
,
,
上边缘抛物线的函数解析式为,当时,,
解得,舍去,
喷出水的最大射程为;
解:对称轴为直线,
点的对称点为,
下边缘抛物线是由上边缘抛物线向左平移得到的,
点的坐标为;
解:,
点的纵坐标为,
,解得,
,
,
当时,随的增大而减小,
当时,要使,
则,
当时,随的增大而增大,且时,,
当时,要使,则,
,灌溉车行驶时喷出的水能浇灌到整个绿化带,
的最大值为,
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是,
的最小值为,
综上所述,的取值范围是.
23.证明:由翻折知,,
平分,
,
,
,
,
;
解:由翻折知,,,
,,三点在同一直线上,
,
又,,
≌,
,
是的中点,
设,
,
,
在中,由勾股定理得,
,
,
,
,
;
解:设,
,
,
若点在上,当时,
此时,
,
四边形为矩形,
,
矩形为正方形,
,
,
,
若点在上,当时,
此时,,三点在同一直线上,
过点作于点,
由可知,,,
,
,
;
若点在上,显然不能为直角,当时,
是角平分线,
,
又,,
≌,
,
如图,连接,
,,,
≌,
,
设,,
,
,
,,
,
,
,,
,
∽,
,
,
解得,
当时,在边上,
,
,
,
,
综上所述,的值为或或.
同课章节目录
