下学期 高中数学知识梳理与解题指要[下学期]
文档属性
| 名称 | 下学期 高中数学知识梳理与解题指要[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 242.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-13 00:00:00 | ||
图片预览










文档简介
课件57张PPT。高中数学知识梳理
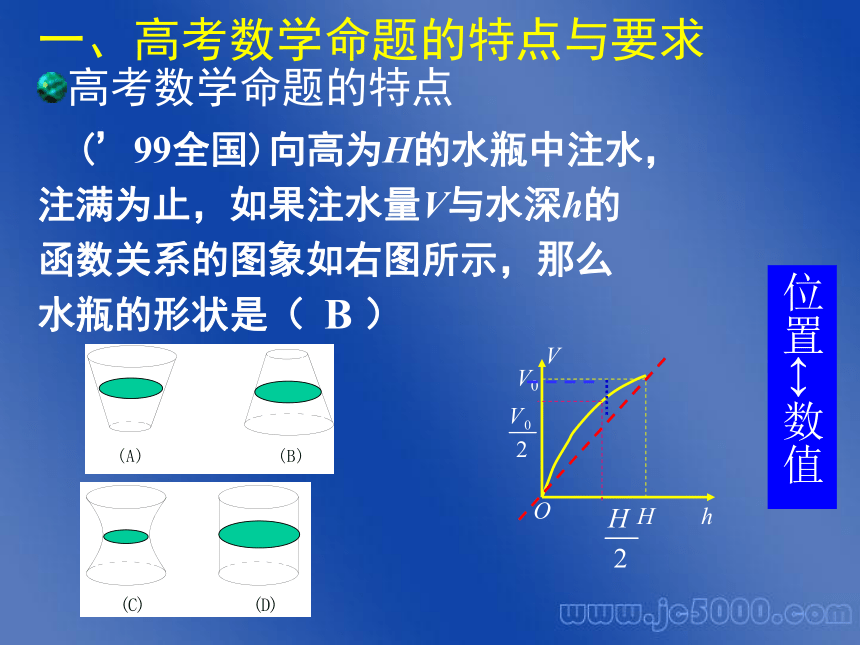
与解题指要 一、数学高考介绍二、数学知识梳理三、数学试题简析四、数学解题指要 (’99全国)向高为H的水瓶中注水,
注满为止,如果注水量V与水深h的
函数关系的图象如右图所示,那么
水瓶的形状是( )
一、高考数学命题的特点与要求高考数学命题的特点B 位置?数值 h H V V0 O f( )= = f ( x )+f ( )=1.(2002 全国)已知函数f (x)=
则 f( 1 )+f( 2 )+f( )+f( 3 )+f( )+f( 4 )+
f ( )= .结构特征 高考数学是考查数学基础的考试①基础知识
②基本技能
③基本数学思想方法
a、数形结合(转换策略)
b、函数与方程(分析策略)
c、分类讨论(分解策略)
d、等价转换(分析策略)
①在高考数学命题中,经历了“以知识立意”到以“问题立意”,再发展为“以能力立意”的过程。
②以能力立意命题,保障了高考突出能力与学习 潜能考查的要求。
③以能力立意命题拓展了命题思路。
④以能力立意命题于题型设计,易于形成综合自 然、新颖脱俗的试题。
⑤以能力立意命题在全卷的整合时,对试题的整体布局、层次安排有高屋建瓴之势。。
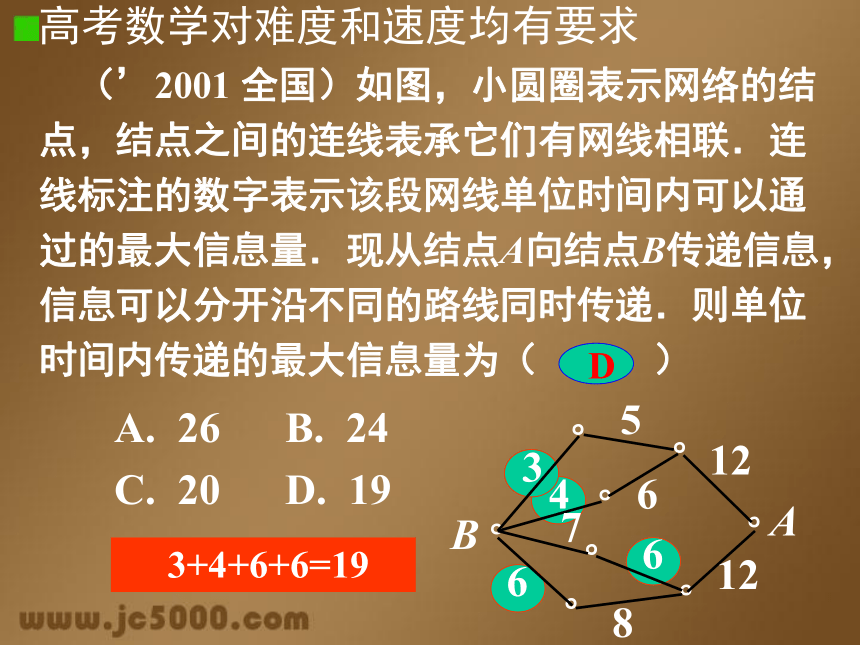
⑥以能力立意命题促进了高考改革的深入发展。高考数学注重能力考查 3+4+6+6=19高考数学对难度和速度均有要求 木 桶 原 理知识要求
①了解
②理解和掌握
③灵活和综合运用
能力要求
①思维能力
②运算能力
③空间想像能力
④实践能力
⑤创新意识
个性品质要求高考数学的要求二、高考数学知识梳理与复习高考数学知识梳理 平面向量 ①理解向量的概念,掌握向量的几何表, 了解共线向量的概念。②掌握向量的加法与减法。 ③掌握实数与向量的积,理解两个向量 共线的充要条件。④了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。
⑤掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件。
⑥掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用、掌握平移公式。①理解集合、子集、补集、交集、并集的 概念。了解空集和全集的意义。了解属 于、包含、相等关系的意义。掌握有关 的术语和符号,并会用它们正确表示一 些简单的集合。
②理解逻辑联结词“或”、“且”、“非” 的含义。理解四种命题及其相互关系,掌 握充分条件、必要条件及充要条件的意 义。集合、简易逻辑函数①了解映射的概念,理解函数的概念。
②了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法。
③了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数。
④理解分数指数幂的概念,掌握有理指数幂的运算性质。掌握指数函数的概念、图象和性质⑤理解对数的概念,掌握对数的运算性质, 掌握对数函数的概念、图像和性质。
⑥能够运用函数的性质、指数函数和对数函 数的性质解决某些简单的实际问题。 ①理解不等式的性质及其证明。
②掌握两个(不扩展到三个)正数的算术 平均数不小于它们的几何平均数的定 理,并会简单的应用。
③掌握分析法、综合法、比较法证明简单 的不等式。
④掌握简单不等式的解法。
⑤理解不等式
∣a∣- ∣ b∣≤∣a+b∣≤∣a∣+∣b∣不等式①理解任意角的概念、弧度的意义,能正 确地进行弧度与角度的换算。
②掌握任意角的正弦、余弦、正切的定 义。了解余切、正割、余割的定义 ,掌 握同角三角函数的基本关系式: sin2α+cos2α=1, ,tanαcotα=1。 掌握正弦、余弦的诱导公式。了解周期 函数与最小正周期的意义。
③掌握两角和与两角差的正弦、余弦、正切 公式。掌握二倍角的正弦、余弦、正切公式。三角函数④能正确运用三角公式,进行简单的三角函 数式的化简、求值和恒等式证明。
⑤了解正弦函数、余弦函数、正切函数的图 像和性质,会用“五点法”画正弦函数、 余弦函数和函数y=Asin(ωx+ψ)的简图, 理解A、ω、ψ的物理意义。
⑥会由已知三角函数值求角,并会用符号 arcsinx、arccosx、arctanx表示。
⑦掌握正弦定理、余弦定理,并能初步运用 它们解斜三角形。①理解数列的概念,了解数列通项公式的 意义,了解递推公式是给出数列的一种 方法,并能根据递推公式写出数列的前 几项。
②理解等差数列的概念,掌握等差数列的 通项公式与前n项和公式,并能解决简单 的实际问题。
③理解等比数列的概念,掌握等比数列的 通项公式与前n项和公式,并能解决简单 的实际问题。数列①理解直线的倾斜角和斜率的概念,掌握过 两点的直线的斜率公式。掌握直线方程的 点斜式、两点式、一般式,并能根据条件 熟练地求出直线方程。
②掌握两条直线平行与垂直的条件,两条直 线所成的角和点到直线的距离公式。能够 根据直线的方程判断两条直线的位置关 系。
③了解二元一次不等式表示平面区域。直线和圆的方程④了解线性规划的意义,并会简单的应用。
⑤了解解析几何的基本思想,了解坐标法。
⑥掌握圆的标准方程和一般方程,理解圆的 参数方程。①掌握椭圆的定义、标准方程和椭圆的简 单几何性质。理解椭圆的参数方程。
②掌握双曲线的定义、标准方程和双曲线
的简单几何性质。
③掌握抛物线的定义、标准方程和抛物线 的简单几何性质。
④了解圆锥曲线的初步应用。圆锥曲线方程①掌握平面的基本性质,会作斜二测的画 法画水平放置的平面图形的直观图;能 够画出空间两条直线、直线和平面的各 种益关系的图形,能够根据图形想像它 们的位置关系。
②掌握直线和平面平行的判定定理和性质 定理;掌握直线和平面垂直的判定定 理;掌握三垂线定理及其逆定理。
③理解空间向量的概念,掌握空间向量的 加法、减法和数乘。直线、平面、简单几何体④了解空间向量的基本定理;理解空间向量 坐标的概念,掌握空间向量的坐标运算。
⑤掌握空间向量的数量积的定义及其性质; 掌握用直角坐标计算空间向量数量积的
公式;掌握空间两点间距离公式。
⑥理解直线的方向向量、平面的法向量、向 量在平面内的射影等概念。
⑦掌握直线和直线、直线和平面、平面和平 面所成的角、距离的概念。⑧了解多面体、凸多面体的概念,了解正多 面体的概念。
⑨了解棱柱的概念,掌握棱柱的性质,会画 直棱柱的直观图。
⑩了解棱锥的概念,掌握正棱锥的性质,会 画正棱锥的直观图。
11了解球的概念,掌握球的性质,掌握球的 表面积、体积公式○
①掌握分类计数原理与分步计数原理,并 能用它们分析和解决一些简单的应用问 题。
②理解排列的意义,掌握排列数计算公 式,并能用它解决一些简单的应用问题。
③理解组合的意义,掌握组合数计算公式和 组合数的性质,并能用它们解决一些简单 的应用问题。
④掌握二项式定理和二项展开式的性质,并 能用它们计算和证明一些简单的问题。排列、组合、二项式定理①了解随机事件的发生存在着规律性的随 机事件概率的意义。
②了解等可能性事件的概率的意义,会用 排列组合的基本公式计算一些等可能性 事件的概率。
③了解互斥事件与相互独立事件的意义, 会用互斥事件的概率加法公式与相互独 立事件的概率乘法公式计算一些事件的 概率。
④会计算事件在n次独立重复试验中恰好发 生k次概率。概率①了解随机抽样,了解分层抽样的意义, 会用它们对简单实际问题进行抽样。
②会用样本频率分布估计总体分布。
③会用样本估计总体期望值和方差。统计①了解导数概念的实际背景。
②理解导数的几何意义。
③掌握函数y=c(C为常数)、y=xn(n∈N+) 的导数公式,会求多项式函数的导数。
④理解极大值、极小值、最大值、最小值的 概念,并会用导数求多项式函数的单调区 间、极大值、极小值及闭区间上的最大值 和最小值。
⑤会利用导数求某些简单实际问题的最大 值和最小值。 导数设函数f(x)的导数为f ?(x), 且 f(x)=x3+2x f ?(1)
则 f ?(0)= ( ) A. 0 B. -3 C. -6 D. 6 理解 f ?(1)是常量 ∵ f ?(x)=3x2+2f ?(1), ∴ f ?(0)=2f ?(1). ① 又 f ?(1)=3+2f ?(1),∴ f ?(1)=-3.代入 ①式,得 f ?(0)=-6.高考复习“四字诀”②深层次挖掘教材
如:{an}为等差数列,a1、a2、a9成等比数列
则
题目的来源:选择特殊数列为背景,最常 见、最先想到的是自然数列,易知它满足条 件,所以选an=n。
再如函数这一部分,复习时可对y= 和 y=logax的图象和性质进行研究。广:天高任鸟飞 ①全面复习,知识和能力并重
②学会学习新:万变不离其宗
①“旧题”新解,追求优美
例如:过抛物线y2=x上一点(4,2),作倾
角互补的两条直线AB、AC交抛物线 B、C,求证:直线BC的斜率为定值。
思考: 按照与作图步骤相吻合的思路来求解。 解:设KAB=K,则,KAC=-K,AB的方程为 y=k(x-4)+2
因此,A(4,2),B(XB,YB)是方程组
可求得KBC=再思考:在解题过程中,求B点坐标的计算量比较 大,应该想办法改进。我们还再回顾一下原来的解题程序。
设KAB→写直线AB、AC的方程→解出B、C→表示KBC改进:先设B、C坐标。
改进后的程序为:
设B、C坐标→求出KAB、KAC→表示KBC
设B( ,t2),C( ,t2)(∣t1∣≠∣t2∣)
这时KAB= , KAC=
∵KAB=-KAC,即x0ABCy化简得:t1+2= -(t2+2)
下面怎么办?似乎迷失了方向。我们还是应该明确一下本题的目标。要证明KBC是一个定值,于是不妨先求出
KBC KBC=这就好了,原来是要证明t1+t2是定值。
这样,就自然想到将t1+2=-(t2+2)变形为 t1+t2= - 4
本题圆满获得解决。再改进:设B、C坐标→表示KBC→求出KAB、KAC②看透本质,新题通法。 “知识与技能”突出思想和智慧
程序性
主干性
这里的技能特性也有两点:
独立操作性:由重复再现过渡到独立 完成;
迁移性:通过联系的思想与转换的手 段达到灵活运用、举一反三和触类旁 通的目的。三、去年高考数学试题的亮点 例1 (高考第一题第6小题)某校为了了解学生的课外 阅读情况,随机调查了50名学生,得到他们在某 一天各自课外阅读所用时间的数据,结果用图形 表示,根据条形图可得这50名学生这一天平均每 人的课外阅读时间为
A、0.6小时
B、0.9小时
C、1.0小时
D、1.5小时
解析 一天平均每人课外阅读时间为
=0.9(小时)
故选B。时间(小时)
0 0.5 1.0 1.5 2.0 x
y
20
15
10
5
人数(人)
例2(高考第一题第8小题)设k>1,f(x)=k(x-1) (x∈R)。在平面直角坐标系xOy中,函数 y=f(x)的图象与x轴变于A点,它的反函数
y=f-1(x)的图象与y轴交于B点,并且这两个函
数的图象交于P点,已知四边形OAPB的面积是
3,则k等于( )
A、 3
B、
C、
D、0 1 A xy
1
Bp解析:依题意A(1,0),B(0,1), y=f(x)与y=f-1(x)的交点必在 直线y=x上。
由 y=k(x-1),
y=x
解得:x=
因为S四边形OAPB=2S△OPA=2· ∣OA∣·∣xp∣= =3,
所以k= 。
故此选B“过程与方法”重视价值和策略
例3 (高考第二题第16小题)平面向量a、b
中,已知a=(4,-3),∣b∣=1且a·b=5 则向量b= 。 [方法1] 设a与b夹角为θ。
则由a·b=5→∣a∣∣b∣cosθ=5
→5·1·cosθ=5
→cosθ=1
→θ=0o
所以b与a共线且方向相同,
b=( ,- )。解析 解决本题至少可从这样两个角度思考[方法2] 设b=(x,y)
x2+y2=1 x=
4x-3y=5 y= -
或利用直线4x-3y=5与圆x2+y2=1相切的特征,借助几何图形,利用几何方法,求得切点坐标为( ,- )
b=( ,- )则 →“情感、态度与价值观”体现感悟和动力
例4(高考第六大题)制订投资计划时, 不仅要考虑可能获得的盈利,而且要考 虑可能出现的亏损。
某投资人打算投资甲、乙两个项目,根 据预测,甲、乙项目可能的最大利率分别 为100%为50%,可能的最大亏损率分别为 30%和10%,投资人计划投资金额超过10 万元,要求确保可能的资金亏损不超过1.8 万元。问投资人对甲、乙两个项目各投资 多少万元,才能使可能的盈利最大?解析 设投资人分别用x万元,y万元投资甲、乙两个项目,由题意知
x+y≤10,
0.3X+0.1y≤1.8,
x≤0,
y≥0.
目标函数z=x+0.5y.
上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域。
作直线L:x+0.5y=0,并作平行于直线L的一组直线。
X+0.5y=z,z∈R,与可行域相交,其中有一条直线经过可行域上的M点,且与直线x+0.5y=0的距离最大,这里M点是直线x+y=10和0.3x+0.1y=1.8的交点。Y
18
10
0 6 10 x
0.3x+0.1y=1.8
x+0.5y=0M(4,6)
x+y=10L解方程组
x+y=10
0.3x+0.1y=1.8
得x=4,y=6
此时z=1×4+0.5×6=7(万元)
因为7>0,
所以x=4,y=6时z取最大值。
答:投资人用4万元投资甲项目、6万元投 资乙项目,才能在确保亏损不超过1.8 万元的前提下,使可能的盈利最大。多思善想
思联系,网络知识,夯实基础
例1 α、β是两个不同的平面,m、n是 平面α及β之外的两条不同直线,给 出四个论断:①m⊥n,②α⊥β, ③n⊥β,④m⊥α,以其中三个论 断作为条件,余下一个论断作为结 论,写出你认为正确的一个命题 。 四、高考数学复习解题指要思路1:题目结构中a、b、c具有轮换对称性, 可将右式分为三个部分,用综合法易证: (a+b), (b+c), (a+c),三式相加即得。 例2 已知a>0,b>0,c>0,求证:
(a+b+c)
思多解,多方出击,培养思维的发散性是三角函数的特殊值,联系三角知识,可从右边证到左边。
思路2:(a+b)=asin+bcos=sin(+φ)≤(a+c)≤三式相加即得。(b+c)≤ B
α
a
b
A c同理: ≥ (a+c)
三式相加即得。 思路3 观察左边三个根式,联系立几知识,它们 是以a、b、c为三度的长方体的三个面的对 角线长度,可构造长方体来证明,如图:
∣AB∣= ,
a+b=∣AB∣sinα+∣AB∣cosα
= (sinα+cosα)
= sin(α+ )
≤
所以 ≥ (a+b)思规律,找变化,触类旁通例3 试证以过椭圆的焦点的弦为直径的圆必 和椭圆相应的准线相离。
例4 已知异面直线a和b所成的角为50o,P为 空间任一定点,则P点且与a、b所成的角都是30o的直线有且仅有 ( )
A、1条 B、2条 C、3条 D、4条
在本题中50o和30o的设置对答案起着重要作用。因此,可通过改变50o和30o的大小来深化对这类题目的理解。(1)若将50o改为25o,其余条件不变,则答 案是 。
(2)若将50o改为65o,其余条件不变,则答 案 。
(3)若将30o改为70o,其余条件不变,则答 案是 。
(4)若将50o改为xo,30o改为yo,且答案为A, 则x、y的关系式为 ;若答案为B,则 x、y的关系为 ;若答案为C,则x、 y的关系为 ;若答案为D,则x、y的 关系为 。例5 求和S=(x+ )+(x2+ )+…+(xn+ )
错解:
S=(x+x2+x3+…+xn)+( + + …+ )
= +
这是应用等比数列求和公式时很容易出现的 问题,按照等比数列求和公式,当公式q是一个不确 定的数时,求其前n项和,则要考虑q=1,q≠1两种情 况,因此应分四种情形求解:(1)x=1,y≠1; (2)x≠1,y=1;(3)x=1,y=1;(4)x≠1,y≠1思错处,找错因,提高辨别解题错误的能力例6 过抛物线y2=2px(p>0)的焦点的一条直线和 这条抛物线相交于P1、P2两点,两个交点的 纵坐标分别为y1、y2,求证:y1y2=-p2
①已知条件不变时
a、求证:x1x2= ;
b、求焦点弦∣P1P2∣的长;
c、求△OP1P2的面积;
d、求焦点弦P1P2中点的轨迹方程;
e、求证 :
f、求证:以焦点弦为直径的圆必与准线 相切。 思演变,层层深入,提高应变能力②改成逆命题:一条直线与抛物线y2=2px(p>0) 相交于P1(x1,y1)、P2(x2,y2)两点,如果 满足y1y2=-p2(或x1x2= ),那么这条直线过 抛物线的焦点。
③已知条件不变,再附加条件“过P1、P2分别作x 轴的垂线,垂足为M1、M2”,求证: ∣OM1∣、∣OF∣、∣OM2∣成等比数列。
④已知条件不变,再附加条件“过焦点F,再作 一条与P1P2垂直的弦P3P4”,求以此两弦为对 角线的内接四边形的面积的最小值。弄清问题(解题应从弄清问题开始)
①化简策略:从最复杂的地方开刀
②语言变换策略:用不同的语言重新叙述
③分析策略:假设问题已经解决
变换问题
①联想策略:联想一个熟悉的问题
②讨论策略:先解决问题的部分解题策略方法2:语言变换 数形结合。
f(x)=∣x+2∣,g(x)=∣x∣。方法1:讨论 分x≤-2,-2 (x+2)2≥x2 → x≥-1。解不等式∣x+2∣≥∣x∣
思路:化简 去掉绝对值符号。
与解题指要 一、数学高考介绍二、数学知识梳理三、数学试题简析四、数学解题指要 (’99全国)向高为H的水瓶中注水,
注满为止,如果注水量V与水深h的
函数关系的图象如右图所示,那么
水瓶的形状是( )
一、高考数学命题的特点与要求高考数学命题的特点B 位置?数值 h H V V0 O f( )= = f ( x )+f ( )=1.(2002 全国)已知函数f (x)=
则 f( 1 )+f( 2 )+f( )+f( 3 )+f( )+f( 4 )+
f ( )= .结构特征 高考数学是考查数学基础的考试①基础知识
②基本技能
③基本数学思想方法
a、数形结合(转换策略)
b、函数与方程(分析策略)
c、分类讨论(分解策略)
d、等价转换(分析策略)
①在高考数学命题中,经历了“以知识立意”到以“问题立意”,再发展为“以能力立意”的过程。
②以能力立意命题,保障了高考突出能力与学习 潜能考查的要求。
③以能力立意命题拓展了命题思路。
④以能力立意命题于题型设计,易于形成综合自 然、新颖脱俗的试题。
⑤以能力立意命题在全卷的整合时,对试题的整体布局、层次安排有高屋建瓴之势。。
⑥以能力立意命题促进了高考改革的深入发展。高考数学注重能力考查 3+4+6+6=19高考数学对难度和速度均有要求 木 桶 原 理知识要求
①了解
②理解和掌握
③灵活和综合运用
能力要求
①思维能力
②运算能力
③空间想像能力
④实践能力
⑤创新意识
个性品质要求高考数学的要求二、高考数学知识梳理与复习高考数学知识梳理 平面向量 ①理解向量的概念,掌握向量的几何表, 了解共线向量的概念。②掌握向量的加法与减法。 ③掌握实数与向量的积,理解两个向量 共线的充要条件。④了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。
⑤掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件。
⑥掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用、掌握平移公式。①理解集合、子集、补集、交集、并集的 概念。了解空集和全集的意义。了解属 于、包含、相等关系的意义。掌握有关 的术语和符号,并会用它们正确表示一 些简单的集合。
②理解逻辑联结词“或”、“且”、“非” 的含义。理解四种命题及其相互关系,掌 握充分条件、必要条件及充要条件的意 义。集合、简易逻辑函数①了解映射的概念,理解函数的概念。
②了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法。
③了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数。
④理解分数指数幂的概念,掌握有理指数幂的运算性质。掌握指数函数的概念、图象和性质⑤理解对数的概念,掌握对数的运算性质, 掌握对数函数的概念、图像和性质。
⑥能够运用函数的性质、指数函数和对数函 数的性质解决某些简单的实际问题。 ①理解不等式的性质及其证明。
②掌握两个(不扩展到三个)正数的算术 平均数不小于它们的几何平均数的定 理,并会简单的应用。
③掌握分析法、综合法、比较法证明简单 的不等式。
④掌握简单不等式的解法。
⑤理解不等式
∣a∣- ∣ b∣≤∣a+b∣≤∣a∣+∣b∣不等式①理解任意角的概念、弧度的意义,能正 确地进行弧度与角度的换算。
②掌握任意角的正弦、余弦、正切的定 义。了解余切、正割、余割的定义 ,掌 握同角三角函数的基本关系式: sin2α+cos2α=1, ,tanαcotα=1。 掌握正弦、余弦的诱导公式。了解周期 函数与最小正周期的意义。
③掌握两角和与两角差的正弦、余弦、正切 公式。掌握二倍角的正弦、余弦、正切公式。三角函数④能正确运用三角公式,进行简单的三角函 数式的化简、求值和恒等式证明。
⑤了解正弦函数、余弦函数、正切函数的图 像和性质,会用“五点法”画正弦函数、 余弦函数和函数y=Asin(ωx+ψ)的简图, 理解A、ω、ψ的物理意义。
⑥会由已知三角函数值求角,并会用符号 arcsinx、arccosx、arctanx表示。
⑦掌握正弦定理、余弦定理,并能初步运用 它们解斜三角形。①理解数列的概念,了解数列通项公式的 意义,了解递推公式是给出数列的一种 方法,并能根据递推公式写出数列的前 几项。
②理解等差数列的概念,掌握等差数列的 通项公式与前n项和公式,并能解决简单 的实际问题。
③理解等比数列的概念,掌握等比数列的 通项公式与前n项和公式,并能解决简单 的实际问题。数列①理解直线的倾斜角和斜率的概念,掌握过 两点的直线的斜率公式。掌握直线方程的 点斜式、两点式、一般式,并能根据条件 熟练地求出直线方程。
②掌握两条直线平行与垂直的条件,两条直 线所成的角和点到直线的距离公式。能够 根据直线的方程判断两条直线的位置关 系。
③了解二元一次不等式表示平面区域。直线和圆的方程④了解线性规划的意义,并会简单的应用。
⑤了解解析几何的基本思想,了解坐标法。
⑥掌握圆的标准方程和一般方程,理解圆的 参数方程。①掌握椭圆的定义、标准方程和椭圆的简 单几何性质。理解椭圆的参数方程。
②掌握双曲线的定义、标准方程和双曲线
的简单几何性质。
③掌握抛物线的定义、标准方程和抛物线 的简单几何性质。
④了解圆锥曲线的初步应用。圆锥曲线方程①掌握平面的基本性质,会作斜二测的画 法画水平放置的平面图形的直观图;能 够画出空间两条直线、直线和平面的各 种益关系的图形,能够根据图形想像它 们的位置关系。
②掌握直线和平面平行的判定定理和性质 定理;掌握直线和平面垂直的判定定 理;掌握三垂线定理及其逆定理。
③理解空间向量的概念,掌握空间向量的 加法、减法和数乘。直线、平面、简单几何体④了解空间向量的基本定理;理解空间向量 坐标的概念,掌握空间向量的坐标运算。
⑤掌握空间向量的数量积的定义及其性质; 掌握用直角坐标计算空间向量数量积的
公式;掌握空间两点间距离公式。
⑥理解直线的方向向量、平面的法向量、向 量在平面内的射影等概念。
⑦掌握直线和直线、直线和平面、平面和平 面所成的角、距离的概念。⑧了解多面体、凸多面体的概念,了解正多 面体的概念。
⑨了解棱柱的概念,掌握棱柱的性质,会画 直棱柱的直观图。
⑩了解棱锥的概念,掌握正棱锥的性质,会 画正棱锥的直观图。
11了解球的概念,掌握球的性质,掌握球的 表面积、体积公式○
①掌握分类计数原理与分步计数原理,并 能用它们分析和解决一些简单的应用问 题。
②理解排列的意义,掌握排列数计算公 式,并能用它解决一些简单的应用问题。
③理解组合的意义,掌握组合数计算公式和 组合数的性质,并能用它们解决一些简单 的应用问题。
④掌握二项式定理和二项展开式的性质,并 能用它们计算和证明一些简单的问题。排列、组合、二项式定理①了解随机事件的发生存在着规律性的随 机事件概率的意义。
②了解等可能性事件的概率的意义,会用 排列组合的基本公式计算一些等可能性 事件的概率。
③了解互斥事件与相互独立事件的意义, 会用互斥事件的概率加法公式与相互独 立事件的概率乘法公式计算一些事件的 概率。
④会计算事件在n次独立重复试验中恰好发 生k次概率。概率①了解随机抽样,了解分层抽样的意义, 会用它们对简单实际问题进行抽样。
②会用样本频率分布估计总体分布。
③会用样本估计总体期望值和方差。统计①了解导数概念的实际背景。
②理解导数的几何意义。
③掌握函数y=c(C为常数)、y=xn(n∈N+) 的导数公式,会求多项式函数的导数。
④理解极大值、极小值、最大值、最小值的 概念,并会用导数求多项式函数的单调区 间、极大值、极小值及闭区间上的最大值 和最小值。
⑤会利用导数求某些简单实际问题的最大 值和最小值。 导数设函数f(x)的导数为f ?(x), 且 f(x)=x3+2x f ?(1)
则 f ?(0)= ( ) A. 0 B. -3 C. -6 D. 6 理解 f ?(1)是常量 ∵ f ?(x)=3x2+2f ?(1), ∴ f ?(0)=2f ?(1). ① 又 f ?(1)=3+2f ?(1),∴ f ?(1)=-3.代入 ①式,得 f ?(0)=-6.高考复习“四字诀”②深层次挖掘教材
如:{an}为等差数列,a1、a2、a9成等比数列
则
题目的来源:选择特殊数列为背景,最常 见、最先想到的是自然数列,易知它满足条 件,所以选an=n。
再如函数这一部分,复习时可对y= 和 y=logax的图象和性质进行研究。广:天高任鸟飞 ①全面复习,知识和能力并重
②学会学习新:万变不离其宗
①“旧题”新解,追求优美
例如:过抛物线y2=x上一点(4,2),作倾
角互补的两条直线AB、AC交抛物线 B、C,求证:直线BC的斜率为定值。
思考: 按照与作图步骤相吻合的思路来求解。 解:设KAB=K,则,KAC=-K,AB的方程为 y=k(x-4)+2
因此,A(4,2),B(XB,YB)是方程组
可求得KBC=再思考:在解题过程中,求B点坐标的计算量比较 大,应该想办法改进。我们还再回顾一下原来的解题程序。
设KAB→写直线AB、AC的方程→解出B、C→表示KBC改进:先设B、C坐标。
改进后的程序为:
设B、C坐标→求出KAB、KAC→表示KBC
设B( ,t2),C( ,t2)(∣t1∣≠∣t2∣)
这时KAB= , KAC=
∵KAB=-KAC,即x0ABCy化简得:t1+2= -(t2+2)
下面怎么办?似乎迷失了方向。我们还是应该明确一下本题的目标。要证明KBC是一个定值,于是不妨先求出
KBC KBC=这就好了,原来是要证明t1+t2是定值。
这样,就自然想到将t1+2=-(t2+2)变形为 t1+t2= - 4
本题圆满获得解决。再改进:设B、C坐标→表示KBC→求出KAB、KAC②看透本质,新题通法。 “知识与技能”突出思想和智慧
程序性
主干性
这里的技能特性也有两点:
独立操作性:由重复再现过渡到独立 完成;
迁移性:通过联系的思想与转换的手 段达到灵活运用、举一反三和触类旁 通的目的。三、去年高考数学试题的亮点 例1 (高考第一题第6小题)某校为了了解学生的课外 阅读情况,随机调查了50名学生,得到他们在某 一天各自课外阅读所用时间的数据,结果用图形 表示,根据条形图可得这50名学生这一天平均每 人的课外阅读时间为
A、0.6小时
B、0.9小时
C、1.0小时
D、1.5小时
解析 一天平均每人课外阅读时间为
=0.9(小时)
故选B。时间(小时)
0 0.5 1.0 1.5 2.0 x
y
20
15
10
5
人数(人)
例2(高考第一题第8小题)设k>1,f(x)=k(x-1) (x∈R)。在平面直角坐标系xOy中,函数 y=f(x)的图象与x轴变于A点,它的反函数
y=f-1(x)的图象与y轴交于B点,并且这两个函
数的图象交于P点,已知四边形OAPB的面积是
3,则k等于( )
A、 3
B、
C、
D、0 1 A xy
1
Bp解析:依题意A(1,0),B(0,1), y=f(x)与y=f-1(x)的交点必在 直线y=x上。
由 y=k(x-1),
y=x
解得:x=
因为S四边形OAPB=2S△OPA=2· ∣OA∣·∣xp∣= =3,
所以k= 。
故此选B“过程与方法”重视价值和策略
例3 (高考第二题第16小题)平面向量a、b
中,已知a=(4,-3),∣b∣=1且a·b=5 则向量b= 。 [方法1] 设a与b夹角为θ。
则由a·b=5→∣a∣∣b∣cosθ=5
→5·1·cosθ=5
→cosθ=1
→θ=0o
所以b与a共线且方向相同,
b=( ,- )。解析 解决本题至少可从这样两个角度思考[方法2] 设b=(x,y)
x2+y2=1 x=
4x-3y=5 y= -
或利用直线4x-3y=5与圆x2+y2=1相切的特征,借助几何图形,利用几何方法,求得切点坐标为( ,- )
b=( ,- )则 →“情感、态度与价值观”体现感悟和动力
例4(高考第六大题)制订投资计划时, 不仅要考虑可能获得的盈利,而且要考 虑可能出现的亏损。
某投资人打算投资甲、乙两个项目,根 据预测,甲、乙项目可能的最大利率分别 为100%为50%,可能的最大亏损率分别为 30%和10%,投资人计划投资金额超过10 万元,要求确保可能的资金亏损不超过1.8 万元。问投资人对甲、乙两个项目各投资 多少万元,才能使可能的盈利最大?解析 设投资人分别用x万元,y万元投资甲、乙两个项目,由题意知
x+y≤10,
0.3X+0.1y≤1.8,
x≤0,
y≥0.
目标函数z=x+0.5y.
上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域。
作直线L:x+0.5y=0,并作平行于直线L的一组直线。
X+0.5y=z,z∈R,与可行域相交,其中有一条直线经过可行域上的M点,且与直线x+0.5y=0的距离最大,这里M点是直线x+y=10和0.3x+0.1y=1.8的交点。Y
18
10
0 6 10 x
0.3x+0.1y=1.8
x+0.5y=0M(4,6)
x+y=10L解方程组
x+y=10
0.3x+0.1y=1.8
得x=4,y=6
此时z=1×4+0.5×6=7(万元)
因为7>0,
所以x=4,y=6时z取最大值。
答:投资人用4万元投资甲项目、6万元投 资乙项目,才能在确保亏损不超过1.8 万元的前提下,使可能的盈利最大。多思善想
思联系,网络知识,夯实基础
例1 α、β是两个不同的平面,m、n是 平面α及β之外的两条不同直线,给 出四个论断:①m⊥n,②α⊥β, ③n⊥β,④m⊥α,以其中三个论 断作为条件,余下一个论断作为结 论,写出你认为正确的一个命题 。 四、高考数学复习解题指要思路1:题目结构中a、b、c具有轮换对称性, 可将右式分为三个部分,用综合法易证: (a+b), (b+c), (a+c),三式相加即得。 例2 已知a>0,b>0,c>0,求证:
(a+b+c)
思多解,多方出击,培养思维的发散性是三角函数的特殊值,联系三角知识,可从右边证到左边。
思路2:(a+b)=asin+bcos=sin(+φ)≤(a+c)≤三式相加即得。(b+c)≤ B
α
a
b
A c同理: ≥ (a+c)
三式相加即得。 思路3 观察左边三个根式,联系立几知识,它们 是以a、b、c为三度的长方体的三个面的对 角线长度,可构造长方体来证明,如图:
∣AB∣= ,
a+b=∣AB∣sinα+∣AB∣cosα
= (sinα+cosα)
= sin(α+ )
≤
所以 ≥ (a+b)思规律,找变化,触类旁通例3 试证以过椭圆的焦点的弦为直径的圆必 和椭圆相应的准线相离。
例4 已知异面直线a和b所成的角为50o,P为 空间任一定点,则P点且与a、b所成的角都是30o的直线有且仅有 ( )
A、1条 B、2条 C、3条 D、4条
在本题中50o和30o的设置对答案起着重要作用。因此,可通过改变50o和30o的大小来深化对这类题目的理解。(1)若将50o改为25o,其余条件不变,则答 案是 。
(2)若将50o改为65o,其余条件不变,则答 案 。
(3)若将30o改为70o,其余条件不变,则答 案是 。
(4)若将50o改为xo,30o改为yo,且答案为A, 则x、y的关系式为 ;若答案为B,则 x、y的关系为 ;若答案为C,则x、 y的关系为 ;若答案为D,则x、y的 关系为 。例5 求和S=(x+ )+(x2+ )+…+(xn+ )
错解:
S=(x+x2+x3+…+xn)+( + + …+ )
= +
这是应用等比数列求和公式时很容易出现的 问题,按照等比数列求和公式,当公式q是一个不确 定的数时,求其前n项和,则要考虑q=1,q≠1两种情 况,因此应分四种情形求解:(1)x=1,y≠1; (2)x≠1,y=1;(3)x=1,y=1;(4)x≠1,y≠1思错处,找错因,提高辨别解题错误的能力例6 过抛物线y2=2px(p>0)的焦点的一条直线和 这条抛物线相交于P1、P2两点,两个交点的 纵坐标分别为y1、y2,求证:y1y2=-p2
①已知条件不变时
a、求证:x1x2= ;
b、求焦点弦∣P1P2∣的长;
c、求△OP1P2的面积;
d、求焦点弦P1P2中点的轨迹方程;
e、求证 :
f、求证:以焦点弦为直径的圆必与准线 相切。 思演变,层层深入,提高应变能力②改成逆命题:一条直线与抛物线y2=2px(p>0) 相交于P1(x1,y1)、P2(x2,y2)两点,如果 满足y1y2=-p2(或x1x2= ),那么这条直线过 抛物线的焦点。
③已知条件不变,再附加条件“过P1、P2分别作x 轴的垂线,垂足为M1、M2”,求证: ∣OM1∣、∣OF∣、∣OM2∣成等比数列。
④已知条件不变,再附加条件“过焦点F,再作 一条与P1P2垂直的弦P3P4”,求以此两弦为对 角线的内接四边形的面积的最小值。弄清问题(解题应从弄清问题开始)
①化简策略:从最复杂的地方开刀
②语言变换策略:用不同的语言重新叙述
③分析策略:假设问题已经解决
变换问题
①联想策略:联想一个熟悉的问题
②讨论策略:先解决问题的部分解题策略方法2:语言变换 数形结合。
f(x)=∣x+2∣,g(x)=∣x∣。方法1:讨论 分x≤-2,-2
思路:化简 去掉绝对值符号。
同课章节目录
