计算题专项:三角形(专项训练)-小学数学四年级下册人教版(含解析)
文档属性
| 名称 | 计算题专项:三角形(专项训练)-小学数学四年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 16:33:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
计算题专项:三角形(专项训练)-小学数学四年级下册人教版
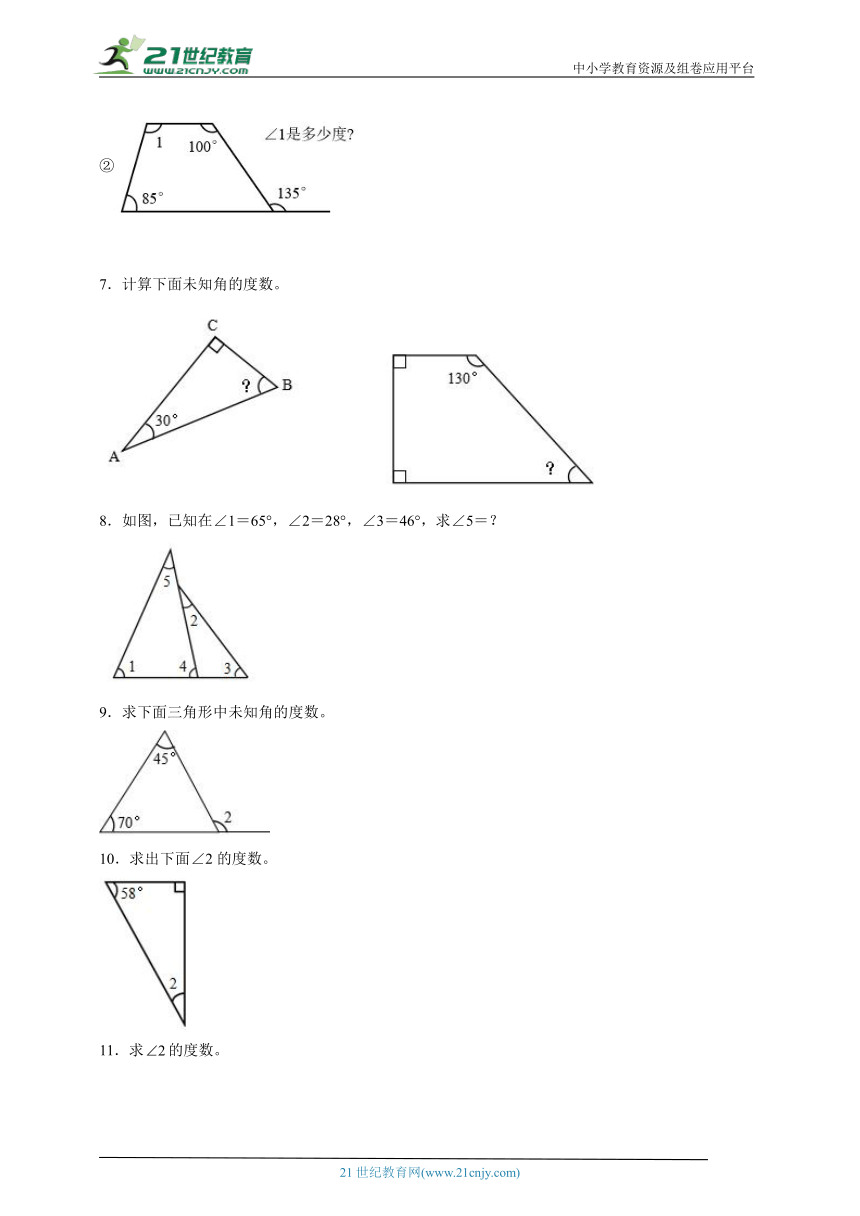
1.下图是等腰三角形,已知∠2=40°,求∠1的度数。
2.已知∠1=105°,求∠2的度数。
3.求出图中未知角的度数。
(1) (2)
4.求出各题中∠1的度数。
5.算出下面各个未知角的度数。
6.算一算角的度数。
①
②
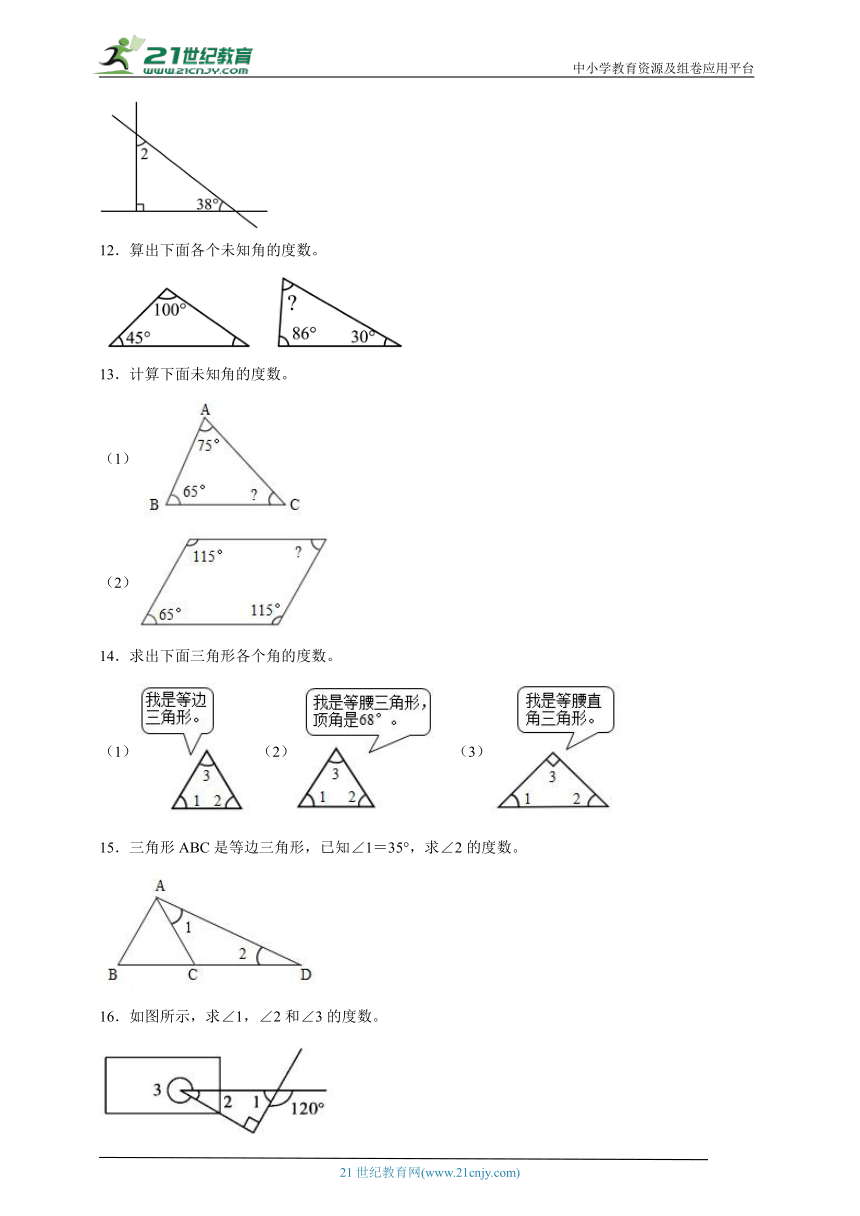
7.计算下面未知角的度数。
8.如图,已知在∠1=65°,∠2=28°,∠3=46°,求∠5=?
9.求下面三角形中未知角的度数。
10.求出下面∠2的度数。
11.求的度数。
12.算出下面各个未知角的度数。
13.计算下面未知角的度数。
(1)
(2)
14.求出下面三角形各个角的度数。
(1) (2) (3)
15.三角形ABC是等边三角形,已知∠1=35°,求∠2的度数。
16.如图所示,求∠1,∠2和∠3的度数。
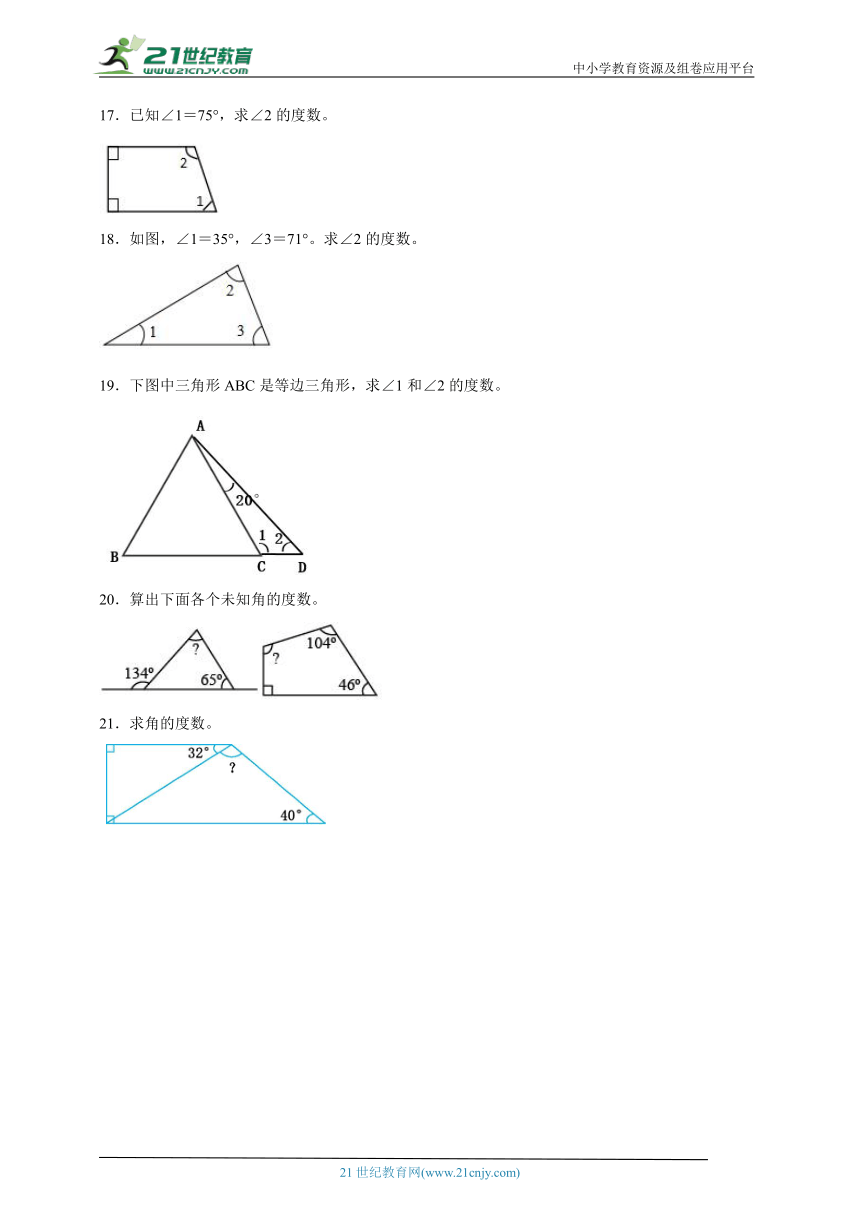
17.已知∠1=75°,求∠2的度数。
18.如图,∠1=35°,∠3=71°。求∠2的度数。
19.下图中三角形ABC是等边三角形,求∠1和∠2的度数。
20.算出下面各个未知角的度数。
21.求角的度数。
参考答案:
1.∠1=100°
【分析】一个等腰三角形的两个底角相等,三角形的内角和是180°,用180°减去2个40°就是顶角的度数,即∠1的度数。
【详解】∠1=180°-40°×2
=180°-80°
=100°
2.∠2=105°
【分析】根据平角=180°,已知∠1的度数,利用减法即可求出与梯形中锐角的度数,再根据四边形内角和为360°,用360°减去两个直角和一个锐角的度数即可求出∠2的度数。
【详解】180°-105°=75°
360°-90°-90°-75°
=270°-90°-75°
=180°-75°
=105°
所以∠2=105°。
3.(1)
(2)
【分析】(1)如图一个直角三角形,那么一个角是90度,另两个角的和是90度,用90度减去给出的一个角的度数就是所求的角的度数;
(2)根据三角形内角和度数是180度,减去所给的两个角的度数,就是所求角的度数,据此解答。
【详解】(1)
(2)
4.57°;63°
【分析】(1)观察图形可知,三角形的第三个内角与115°组成平角,平角=180°,据此利用180°减去115°,先求出三角形的第三个内角的度数;再根据三角形的内角和是180°,用180°减去两个已知角的度数就等于∠1的度数;
(2)根据四边形的内角和是360°,用360°减去三个已知角的度数就等于∠1的度数。
【详解】180°-58°-(180°-115°)
=180°-58°-65°
=122°-65°
=57°
360°-117°-63°-117°
=243°-63°-117°
=180°-117°
=63°
5.36°;22°
【分析】等腰三角形的两腰相等,两个底角也相等;三角形的内角和为180°,因此用180°减去另外两个角的度数之和即可;1直角=90°,依此计算。
【详解】图一:72°+72°=144°
180°-144°=36°
图二:90°+68°=158°
180°-158°=22°
6.①∠1=50°;②∠1=130°
【分析】①如下图,∠2等于180°减140°, 180°减90°,再减∠2等于∠1;
②如下图,∠2等于180°减135°,四边形内角和等于360°,360°减100°,再减85°,然后减∠2等于∠1。
【详解】①∠2=180°-140°=40°
∠1=180°-90°-∠2
=90°-40°
=50°
②∠2=180°-135°=45°
∠1=360°-100°-85°-∠2
=175°-45°
=130°
7.60°;50°
【分析】(1)三角形的内角和是180°,直角三角形的两个锐角之和是90°,根据减法的意义,用减法解答;
(2)四边形的内角和是360°,直角梯形有两个直角,根据减法的意义,用360°减去已知的3个内角的度数即可。
【详解】90°-30°=60°
360°-(90°+90°+130°)
=360°-(180°+130°)
=360°-310°
=50°
8.∠5=41°
【分析】三角形的内角和为180°,一个平角也是180°,即180°-(∠2+∠3)=180°-∠4,即∠2+∠3=∠4,因此用180°减去∠2与∠3的度数和之后,再减去∠1的度数即可,依此计算。
【详解】28°+46°=74°
∠5=180°-74°-65°=106°-65°=41°
9.115°
【分析】根据三角形的内角和是180度,用180度减去三角形中已知的两个内角,求出三角形的第三个角,再根据平角是180度,用180度减去三角形的第三个角即可求出∠2的度数。
【详解】180°-70°-45°
=110°-45°
=65°
180°-65°=115°
10.32°
【分析】根据三角形的内角和等于180°,解答此题即可。
【详解】根据图示可知三角形为直角三角形。
∠2=180°-90°-58°
=90°-58°
=32°
11.52°
【分析】三角形的内角和是180°,图中是一个直角三角形,用180°-90°-38°即可求出∠2的度数。
【详解】180°-90°-38°
=90°-38°
=52°
12.35°;64°
【分析】三角形的内角和为180°,因此图一中用180°减去100°后,再减去45°即可;图二用180°减去86°后,再减去30°即可,依此计算。
【详解】图一:
180°-100°=80°
80°-45°=35°
图二:
180°-86°=94°
94°-30°=64°
13.(1)40°;
(2)65°
【分析】(1)三角形的内角和是180°,减去图中已知的75度和65度即可求解;
(2)平行四边形的内角和是360°,减去已知的三个角即可求解未知角;
【详解】(1)180°-75°-65°
=105°-65°
=40°
(2)360°-115°-115°-65°
=245°-115°-65°
=130°-65°
=65°
14.(1)∠1=60°、∠2=60°、∠3=60°;
(2)∠1=56°、∠2=56°、∠3=68°;
(3)∠1=45°、∠2=45°、∠3=90°;
【分析】(1)等边三角形:三条边都相等且三个内角均相等,都是60°。
(2)等腰三角形:有两条边相等的三角形,在等腰三角形中,相等的两条边叫做腰,另一条边叫做底;两腰的夹角叫做顶角,底边上的两个角叫做底角;等腰三角形的两个底角相等。
(3)有一个角是直角的三角形是直角三角形。
【详解】(1)180°÷3=60°
则∠1=60°、∠2=60°、∠3=60°。
(2)(180°-68°)÷2
=112°÷2
=56°
则∠1=56°、∠2=56°、∠3=68°。
(3)(180°-90°)÷2
=90°÷2
=45°
则∠1=45°、∠2=45°、∠3=90°。
15.25°
【分析】三角形ABC是等边三角形,可得出∠ACB等于60°,∠ACD等于180°减60°等于120°,∠2等于180°减去∠1和∠ACD,据此即可解答。
【详解】三角形ABC是等边三角形,则∠ACB=60°;
∠ACD=180°-∠ACB
=180°-60°
=120°
∠2=180°-∠1-∠ACD
=180°-35°-120°
=145°-120°
=25°
16.∠1=60°,∠2=30°,∠3=330°
【分析】根据题图可知,∠1和120°的角组成一个平角,则∠1=180°-120°。∠1、∠2和一个直角是三角形的三个内角,根据三角形的内角和为180°可知,∠2=180°-90°-∠1。∠2和∠3组成一个周角,则∠3=360°-∠2。
【详解】∠1=180°-120°=60°
∠2=180°-90°-60°=30°
∠3=360°-30°=330°
17.105°
【分析】四边形的内角和是360°,因此∠2=360°-90°-90°-∠1,依此计算。
【详解】∠2=360°-90°-90°-75°
=270°-90°-75°
=180°-75°
=105°
18.∠2=74°
【分析】因为三角形的内角和是180度,所以用180度减去已知的两个角的度数,即可求出第三个角的度数。
【详解】∠2=180°-71°-35°
=109°-35°
=74°
19.∠1=120°;∠2=40°
【分析】因为三角形ABC为等边三角形,则其三个角的度数都为60°,根据已知条件,由平角的定义即可求出∠1的度数,再根据三角形内角和是180°求出∠2的度数。
【详解】因为三角形ABC是等边三角形,且每个角都等于60°,
所以∠1=180°-60°=120°,
∠2=180°-20°-120°
=160°-120°
=40°
20.69°;120°
【分析】(1)三角形的一个角与一个134°的角组成平角,据此即可求出三角形这个角的度数,然后再根据三角形内角和定理即可求出这个三角形另外一个角的度数。
(2)根据多边形内角和定理可知,四边形的内角和是360°,用内角和度数减掉已知三个角的度数,就是第四个角的度数。
【详解】180°-134°=46°
180°-46°-65°
=134°-65°
=69°
360°-104°-46°-90°
=256°-46°-90°
=210°-90°
=120°
21.108°
【分析】图中梯形是两个三角形组成的,根据三角形内角和可求出梯形的内角和;已知梯形的两个角是直角,一个是40°,还有一个角是32°与未知角的和;用梯形是内角和减去已知角的度数即可解题。
【详解】梯形内角和:180°×2=360°
未知角的度数:360°-90°-90°-40°-32°
=270°-90°-40°-32°
=180°-40°-32°
=140°-32°
=108°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
计算题专项:三角形(专项训练)-小学数学四年级下册人教版
1.下图是等腰三角形,已知∠2=40°,求∠1的度数。
2.已知∠1=105°,求∠2的度数。
3.求出图中未知角的度数。
(1) (2)
4.求出各题中∠1的度数。
5.算出下面各个未知角的度数。
6.算一算角的度数。
①
②
7.计算下面未知角的度数。
8.如图,已知在∠1=65°,∠2=28°,∠3=46°,求∠5=?
9.求下面三角形中未知角的度数。
10.求出下面∠2的度数。
11.求的度数。
12.算出下面各个未知角的度数。
13.计算下面未知角的度数。
(1)
(2)
14.求出下面三角形各个角的度数。
(1) (2) (3)
15.三角形ABC是等边三角形,已知∠1=35°,求∠2的度数。
16.如图所示,求∠1,∠2和∠3的度数。
17.已知∠1=75°,求∠2的度数。
18.如图,∠1=35°,∠3=71°。求∠2的度数。
19.下图中三角形ABC是等边三角形,求∠1和∠2的度数。
20.算出下面各个未知角的度数。
21.求角的度数。
参考答案:
1.∠1=100°
【分析】一个等腰三角形的两个底角相等,三角形的内角和是180°,用180°减去2个40°就是顶角的度数,即∠1的度数。
【详解】∠1=180°-40°×2
=180°-80°
=100°
2.∠2=105°
【分析】根据平角=180°,已知∠1的度数,利用减法即可求出与梯形中锐角的度数,再根据四边形内角和为360°,用360°减去两个直角和一个锐角的度数即可求出∠2的度数。
【详解】180°-105°=75°
360°-90°-90°-75°
=270°-90°-75°
=180°-75°
=105°
所以∠2=105°。
3.(1)
(2)
【分析】(1)如图一个直角三角形,那么一个角是90度,另两个角的和是90度,用90度减去给出的一个角的度数就是所求的角的度数;
(2)根据三角形内角和度数是180度,减去所给的两个角的度数,就是所求角的度数,据此解答。
【详解】(1)
(2)
4.57°;63°
【分析】(1)观察图形可知,三角形的第三个内角与115°组成平角,平角=180°,据此利用180°减去115°,先求出三角形的第三个内角的度数;再根据三角形的内角和是180°,用180°减去两个已知角的度数就等于∠1的度数;
(2)根据四边形的内角和是360°,用360°减去三个已知角的度数就等于∠1的度数。
【详解】180°-58°-(180°-115°)
=180°-58°-65°
=122°-65°
=57°
360°-117°-63°-117°
=243°-63°-117°
=180°-117°
=63°
5.36°;22°
【分析】等腰三角形的两腰相等,两个底角也相等;三角形的内角和为180°,因此用180°减去另外两个角的度数之和即可;1直角=90°,依此计算。
【详解】图一:72°+72°=144°
180°-144°=36°
图二:90°+68°=158°
180°-158°=22°
6.①∠1=50°;②∠1=130°
【分析】①如下图,∠2等于180°减140°, 180°减90°,再减∠2等于∠1;
②如下图,∠2等于180°减135°,四边形内角和等于360°,360°减100°,再减85°,然后减∠2等于∠1。
【详解】①∠2=180°-140°=40°
∠1=180°-90°-∠2
=90°-40°
=50°
②∠2=180°-135°=45°
∠1=360°-100°-85°-∠2
=175°-45°
=130°
7.60°;50°
【分析】(1)三角形的内角和是180°,直角三角形的两个锐角之和是90°,根据减法的意义,用减法解答;
(2)四边形的内角和是360°,直角梯形有两个直角,根据减法的意义,用360°减去已知的3个内角的度数即可。
【详解】90°-30°=60°
360°-(90°+90°+130°)
=360°-(180°+130°)
=360°-310°
=50°
8.∠5=41°
【分析】三角形的内角和为180°,一个平角也是180°,即180°-(∠2+∠3)=180°-∠4,即∠2+∠3=∠4,因此用180°减去∠2与∠3的度数和之后,再减去∠1的度数即可,依此计算。
【详解】28°+46°=74°
∠5=180°-74°-65°=106°-65°=41°
9.115°
【分析】根据三角形的内角和是180度,用180度减去三角形中已知的两个内角,求出三角形的第三个角,再根据平角是180度,用180度减去三角形的第三个角即可求出∠2的度数。
【详解】180°-70°-45°
=110°-45°
=65°
180°-65°=115°
10.32°
【分析】根据三角形的内角和等于180°,解答此题即可。
【详解】根据图示可知三角形为直角三角形。
∠2=180°-90°-58°
=90°-58°
=32°
11.52°
【分析】三角形的内角和是180°,图中是一个直角三角形,用180°-90°-38°即可求出∠2的度数。
【详解】180°-90°-38°
=90°-38°
=52°
12.35°;64°
【分析】三角形的内角和为180°,因此图一中用180°减去100°后,再减去45°即可;图二用180°减去86°后,再减去30°即可,依此计算。
【详解】图一:
180°-100°=80°
80°-45°=35°
图二:
180°-86°=94°
94°-30°=64°
13.(1)40°;
(2)65°
【分析】(1)三角形的内角和是180°,减去图中已知的75度和65度即可求解;
(2)平行四边形的内角和是360°,减去已知的三个角即可求解未知角;
【详解】(1)180°-75°-65°
=105°-65°
=40°
(2)360°-115°-115°-65°
=245°-115°-65°
=130°-65°
=65°
14.(1)∠1=60°、∠2=60°、∠3=60°;
(2)∠1=56°、∠2=56°、∠3=68°;
(3)∠1=45°、∠2=45°、∠3=90°;
【分析】(1)等边三角形:三条边都相等且三个内角均相等,都是60°。
(2)等腰三角形:有两条边相等的三角形,在等腰三角形中,相等的两条边叫做腰,另一条边叫做底;两腰的夹角叫做顶角,底边上的两个角叫做底角;等腰三角形的两个底角相等。
(3)有一个角是直角的三角形是直角三角形。
【详解】(1)180°÷3=60°
则∠1=60°、∠2=60°、∠3=60°。
(2)(180°-68°)÷2
=112°÷2
=56°
则∠1=56°、∠2=56°、∠3=68°。
(3)(180°-90°)÷2
=90°÷2
=45°
则∠1=45°、∠2=45°、∠3=90°。
15.25°
【分析】三角形ABC是等边三角形,可得出∠ACB等于60°,∠ACD等于180°减60°等于120°,∠2等于180°减去∠1和∠ACD,据此即可解答。
【详解】三角形ABC是等边三角形,则∠ACB=60°;
∠ACD=180°-∠ACB
=180°-60°
=120°
∠2=180°-∠1-∠ACD
=180°-35°-120°
=145°-120°
=25°
16.∠1=60°,∠2=30°,∠3=330°
【分析】根据题图可知,∠1和120°的角组成一个平角,则∠1=180°-120°。∠1、∠2和一个直角是三角形的三个内角,根据三角形的内角和为180°可知,∠2=180°-90°-∠1。∠2和∠3组成一个周角,则∠3=360°-∠2。
【详解】∠1=180°-120°=60°
∠2=180°-90°-60°=30°
∠3=360°-30°=330°
17.105°
【分析】四边形的内角和是360°,因此∠2=360°-90°-90°-∠1,依此计算。
【详解】∠2=360°-90°-90°-75°
=270°-90°-75°
=180°-75°
=105°
18.∠2=74°
【分析】因为三角形的内角和是180度,所以用180度减去已知的两个角的度数,即可求出第三个角的度数。
【详解】∠2=180°-71°-35°
=109°-35°
=74°
19.∠1=120°;∠2=40°
【分析】因为三角形ABC为等边三角形,则其三个角的度数都为60°,根据已知条件,由平角的定义即可求出∠1的度数,再根据三角形内角和是180°求出∠2的度数。
【详解】因为三角形ABC是等边三角形,且每个角都等于60°,
所以∠1=180°-60°=120°,
∠2=180°-20°-120°
=160°-120°
=40°
20.69°;120°
【分析】(1)三角形的一个角与一个134°的角组成平角,据此即可求出三角形这个角的度数,然后再根据三角形内角和定理即可求出这个三角形另外一个角的度数。
(2)根据多边形内角和定理可知,四边形的内角和是360°,用内角和度数减掉已知三个角的度数,就是第四个角的度数。
【详解】180°-134°=46°
180°-46°-65°
=134°-65°
=69°
360°-104°-46°-90°
=256°-46°-90°
=210°-90°
=120°
21.108°
【分析】图中梯形是两个三角形组成的,根据三角形内角和可求出梯形的内角和;已知梯形的两个角是直角,一个是40°,还有一个角是32°与未知角的和;用梯形是内角和减去已知角的度数即可解题。
【详解】梯形内角和:180°×2=360°
未知角的度数:360°-90°-90°-40°-32°
=270°-90°-40°-32°
=180°-40°-32°
=140°-32°
=108°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
