专题五 一次函数与一元一次方程(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
专题五 一次函数与一元一次方程
【知识清单】
1. 一次函数y=kx+b(k,b 为常数,且k ≠ 0)与一元一次方程kx+b=0(k,b 为常数,且k ≠ 0)的关系
数:函数y=kx+b 中,函数值y=0 时自变量x 的值是方程kx+b=0 的解.
形:函数y=kx+b 的图象与x 轴交点的横坐标是方程kx+b=0 的解.
2. 一次函数图象法解一元一次方程的步骤
(1)转化:将一元一次方程转化为一次函数;
(2)画图象:画出一次函数的图象;
(3)找交点:找出一次函数图象与x 轴的交点,交点的横坐标即为一元一次方程的解.
【典型例题】
1.(原创题)已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(1)一次函数的解析式为____________;
(2)关于x的方程kx+b=0的解为________;
关于x的方程kx+b=3的解为________;
关于x的方程kx+b=4的解为________;
(3)直线y=kx+b-3与x轴交点的坐标为______
(4)求该函数图象与两坐标轴围成的三角形的面积.
解答:
(1) y=-x+4
(2) x=8,x=2,x=0
(3)(2,0)
(4)解:由(2)得一次函数y=kx+b的图象与x轴的交点A的坐标为(8,0),所以OA=8.
又易知OB=4,所以该函数图象与两坐标轴围成的三角形的面积=·OB·OA=×4×8=16.
【提升练习】
A级
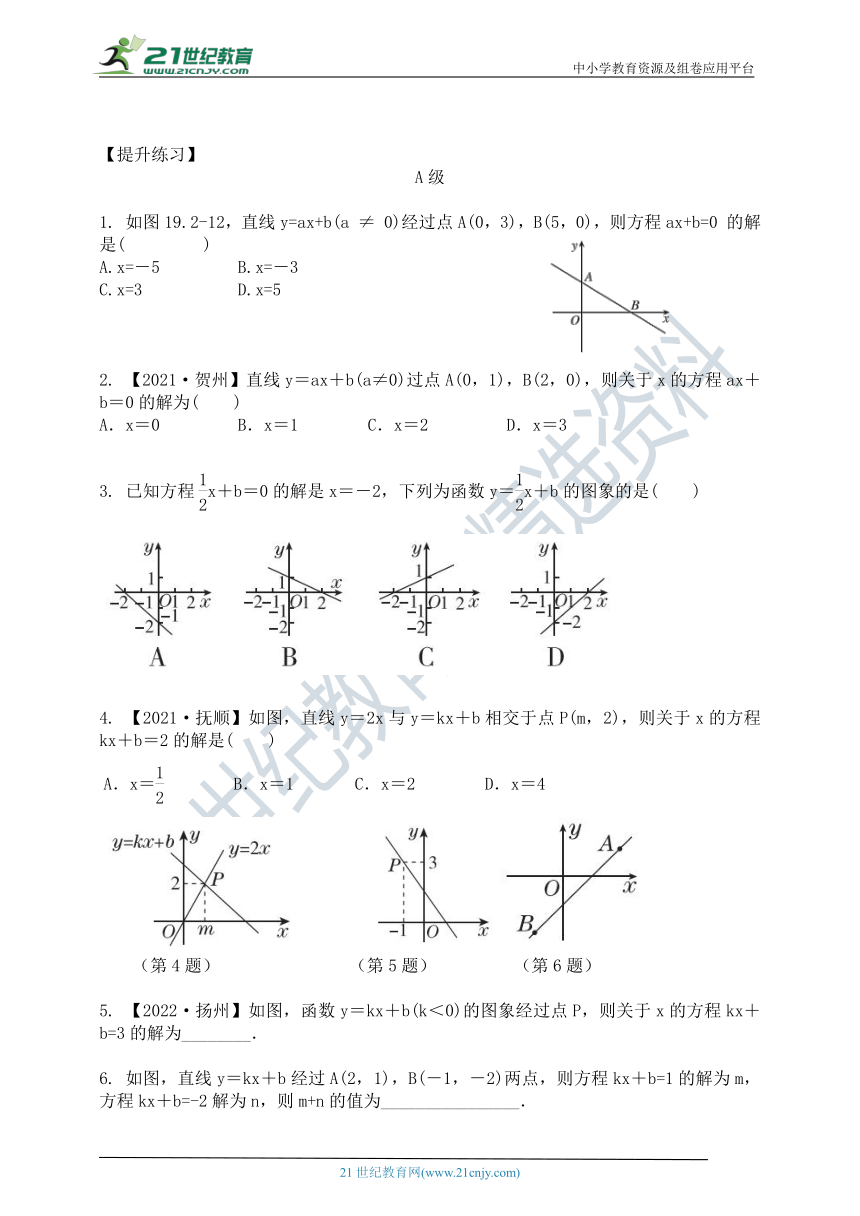
1. 如图19.2-12,直线y=ax+b(a ≠ 0)经过点A(0,3),B(5,0),则方程ax+b=0 的解是( )
A.x=-5 B.x=-3
C.x=3 D.x=5
2. 【2021·贺州】直线y=ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程ax+b=0的解为( )
A.x=0 B.x=1 C.x=2 D.x=3
3. 已知方程x+b=0的解是x=-2,下列为函数y=x+b的图象的是( )
4. 【2021·抚顺】如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
(第4题) (第5题) (第6题)
5. 【2022·扬州】如图,函数y=kx+b(k<0)的图象经过点P,则关于x的方程kx+b=3的解为________.
6. 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则方程kx+b=1的解为m,方程kx+b=-2解为n,则m+n的值为________________.
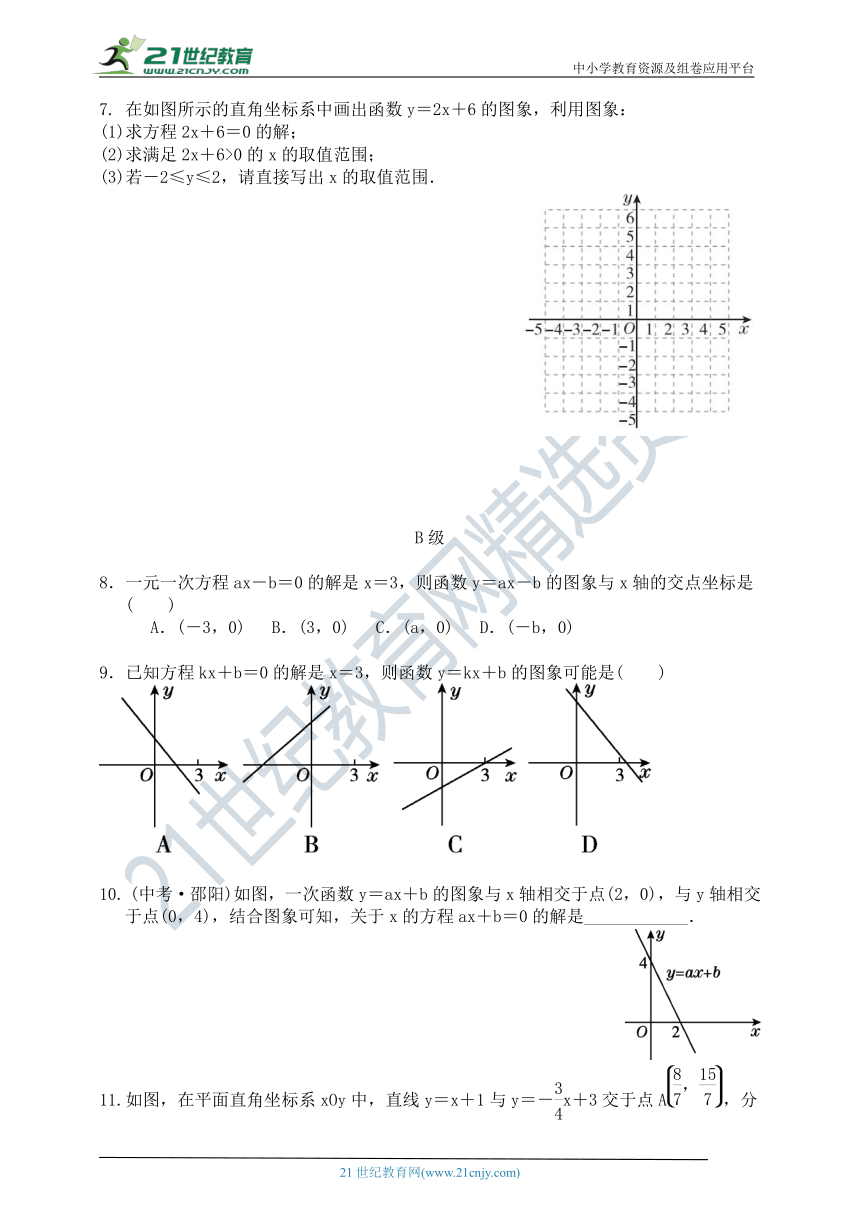
7. 在如图所示的直角坐标系中画出函数y=2x+6的图象,利用图象:
(1)求方程2x+6=0的解;
(2)求满足2x+6>0的x的取值范围;
(3)若-2≤y≤2,请直接写出x的取值范围.
B级
8.一元一次方程ax-b=0的解是x=3,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-3,0) B.(3,0) C.(a,0) D.(-b,0)
9.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是( )
10. (中考·邵阳)如图,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是____________.
11.如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C.
(1)求点B,C的坐标;
(2)求△ABC的面积.
C级
12. (2020·新疆)某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
答案:
A级
1.D 2.C
3. C 4.B
5. x=-1
6. 1
7. 解:(1)图象如图所示.
观察图象知,该函数图象经过点(-3,0),
故方程2x+6=0的解为x=-3.
(2) 解:观察图象知,当x>-3时,y>0,故满足2x+6>0的x的取值范围为x>-3.
(3) 解:当-2≤y≤2时,x的取值范围为-4≤x≤-2.
B级
8.B 9. C
10.x=2
11.解:(1)当y=0时,由x+1=0,解得x=-1,
所以点B的坐标是(-1,0).
当y=0时,由-x+3=0,解得x=4,
所以点C的坐标是(4,0).
(2)解:因为BC=4-(-1)=5,点A到x轴的距离为,
所以S△ABC=×5×=.
C级
12. 解:(1)设A款保温杯的销售单价是a元,则B款保温杯的销售单价是(a+10)元,
=,解得a=30,
经检验,a=30是原分式方程的解且符合题意,则a+10=40.
答:A,B两款保温杯的销售单价分别是30元、40元.
(2) 解:设购买A款保温杯x个,销售利润为w元,则购买B款保温杯(120-x)个,
∴w=(30-20)x+[40×(1-10%)-20](120-x)=-6x+1 920.
∵A款保温杯的数量不少于B款保温杯数量的两倍,
∴x≥2(120-x),解得x≥80.
∵w随x的增大而减小,
∴当x=80时,w取得最大值,此时w=1 440,120-x=40.
答:当购买A款保温杯80个,B款保温杯40个时,才能使这批保温杯的销售利润最大,最大利润是1 440元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题五 一次函数与一元一次方程
【知识清单】
1. 一次函数y=kx+b(k,b 为常数,且k ≠ 0)与一元一次方程kx+b=0(k,b 为常数,且k ≠ 0)的关系
数:函数y=kx+b 中,函数值y=0 时自变量x 的值是方程kx+b=0 的解.
形:函数y=kx+b 的图象与x 轴交点的横坐标是方程kx+b=0 的解.
2. 一次函数图象法解一元一次方程的步骤
(1)转化:将一元一次方程转化为一次函数;
(2)画图象:画出一次函数的图象;
(3)找交点:找出一次函数图象与x 轴的交点,交点的横坐标即为一元一次方程的解.
【典型例题】
1.(原创题)已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(1)一次函数的解析式为____________;
(2)关于x的方程kx+b=0的解为________;
关于x的方程kx+b=3的解为________;
关于x的方程kx+b=4的解为________;
(3)直线y=kx+b-3与x轴交点的坐标为______
(4)求该函数图象与两坐标轴围成的三角形的面积.
解答:
(1) y=-x+4
(2) x=8,x=2,x=0
(3)(2,0)
(4)解:由(2)得一次函数y=kx+b的图象与x轴的交点A的坐标为(8,0),所以OA=8.
又易知OB=4,所以该函数图象与两坐标轴围成的三角形的面积=·OB·OA=×4×8=16.
【提升练习】
A级
1. 如图19.2-12,直线y=ax+b(a ≠ 0)经过点A(0,3),B(5,0),则方程ax+b=0 的解是( )
A.x=-5 B.x=-3
C.x=3 D.x=5
2. 【2021·贺州】直线y=ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程ax+b=0的解为( )
A.x=0 B.x=1 C.x=2 D.x=3
3. 已知方程x+b=0的解是x=-2,下列为函数y=x+b的图象的是( )
4. 【2021·抚顺】如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
(第4题) (第5题) (第6题)
5. 【2022·扬州】如图,函数y=kx+b(k<0)的图象经过点P,则关于x的方程kx+b=3的解为________.
6. 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则方程kx+b=1的解为m,方程kx+b=-2解为n,则m+n的值为________________.
7. 在如图所示的直角坐标系中画出函数y=2x+6的图象,利用图象:
(1)求方程2x+6=0的解;
(2)求满足2x+6>0的x的取值范围;
(3)若-2≤y≤2,请直接写出x的取值范围.
B级
8.一元一次方程ax-b=0的解是x=3,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-3,0) B.(3,0) C.(a,0) D.(-b,0)
9.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是( )
10. (中考·邵阳)如图,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是____________.
11.如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C.
(1)求点B,C的坐标;
(2)求△ABC的面积.
C级
12. (2020·新疆)某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
答案:
A级
1.D 2.C
3. C 4.B
5. x=-1
6. 1
7. 解:(1)图象如图所示.
观察图象知,该函数图象经过点(-3,0),
故方程2x+6=0的解为x=-3.
(2) 解:观察图象知,当x>-3时,y>0,故满足2x+6>0的x的取值范围为x>-3.
(3) 解:当-2≤y≤2时,x的取值范围为-4≤x≤-2.
B级
8.B 9. C
10.x=2
11.解:(1)当y=0时,由x+1=0,解得x=-1,
所以点B的坐标是(-1,0).
当y=0时,由-x+3=0,解得x=4,
所以点C的坐标是(4,0).
(2)解:因为BC=4-(-1)=5,点A到x轴的距离为,
所以S△ABC=×5×=.
C级
12. 解:(1)设A款保温杯的销售单价是a元,则B款保温杯的销售单价是(a+10)元,
=,解得a=30,
经检验,a=30是原分式方程的解且符合题意,则a+10=40.
答:A,B两款保温杯的销售单价分别是30元、40元.
(2) 解:设购买A款保温杯x个,销售利润为w元,则购买B款保温杯(120-x)个,
∴w=(30-20)x+[40×(1-10%)-20](120-x)=-6x+1 920.
∵A款保温杯的数量不少于B款保温杯数量的两倍,
∴x≥2(120-x),解得x≥80.
∵w随x的增大而减小,
∴当x=80时,w取得最大值,此时w=1 440,120-x=40.
答:当购买A款保温杯80个,B款保温杯40个时,才能使这批保温杯的销售利润最大,最大利润是1 440元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
