专题六 一次函数与一元一次不等式(组)(含答案)
文档属性
| 名称 | 专题六 一次函数与一元一次不等式(组)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-14 22:02:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题六 一次函数与一元一次不等式(组)
【知识清单】
1. 一次函数y=kx+b(k,b 为常数,且k ≠ 0)与一元一次不等式kx+b>0(或kx+b<0)(k,b 为常数,且k ≠ 0)的关系
数:函数y=kx+b 中,函数值y>0 时自变量x 的取值范围是不等式kx+b>0 的解集;函数值y<0 时自变量x 的取值范围是不等式kx+b<0 的解集.
形:函数y=kx+b 的图象中,位于x 轴上方的部分对应的自变量x 的取值范围是不等式kx+b>0 的解集;位于x 轴下方的部分对应的自变量x的取值范围是不等式kx+b<0 的解集.
【典型例题】
1.(原创题)如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=-x-2与坐标轴交于B、D两点,两线的交点为P点.
(1)求P点的坐标;
(2)求△APB的面积;
(3)利用图象求当x取何值时,y1>y2.
(4)利用图象直接写出当x取何值时,y1<y2<0.
答案:
解:(1)当y1=y2时,有2x+1=-x-2,
解得x=-1,
∴y=-1.∴P(-1,-1).
(2)令x=0,得y1=1,y2=-2,
∴A(0,1),B(0,-2).∴AB=3.
∴S△APB=×1×3=.
(3)由图象可知:当y1>y2时,x的取值范围是x>-1.
(4) -2<x<-1
【提升练习】
A级
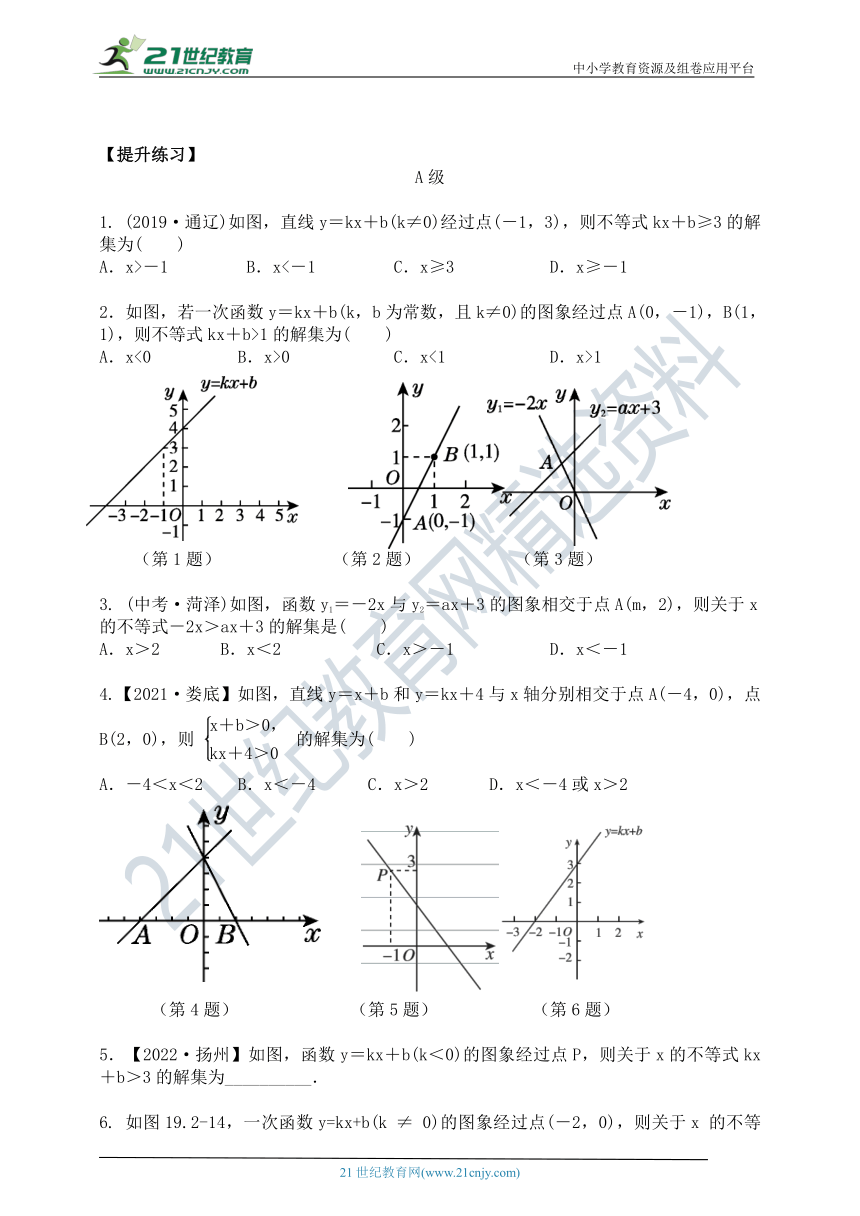
1. (2019·通辽)如图,直线y=kx+b(k≠0)经过点(-1,3),则不等式kx+b≥3的解集为( )
A.x>-1 B.x<-1 C.x≥3 D.x≥-1
2.如图,若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.x<0 B.x>0 C.x<1 D.x>1
(第1题) (第2题) (第3题)
3. (中考·菏泽)如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
A.x>2 B.x<2 C.x>-1 D.x<-1
4.【2021·娄底】如图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),点B(2,0),则 的解集为( )
A.-4<x<2 B.x<-4 C.x>2 D.x<-4或x>2
(第4题) (第5题) (第6题)
5.【2022·扬州】如图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为__________.
6. 如图19.2-14,一次函数y=kx+b(k ≠ 0)的图象经过点(-2,0),则关于x 的不等式k(x-3)+b>0 的解集为 ______.
7.【2022·北京】在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(4,3),(-2,0),且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当x>0时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.
B级
8. 观察图中的函数图象,则关于x的不等式ax-bx>c的解集为( )
A.x<2 B.x<1 C.x>2 D.x>1
(第8题) (第10题)
9.【2021·嘉兴】已知点P(a,b)在直线y=-3x-4上,且2a-5b≤0,则下列不等式一定成立的是( )
A.≤ B.≥ C.≥ D.≤
10. (2020·遵义)如图,直线y=kx+b(k,b是常数k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为____________.
11. (2019·南京)已知一次函数y1=kx+2(k为常数,k≠0)和y2=x-3.
(1)当k=-2时,若y1>y2,求x的取值范围;
(2)当x<1时,y1>y2,结合图象,直接写出k的取值范围.
C级
12. 【2022·广安】某企业下属A,B两厂向甲、乙两地运送水泥共520吨,A厂比B厂少运送20吨,从A厂运往甲、乙两地的运费分别为40元/吨和35元/吨,从B厂运往甲、乙两地的运费分别为28元/吨和25元/吨.
(1)求A,B两厂各运送多少吨水泥;
(2)现甲地需要水泥240吨,乙地需要水泥280吨,受条件限制,B厂运往甲地的水泥最多为150吨,设从A厂运往甲地a吨水泥,A,B两厂运往甲、乙两地的总运费为w元,求w与a之间的函数关系式;请你为该企业设计一种总运费最低的运输方案,并说明理由.
答案:
A级
1.D 2.D 3. D 4.A
5. x<-1
6. x>1
7. 解: (1)把点(4,3),(-2,0)的坐标分别代入y=kx+b,
得解得
∴该函数的解析式为y=x+1.
∵当x=0时,y=×0+1=1,
∴点A的坐标为(0,1).
(2) n≥1.
B级
8.D
9. D
解:∵点P(a,b)在直线y=-3x-4上,
∴-3a-4=b.
又∵2a-5b≤0,
∴2a-5(-3a-4)≤0,
解得a≤-<0.
当a=-时,得b=-,
∴b≥-.
∵2a-5b≤0,
∴2a≤5b.
∴≤.
10.x<4
11.解:(1)解:当k=-2时,y1=-2x+2,
根据题意得-2x+2>x-3,解得x<.
(2)-4≤k≤1且k≠0.
C级
12.解:
(1)设A厂运送x吨水泥,则B厂运送(x+20)吨水泥.
根据题意,得x+x+20=520,
解得x=250.
此时x+20=270.
答:A厂运送250吨水泥,B厂运送270吨水泥.
(2)根据题意,得
w=40a+35(250-a)+28(240-a)+25(a+30)
=40a+8 750-35a+6 720-28a+25a+750
=2a+16 220.
∵B厂运往甲地的水泥最多为150吨,
∴240-a≤150,
解得a≥90.
∵2>0,
∴w随a的增大而增大.
∴当a=90时,总运费最低.
∴250-a=160,240-a=150,a+30=120.
∴总运费最低的运输方案为:
A厂运往甲地90吨水泥,运往乙地160吨水泥;
B厂运往甲地150吨水泥,运往乙地120吨水泥.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题六 一次函数与一元一次不等式(组)
【知识清单】
1. 一次函数y=kx+b(k,b 为常数,且k ≠ 0)与一元一次不等式kx+b>0(或kx+b<0)(k,b 为常数,且k ≠ 0)的关系
数:函数y=kx+b 中,函数值y>0 时自变量x 的取值范围是不等式kx+b>0 的解集;函数值y<0 时自变量x 的取值范围是不等式kx+b<0 的解集.
形:函数y=kx+b 的图象中,位于x 轴上方的部分对应的自变量x 的取值范围是不等式kx+b>0 的解集;位于x 轴下方的部分对应的自变量x的取值范围是不等式kx+b<0 的解集.
【典型例题】
1.(原创题)如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=-x-2与坐标轴交于B、D两点,两线的交点为P点.
(1)求P点的坐标;
(2)求△APB的面积;
(3)利用图象求当x取何值时,y1>y2.
(4)利用图象直接写出当x取何值时,y1<y2<0.
答案:
解:(1)当y1=y2时,有2x+1=-x-2,
解得x=-1,
∴y=-1.∴P(-1,-1).
(2)令x=0,得y1=1,y2=-2,
∴A(0,1),B(0,-2).∴AB=3.
∴S△APB=×1×3=.
(3)由图象可知:当y1>y2时,x的取值范围是x>-1.
(4) -2<x<-1
【提升练习】
A级
1. (2019·通辽)如图,直线y=kx+b(k≠0)经过点(-1,3),则不等式kx+b≥3的解集为( )
A.x>-1 B.x<-1 C.x≥3 D.x≥-1
2.如图,若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.x<0 B.x>0 C.x<1 D.x>1
(第1题) (第2题) (第3题)
3. (中考·菏泽)如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
A.x>2 B.x<2 C.x>-1 D.x<-1
4.【2021·娄底】如图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),点B(2,0),则 的解集为( )
A.-4<x<2 B.x<-4 C.x>2 D.x<-4或x>2
(第4题) (第5题) (第6题)
5.【2022·扬州】如图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为__________.
6. 如图19.2-14,一次函数y=kx+b(k ≠ 0)的图象经过点(-2,0),则关于x 的不等式k(x-3)+b>0 的解集为 ______.
7.【2022·北京】在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(4,3),(-2,0),且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当x>0时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.
B级
8. 观察图中的函数图象,则关于x的不等式ax-bx>c的解集为( )
A.x<2 B.x<1 C.x>2 D.x>1
(第8题) (第10题)
9.【2021·嘉兴】已知点P(a,b)在直线y=-3x-4上,且2a-5b≤0,则下列不等式一定成立的是( )
A.≤ B.≥ C.≥ D.≤
10. (2020·遵义)如图,直线y=kx+b(k,b是常数k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为____________.
11. (2019·南京)已知一次函数y1=kx+2(k为常数,k≠0)和y2=x-3.
(1)当k=-2时,若y1>y2,求x的取值范围;
(2)当x<1时,y1>y2,结合图象,直接写出k的取值范围.
C级
12. 【2022·广安】某企业下属A,B两厂向甲、乙两地运送水泥共520吨,A厂比B厂少运送20吨,从A厂运往甲、乙两地的运费分别为40元/吨和35元/吨,从B厂运往甲、乙两地的运费分别为28元/吨和25元/吨.
(1)求A,B两厂各运送多少吨水泥;
(2)现甲地需要水泥240吨,乙地需要水泥280吨,受条件限制,B厂运往甲地的水泥最多为150吨,设从A厂运往甲地a吨水泥,A,B两厂运往甲、乙两地的总运费为w元,求w与a之间的函数关系式;请你为该企业设计一种总运费最低的运输方案,并说明理由.
答案:
A级
1.D 2.D 3. D 4.A
5. x<-1
6. x>1
7. 解: (1)把点(4,3),(-2,0)的坐标分别代入y=kx+b,
得解得
∴该函数的解析式为y=x+1.
∵当x=0时,y=×0+1=1,
∴点A的坐标为(0,1).
(2) n≥1.
B级
8.D
9. D
解:∵点P(a,b)在直线y=-3x-4上,
∴-3a-4=b.
又∵2a-5b≤0,
∴2a-5(-3a-4)≤0,
解得a≤-<0.
当a=-时,得b=-,
∴b≥-.
∵2a-5b≤0,
∴2a≤5b.
∴≤.
10.x<4
11.解:(1)解:当k=-2时,y1=-2x+2,
根据题意得-2x+2>x-3,解得x<.
(2)-4≤k≤1且k≠0.
C级
12.解:
(1)设A厂运送x吨水泥,则B厂运送(x+20)吨水泥.
根据题意,得x+x+20=520,
解得x=250.
此时x+20=270.
答:A厂运送250吨水泥,B厂运送270吨水泥.
(2)根据题意,得
w=40a+35(250-a)+28(240-a)+25(a+30)
=40a+8 750-35a+6 720-28a+25a+750
=2a+16 220.
∵B厂运往甲地的水泥最多为150吨,
∴240-a≤150,
解得a≥90.
∵2>0,
∴w随a的增大而增大.
∴当a=90时,总运费最低.
∴250-a=160,240-a=150,a+30=120.
∴总运费最低的运输方案为:
A厂运往甲地90吨水泥,运往乙地160吨水泥;
B厂运往甲地150吨水泥,运往乙地120吨水泥.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
