人教版数学八下第19章 专题七 一次函数与二元一次方程(组)(含答案)
文档属性
| 名称 | 人教版数学八下第19章 专题七 一次函数与二元一次方程(组)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 10:42:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题七 一次函数与二元一次方程(组)
【知识清单】
1. 一次函数与二元一次方程的联系
一般地,一次函数y=kx+b 的图象上任意一点的坐标都是关于x,y 的二元一次方程kx-y+b=0 的解;以关于x,y 的二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b 的图象上,即:
2. 二元一次方程与一次函数的区别
(1)二元一次方程有两个未知数,而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未知数的关系,而一次函数既可以用一个等式表示两个变量的关系,又可以用列表法或图象法表示两个变量的关系.
3. 一次函数与二元一次方程组的对应关系
【典型例题】
1.(原创题)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(2,b).
(1)求b的值;
(2)直接写出方程组的解;
(3)根据函数图象,当0(4)若l1交x轴于点A,l2交x轴于点B,且S△PAB=9,求l2对应的函数解析式.
解:(1)将点P(2,b)的坐标代入y=x+1,得b=2+1=3.
(2)解:方程组的解为
(3)-1(4)解:S△PAB=×AB×3=9,解得AB=6.
由题易知A(-1,0),∴OA=1.
∴OB=5,∴B点的坐标为(5,0).
将点P(2,3),B(5,0)的坐标分别代入直线l2对应的函数解析式,
得解得
∴l2对应的函数解析式为y=-x+5.
【提升练习】
A级
1.若二元一次方程3x-2y=1所对应的直线是l,则下列各点不在直线l上的是( )
A.(1,1) B.(-1,1) C.(-3,-5) D.
2.如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2 的解组成的图象是( )
3.[中考·济宁]数形结合是解决数学问题常用的思想方法. 如图,直
线y=x+5 和直线y=ax+b 相交于点P,根据图象可知,方程组 的解中x 的值是( )
A.20 B.5 C.25 D.15
(第3题) (第6题)
4. [中考· 陕西] 如在同一平面直角坐标系中, 直线y= -x+4 与y=2x+m 相
交于点P (3,n), 则关于x,y 的方程组 的解为( )
5. (中考·呼和浩特)若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-x+b-1上,则常数b的值为______
6. (2019·贵阳)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是________.
7.已知一次函数y=3x+6与y=2x+b(b为常数)的图象的交点为P(-10,-24),求方程组的解和b的值.
B级
8.已知的解为则直线y=ax+b与
y=-cx+d的交点坐标为( )
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
9.小明用作图象的方法解二元一次方程组时,他作出了相应的两个一次函数的图象(如图),则他解的这个方程组是( )
A. B.
C. D.
10.直线y=kx+b过点(2,2)且与直线y=-3x相交于点(1,a),则两直线与x轴所围图形的面积为_____
11. (2020·滨州)如图,在平面直角坐标系中,直线y=-x-1与直线y=-2x+2相交于点P,两直线分别与x轴相交于点A,B.
(1)求交点P的坐标;
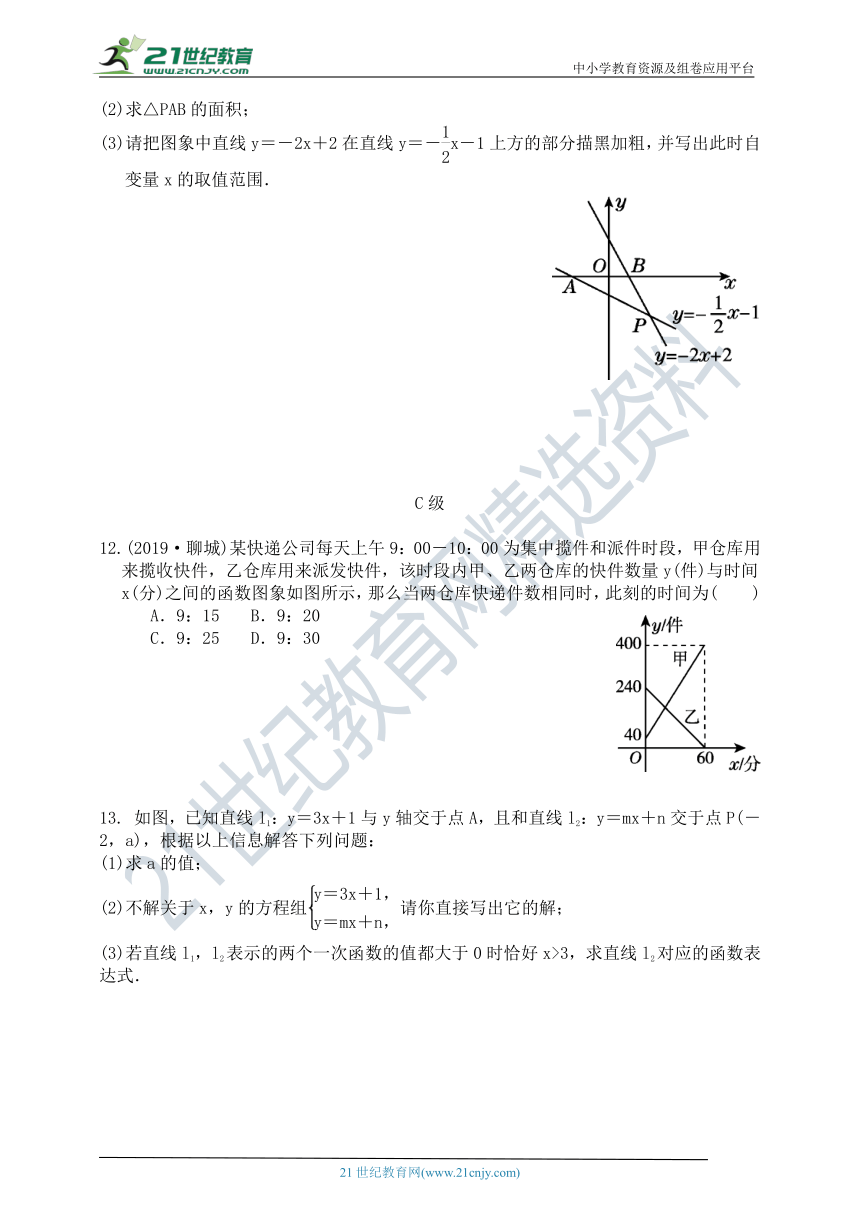
(2)求△PAB的面积;
(3)请把图象中直线y=-2x+2在直线y=-x-1上方的部分描黑加粗,并写出此时自变量x的取值范围.
C级
12.(2019·聊城)某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15 B.9:20
C.9:25 D.9:30
13. 如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
(1)求a的值;
(2)不解关于x,y的方程组请你直接写出它的解;
(3)若直线l1,l2表示的两个一次函数的值都大于0时恰好x>3,求直线l2对应的函数表达式.
答案:
A级
1.B 2.C 3.A 4. C
5. 2
7. 解:解:由题意,可得方程组的解为
将代入y=2x+b,
得-24=2×(-10)+b,
所以b=-4.
B级
8.A
9. D
10.2.4
解:∵点(1,a)在直线y=-3x上,∴a=-3.
∵直线y=kx+b过点(2,2),点(1,-3),
∴解得
∴直线y=kx+b的解析式为y=5x-8.令y=0,
则5x-8=0,
解得x=,
∴其与x轴的交点坐标为.
∵直线y=-3x经过坐标原点,
∴两直线与x轴所围图形的面积为××3=2.4.故选B.
11.解:(1)解:由解得
∴点P的坐标为(2,-2).
(2)解:在y=-x-1中,令y=0,则-x-1=0,
解得x=-2,
∴A(-2,0).在y=-2x+2中,令y=0,
则-2x+2=0,
解得x=1,∴B(1,0).∴AB=3.
∴S△PAB=AB·|yP|=×3×2=3.
(3)解:如图所示.
此时自变量x的取值范围是x<2.
C级
12.B
13. 解:(1)∵点P(-2,a)在直线y=3x+1上,
∴a=3×(-2)+1=-5.
(2)解:它的解为
(3) 解:∵直线l1,l2表示的两个一次函数的值都大于0时恰好x>3,∴直线l2过点B(3,0).
又∵直线l2过点P(-2,-5),
∴解得
∴直线l2对应的函数表达式为y=x-3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题七 一次函数与二元一次方程(组)
【知识清单】
1. 一次函数与二元一次方程的联系
一般地,一次函数y=kx+b 的图象上任意一点的坐标都是关于x,y 的二元一次方程kx-y+b=0 的解;以关于x,y 的二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b 的图象上,即:
2. 二元一次方程与一次函数的区别
(1)二元一次方程有两个未知数,而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未知数的关系,而一次函数既可以用一个等式表示两个变量的关系,又可以用列表法或图象法表示两个变量的关系.
3. 一次函数与二元一次方程组的对应关系
【典型例题】
1.(原创题)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(2,b).
(1)求b的值;
(2)直接写出方程组的解;
(3)根据函数图象,当0
解:(1)将点P(2,b)的坐标代入y=x+1,得b=2+1=3.
(2)解:方程组的解为
(3)-1
由题易知A(-1,0),∴OA=1.
∴OB=5,∴B点的坐标为(5,0).
将点P(2,3),B(5,0)的坐标分别代入直线l2对应的函数解析式,
得解得
∴l2对应的函数解析式为y=-x+5.
【提升练习】
A级
1.若二元一次方程3x-2y=1所对应的直线是l,则下列各点不在直线l上的是( )
A.(1,1) B.(-1,1) C.(-3,-5) D.
2.如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2 的解组成的图象是( )
3.[中考·济宁]数形结合是解决数学问题常用的思想方法. 如图,直
线y=x+5 和直线y=ax+b 相交于点P,根据图象可知,方程组 的解中x 的值是( )
A.20 B.5 C.25 D.15
(第3题) (第6题)
4. [中考· 陕西] 如在同一平面直角坐标系中, 直线y= -x+4 与y=2x+m 相
交于点P (3,n), 则关于x,y 的方程组 的解为( )
5. (中考·呼和浩特)若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-x+b-1上,则常数b的值为______
6. (2019·贵阳)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是________.
7.已知一次函数y=3x+6与y=2x+b(b为常数)的图象的交点为P(-10,-24),求方程组的解和b的值.
B级
8.已知的解为则直线y=ax+b与
y=-cx+d的交点坐标为( )
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
9.小明用作图象的方法解二元一次方程组时,他作出了相应的两个一次函数的图象(如图),则他解的这个方程组是( )
A. B.
C. D.
10.直线y=kx+b过点(2,2)且与直线y=-3x相交于点(1,a),则两直线与x轴所围图形的面积为_____
11. (2020·滨州)如图,在平面直角坐标系中,直线y=-x-1与直线y=-2x+2相交于点P,两直线分别与x轴相交于点A,B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=-2x+2在直线y=-x-1上方的部分描黑加粗,并写出此时自变量x的取值范围.
C级
12.(2019·聊城)某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15 B.9:20
C.9:25 D.9:30
13. 如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
(1)求a的值;
(2)不解关于x,y的方程组请你直接写出它的解;
(3)若直线l1,l2表示的两个一次函数的值都大于0时恰好x>3,求直线l2对应的函数表达式.
答案:
A级
1.B 2.C 3.A 4. C
5. 2
7. 解:解:由题意,可得方程组的解为
将代入y=2x+b,
得-24=2×(-10)+b,
所以b=-4.
B级
8.A
9. D
10.2.4
解:∵点(1,a)在直线y=-3x上,∴a=-3.
∵直线y=kx+b过点(2,2),点(1,-3),
∴解得
∴直线y=kx+b的解析式为y=5x-8.令y=0,
则5x-8=0,
解得x=,
∴其与x轴的交点坐标为.
∵直线y=-3x经过坐标原点,
∴两直线与x轴所围图形的面积为××3=2.4.故选B.
11.解:(1)解:由解得
∴点P的坐标为(2,-2).
(2)解:在y=-x-1中,令y=0,则-x-1=0,
解得x=-2,
∴A(-2,0).在y=-2x+2中,令y=0,
则-2x+2=0,
解得x=1,∴B(1,0).∴AB=3.
∴S△PAB=AB·|yP|=×3×2=3.
(3)解:如图所示.
此时自变量x的取值范围是x<2.
C级
12.B
13. 解:(1)∵点P(-2,a)在直线y=3x+1上,
∴a=3×(-2)+1=-5.
(2)解:它的解为
(3) 解:∵直线l1,l2表示的两个一次函数的值都大于0时恰好x>3,∴直线l2过点B(3,0).
又∵直线l2过点P(-2,-5),
∴解得
∴直线l2对应的函数表达式为y=x-3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
