3.2 解一元一次方程(一)——合并同类项与移项课件
文档属性
| 名称 | 3.2 解一元一次方程(一)——合并同类项与移项课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-22 00:00:00 | ||
图片预览










文档简介
课件68张PPT。请欣赏一首诗:
太阳下山晚霞红,我把鸭子赶回笼;
一半在外闹哄哄,一半的一半进笼中;
剩下十五围着我,共有多少请算清.你能列出方程来解决这个问题吗?新课导入 希腊数学家丢番图(公元3~4世纪)的墓碑上记载着:
“他的生命的六分之一是幸福童年;
再活了他生命的十二分之一,两颊长起了细细的胡须;
他结了婚,又度过了一生的七分之一;
再过五年,他有了儿子,感到很幸福;
可是儿子只活了他父亲年龄的一半;
儿子死后,他在极悲痛中度过了四年,也与世长辞了.”根据以上信息,你知道丢番图活了多少岁吗?3.2 解一元一次方程(一)
——合并同类项与移项知识与能力
1. 能根据实际问题,建立数学模型——一元一次方程,来解决;
2.能在解方程中,正确合并同类项.教学目标过程与方法
1.由实际问题引入,进一步熟悉列方程解应用题的分析步骤;
2.渗透运用数学问题来解决实际问题的建模思想.教学目标情感态度与价值观
1.通过引导发现,培养独立思考问题的能力;
2.通过学习,更加关注生活,增强用数学的意识,从而激发学习数学的热情.教学目标重点
未知数,列方程,用合并及等式性质解方程.
难点
1.建立方程时寻找“相等关系”;
2.合并时“x”或“-x”前面的系数为1或“-1”.教学重难点 约公元825年,中亚细亚数学家阿尔-花拉子米写了一本代数书, 阿拉伯文书名是‘ilm al-jabr wa’l muqabalah,直译应为《还原与对消的科学》.al-jabr 意为“还原”,这里指把负项移到方程另一端“还原”为正项;muqabalah 意即“对消”或“化简”,指方程两端可以消去相同的项或合并同类项.一般认为拉丁文中代数学一词algebra是由al-jabr演变而来. 阿尔—花拉子米
(约780——约850) (1) x-2x+4x(2)5y+y-2y(3)2a-1.5a-0.5a=(1-2+4)x=3x=(5+1 -2)y=4y=(2-1.5-0.5)a合并同类项=0实际
问题一元一次
方程 分析实际问题中的数量关系,利用其中的相等关系列出方程,是解决实际问题的一种数学方法.设未知数 列方程怎样解方程? 问题1:在一卷公元前1600年左右遗留下来的古埃及草卷中,记载者一些数学问题,其中一个问题翻译过来是:“啊哈,它的全部,它的 其和等于16”.你能求出问题中的“它”? 解:设问题中的它为x,则:它的 为 .
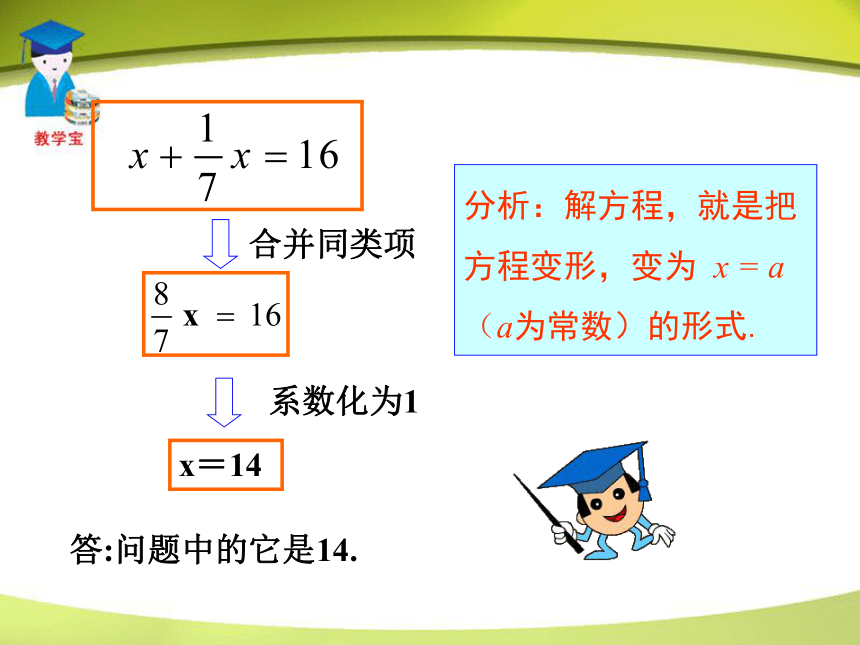
根据问题中的相等关系:它的全部+它的
=16.可列方程合并同类项系数化为1分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.答:问题中的它是14.解方程中“合并”起了什么作用? 解方程中的“合并”是利用分配律将含有未知数的项和常数项分别合并为一项.它使方程变得简单,更接近x = a的形式. 解:设计划生产Ⅰ型电视机x台,则计划生产Ⅱ型电视机15x台,计划生产Ⅲ型电视机20x台,列方程 某电视机厂今年计划生产电视机21600台,其中Ⅰ型,Ⅱ型,Ⅲ型三种电视机的数量之比为1:15:20,这三种电视机计划各生产多少台?x+15x+20x=21 600练一练 答: Ⅰ型电视机计划生产600台,Ⅱ型电视机计划生产9000台,Ⅲ型电视机计划生产12000台.合并同类项,得36x=21600系数化成1,得x=600所以
计划生产Ⅱ型电视机600×15=9000(台),
计划生产Ⅲ型电视机600×20=12000(台). 解:合并同类项,得
2x=-10
系数化为1,得
x=-5.例1:解方程(1)5x-3x=-10 解:合并同类项,得
2x=7系数化为1,得解:合并同类项,得
4x=-9
系数化为1,得(3)6x-1.5x-0.5x=-9(4)3x+5x-6x=-3×4+20解:合并同类项,得
2x=8.
系数化为1,得
x=4.(1)-2x-0.5x=-10;
(2)3x-4x=-15+10;
(4)-4x+5x-3x=3.5×3-6x=4x=5练一练解下列方程 1.简单方程解法步骤 移项;
合并同类项;
系数化为1.归纳 问题2:有一批学生去游玩,若每辆车坐43人,则还有35人没座;若每辆车坐45 人,则还有15人没座,求有多少辆车,多少学生? 解:设有x辆车.
每辆车坐43人,共有43x人,加上没座的35人,共有学生43x+35.
若每辆车坐45人,共有45x人,加上没座的15人,共有学生45x+15.
找相等关系:学生的总人数是一个定值,表示它的两个式子应相等,所以列方程
43x+35= 45x+15怎样解方程?43x+35= 45x+1543x-45x=15-3543x+35-35-45x=45x+15-35-45x等式性质1 把等式一边的某一项变号后移到另一边.你发现了什么?移项合并同类项系数化成1答:有10辆车,465个学生.所以学生总人数为:43×10+35=465(人).移项
把等式一边的某项变号后移到另一边,叫做移项.知识要点 通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式. 以上解方程中“移项”起了什么作用? 下面的移项对不对?如果不对,请改正?(1)从5+2x=10,得2x=10+5 (2)从3x=2x-5,得3x+2x=5 (3) 从-2x+5=1-3x,得-2x+3x=1+5 2x=10-53x-2x=-5-2x+3x=1-5练一练下列移项正确的是( )
A.由2+x=8,得到x=8+2
B.由5x=-8+x,得到5x+x= -8
C.由4x=2x+1,得到4x-2x=1
D.由5x-3=0,得到5x=-3C练一练例2:解下列方程.解:移项,得6x-3x=8+7合并同类项,得3x=15.系数化为1,得x=5.移项时应注意改变项的符号解:移项,得合并同类项,得系数化成1,得解下列方程 .(1)10x-4=6(2)5x-7=3x - 5x=1x=1练一练解方程的步骤及依据:
1.移项(等式的性质1)
合并(分配律)
系数化为1(等式的性质2)
2.“对消”与“还原”就是“合并”与“移项”
3.表示同一量的两个不同式子相等. 归纳 现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗?“对消”与“还原”就是“合并”与“移项”. 下面方程的解法对吗?如果不对,应怎样改正?解:移项,得 合并同类项,得 系数化为1,得 1.移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边;
2.移项要改变符号. 注意 例3:有一列数,按一定的规律成-1,2,-4,8,-16,32, -64,···,其中某三个相邻数的和为1 536,这三个数各是多少? 解:设这三个相邻数中的第1个数为x,
那么第2个数就是-2x,
第3个数就是-2×(-2x)=4x.
根据这三个数的和是1536,得
x-2x+4x=1 536.合并同类项,得
3x=1 536.
系数化为1,得
x=512.
所以 -2x=-1 024,
4x=2 048.
答:这三个数是512、-1 024、2 048. 1.有一列数,按一定规律排列成1,-5,25,-125···若其中某三个相邻数的和是13 125,这三个数各是多少 ?练一练解:设这三个相邻数中的第1个数为x,
那么第2个数就是-5x,
第3个数就是-5×(-5x)=25x.
根据这三个数的和是13 125,得
x-5x+25x=13 125.合并同类项,得
19x=13 125.
系数化为1,得
x=625.
所以 -5x= -3 125,
25x= 15 625.
答:这三个数是625、 -3 125 、 15 625. 2.三个连续的奇数的和是27,求这三个奇数. 解:设这三个相奇数中的第2个数为x,
那么第1个数就是x-2,
第3个数就是 x+2.
根据这三个数的和是27,得
(x-2)+ x+ x+2=27
解,得 x=9
所以第第1个数就是x-2=9-2=7;
第3个数就是 x+2=9+2=11.
答:这3个奇数是7,9,11.解:设这三个相奇数中的第2个数为x,
那么第1个数就是x-2,
第3个数就是 x+2.
根据这三个数的和是29,得
(x-2)+ x+ x+2=29
解,得 x=
因为 不是奇数,所以不存在这样的三个奇数. 3.如果三个连续奇数的和是29,你能求出这三个奇数吗? 4.在某月内,李老师要参加三天的学习培训,现在知道这三天的日期的数字之和是39.
(1)培训时间是连续的三天,你知道这几天分别是当月的哪几号吗?
(2)若培训时间是连续三周的周六,那这几天又分是当月的哪几号? (1)12、13、14(2)6、13、20 例4:根据下面的两种移动电话计费方式表,考虑下列问题. (1)一个月本地通话时间150分和300分,计算按两种移动电话计费方式各需要交费多少元?
(2)会出现两种移动电话计费方式收费一样吗? 解:(1) (2)设累计通话t分,则按方式一要收费(50+0.3t)元,按方式二要收费(10+0.4t).如果两种移动电话计费方式收费一样,
则 50+0.3t= 10+0.4t
移项,得 0.3t-0.4t=10-50
合并同类项,得 -0.1t=-40.
系数化为1,得 t=400.
由上可知,如果一个月内通话400分,那么两种计费方式的收费一样. (1)8人分别乘两辆小汽车赶往火车站,其中一辆小汽车在距离火车站15千米的地方出了故障,此时离火车停止检票时间还有42分,这时唯一可以利用的交通工具只有一辆小汽车,连司机在内限乘5人,这辆小汽车的平均速度为60千米/时,这8人能赶上火车吗?(设走行速度为5千米/时).练一练第一种情况:
小汽车分二批送这8人,若第二批人在原地不动,那么小汽车来回要走15×3=45千米,所需
时间为 =45分>42分,因此,单靠汽车来回接送无法使8人都赶上火车.
第二种情况:
若在汽车送第一批人的同时,其他人先步行,可以节省时间,汽车送完第一批人后,用了x解:此题可分类讨论:小时与第二批人相遇,再用x小时送到火车站,则列方程得,解得:所用时间为: 时,
因为40.4<42,因此,这时8人能赶上火车.第三种情况:
这辆汽车行驶到途中一定位置时放下第一批人,然后掉头再接另一批人,使得两批人同时到达火车站,那么这时所用时间更少. (2)一位老商人在临死前,把他的儿子叫到床前,他要把他一生积蓄的金币分给儿子们,让大儿子拿出一枚金币后,再把盘里的 分给他;然后让二儿子拿二枚金币后,再分盘里的 给他;让二儿子拿三枚金币后,再分盘里的 给他···照这样分法分下去,让最后一个儿子拿完金币后,金币恰好分完,面且每个儿子得到的金币数相等,请你算一算,老商人一生攒了多少枚金币?他共有几个儿子? 分析:设老商人共积攒x枚金币,大儿子拿出一枚后,盘里还剩(x-1)枚,大儿子又拿了盘中的 ,因此大儿子共得金币 枚.此时盘中剩 枚,被二儿子拿走二枚后,盘中还剩 枚.二儿子又分得此时盘中的 ,因此二儿子共得到金币 枚 .根据所有儿子得到的金币都相等,可列出方程. 解:设老商人一生积攒了x枚金币,
列方程去括号,得移项,得合并同类项,得系数化为1,得x=36.即老商人共有36枚金币,大儿子分得
因为所有儿子分得的金币数都相等,
因此老商人有 答:老商人一生积攒了36枚金币,他共有6个儿子.用一元一次方程分析并解决实际问题的基本过程:实际问题数学问题
(一元一次方程)实际问题
的答案数学问题的解
(x=a)检验列方程解方程归纳 1.简单方程解法步骤 移项;
合并同类项;
系数化为1.课堂小结2.用一元一次方程分析并解决实际问题的基本过程:实际问题数学问题
(一元一次方程)实际问题
的答案数学问题的解
(x=a)检验列方程解方程 1. 若方程x+9=8的解也是方程ax+3=7解,则a=_________.
2.若x=4是方程 的解,则
的值为__________.-410随堂练习3.解下列方程.x=1x=4x=-12x=1 4.已知:y1 = 2x+1, y2 = 4 -x.当x取何值时, y1 = y2 ? 解:由题意,得
2x+1= 4 -x
移项,得
2x+x=4-1
合并同类项,得
3x=3
系数化为1,得
x=1.
所以当x=1时, y1 = y2 . 5. 有一人问老师,他所教的班级有多少学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足六位学生正在操场踢足球.”你知道这个班有多少学生吗? 解:设这个班有x个学生,
列方程移项,得合并同类项,得系数化为1,得x=56.答:这个班有56个学生. 6. 小明和小刚每天早晨坚持跑步,小明每秒跑4米,小刚每秒跑6米.
(1)若他们站在百米跑道的两端同时相向起跑,那么几秒后相遇?
(2)若小明站在百米起点处,小刚站在他前面10米处,两人同时同向起跑,几秒后小明追上小刚?解:(1)设x秒后相遇.可得方程:
6x+4x=100
合并同类项,得
10x=100
系数化为1,得
x=10.
答:两人10秒后相遇.(2)设小明x秒后追上小刚.可得方程:
4x+10=6x
移项,得
4x-6x=-10
合并同类项,得
-2x=-10
系数化为1,得
x=5.
答:小明5秒后追上小刚.习题答案
太阳下山晚霞红,我把鸭子赶回笼;
一半在外闹哄哄,一半的一半进笼中;
剩下十五围着我,共有多少请算清.你能列出方程来解决这个问题吗?新课导入 希腊数学家丢番图(公元3~4世纪)的墓碑上记载着:
“他的生命的六分之一是幸福童年;
再活了他生命的十二分之一,两颊长起了细细的胡须;
他结了婚,又度过了一生的七分之一;
再过五年,他有了儿子,感到很幸福;
可是儿子只活了他父亲年龄的一半;
儿子死后,他在极悲痛中度过了四年,也与世长辞了.”根据以上信息,你知道丢番图活了多少岁吗?3.2 解一元一次方程(一)
——合并同类项与移项知识与能力
1. 能根据实际问题,建立数学模型——一元一次方程,来解决;
2.能在解方程中,正确合并同类项.教学目标过程与方法
1.由实际问题引入,进一步熟悉列方程解应用题的分析步骤;
2.渗透运用数学问题来解决实际问题的建模思想.教学目标情感态度与价值观
1.通过引导发现,培养独立思考问题的能力;
2.通过学习,更加关注生活,增强用数学的意识,从而激发学习数学的热情.教学目标重点
未知数,列方程,用合并及等式性质解方程.
难点
1.建立方程时寻找“相等关系”;
2.合并时“x”或“-x”前面的系数为1或“-1”.教学重难点 约公元825年,中亚细亚数学家阿尔-花拉子米写了一本代数书, 阿拉伯文书名是‘ilm al-jabr wa’l muqabalah,直译应为《还原与对消的科学》.al-jabr 意为“还原”,这里指把负项移到方程另一端“还原”为正项;muqabalah 意即“对消”或“化简”,指方程两端可以消去相同的项或合并同类项.一般认为拉丁文中代数学一词algebra是由al-jabr演变而来. 阿尔—花拉子米
(约780——约850) (1) x-2x+4x(2)5y+y-2y(3)2a-1.5a-0.5a=(1-2+4)x=3x=(5+1 -2)y=4y=(2-1.5-0.5)a合并同类项=0实际
问题一元一次
方程 分析实际问题中的数量关系,利用其中的相等关系列出方程,是解决实际问题的一种数学方法.设未知数 列方程怎样解方程? 问题1:在一卷公元前1600年左右遗留下来的古埃及草卷中,记载者一些数学问题,其中一个问题翻译过来是:“啊哈,它的全部,它的 其和等于16”.你能求出问题中的“它”? 解:设问题中的它为x,则:它的 为 .
根据问题中的相等关系:它的全部+它的
=16.可列方程合并同类项系数化为1分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.答:问题中的它是14.解方程中“合并”起了什么作用? 解方程中的“合并”是利用分配律将含有未知数的项和常数项分别合并为一项.它使方程变得简单,更接近x = a的形式. 解:设计划生产Ⅰ型电视机x台,则计划生产Ⅱ型电视机15x台,计划生产Ⅲ型电视机20x台,列方程 某电视机厂今年计划生产电视机21600台,其中Ⅰ型,Ⅱ型,Ⅲ型三种电视机的数量之比为1:15:20,这三种电视机计划各生产多少台?x+15x+20x=21 600练一练 答: Ⅰ型电视机计划生产600台,Ⅱ型电视机计划生产9000台,Ⅲ型电视机计划生产12000台.合并同类项,得36x=21600系数化成1,得x=600所以
计划生产Ⅱ型电视机600×15=9000(台),
计划生产Ⅲ型电视机600×20=12000(台). 解:合并同类项,得
2x=-10
系数化为1,得
x=-5.例1:解方程(1)5x-3x=-10 解:合并同类项,得
2x=7系数化为1,得解:合并同类项,得
4x=-9
系数化为1,得(3)6x-1.5x-0.5x=-9(4)3x+5x-6x=-3×4+20解:合并同类项,得
2x=8.
系数化为1,得
x=4.(1)-2x-0.5x=-10;
(2)3x-4x=-15+10;
(4)-4x+5x-3x=3.5×3-6x=4x=5练一练解下列方程 1.简单方程解法步骤 移项;
合并同类项;
系数化为1.归纳 问题2:有一批学生去游玩,若每辆车坐43人,则还有35人没座;若每辆车坐45 人,则还有15人没座,求有多少辆车,多少学生? 解:设有x辆车.
每辆车坐43人,共有43x人,加上没座的35人,共有学生43x+35.
若每辆车坐45人,共有45x人,加上没座的15人,共有学生45x+15.
找相等关系:学生的总人数是一个定值,表示它的两个式子应相等,所以列方程
43x+35= 45x+15怎样解方程?43x+35= 45x+1543x-45x=15-3543x+35-35-45x=45x+15-35-45x等式性质1 把等式一边的某一项变号后移到另一边.你发现了什么?移项合并同类项系数化成1答:有10辆车,465个学生.所以学生总人数为:43×10+35=465(人).移项
把等式一边的某项变号后移到另一边,叫做移项.知识要点 通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式. 以上解方程中“移项”起了什么作用? 下面的移项对不对?如果不对,请改正?(1)从5+2x=10,得2x=10+5 (2)从3x=2x-5,得3x+2x=5 (3) 从-2x+5=1-3x,得-2x+3x=1+5 2x=10-53x-2x=-5-2x+3x=1-5练一练下列移项正确的是( )
A.由2+x=8,得到x=8+2
B.由5x=-8+x,得到5x+x= -8
C.由4x=2x+1,得到4x-2x=1
D.由5x-3=0,得到5x=-3C练一练例2:解下列方程.解:移项,得6x-3x=8+7合并同类项,得3x=15.系数化为1,得x=5.移项时应注意改变项的符号解:移项,得合并同类项,得系数化成1,得解下列方程 .(1)10x-4=6(2)5x-7=3x - 5x=1x=1练一练解方程的步骤及依据:
1.移项(等式的性质1)
合并(分配律)
系数化为1(等式的性质2)
2.“对消”与“还原”就是“合并”与“移项”
3.表示同一量的两个不同式子相等. 归纳 现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗?“对消”与“还原”就是“合并”与“移项”. 下面方程的解法对吗?如果不对,应怎样改正?解:移项,得 合并同类项,得 系数化为1,得 1.移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边;
2.移项要改变符号. 注意 例3:有一列数,按一定的规律成-1,2,-4,8,-16,32, -64,···,其中某三个相邻数的和为1 536,这三个数各是多少? 解:设这三个相邻数中的第1个数为x,
那么第2个数就是-2x,
第3个数就是-2×(-2x)=4x.
根据这三个数的和是1536,得
x-2x+4x=1 536.合并同类项,得
3x=1 536.
系数化为1,得
x=512.
所以 -2x=-1 024,
4x=2 048.
答:这三个数是512、-1 024、2 048. 1.有一列数,按一定规律排列成1,-5,25,-125···若其中某三个相邻数的和是13 125,这三个数各是多少 ?练一练解:设这三个相邻数中的第1个数为x,
那么第2个数就是-5x,
第3个数就是-5×(-5x)=25x.
根据这三个数的和是13 125,得
x-5x+25x=13 125.合并同类项,得
19x=13 125.
系数化为1,得
x=625.
所以 -5x= -3 125,
25x= 15 625.
答:这三个数是625、 -3 125 、 15 625. 2.三个连续的奇数的和是27,求这三个奇数. 解:设这三个相奇数中的第2个数为x,
那么第1个数就是x-2,
第3个数就是 x+2.
根据这三个数的和是27,得
(x-2)+ x+ x+2=27
解,得 x=9
所以第第1个数就是x-2=9-2=7;
第3个数就是 x+2=9+2=11.
答:这3个奇数是7,9,11.解:设这三个相奇数中的第2个数为x,
那么第1个数就是x-2,
第3个数就是 x+2.
根据这三个数的和是29,得
(x-2)+ x+ x+2=29
解,得 x=
因为 不是奇数,所以不存在这样的三个奇数. 3.如果三个连续奇数的和是29,你能求出这三个奇数吗? 4.在某月内,李老师要参加三天的学习培训,现在知道这三天的日期的数字之和是39.
(1)培训时间是连续的三天,你知道这几天分别是当月的哪几号吗?
(2)若培训时间是连续三周的周六,那这几天又分是当月的哪几号? (1)12、13、14(2)6、13、20 例4:根据下面的两种移动电话计费方式表,考虑下列问题. (1)一个月本地通话时间150分和300分,计算按两种移动电话计费方式各需要交费多少元?
(2)会出现两种移动电话计费方式收费一样吗? 解:(1) (2)设累计通话t分,则按方式一要收费(50+0.3t)元,按方式二要收费(10+0.4t).如果两种移动电话计费方式收费一样,
则 50+0.3t= 10+0.4t
移项,得 0.3t-0.4t=10-50
合并同类项,得 -0.1t=-40.
系数化为1,得 t=400.
由上可知,如果一个月内通话400分,那么两种计费方式的收费一样. (1)8人分别乘两辆小汽车赶往火车站,其中一辆小汽车在距离火车站15千米的地方出了故障,此时离火车停止检票时间还有42分,这时唯一可以利用的交通工具只有一辆小汽车,连司机在内限乘5人,这辆小汽车的平均速度为60千米/时,这8人能赶上火车吗?(设走行速度为5千米/时).练一练第一种情况:
小汽车分二批送这8人,若第二批人在原地不动,那么小汽车来回要走15×3=45千米,所需
时间为 =45分>42分,因此,单靠汽车来回接送无法使8人都赶上火车.
第二种情况:
若在汽车送第一批人的同时,其他人先步行,可以节省时间,汽车送完第一批人后,用了x解:此题可分类讨论:小时与第二批人相遇,再用x小时送到火车站,则列方程得,解得:所用时间为: 时,
因为40.4<42,因此,这时8人能赶上火车.第三种情况:
这辆汽车行驶到途中一定位置时放下第一批人,然后掉头再接另一批人,使得两批人同时到达火车站,那么这时所用时间更少. (2)一位老商人在临死前,把他的儿子叫到床前,他要把他一生积蓄的金币分给儿子们,让大儿子拿出一枚金币后,再把盘里的 分给他;然后让二儿子拿二枚金币后,再分盘里的 给他;让二儿子拿三枚金币后,再分盘里的 给他···照这样分法分下去,让最后一个儿子拿完金币后,金币恰好分完,面且每个儿子得到的金币数相等,请你算一算,老商人一生攒了多少枚金币?他共有几个儿子? 分析:设老商人共积攒x枚金币,大儿子拿出一枚后,盘里还剩(x-1)枚,大儿子又拿了盘中的 ,因此大儿子共得金币 枚.此时盘中剩 枚,被二儿子拿走二枚后,盘中还剩 枚.二儿子又分得此时盘中的 ,因此二儿子共得到金币 枚 .根据所有儿子得到的金币都相等,可列出方程. 解:设老商人一生积攒了x枚金币,
列方程去括号,得移项,得合并同类项,得系数化为1,得x=36.即老商人共有36枚金币,大儿子分得
因为所有儿子分得的金币数都相等,
因此老商人有 答:老商人一生积攒了36枚金币,他共有6个儿子.用一元一次方程分析并解决实际问题的基本过程:实际问题数学问题
(一元一次方程)实际问题
的答案数学问题的解
(x=a)检验列方程解方程归纳 1.简单方程解法步骤 移项;
合并同类项;
系数化为1.课堂小结2.用一元一次方程分析并解决实际问题的基本过程:实际问题数学问题
(一元一次方程)实际问题
的答案数学问题的解
(x=a)检验列方程解方程 1. 若方程x+9=8的解也是方程ax+3=7解,则a=_________.
2.若x=4是方程 的解,则
的值为__________.-410随堂练习3.解下列方程.x=1x=4x=-12x=1 4.已知:y1 = 2x+1, y2 = 4 -x.当x取何值时, y1 = y2 ? 解:由题意,得
2x+1= 4 -x
移项,得
2x+x=4-1
合并同类项,得
3x=3
系数化为1,得
x=1.
所以当x=1时, y1 = y2 . 5. 有一人问老师,他所教的班级有多少学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足六位学生正在操场踢足球.”你知道这个班有多少学生吗? 解:设这个班有x个学生,
列方程移项,得合并同类项,得系数化为1,得x=56.答:这个班有56个学生. 6. 小明和小刚每天早晨坚持跑步,小明每秒跑4米,小刚每秒跑6米.
(1)若他们站在百米跑道的两端同时相向起跑,那么几秒后相遇?
(2)若小明站在百米起点处,小刚站在他前面10米处,两人同时同向起跑,几秒后小明追上小刚?解:(1)设x秒后相遇.可得方程:
6x+4x=100
合并同类项,得
10x=100
系数化为1,得
x=10.
答:两人10秒后相遇.(2)设小明x秒后追上小刚.可得方程:
4x+10=6x
移项,得
4x-6x=-10
合并同类项,得
-2x=-10
系数化为1,得
x=5.
答:小明5秒后追上小刚.习题答案
