鲁教版(五四学制)六年级下册第六章 整式的乘除:第9讲完全平方公式(32张PPT)
文档属性
| 名称 | 鲁教版(五四学制)六年级下册第六章 整式的乘除:第9讲完全平方公式(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 09:43:47 | ||
图片预览









文档简介
(共32张PPT)
完全平方公式
1
情境导入
来三个,就给每人三块糖,……
来一个同学,就给这个同学一块糖;
来两个同学,给每人两块糖;
(1)第一天一起来了 a 个男生,老师一共要分多少块?
(2)第二天来了b个女生,又该分多少块?
(3)如果第三天来了(a+b)个学生呢?
?
第三天分得糖果数与前两天分得总和一样多吗?为什么?
思考:
合作探究
2
活动探究一
2
1.利用整式乘法来推导
(a+b)2
=(a+b)(a+b)
(a+b)2
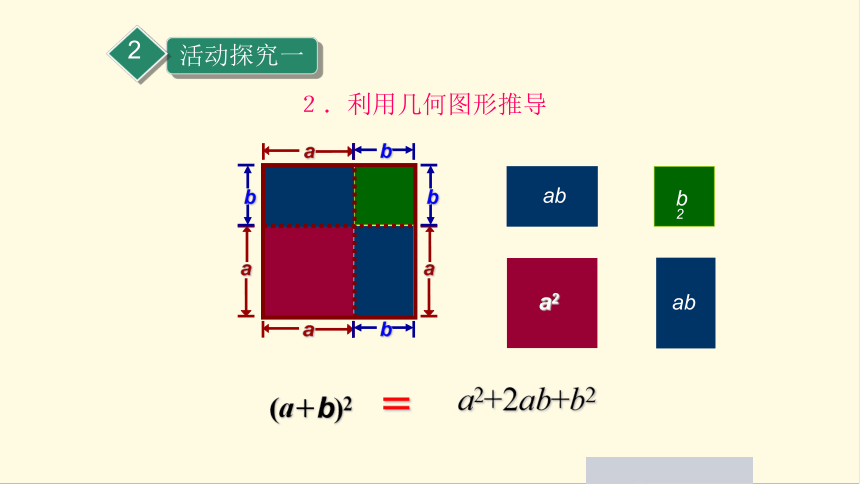
2.利用几何图形推导
a
a
b
b
a2
ab
ab
b2
a2
ab
ab
b2
a
b
a
b
a2+2ab+b2
=
活动探究一
2
∵(a+b)2=a2+2ab+b2
第三天得到的糖果数与前两天
得到的总和一样多吗?为什么
活动探究一
2
?
(a-b)2=
方法1:利用整式的乘法推导
(a b)2
活动探究 二
2
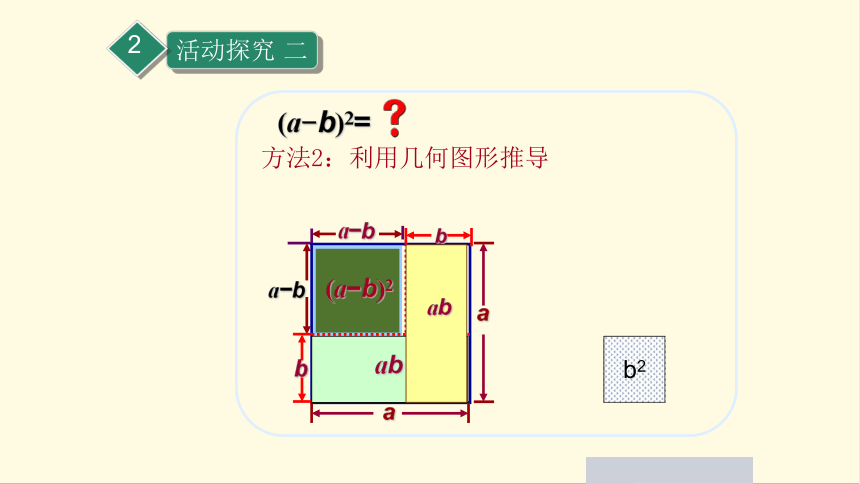
(a-b)2=
方法2:利用几何图形推导
a b
a b
a
a
b
b
(a b)2
ab
ab
b2
活动探究 二
2
(a-b)2=
方法1:利用整式的乘法推导
方法2:利用几何图形推导
方法3:将(a-b)2看成[a+(-b)]2
a2 2ab+b2
活动探究 二
2
= a2 +2 a(-b) +(-b)2
[a+(-b)]2
=
a2 2ab+b2
完全平方公式
(a+b)2=a2+2ab+b2
(a b)2= a2-2ab+b2
【提问】它们有何相同点和不同点?
两数和(或差)的平方,等于它们的平方和,
加上(或减去)它们的积的2倍.
观察建模
3
你能用自己的语言叙述这两个公式吗?
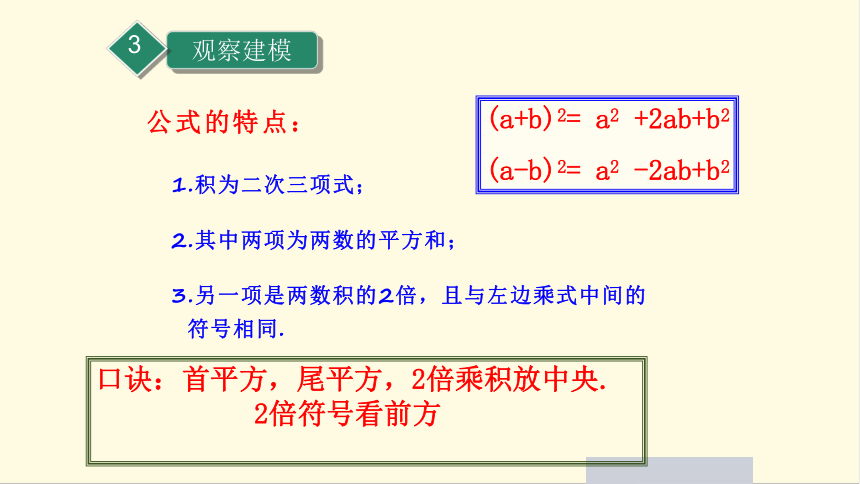
公式的特点:
1.积为二次三项式;
2.其中两项为两数的平方和;
3.另一项是两数积的2倍,且与左边乘式中间的符号相同.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 -2ab+b2
观察建模
3
口诀:首平方,尾平方,2倍乘积放中央.
2倍符号看前方
口答:
1. (p+q)2=_____+2· __· __ +_____
2. (m-n)2=_____–_____+_____
3. (a-1)2 = ____( )2· __ ·__+_____
4. (2+b)2 =____+_____( )_____
学以致用
4
p2
p
q
q2
m2
n2
2mn
a2
–
a
1
12
22
b2
+
2 2 b
·
·
纠错练习.指出下列各式中的错误,并加以改正:
观察建模
3
【例1】运用完全平方公式计算:
学以致用
4
学以致用
4
【例2】下列各式中可以运用完全平方公式计算的有: ,并把它计算出来。
(1)
(2)
(3)
从这组练习题中你发现了什么?
巩固提高
5
平方差公式
完全平方公式
一同一反
两反
两同
完全平方公式和平方差公式不同:
形式不同:
结果不同:
完全平方公式的结果是三项,
平方差公式的结果是两项。
巩固提高
5
巩固提高
5
-4m2-4mn-n2
1.这节课我们学到了什么?
2.在推导公式时,运用了哪些的方法?
3.通过这个推导过程,有什么体会?
反思小结
7
(2019·宜昌)化简(x-3)2 - x(x-6)的结果为( ).
A.6x-9 B.-12x+9 C.9 D.3x+9
【答案】C
【解析】解:(x-3)2 - x(x-6)
=x2-2×3x+32-x2+6x
=x2-6x+9-x2+6x
=9
【点睛】考查完全平方公式,单项式乘多项式.
C
完成填空x2+y2=(x+y)2- =(x- y)2+ .
解:由(x+y)2=x2+2xy+y2,
(x- y)2=x2- 2xy+y2
可知x2+y2=(x+y)2- 2xy=(x- y)2+2xy.
故两空格都填入2xy
(1)两个公式的左边都是一个二项式的完全平方的形式:两者仅有一个“符号”不同
(2)两个公式的右边都是二次三项式,其中有两项是公式左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍,两者也仅有一个“符号”不同
(3)公式中的字母a,b可以表示任意代数式。,b可以表示数,单项式和多项式。
课堂总结
1.完全平方公式的字母表示为:
2.完全平方公式的语言描述:
(a+b)2=a2+2ab+b2;
(a- b)2=a2- 2ab+b2.
两数和(或差)的平方,等于这两数的平方和加上(或减去)这两数积的两倍
3.完全平方公式的特点
练习
8
一、填空
1.(x+3y)2=______,( )2=y2-2y+1.
2.( )2=9a2 - ________+16b2,
x2+10x+______=(x+_____)2.
反思小结
7
3.(a-b)2+________=(a+b)2,
x2+ -2________=(x-_____)2.
4.如果a2+ma+9是一个完全平方式,那么m=_________.
5.(x+y-z)(x-y+z)=___________.
6.一个正方形的边长增加2cm,它的面积就增加12cm2,这个正方形的边长是___________.
练习
8
7.若 , 则 =( )
A.-2 B.-1 C.1 D.2
8.已知x-y=4,xy=12,则x2+y2的值是( )
A.28 B.40 C.26 D.25
思想
数形结合
整式乘法
转化
类比
(a+b)2=a2+2ab+b2
(a b)2= a2-2ab+b2
(a+b)(a-b)=a2-b2
反思小结
7
完全平方公式
1
情境导入
来三个,就给每人三块糖,……
来一个同学,就给这个同学一块糖;
来两个同学,给每人两块糖;
(1)第一天一起来了 a 个男生,老师一共要分多少块?
(2)第二天来了b个女生,又该分多少块?
(3)如果第三天来了(a+b)个学生呢?
?
第三天分得糖果数与前两天分得总和一样多吗?为什么?
思考:
合作探究
2
活动探究一
2
1.利用整式乘法来推导
(a+b)2
=(a+b)(a+b)
(a+b)2
2.利用几何图形推导
a
a
b
b
a2
ab
ab
b2
a2
ab
ab
b2
a
b
a
b
a2+2ab+b2
=
活动探究一
2
∵(a+b)2=a2+2ab+b2
第三天得到的糖果数与前两天
得到的总和一样多吗?为什么
活动探究一
2
?
(a-b)2=
方法1:利用整式的乘法推导
(a b)2
活动探究 二
2
(a-b)2=
方法2:利用几何图形推导
a b
a b
a
a
b
b
(a b)2
ab
ab
b2
活动探究 二
2
(a-b)2=
方法1:利用整式的乘法推导
方法2:利用几何图形推导
方法3:将(a-b)2看成[a+(-b)]2
a2 2ab+b2
活动探究 二
2
= a2 +2 a(-b) +(-b)2
[a+(-b)]2
=
a2 2ab+b2
完全平方公式
(a+b)2=a2+2ab+b2
(a b)2= a2-2ab+b2
【提问】它们有何相同点和不同点?
两数和(或差)的平方,等于它们的平方和,
加上(或减去)它们的积的2倍.
观察建模
3
你能用自己的语言叙述这两个公式吗?
公式的特点:
1.积为二次三项式;
2.其中两项为两数的平方和;
3.另一项是两数积的2倍,且与左边乘式中间的符号相同.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 -2ab+b2
观察建模
3
口诀:首平方,尾平方,2倍乘积放中央.
2倍符号看前方
口答:
1. (p+q)2=_____+2· __· __ +_____
2. (m-n)2=_____–_____+_____
3. (a-1)2 = ____( )2· __ ·__+_____
4. (2+b)2 =____+_____( )_____
学以致用
4
p2
p
q
q2
m2
n2
2mn
a2
–
a
1
12
22
b2
+
2 2 b
·
·
纠错练习.指出下列各式中的错误,并加以改正:
观察建模
3
【例1】运用完全平方公式计算:
学以致用
4
学以致用
4
【例2】下列各式中可以运用完全平方公式计算的有: ,并把它计算出来。
(1)
(2)
(3)
从这组练习题中你发现了什么?
巩固提高
5
平方差公式
完全平方公式
一同一反
两反
两同
完全平方公式和平方差公式不同:
形式不同:
结果不同:
完全平方公式的结果是三项,
平方差公式的结果是两项。
巩固提高
5
巩固提高
5
-4m2-4mn-n2
1.这节课我们学到了什么?
2.在推导公式时,运用了哪些的方法?
3.通过这个推导过程,有什么体会?
反思小结
7
(2019·宜昌)化简(x-3)2 - x(x-6)的结果为( ).
A.6x-9 B.-12x+9 C.9 D.3x+9
【答案】C
【解析】解:(x-3)2 - x(x-6)
=x2-2×3x+32-x2+6x
=x2-6x+9-x2+6x
=9
【点睛】考查完全平方公式,单项式乘多项式.
C
完成填空x2+y2=(x+y)2- =(x- y)2+ .
解:由(x+y)2=x2+2xy+y2,
(x- y)2=x2- 2xy+y2
可知x2+y2=(x+y)2- 2xy=(x- y)2+2xy.
故两空格都填入2xy
(1)两个公式的左边都是一个二项式的完全平方的形式:两者仅有一个“符号”不同
(2)两个公式的右边都是二次三项式,其中有两项是公式左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍,两者也仅有一个“符号”不同
(3)公式中的字母a,b可以表示任意代数式。,b可以表示数,单项式和多项式。
课堂总结
1.完全平方公式的字母表示为:
2.完全平方公式的语言描述:
(a+b)2=a2+2ab+b2;
(a- b)2=a2- 2ab+b2.
两数和(或差)的平方,等于这两数的平方和加上(或减去)这两数积的两倍
3.完全平方公式的特点
练习
8
一、填空
1.(x+3y)2=______,( )2=y2-2y+1.
2.( )2=9a2 - ________+16b2,
x2+10x+______=(x+_____)2.
反思小结
7
3.(a-b)2+________=(a+b)2,
x2+ -2________=(x-_____)2.
4.如果a2+ma+9是一个完全平方式,那么m=_________.
5.(x+y-z)(x-y+z)=___________.
6.一个正方形的边长增加2cm,它的面积就增加12cm2,这个正方形的边长是___________.
练习
8
7.若 , 则 =( )
A.-2 B.-1 C.1 D.2
8.已知x-y=4,xy=12,则x2+y2的值是( )
A.28 B.40 C.26 D.25
思想
数形结合
整式乘法
转化
类比
(a+b)2=a2+2ab+b2
(a b)2= a2-2ab+b2
(a+b)(a-b)=a2-b2
反思小结
7
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
