12.2 证明 课件(共33张PPT)
文档属性
| 名称 | 12.2 证明 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 32.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
12.2 证明
Proof
苏科版七年级下册第12章证明
教学目标
01
了解证明、定理与定理的推论的含义,认识九个基本事实
02
掌握证明的一般步骤与书写规范
知识精讲
情境引入
01
视觉误差~
是静的,还是动的?
知识精讲
情境引入
01
视觉误差~
左右两边处于中心位置的圆大小是否相等?
知识精讲
情境引入
01
观察、操作、实验是人们认识事物的重要手段,通过观察、操作、实验,常常可以探索发现一些结论,但是这些结论不一定正确,数学中,探索发现的结论需要加以证实.
知识精讲
情境引入
01
Q1:如图,两条线段AB与CD哪一条长一些?
通过度量线段AB、CD的长度,可以证实:线段CD比线段AB长,故以上结论不正确.
看上去线段AB比线段CD长
But
C B D
A
知识精讲
情境引入
01
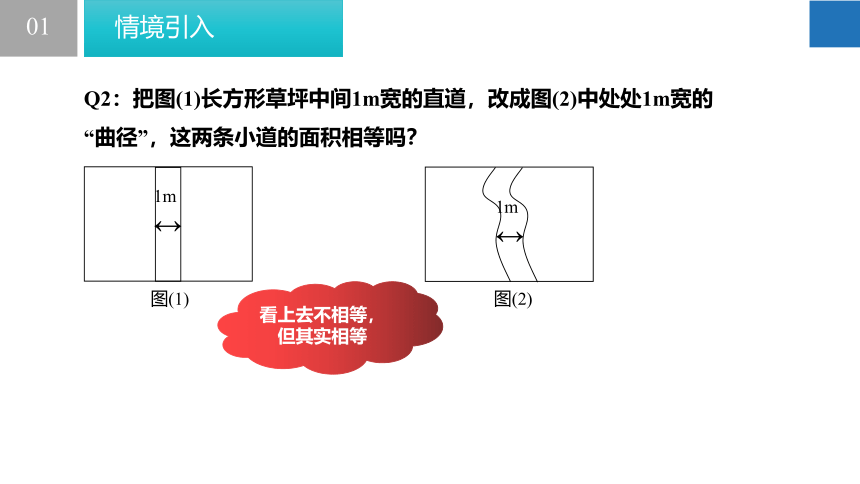
Q2:把图(1)长方形草坪中间1m宽的直道,改成图(2)中处处1m宽的“曲径”,这两条小道的面积相等吗?
1m
1m
图(1) 图(2)
看上去不相等,但其实相等
知识精讲
情境引入
01
【分析】
如果将图(2)中小道左边的草坪向右平移1m,并将其与右边的草坪拼在一起,那么得到一个长为(a-1)m、宽为bm的长方形.
于是,“曲径”的面积,
即“原长方形的面积”-“现长方形的面积
=ab-b(a-1)=ab-ab+b=b(m );
而“直道”的面积=1×b=b(m );
1m
图(2)
∴通过图形的平移与计算可得:
两条小道的面积相等.
知识精讲
情境引入
01
Q3:当x=-5、-0.5、0、2、3时,分别计算代数式x -2x+2的值,你发现了什么?
x取不同的值,
x -2x+2的值都是正数
x x -2x+2
-5 37
-0.5 3.25
0 2
2 2
3 5
知识精讲
情境引入
01
【分析】
x -2x+2=(x -2x+1)+1=(x-1) +1,
∵(x-1) ≥0,
∴(x-1) +1≥1.
∴通过将x -2x+2变形为(x-1) +1可证:
不管x取何值,代数式的值都不小于1.
知识精讲
情境引入
01
Q4:图(1)是一张8×8的正方形纸片,把它剪成4块,按图(2)重新拼合.
这4块纸片恰好能拼成一个长为13、宽为5的长方形吗?
看上去能,但其实不能,图(2)本身就画得不对
知识精讲
情境引入
01
【分析】
∵8×8的正方形的面积为64,
而长为13、宽为5的长方形的面积为65,
∴这4块纸片不能拼成一个长为13、宽为5的长方形.
02
知识精讲
2000多年前,古希腊数学家欧几里得对前人在数学上的成果进行了系统整理,他把人们公认的一些真命题作为公理,并以此为出发点,用推理的方法证实了一系列命题,编纂成了人类文明史上具有里程碑意义的数学巨著——《原本》.
这学期,我们也曾把一些真命题作为基本事实,并从基本事实出发证实了有关余角、补角、对顶角、平行线的一些结论.
02
知识精讲
【证明与定理】
根据已知的真命题,确定某个命题真实性的过程叫做证明.
经过证明的真命题称为定理.
证明与定理
02
知识精讲
【探究1】填空完成推理过程:如图:已知∠CGD=∠CAB,∠ADE+∠CEF=180°,求证:∠1=∠2.
证明:∵∠ADE+∠CEF=180°(__________________________);
∴EF∥AD(__________________________);
∴∠2=∠3(__________________________);
∵∠CGD=∠CAB(__________________________);
∴DG∥AB(__________________________);
∴∠1=∠3(__________________________);
∵∠2=∠3(__________________________);
∴∠1=∠2(__________________________).
已知
同旁内角互补,两直线平行
两直线平行,同位角相等
已知
同位角相等,两直线平行
两直线平行,内错角相等
等量代换
已证
等量代换:
一个量用与它相等的量代替
02
知识精讲
证明过程通常包含几个推理,每个推理应包括因、果和由因得果的依据.
其中,(1)“因”是已知事项;
(2)“果”是推得的结论;
(3)“由因得果的依据”是基本事实、定义、已学过的定理以及等式性质、不等式性质等.
证明过程必须做到言必有据~
02
知识精讲
【公理(九个基本事实)】
(1)两点确定一条直线;
(2)两点之间,线段最短;
(3)过一点有且只有一条直线与这条直线垂直;
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线平行;
(5)过直线外一点有且只有一条直线与这条直线平行;
(6)全等三角形的对应边、对应角分别相等;
(7)边边公理(SSS)有三边对应相等的两个三角形全等;
(8)两直线平行,同位角相等;
(9)不共线三点确定一个圆.
公理(基本事实)
02
知识精讲
为了使证明过程表达得更加简明,前面推理所得的“果”作为下一个推理的“因”,通常可以省略不写.
eg: ∴∠2=∠3(两直线平行,同位角相等);
∵∠CGD=∠CAB(已知);
∴DG∥AB(同位角相等,两直线平行);
∴∠1=∠3(两直线平行,内错角相等);
∵∠2=∠3(已证);
∴∠1=∠2(等量代换).
前面已证,这边可省略
02
知识精讲
【证明与图形有关的命题,一般有以下步骤】
(1)根据题意,画出图形;
(2)根据命题的条件、结论,结合图形,写出已知、求证;
(3)写出证明过程.
证明的一般步骤
02
知识精讲
【探究2】证明:三角形的内角和定理(三角形三个内角的和等于180°).
已知:ABC.
求证:∠A+∠B+∠C=180°.
B
C
A
(1)根据题意,画出图形
(2)根据命题的条件、结论,结合图形,写出已知、求证
02
知识精讲
证明:如图,画ABC的边BC的延长线CD,过点C画CE // AB.
B
C
A
(3)写出证明过程
D
E
2
1
这样的辅助线是从拼图得到的启发
02
知识精讲
∵CE // AB(辅助线画法),
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠A(两直线平行,内错角相等).
∵∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
(3)写出证明过程
证明:如图,画ABC的边BC的延长线CD,过点C画CE // AB.
B
C
A
D
E
2
1
02
知识精讲
【探究3】三角形的一个外角和与它不相邻的两个内角有怎样的数量关系?
已知:ABC中,∠A+∠B+∠ACB=180°.
求证:∠ACD=∠A+∠B.
(1)根据题意,画出图形
(2)根据命题的条件、结论,结合图形,写出已知、求证
B
C
A
D
02
知识精讲
证明:
∵∠A+∠B+∠ACB=180°(已知),
且∠ACD+∠ACB=180°(平角的定义),
∴∠ACB=∠A+∠B(等量代换).
(3)写出证明过程
B
C
A
D
02
知识精讲
由三角形内角和定理,可以推出:
三角形的外角等于与它不相邻的两个内角的和.
【定理的推论】
像这样,由一个定理直接推出的正确结论,叫做这个定理的推论,它和定理一样,可以作为进一步证明的依据.
定理的推论
例1、4个人进行游泳比赛,赛前A,B,C,D等4名选手进行预测,A说:“我肯定得第一名”,B说:“我绝对不会得最后一名”,C说:“我不可能得第一名,也不会得最后一名”,D说:“那只有我是最后一名!”,比赛揭晓后,发现他们之中只有一位预测错误,预测错误的人是________.
A
【推理】
【分析】
如果A错,则B为第一,C为第二,D为最后一名,所以A是错的;
如果B错,则B最后,D也错,出现矛盾;
如果C错,则C是第一或最后一名,与A第一、D最后,矛盾;
如果D错,其他都对的话,则没有最后一名.
例2、下列命题,不是基本事实的是( )
A.过平面上两点,有且只有一条直线
B.两点之间的连线中,线段最短
C.在等式两边同时加上(或减去)同一个整式,所得结果仍为等式
D.同角的补角相等
D
【公理(基本事实】
【分析】
D、同角的补角相等,是由等量代换推理得出的,是定理不是基本事实.
例3、如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:解:
∵∠3=∠4(已知)
∴AE∥______(________________________)
∴∠EDC=∠5(________________________)
∵∠5=∠A(已知)
∴∠EDC=______(等量代换)
∴DC∥AB(________________________)
∴∠5+∠ABC=180°(________________________),即∠5+∠2+∠3=180°
∵∠1=∠2(已知)
∴∠5+∠1+∠3=180°(________________________),即∠BCF+∠3=180°
∴BE∥CF(________________________).
【证明】
BC
内错角相等,两直线平行
∠A
两直线平行,内错角相等
同位角相等,两直线平行
两直线平行,同旁内角互补
等量代换
同旁内角互补,两直线平行
例4、数学中的两位数乘法藏着许多的运算规律,现请观察下列几个等式:
23×83=(2×8+3)×100+3×3=1909;
38×78=(3×7+8)×100+8×8=2964;
45×65=(4×6+5)×100+5×5=2925.
(1)请你类比上面的等式,计算:①84×24;②562;
(2)请你写出以上等式所体现一般的规律,并用所学知识证明.
(2)一般规律为:
(10a+c)×[10×(10-a)+c]=[a×(10-a)+c]×100+c×c,
证明如下:左边=10a×10×(10-a)+10a×c+c×10×(10-a)+c×c
=100a×(10-a)+10ac+10c×(10-a)+c×c
=100a×(10-a)+100c+c×c
=[a×(10-a)+c]×100+c×c=右边.
【分析】
(1)①84×24
=(8×2+4)×100+4×4=2016;
②562=56×56
=(5×5+6)×100+6×6=3100+36=3136;
例5、如图,ABC中,D,E,F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,请从以下给出三个条件①∠1+∠2=180°;②∠3=∠C;③DE∥BC再选取两个为条件,剩下的一个作为结论,并请完成证明.
条件(已知)________________________;结论(求证)__________.
【证明】
∵∠1是DEH的外角(已知),
∴∠1=∠3+∠4(外角的性质).
又∵∠1+∠2=180°(已知),
∴∠3+∠4+∠2=180°(等量代换),
∵∠3=∠C(已知),
∴∠C+∠4+∠2=180°(等量代换),即∠DEC+∠C=180°,
∴DE∥BC(同旁内角互补,两直线平行).
∠1+∠2=180°,∠3=∠C
DE∥BC
课后总结
【证明与定理】
根据已知的真命题,确定某个命题真实性的过程叫做证明.
经过证明的真命题称为定理.
【公理(九个基本事实)】
(1)两点确定一条直线;
(2)两点之间,线段最短;
(3)过一点有且只有一条直线与这条直线垂直;
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线平行;
(5)过直线外一点有且只有一条直线与这条直线平行;
(6)全等三角形的对应边、对应角分别相等;
(7)边边公理(SSS)有三边对应相等的两个三角形全等;
(8)两直线平行,同位角相等;
(9)不共线三点确定一个圆.
课后总结
【证明与图形有关的命题,一般有以下步骤】
(1)根据题意,画出图形;
(2)根据命题的条件、结论,结合图形,写出已知、求证;
(3)写出证明过程.
【定理的推论】
由一个定理直接推出的正确结论,叫做这个定理的推论,它和定理一样,可以作为进一步证明的依据.
谢谢学习
Thank you for learning
12.2 证明
Proof
苏科版七年级下册第12章证明
教学目标
01
了解证明、定理与定理的推论的含义,认识九个基本事实
02
掌握证明的一般步骤与书写规范
知识精讲
情境引入
01
视觉误差~
是静的,还是动的?
知识精讲
情境引入
01
视觉误差~
左右两边处于中心位置的圆大小是否相等?
知识精讲
情境引入
01
观察、操作、实验是人们认识事物的重要手段,通过观察、操作、实验,常常可以探索发现一些结论,但是这些结论不一定正确,数学中,探索发现的结论需要加以证实.
知识精讲
情境引入
01
Q1:如图,两条线段AB与CD哪一条长一些?
通过度量线段AB、CD的长度,可以证实:线段CD比线段AB长,故以上结论不正确.
看上去线段AB比线段CD长
But
C B D
A
知识精讲
情境引入
01
Q2:把图(1)长方形草坪中间1m宽的直道,改成图(2)中处处1m宽的“曲径”,这两条小道的面积相等吗?
1m
1m
图(1) 图(2)
看上去不相等,但其实相等
知识精讲
情境引入
01
【分析】
如果将图(2)中小道左边的草坪向右平移1m,并将其与右边的草坪拼在一起,那么得到一个长为(a-1)m、宽为bm的长方形.
于是,“曲径”的面积,
即“原长方形的面积”-“现长方形的面积
=ab-b(a-1)=ab-ab+b=b(m );
而“直道”的面积=1×b=b(m );
1m
图(2)
∴通过图形的平移与计算可得:
两条小道的面积相等.
知识精讲
情境引入
01
Q3:当x=-5、-0.5、0、2、3时,分别计算代数式x -2x+2的值,你发现了什么?
x取不同的值,
x -2x+2的值都是正数
x x -2x+2
-5 37
-0.5 3.25
0 2
2 2
3 5
知识精讲
情境引入
01
【分析】
x -2x+2=(x -2x+1)+1=(x-1) +1,
∵(x-1) ≥0,
∴(x-1) +1≥1.
∴通过将x -2x+2变形为(x-1) +1可证:
不管x取何值,代数式的值都不小于1.
知识精讲
情境引入
01
Q4:图(1)是一张8×8的正方形纸片,把它剪成4块,按图(2)重新拼合.
这4块纸片恰好能拼成一个长为13、宽为5的长方形吗?
看上去能,但其实不能,图(2)本身就画得不对
知识精讲
情境引入
01
【分析】
∵8×8的正方形的面积为64,
而长为13、宽为5的长方形的面积为65,
∴这4块纸片不能拼成一个长为13、宽为5的长方形.
02
知识精讲
2000多年前,古希腊数学家欧几里得对前人在数学上的成果进行了系统整理,他把人们公认的一些真命题作为公理,并以此为出发点,用推理的方法证实了一系列命题,编纂成了人类文明史上具有里程碑意义的数学巨著——《原本》.
这学期,我们也曾把一些真命题作为基本事实,并从基本事实出发证实了有关余角、补角、对顶角、平行线的一些结论.
02
知识精讲
【证明与定理】
根据已知的真命题,确定某个命题真实性的过程叫做证明.
经过证明的真命题称为定理.
证明与定理
02
知识精讲
【探究1】填空完成推理过程:如图:已知∠CGD=∠CAB,∠ADE+∠CEF=180°,求证:∠1=∠2.
证明:∵∠ADE+∠CEF=180°(__________________________);
∴EF∥AD(__________________________);
∴∠2=∠3(__________________________);
∵∠CGD=∠CAB(__________________________);
∴DG∥AB(__________________________);
∴∠1=∠3(__________________________);
∵∠2=∠3(__________________________);
∴∠1=∠2(__________________________).
已知
同旁内角互补,两直线平行
两直线平行,同位角相等
已知
同位角相等,两直线平行
两直线平行,内错角相等
等量代换
已证
等量代换:
一个量用与它相等的量代替
02
知识精讲
证明过程通常包含几个推理,每个推理应包括因、果和由因得果的依据.
其中,(1)“因”是已知事项;
(2)“果”是推得的结论;
(3)“由因得果的依据”是基本事实、定义、已学过的定理以及等式性质、不等式性质等.
证明过程必须做到言必有据~
02
知识精讲
【公理(九个基本事实)】
(1)两点确定一条直线;
(2)两点之间,线段最短;
(3)过一点有且只有一条直线与这条直线垂直;
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线平行;
(5)过直线外一点有且只有一条直线与这条直线平行;
(6)全等三角形的对应边、对应角分别相等;
(7)边边公理(SSS)有三边对应相等的两个三角形全等;
(8)两直线平行,同位角相等;
(9)不共线三点确定一个圆.
公理(基本事实)
02
知识精讲
为了使证明过程表达得更加简明,前面推理所得的“果”作为下一个推理的“因”,通常可以省略不写.
eg: ∴∠2=∠3(两直线平行,同位角相等);
∵∠CGD=∠CAB(已知);
∴DG∥AB(同位角相等,两直线平行);
∴∠1=∠3(两直线平行,内错角相等);
∵∠2=∠3(已证);
∴∠1=∠2(等量代换).
前面已证,这边可省略
02
知识精讲
【证明与图形有关的命题,一般有以下步骤】
(1)根据题意,画出图形;
(2)根据命题的条件、结论,结合图形,写出已知、求证;
(3)写出证明过程.
证明的一般步骤
02
知识精讲
【探究2】证明:三角形的内角和定理(三角形三个内角的和等于180°).
已知:ABC.
求证:∠A+∠B+∠C=180°.
B
C
A
(1)根据题意,画出图形
(2)根据命题的条件、结论,结合图形,写出已知、求证
02
知识精讲
证明:如图,画ABC的边BC的延长线CD,过点C画CE // AB.
B
C
A
(3)写出证明过程
D
E
2
1
这样的辅助线是从拼图得到的启发
02
知识精讲
∵CE // AB(辅助线画法),
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠A(两直线平行,内错角相等).
∵∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
(3)写出证明过程
证明:如图,画ABC的边BC的延长线CD,过点C画CE // AB.
B
C
A
D
E
2
1
02
知识精讲
【探究3】三角形的一个外角和与它不相邻的两个内角有怎样的数量关系?
已知:ABC中,∠A+∠B+∠ACB=180°.
求证:∠ACD=∠A+∠B.
(1)根据题意,画出图形
(2)根据命题的条件、结论,结合图形,写出已知、求证
B
C
A
D
02
知识精讲
证明:
∵∠A+∠B+∠ACB=180°(已知),
且∠ACD+∠ACB=180°(平角的定义),
∴∠ACB=∠A+∠B(等量代换).
(3)写出证明过程
B
C
A
D
02
知识精讲
由三角形内角和定理,可以推出:
三角形的外角等于与它不相邻的两个内角的和.
【定理的推论】
像这样,由一个定理直接推出的正确结论,叫做这个定理的推论,它和定理一样,可以作为进一步证明的依据.
定理的推论
例1、4个人进行游泳比赛,赛前A,B,C,D等4名选手进行预测,A说:“我肯定得第一名”,B说:“我绝对不会得最后一名”,C说:“我不可能得第一名,也不会得最后一名”,D说:“那只有我是最后一名!”,比赛揭晓后,发现他们之中只有一位预测错误,预测错误的人是________.
A
【推理】
【分析】
如果A错,则B为第一,C为第二,D为最后一名,所以A是错的;
如果B错,则B最后,D也错,出现矛盾;
如果C错,则C是第一或最后一名,与A第一、D最后,矛盾;
如果D错,其他都对的话,则没有最后一名.
例2、下列命题,不是基本事实的是( )
A.过平面上两点,有且只有一条直线
B.两点之间的连线中,线段最短
C.在等式两边同时加上(或减去)同一个整式,所得结果仍为等式
D.同角的补角相等
D
【公理(基本事实】
【分析】
D、同角的补角相等,是由等量代换推理得出的,是定理不是基本事实.
例3、如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:解:
∵∠3=∠4(已知)
∴AE∥______(________________________)
∴∠EDC=∠5(________________________)
∵∠5=∠A(已知)
∴∠EDC=______(等量代换)
∴DC∥AB(________________________)
∴∠5+∠ABC=180°(________________________),即∠5+∠2+∠3=180°
∵∠1=∠2(已知)
∴∠5+∠1+∠3=180°(________________________),即∠BCF+∠3=180°
∴BE∥CF(________________________).
【证明】
BC
内错角相等,两直线平行
∠A
两直线平行,内错角相等
同位角相等,两直线平行
两直线平行,同旁内角互补
等量代换
同旁内角互补,两直线平行
例4、数学中的两位数乘法藏着许多的运算规律,现请观察下列几个等式:
23×83=(2×8+3)×100+3×3=1909;
38×78=(3×7+8)×100+8×8=2964;
45×65=(4×6+5)×100+5×5=2925.
(1)请你类比上面的等式,计算:①84×24;②562;
(2)请你写出以上等式所体现一般的规律,并用所学知识证明.
(2)一般规律为:
(10a+c)×[10×(10-a)+c]=[a×(10-a)+c]×100+c×c,
证明如下:左边=10a×10×(10-a)+10a×c+c×10×(10-a)+c×c
=100a×(10-a)+10ac+10c×(10-a)+c×c
=100a×(10-a)+100c+c×c
=[a×(10-a)+c]×100+c×c=右边.
【分析】
(1)①84×24
=(8×2+4)×100+4×4=2016;
②562=56×56
=(5×5+6)×100+6×6=3100+36=3136;
例5、如图,ABC中,D,E,F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,请从以下给出三个条件①∠1+∠2=180°;②∠3=∠C;③DE∥BC再选取两个为条件,剩下的一个作为结论,并请完成证明.
条件(已知)________________________;结论(求证)__________.
【证明】
∵∠1是DEH的外角(已知),
∴∠1=∠3+∠4(外角的性质).
又∵∠1+∠2=180°(已知),
∴∠3+∠4+∠2=180°(等量代换),
∵∠3=∠C(已知),
∴∠C+∠4+∠2=180°(等量代换),即∠DEC+∠C=180°,
∴DE∥BC(同旁内角互补,两直线平行).
∠1+∠2=180°,∠3=∠C
DE∥BC
课后总结
【证明与定理】
根据已知的真命题,确定某个命题真实性的过程叫做证明.
经过证明的真命题称为定理.
【公理(九个基本事实)】
(1)两点确定一条直线;
(2)两点之间,线段最短;
(3)过一点有且只有一条直线与这条直线垂直;
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线平行;
(5)过直线外一点有且只有一条直线与这条直线平行;
(6)全等三角形的对应边、对应角分别相等;
(7)边边公理(SSS)有三边对应相等的两个三角形全等;
(8)两直线平行,同位角相等;
(9)不共线三点确定一个圆.
课后总结
【证明与图形有关的命题,一般有以下步骤】
(1)根据题意,画出图形;
(2)根据命题的条件、结论,结合图形,写出已知、求证;
(3)写出证明过程.
【定理的推论】
由一个定理直接推出的正确结论,叫做这个定理的推论,它和定理一样,可以作为进一步证明的依据.
谢谢学习
Thank you for learning
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
