第十九章 一次函数 章节复习课件(共83张PPT)
文档属性
| 名称 | 第十九章 一次函数 章节复习课件(共83张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 06:44:51 | ||
图片预览









文档简介
(共83张PPT)
一次函数章节复习
1.回顾总结本章的知识点和知识结构;
2.一次函数的定义、图象和性质的应用; (重点)
3.运用函数思想解决实际问题;(难点)
4.总结本章重要思想方法.
一、函数
1.变量和常量:
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
2.函数:
一般地,在一个变化过程中,如果有两个变量 x 与 y ,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x = a 时 y = b,那么 b 叫做当自变量的值为 a 时的函数值.
一、函数
3.函数的图象:
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
如下图的曲线即函数S=x2 (x>0)的图象.
4.描点法画函数图象的一般步骤:
第一步:列表---表中给出一些自变量的值及其对应的函数值;
第二步:描点---在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步:连线---按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
一、函数
5.三种表示函数的方法优缺点以及它们之间的联系:
一、函数
二、一次函数
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
注:(1)k是常数,且k≠0; (2)自变量x的次数是1;
(3)自变量x的取值范围是一切实数;(4)y=kx,则称y与x成正比例;反之,若y与x成正比例,则可设y=kx.
1.正比例函数:
二、一次函数
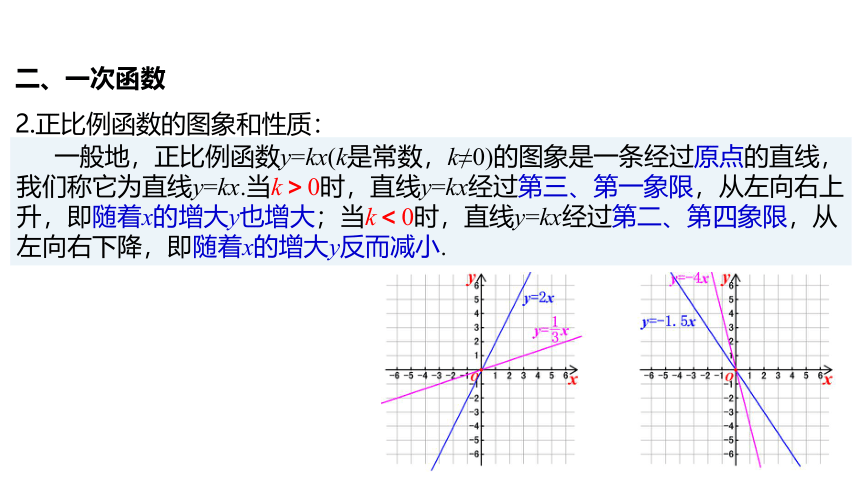
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小.
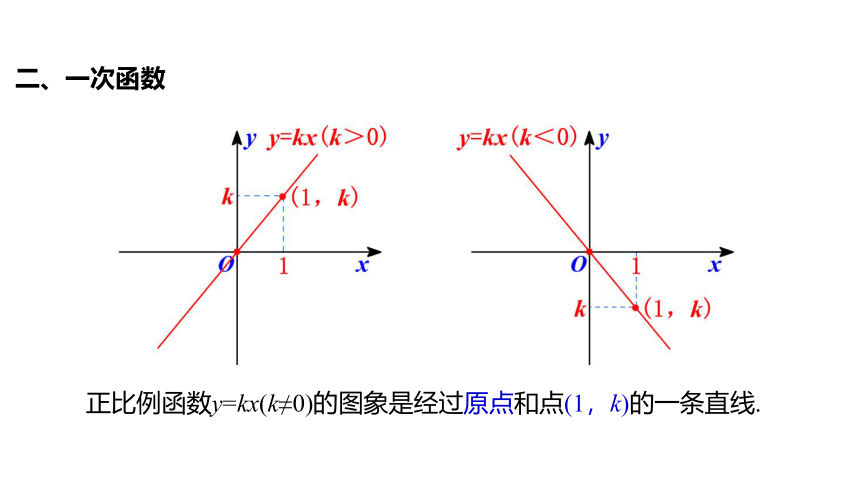
2.正比例函数的图象和性质:
正比例函数y=kx(k≠0)的图象是经过原点和点(1,k)的一条直线.
二、一次函数
二、一次函数
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
特别注意:k≠0,自变量x的指数是1.
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数.
3.一次函数的概念:
二、一次函数
4.一次函数的图象的平移规律:
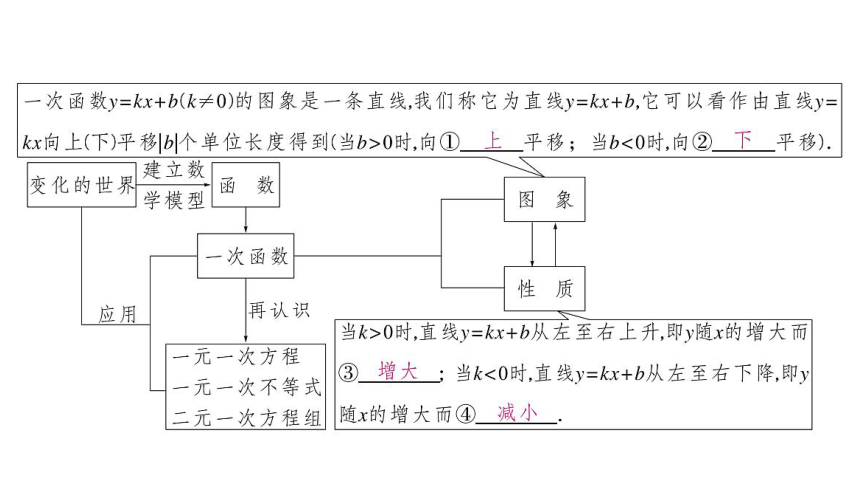
一次函数y=kx+b(k≠0)的图象也是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx向上(或向下)平移|b|个单位长度而得到的.
当b>0时,向上平移;
当b<0时,向下平移.
画一次函数的图象采用两点法一般选取与x轴的交点(-,0)与y轴的交点(0,b).
二、一次函数
5.一次函数的图象和性质:
三、用待定系数法求一次函数的解析式
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
三、用待定系数法求一次函数的解析式
用待定系数法求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.
四、一次函数与方程、不等式
1.一次函数与一元一次方程的关系
四、一次函数与方程、不等式
2.一次函数与一元一次不等式的关系
四、一次函数与方程、不等式
3.一次函数与二元一次方程组的关系
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
从“数”的角度看,解这样的方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看,解这样的方程组,相当于确定两条相应直线交点的坐标. 因此,我们可以用画一次函数图象的方法得到方程组的解.
五、一次函数的实际应用
01
函数的有关概念及图象
例1.当m,n为何值时,是关于x的一次函数?当m,n为何值时,y是关于x的正比例函数?
解:若y=(5m-3)x2-n+(m+n)是关于x的一次函数,
则有
解得
所以当m≠且n=1时,y=(5m-3)x2-n+(m+n)是关于x的一次函数.
例2.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
C
例3.如图,平面直角坐标系中,在边长为1的正方形ABCD的边上有一动点P沿A→B→C→D→A运动一周,则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
D
【1-1】根据图中的程序,当输入数值x为-2时,输出数值y为______.
6
【1-2】小亮从家去学校,为了锻炼身体,一开始跑步前进,跑累了再步行走完余下的路程,下图中,纵轴表示离家的距离,横轴表示出发后的时间,则下列四个图象中较符合该学生走法的是( )
C
【1-3】小明同学骑自行车去郊外春游,如图表示他
离家的距离y(km)与所用的时间x(h)之间关系的函数
图象.
(1)根据图象回答:小明到达离家最远的
地方需______h;
(2)小明出发2.5 h后离家_______km;
(3)小明出发__________h后离家12 km.
3
22.5
2.5
12
0.8或5.2
02
正比例函数的图象与性质
例4.已知正比例函数y=(2m+4)x.求:
(1)m为何值时,函数图象经过第一、三象限;
(2)m为何值时,y随x的增大而减小;
(3)m为何值时,点(1,3)在该函数的图象上.
解:∵点(1,3)在该函数的图象上,∴2m+4=3,解得m=-.
解:∵函数图象经过第一、三象限,
∴2m+4>0,解得m>-2.
解:∵y随x的增大而减小,
∴2m+4<0,解得m<-2.
例5.若正比例函数y=(m﹣2)x的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是( )
A.m>0 B.m<0 C.m>2 D.m<2
【解析】根据题意,知:y随x的增大而减小,
则k<0,即m﹣2<0,m<2.
故选:D.
D
例6.如图,正比例函数y=kx的图象经过点A,点A在第四象限,且横坐标为3.过点A作AH⊥x轴,垂足为点H,且△AOH的面积为3.
(1)求正比例函数的解析式;
解: (1)∵点A在第四象限,点A的横坐标为3,且△AOH的面积为3
∴点A的纵坐标为-2
∴点A的坐标为(3,-2)
将点A(3,-2)代入y=kx
得-2=3k,解得k=-
∴正比例函数的解析式为y=-x.
(2)在x轴上是否存在一点P,使△AOP的面积为5 若存在,求出点P的坐标;若不存在,请说明理由.
解: (2)存在.
设点P的坐标为(a, 0)则S△AOP=|a|×|-2|=5,
解得a=±5
∴在x轴上存在点P,使△AOP的面积为5,点P的坐标为(-5,0)或(5,0)
【2-1】已知正比例函数y= (3k-1)x,若y随x的增大而增大,则k的取值范围是( )
A.k<0 B.k>0 C. k< D. k>
【2-2】已知正比例函数y=(1-2m)x的图象过第二,第四象限,则m的取值范围是( )
A. m< B.m> C. m>0 D. m<0
D
B
【2-3】若点,在正比例函数的图象上,且时,则m的值可以是( )
A.2 B.0 C. D.
【解析】∵点,在正比例函数的图象上,且时,
∴y随x的增大而减小,
∴,
故选:D.
D
【2-4】已知正比例函数图像经过点,求:
(1)这个函数的解析式;
(2)判断点是否在这个函数图像上;
(3)图像上两点,,如果,比较,的大小.
(1)解:正比例函数的图象经过点,
时,
解得
这个函数的解析式为;
【2-4】已知正比例函数图像经过点,求:
(1)这个函数的解析式;
(2)判断点是否在这个函数图像上;
(3)图像上两点,,如果,比较,的大小.
(2)解:将代入中得:,
点不在这个函数图象上;
(3)解: ,
随x的增大而减小,
又
.
03
一次函数的图象与性质
例7.已知一次函数,随的增大而减小,且与轴的交点在轴的正半轴上,则的取值范围是( )
A. B. C. D.以上都不对
【详解】解:∵一次函数,随的增大而减小,且与轴的交点在轴的正半轴上,
∴,
解得.
故选:.
C
例8.已知关于x的一次函数的图象上两点,,若时,,则m的取值范围是( )
A. B. C. D.
【分析】∵当时,,
∴y随x的增大而减小,
∴,
∴.
故选:C.
C
例9.已知一次函数的图象不经过第二象限,则的范围_________________.
【分析】解:∵一次函数的图象不经过第二象限,
①图象经过第一,三,四象限,
∴,解得
①图象经过第一,三象限,
∴,解得,
故答案为:.
例10.如图,正方形A1B1C1O, A2B2C2C1,A3B3C3C2, ...按其所示放置,点A1,A2,A3,…和C1,C2, C3,…分别在直线y=x+1和x轴上,则点B2025的横坐标是___________.
【分析】当x=0时,y=x+1=1,
∴A1(0,1),B1(1,1)
易得每一个正方形的边长都是它前一个正方形边长的2倍,因此B2的横坐标为1+1×2=1+2=3=22-1,B3的横坐标为1+1×2+2×2=1+2+4=7=23-1,B4的横坐标为24-1,…,B2025的横坐标为22025-1.
22025-1
【3-1】已知点,,三点在直线的图像上,且,则,,的大小关系为( )
A. B. C. D.
【3-2】已知,是关于x的函数图象上的两点,当时,,则m的取值范围是( )
A. B. C. D.
B
C
【3-3】已知一次函数y=2x-4.
(1)画出它的图象;
(2)写出函数图象与x轴、y轴交点的坐标;
(3)求这条直线与两坐标轴所围成的三角形面积.
解:(1)如右图;
(2)与x轴、y轴交点坐标分别是A(2,0)、B(0,-4);(3) A(2,0)、B(0,-4)
∴OA=2,OB=4
∴S△OAB=×2×4=4.
【3-4】已知一次函数y=ax-a+1 (a为常数,且a≠0).
(1)若点(-,3)在该函数的图象上,求a的值;
(2)若当-1≤x≤2时,函数有最大值2,求a的值.
解: (1)把(-,3)代入y=ax-a+1,得-a-a+l=3,解得a=-
(2)①当a>0时,y随x的增大而增大,则当x=2时,y最大=2,把(2,2)代入函数解析式得2=2a-a+1,解得a=1;
②当a<0时,y随x的增大而减小,则当x=-1时, y最大=2,把(-1,2)代入函数解析式得2=-a-a+1,解得a=-0. 5.
综上,a=1或a=-0. 5.
04
一次函数的“图象共存”问题
例11.一次函数与正比例函数的图象在同一坐标系中不可能是( )
B
两个一次函数y1=ax+b和y2=bx+a (a≠b)在同一直角坐标系中的图象可能是( )
A
05
待定系数法求一次函数解析式
例12.若一次函数的图象经过点A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
∵一次函数的图象与直线y=-x+3平行
∴k=-1
把A(2,0)代入y=-x+b中
解得b=2
∴一次函数的解析式为y=-x+2.
例13.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
解:①当k>0时,y随x的增大而增大
∴当x=-3时,y=-5,当x=6时,y=-2.
把这两组值分别代入y=kx+b中
解方程组得
∴一次函数的解析式为y=x-4.
解:②当k<0时,y随x的增大而减小
当x=-3时,y=-2,当x=6时,y=-5
把这两组值分别代入y=kx+b中
得到 解方程组得
∴一次函数的解析式为y=-x-3
综上所述,一次函数的解析式为y=x-4或y=-x-3
例13.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
例14.如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且点B的横坐标为1,求直线l对应的函数解析式.
解:设直线l对应的函数解析式为y=kx+b
把x=1代入y=2x, 得y=2
则点B坐标为(1,2)
把(1,2),(0,3)代入y=kx+b
得到 解方程组得
所以直线l对应的函数解析式为y=-x+3
【5-1】一次函数y=mx+|m-1|的图象经过点(0,2),且y随x的增大而增大,则m的值是_____.
【5-2】已知一次函数y=kx+3的图象与坐标轴围成的三角形的面积是1.5,则此一次函数的解析式可能为__________________.
3
y=3x+3或y=-3x+3
【5-3】已知一次函数的图象经过点(9,0)和点(24,20),写出函数的解析式.
解:设这个一次函数的解析式为y=kx+b
∵ y=kx+b的图象过点(9,0)与(24,20)
∴
解方程组得
∴ 这个一次函数的解析式为y=x-12.
06
一次函数的平移规律(上、下平移)
例15.在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
A. B.4 C. D.1
【分析】解:将一次函数的图象向左平移3个单位后,得到,
把代入,得到:,
解得.
故选:A.
A
【6-1】将直线向右平移2个单位后所得图象对应的函数表达式为( )
A. B. C. D.
【6-2】在平面直角坐标系中,将直线:平移后得到直线:,则下列平移作法中,正确的是( )
A.将直线向上平移6个单位 B.将直线向上平移3个单位
C.将直线向上平移2个单位 D.将直线向上平移4个单位
D
A
【6-3】直线y=6x-5向上平移3个单位,则平移后的直线与y轴的交点坐标是_______.
(0,-2)
07
一次函数与方程、不等式
例16.如图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),点B(2,0),则的解集为( )
A.-4<x<2
B.x<-4
C.x>2
D.x<-4或x>2
A
例17.如图,直线相交于点A,与x轴的交点坐标为,与y轴的交点坐标为.
(1)求出直线表示的一次函数关系式;
(2)当x分别取何值时,表示的两个一次
函数值分别大于0?
(3)当x取何值时,表示的函数值比的函数
值大?
(1)解:设直线的函数关系式为,
将点,代入,得,
解得,
∴直线的函数关系式为;
设直线的函数关系式为,
将,代入,得,
解得,
∴直线的函数关系式为
(2)解:由图可知,当时,,即直线的函数值大于0;
令,由得,
∴当时,,即直线的函数值大于0.
(3)解:由图可知,当时,表示的函数
值比的函数值大.
【7-1】直线l1: y=k1x+b与直线l2: y=k2x在同一平面直角坐标系中的图象如图所示,则关于x、y的方程组的解为________.
【7-2】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1是( )
A.0 B.1 C.2 D.3
【7-3】如图,函数y1=和y2=x+的图象相交于(-1,1),
(2,2)两点.当y1>y2时,x的取值范围是( )
A.x<-1 B.-1C.x>2 D.x<-1或x>2
D
B
【7-4】如图,已知直线y=kx+b经过点B(1,4),且与直线y=-x-11平行,与直线y=2x- 4交于点C,与x轴交于点A. 求直线AB的解析式及点C的坐标.
解:直线y=kx+b与直线y= -x-11平行
∴k=-1
∵直线y=-x+b经过点B(1,4)
∴-1+b=4, 解得b=5
∴直线AB的解析式为y=-x+5
联立方程组,解得
∴点C(3,2)
08
一次函数的实际应用
例18.某校手工社团计划制作A、B两类手工产品共个,准备在“红领巾爱心义卖”活动中出售,所获收入全部捐给希望小学建图书角. 若售出3个A类产品和2个B类产品收入元,售出4个A类产品和3个B类产品收入元.
(1)求A、B两类手工产品的售价各是多少元;
(1)解:设A类手工产品的售价是x元,B两类手工产品的售价是y元,
由题意得,
解得 ,
答:A类手工产品的售价是元,B类手工产品的售价是元.
(2)已知A类产品个数不超过B类产品的3倍,则制作A、B类两种产品各多少个的时候总收入最多?请说明理由.
(2)制作A类产品个B类产品个,获得总收入最多理由如下:
设总收入为W元,制作A类产品a个,则制作B类产品个,
类产品个数不超过B类产品的3倍,
,
解得:,
根据题意得:,
,
随着a的增大而增大,
当时,W取得最大值,最大值为(元),
此时,
答:制作A类产品个,B类产品个,获得总收入最多.
例19.为美化深圳市景,园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
解得
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值为
33×800+17×960=42720(元).
即最低成本是 42720 元.
例20.“人人冬奥,全民冰雪”,寒假赵凯一家乘车去离家千米的太白山滑雪场体验滑雪运动,出发后,前小时匀速行驶了千米,之后又匀速行驶了小时到达目的地,他们在滑雪场玩了小时后乘车回家他们离家的距离千米与时间小时之间的函数关系如图所示.
(1)求的函数表达式.
(2)赵凯一家经过多长时间离家的距离为千米?
(1)解:设段对应的解析式为:,把,,,代入,得,
,
解得:,
段对应的解析式为.
(2)由题意知,,,,,
设段对应的解析式为,把,,,代入,得,
,
解得:,
段对应的解析式为.
把代入,得,
解得,,
把代入,得,
解得,.
答:赵凯一家经过或小时,离家的距离为千米.
【8-1】某电器厂生产A、B两种家用小电器,若每天生产A、B两种电器共60件,这两种电器每件的成本和售价如表:
设每天生产A种电器x件,每天获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)如果该电器厂每天最多投入成本为4590元,那么每天生产多少件A种电器时,所获利润最大?并求出这个最大利润.
成本(元) 售价(元)
A种电器 85 105
B种电器 70 85
(1)解:由题意知,每天生产B种电器件,
∴,整理得,
∴y与x之间的函数关系式为 ;
(2)解:由题意得,,
解得,
∵,
∴随的增大而增大,
∴当时,有最大值,值为,
∴每天生产26件A种电器时,所获利润最大,最大利润为1030元.
【8-2】某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (1) y= (6100-5400)x+ (3900-3500) (30-x)
化简,得y=300x+12000
【8-2】某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (2) 10≤x≤12
(2)商场有哪几种进货方案可供选择
解: (2) 10≤x≤12
∵x为整数
∴x=10或11或12
∴商场有以下三种方案可供选择:
方案1:购空调10台,购彩电20台;
方案2:购空调11台,购彩电19台;
方案3:购空调12台,购彩电18台.
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (3)∵y=300x+12000 (10≤x≤12)
其中k=300>0. y随x的增大而增大
∴当x=12时,y有最大值,y最大=300×12+12000=15600元.
故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元.
09
一次函数与几何综合应用
例21.如图,在平面直角坐标系xoy中,直线y=- x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式.
(1)求AB的长和点C的坐标.
解:(1)∵直线y=-x+8与x轴,y轴分别交于点A,点B,
∴A(6,0),B(0,8),
在Rt△OAB中,∠AOB=90°,OA=6,OB=8,
∴AB==10,
∵△DAB沿直线AD折叠后的对应三角形为△DAC,
∴AC=AB=10,
∴OC=OA+AC=OA+AB=16,
∵点C在x轴的正半轴上,
∴点C的坐标为C(16,0).
(2)求直线CD的解析式.
(2)设点D的坐标为D(0,a)(a<0),
由题意可知CD=BD,CD2=BD2,
在Rt△OCD中,由勾股定理得162+y2=(8-y)2,
解得a=-12.
∴点D的坐标为D(0,-12),
可设直线CD的解析式为 y=kx-12(k≠0)
∵点C(16,0)在直线y=kx-12上,
∴16k-12=0,
解得k=,
∴直线CD的解析式为y= x-12.
【9-1】如图,在平面直角坐标系中,直线与轴交于点,与轴交于点.
(1)求直线的函数解析式;
(2)设点为线段上一点,当将的面积分为的两部分时,求点的坐标.
(1)解:设直线的函数解析式为,
点,点,
,
解得,
直线的函数解析式为;
(2)设点为线段上一点,当将的面积分为的两部分时,求点的坐标.
(2)解:点为线段上一点,
设点P的坐标为,
,
,
当时,,
解得:,
点P的坐标为,即;
当时,,
解得:,
点P的坐标为,即;
综上可知,当将的面积分为的两部分时,点的坐标为或.
【9-2】如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A,点B,点是直线上一动点(点P不与点A重合),点C的坐标为,O是坐标原点,设的面积为S.
(1)求S与x之间的函数关系式;
(2)当点P运动到什么位置时,的面积为15;
(3)过点P作的垂线与x轴、y轴分别交于点E,点F, 是
否存在这样的点P,使?若存在,求出
点P的坐标;若不存在,请说明理由.
解:(1)∵点是直线上一动点,
∴.
∵点C的坐标为,
∴,
当时,,
当时,;
综上所述,
(1)求S与x之间的函数关系式;
(2)当点P运动到什么位置时,的面积为15;
(2)解:令,
当时, ,
解得:,此时,,
当时,,
解得:,此时,;
综上所述,当点P运动到点或点时,的面积为15;
(3)过点P作的垂线与x轴、y轴分别交于点E,点F, 是否存在这样的点P,使?若存在,求出点P的坐标;若不存在,请说明理由.
(3)解:∵直线与x轴交于点A,与y轴交于点B,
∴,
∴,
∵,
∴,
当时,则直线的解析式为,
联立,解得:,
∴,此时点P与点A重合,不符合题意;
(3)过点P作的垂线与x轴、y轴分别交于点E,点F, 是否存在这样的点P,使?若存在,求出点P的坐标;若不存在,请说明理由.
当时,则直线的解析式为,
令,解得:,
∴.
综上所述,当时,点P 的坐标为.
一次函数章节复习
1.回顾总结本章的知识点和知识结构;
2.一次函数的定义、图象和性质的应用; (重点)
3.运用函数思想解决实际问题;(难点)
4.总结本章重要思想方法.
一、函数
1.变量和常量:
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
2.函数:
一般地,在一个变化过程中,如果有两个变量 x 与 y ,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x = a 时 y = b,那么 b 叫做当自变量的值为 a 时的函数值.
一、函数
3.函数的图象:
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
如下图的曲线即函数S=x2 (x>0)的图象.
4.描点法画函数图象的一般步骤:
第一步:列表---表中给出一些自变量的值及其对应的函数值;
第二步:描点---在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步:连线---按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
一、函数
5.三种表示函数的方法优缺点以及它们之间的联系:
一、函数
二、一次函数
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
注:(1)k是常数,且k≠0; (2)自变量x的次数是1;
(3)自变量x的取值范围是一切实数;(4)y=kx,则称y与x成正比例;反之,若y与x成正比例,则可设y=kx.
1.正比例函数:
二、一次函数
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小.
2.正比例函数的图象和性质:
正比例函数y=kx(k≠0)的图象是经过原点和点(1,k)的一条直线.
二、一次函数
二、一次函数
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
特别注意:k≠0,自变量x的指数是1.
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数.
3.一次函数的概念:
二、一次函数
4.一次函数的图象的平移规律:
一次函数y=kx+b(k≠0)的图象也是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx向上(或向下)平移|b|个单位长度而得到的.
当b>0时,向上平移;
当b<0时,向下平移.
画一次函数的图象采用两点法一般选取与x轴的交点(-,0)与y轴的交点(0,b).
二、一次函数
5.一次函数的图象和性质:
三、用待定系数法求一次函数的解析式
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
三、用待定系数法求一次函数的解析式
用待定系数法求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.
四、一次函数与方程、不等式
1.一次函数与一元一次方程的关系
四、一次函数与方程、不等式
2.一次函数与一元一次不等式的关系
四、一次函数与方程、不等式
3.一次函数与二元一次方程组的关系
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
从“数”的角度看,解这样的方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看,解这样的方程组,相当于确定两条相应直线交点的坐标. 因此,我们可以用画一次函数图象的方法得到方程组的解.
五、一次函数的实际应用
01
函数的有关概念及图象
例1.当m,n为何值时,是关于x的一次函数?当m,n为何值时,y是关于x的正比例函数?
解:若y=(5m-3)x2-n+(m+n)是关于x的一次函数,
则有
解得
所以当m≠且n=1时,y=(5m-3)x2-n+(m+n)是关于x的一次函数.
例2.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
C
例3.如图,平面直角坐标系中,在边长为1的正方形ABCD的边上有一动点P沿A→B→C→D→A运动一周,则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
D
【1-1】根据图中的程序,当输入数值x为-2时,输出数值y为______.
6
【1-2】小亮从家去学校,为了锻炼身体,一开始跑步前进,跑累了再步行走完余下的路程,下图中,纵轴表示离家的距离,横轴表示出发后的时间,则下列四个图象中较符合该学生走法的是( )
C
【1-3】小明同学骑自行车去郊外春游,如图表示他
离家的距离y(km)与所用的时间x(h)之间关系的函数
图象.
(1)根据图象回答:小明到达离家最远的
地方需______h;
(2)小明出发2.5 h后离家_______km;
(3)小明出发__________h后离家12 km.
3
22.5
2.5
12
0.8或5.2
02
正比例函数的图象与性质
例4.已知正比例函数y=(2m+4)x.求:
(1)m为何值时,函数图象经过第一、三象限;
(2)m为何值时,y随x的增大而减小;
(3)m为何值时,点(1,3)在该函数的图象上.
解:∵点(1,3)在该函数的图象上,∴2m+4=3,解得m=-.
解:∵函数图象经过第一、三象限,
∴2m+4>0,解得m>-2.
解:∵y随x的增大而减小,
∴2m+4<0,解得m<-2.
例5.若正比例函数y=(m﹣2)x的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是( )
A.m>0 B.m<0 C.m>2 D.m<2
【解析】根据题意,知:y随x的增大而减小,
则k<0,即m﹣2<0,m<2.
故选:D.
D
例6.如图,正比例函数y=kx的图象经过点A,点A在第四象限,且横坐标为3.过点A作AH⊥x轴,垂足为点H,且△AOH的面积为3.
(1)求正比例函数的解析式;
解: (1)∵点A在第四象限,点A的横坐标为3,且△AOH的面积为3
∴点A的纵坐标为-2
∴点A的坐标为(3,-2)
将点A(3,-2)代入y=kx
得-2=3k,解得k=-
∴正比例函数的解析式为y=-x.
(2)在x轴上是否存在一点P,使△AOP的面积为5 若存在,求出点P的坐标;若不存在,请说明理由.
解: (2)存在.
设点P的坐标为(a, 0)则S△AOP=|a|×|-2|=5,
解得a=±5
∴在x轴上存在点P,使△AOP的面积为5,点P的坐标为(-5,0)或(5,0)
【2-1】已知正比例函数y= (3k-1)x,若y随x的增大而增大,则k的取值范围是( )
A.k<0 B.k>0 C. k< D. k>
【2-2】已知正比例函数y=(1-2m)x的图象过第二,第四象限,则m的取值范围是( )
A. m< B.m> C. m>0 D. m<0
D
B
【2-3】若点,在正比例函数的图象上,且时,则m的值可以是( )
A.2 B.0 C. D.
【解析】∵点,在正比例函数的图象上,且时,
∴y随x的增大而减小,
∴,
故选:D.
D
【2-4】已知正比例函数图像经过点,求:
(1)这个函数的解析式;
(2)判断点是否在这个函数图像上;
(3)图像上两点,,如果,比较,的大小.
(1)解:正比例函数的图象经过点,
时,
解得
这个函数的解析式为;
【2-4】已知正比例函数图像经过点,求:
(1)这个函数的解析式;
(2)判断点是否在这个函数图像上;
(3)图像上两点,,如果,比较,的大小.
(2)解:将代入中得:,
点不在这个函数图象上;
(3)解: ,
随x的增大而减小,
又
.
03
一次函数的图象与性质
例7.已知一次函数,随的增大而减小,且与轴的交点在轴的正半轴上,则的取值范围是( )
A. B. C. D.以上都不对
【详解】解:∵一次函数,随的增大而减小,且与轴的交点在轴的正半轴上,
∴,
解得.
故选:.
C
例8.已知关于x的一次函数的图象上两点,,若时,,则m的取值范围是( )
A. B. C. D.
【分析】∵当时,,
∴y随x的增大而减小,
∴,
∴.
故选:C.
C
例9.已知一次函数的图象不经过第二象限,则的范围_________________.
【分析】解:∵一次函数的图象不经过第二象限,
①图象经过第一,三,四象限,
∴,解得
①图象经过第一,三象限,
∴,解得,
故答案为:.
例10.如图,正方形A1B1C1O, A2B2C2C1,A3B3C3C2, ...按其所示放置,点A1,A2,A3,…和C1,C2, C3,…分别在直线y=x+1和x轴上,则点B2025的横坐标是___________.
【分析】当x=0时,y=x+1=1,
∴A1(0,1),B1(1,1)
易得每一个正方形的边长都是它前一个正方形边长的2倍,因此B2的横坐标为1+1×2=1+2=3=22-1,B3的横坐标为1+1×2+2×2=1+2+4=7=23-1,B4的横坐标为24-1,…,B2025的横坐标为22025-1.
22025-1
【3-1】已知点,,三点在直线的图像上,且,则,,的大小关系为( )
A. B. C. D.
【3-2】已知,是关于x的函数图象上的两点,当时,,则m的取值范围是( )
A. B. C. D.
B
C
【3-3】已知一次函数y=2x-4.
(1)画出它的图象;
(2)写出函数图象与x轴、y轴交点的坐标;
(3)求这条直线与两坐标轴所围成的三角形面积.
解:(1)如右图;
(2)与x轴、y轴交点坐标分别是A(2,0)、B(0,-4);(3) A(2,0)、B(0,-4)
∴OA=2,OB=4
∴S△OAB=×2×4=4.
【3-4】已知一次函数y=ax-a+1 (a为常数,且a≠0).
(1)若点(-,3)在该函数的图象上,求a的值;
(2)若当-1≤x≤2时,函数有最大值2,求a的值.
解: (1)把(-,3)代入y=ax-a+1,得-a-a+l=3,解得a=-
(2)①当a>0时,y随x的增大而增大,则当x=2时,y最大=2,把(2,2)代入函数解析式得2=2a-a+1,解得a=1;
②当a<0时,y随x的增大而减小,则当x=-1时, y最大=2,把(-1,2)代入函数解析式得2=-a-a+1,解得a=-0. 5.
综上,a=1或a=-0. 5.
04
一次函数的“图象共存”问题
例11.一次函数与正比例函数的图象在同一坐标系中不可能是( )
B
两个一次函数y1=ax+b和y2=bx+a (a≠b)在同一直角坐标系中的图象可能是( )
A
05
待定系数法求一次函数解析式
例12.若一次函数的图象经过点A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
∵一次函数的图象与直线y=-x+3平行
∴k=-1
把A(2,0)代入y=-x+b中
解得b=2
∴一次函数的解析式为y=-x+2.
例13.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
解:①当k>0时,y随x的增大而增大
∴当x=-3时,y=-5,当x=6时,y=-2.
把这两组值分别代入y=kx+b中
解方程组得
∴一次函数的解析式为y=x-4.
解:②当k<0时,y随x的增大而减小
当x=-3时,y=-2,当x=6时,y=-5
把这两组值分别代入y=kx+b中
得到 解方程组得
∴一次函数的解析式为y=-x-3
综上所述,一次函数的解析式为y=x-4或y=-x-3
例13.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
例14.如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且点B的横坐标为1,求直线l对应的函数解析式.
解:设直线l对应的函数解析式为y=kx+b
把x=1代入y=2x, 得y=2
则点B坐标为(1,2)
把(1,2),(0,3)代入y=kx+b
得到 解方程组得
所以直线l对应的函数解析式为y=-x+3
【5-1】一次函数y=mx+|m-1|的图象经过点(0,2),且y随x的增大而增大,则m的值是_____.
【5-2】已知一次函数y=kx+3的图象与坐标轴围成的三角形的面积是1.5,则此一次函数的解析式可能为__________________.
3
y=3x+3或y=-3x+3
【5-3】已知一次函数的图象经过点(9,0)和点(24,20),写出函数的解析式.
解:设这个一次函数的解析式为y=kx+b
∵ y=kx+b的图象过点(9,0)与(24,20)
∴
解方程组得
∴ 这个一次函数的解析式为y=x-12.
06
一次函数的平移规律(上、下平移)
例15.在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
A. B.4 C. D.1
【分析】解:将一次函数的图象向左平移3个单位后,得到,
把代入,得到:,
解得.
故选:A.
A
【6-1】将直线向右平移2个单位后所得图象对应的函数表达式为( )
A. B. C. D.
【6-2】在平面直角坐标系中,将直线:平移后得到直线:,则下列平移作法中,正确的是( )
A.将直线向上平移6个单位 B.将直线向上平移3个单位
C.将直线向上平移2个单位 D.将直线向上平移4个单位
D
A
【6-3】直线y=6x-5向上平移3个单位,则平移后的直线与y轴的交点坐标是_______.
(0,-2)
07
一次函数与方程、不等式
例16.如图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),点B(2,0),则的解集为( )
A.-4<x<2
B.x<-4
C.x>2
D.x<-4或x>2
A
例17.如图,直线相交于点A,与x轴的交点坐标为,与y轴的交点坐标为.
(1)求出直线表示的一次函数关系式;
(2)当x分别取何值时,表示的两个一次
函数值分别大于0?
(3)当x取何值时,表示的函数值比的函数
值大?
(1)解:设直线的函数关系式为,
将点,代入,得,
解得,
∴直线的函数关系式为;
设直线的函数关系式为,
将,代入,得,
解得,
∴直线的函数关系式为
(2)解:由图可知,当时,,即直线的函数值大于0;
令,由得,
∴当时,,即直线的函数值大于0.
(3)解:由图可知,当时,表示的函数
值比的函数值大.
【7-1】直线l1: y=k1x+b与直线l2: y=k2x在同一平面直角坐标系中的图象如图所示,则关于x、y的方程组的解为________.
【7-2】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1
A.0 B.1 C.2 D.3
【7-3】如图,函数y1=和y2=x+的图象相交于(-1,1),
(2,2)两点.当y1>y2时,x的取值范围是( )
A.x<-1 B.-1
D
B
【7-4】如图,已知直线y=kx+b经过点B(1,4),且与直线y=-x-11平行,与直线y=2x- 4交于点C,与x轴交于点A. 求直线AB的解析式及点C的坐标.
解:直线y=kx+b与直线y= -x-11平行
∴k=-1
∵直线y=-x+b经过点B(1,4)
∴-1+b=4, 解得b=5
∴直线AB的解析式为y=-x+5
联立方程组,解得
∴点C(3,2)
08
一次函数的实际应用
例18.某校手工社团计划制作A、B两类手工产品共个,准备在“红领巾爱心义卖”活动中出售,所获收入全部捐给希望小学建图书角. 若售出3个A类产品和2个B类产品收入元,售出4个A类产品和3个B类产品收入元.
(1)求A、B两类手工产品的售价各是多少元;
(1)解:设A类手工产品的售价是x元,B两类手工产品的售价是y元,
由题意得,
解得 ,
答:A类手工产品的售价是元,B类手工产品的售价是元.
(2)已知A类产品个数不超过B类产品的3倍,则制作A、B类两种产品各多少个的时候总收入最多?请说明理由.
(2)制作A类产品个B类产品个,获得总收入最多理由如下:
设总收入为W元,制作A类产品a个,则制作B类产品个,
类产品个数不超过B类产品的3倍,
,
解得:,
根据题意得:,
,
随着a的增大而增大,
当时,W取得最大值,最大值为(元),
此时,
答:制作A类产品个,B类产品个,获得总收入最多.
例19.为美化深圳市景,园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
解得
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值为
33×800+17×960=42720(元).
即最低成本是 42720 元.
例20.“人人冬奥,全民冰雪”,寒假赵凯一家乘车去离家千米的太白山滑雪场体验滑雪运动,出发后,前小时匀速行驶了千米,之后又匀速行驶了小时到达目的地,他们在滑雪场玩了小时后乘车回家他们离家的距离千米与时间小时之间的函数关系如图所示.
(1)求的函数表达式.
(2)赵凯一家经过多长时间离家的距离为千米?
(1)解:设段对应的解析式为:,把,,,代入,得,
,
解得:,
段对应的解析式为.
(2)由题意知,,,,,
设段对应的解析式为,把,,,代入,得,
,
解得:,
段对应的解析式为.
把代入,得,
解得,,
把代入,得,
解得,.
答:赵凯一家经过或小时,离家的距离为千米.
【8-1】某电器厂生产A、B两种家用小电器,若每天生产A、B两种电器共60件,这两种电器每件的成本和售价如表:
设每天生产A种电器x件,每天获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)如果该电器厂每天最多投入成本为4590元,那么每天生产多少件A种电器时,所获利润最大?并求出这个最大利润.
成本(元) 售价(元)
A种电器 85 105
B种电器 70 85
(1)解:由题意知,每天生产B种电器件,
∴,整理得,
∴y与x之间的函数关系式为 ;
(2)解:由题意得,,
解得,
∵,
∴随的增大而增大,
∴当时,有最大值,值为,
∴每天生产26件A种电器时,所获利润最大,最大利润为1030元.
【8-2】某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (1) y= (6100-5400)x+ (3900-3500) (30-x)
化简,得y=300x+12000
【8-2】某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (2) 10≤x≤12
(2)商场有哪几种进货方案可供选择
解: (2) 10≤x≤12
∵x为整数
∴x=10或11或12
∴商场有以下三种方案可供选择:
方案1:购空调10台,购彩电20台;
方案2:购空调11台,购彩电19台;
方案3:购空调12台,购彩电18台.
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (3)∵y=300x+12000 (10≤x≤12)
其中k=300>0. y随x的增大而增大
∴当x=12时,y有最大值,y最大=300×12+12000=15600元.
故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元.
09
一次函数与几何综合应用
例21.如图,在平面直角坐标系xoy中,直线y=- x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式.
(1)求AB的长和点C的坐标.
解:(1)∵直线y=-x+8与x轴,y轴分别交于点A,点B,
∴A(6,0),B(0,8),
在Rt△OAB中,∠AOB=90°,OA=6,OB=8,
∴AB==10,
∵△DAB沿直线AD折叠后的对应三角形为△DAC,
∴AC=AB=10,
∴OC=OA+AC=OA+AB=16,
∵点C在x轴的正半轴上,
∴点C的坐标为C(16,0).
(2)求直线CD的解析式.
(2)设点D的坐标为D(0,a)(a<0),
由题意可知CD=BD,CD2=BD2,
在Rt△OCD中,由勾股定理得162+y2=(8-y)2,
解得a=-12.
∴点D的坐标为D(0,-12),
可设直线CD的解析式为 y=kx-12(k≠0)
∵点C(16,0)在直线y=kx-12上,
∴16k-12=0,
解得k=,
∴直线CD的解析式为y= x-12.
【9-1】如图,在平面直角坐标系中,直线与轴交于点,与轴交于点.
(1)求直线的函数解析式;
(2)设点为线段上一点,当将的面积分为的两部分时,求点的坐标.
(1)解:设直线的函数解析式为,
点,点,
,
解得,
直线的函数解析式为;
(2)设点为线段上一点,当将的面积分为的两部分时,求点的坐标.
(2)解:点为线段上一点,
设点P的坐标为,
,
,
当时,,
解得:,
点P的坐标为,即;
当时,,
解得:,
点P的坐标为,即;
综上可知,当将的面积分为的两部分时,点的坐标为或.
【9-2】如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A,点B,点是直线上一动点(点P不与点A重合),点C的坐标为,O是坐标原点,设的面积为S.
(1)求S与x之间的函数关系式;
(2)当点P运动到什么位置时,的面积为15;
(3)过点P作的垂线与x轴、y轴分别交于点E,点F, 是
否存在这样的点P,使?若存在,求出
点P的坐标;若不存在,请说明理由.
解:(1)∵点是直线上一动点,
∴.
∵点C的坐标为,
∴,
当时,,
当时,;
综上所述,
(1)求S与x之间的函数关系式;
(2)当点P运动到什么位置时,的面积为15;
(2)解:令,
当时, ,
解得:,此时,,
当时,,
解得:,此时,;
综上所述,当点P运动到点或点时,的面积为15;
(3)过点P作的垂线与x轴、y轴分别交于点E,点F, 是否存在这样的点P,使?若存在,求出点P的坐标;若不存在,请说明理由.
(3)解:∵直线与x轴交于点A,与y轴交于点B,
∴,
∴,
∵,
∴,
当时,则直线的解析式为,
联立,解得:,
∴,此时点P与点A重合,不符合题意;
(3)过点P作的垂线与x轴、y轴分别交于点E,点F, 是否存在这样的点P,使?若存在,求出点P的坐标;若不存在,请说明理由.
当时,则直线的解析式为,
令,解得:,
∴.
综上所述,当时,点P 的坐标为.
