《名师学典·数学》2014暑假人教数学七升八培训11.1.1三角形的高、中线和角平分线(典例解析+一课三练)
文档属性
| 名称 | 《名师学典·数学》2014暑假人教数学七升八培训11.1.1三角形的高、中线和角平分线(典例解析+一课三练) | 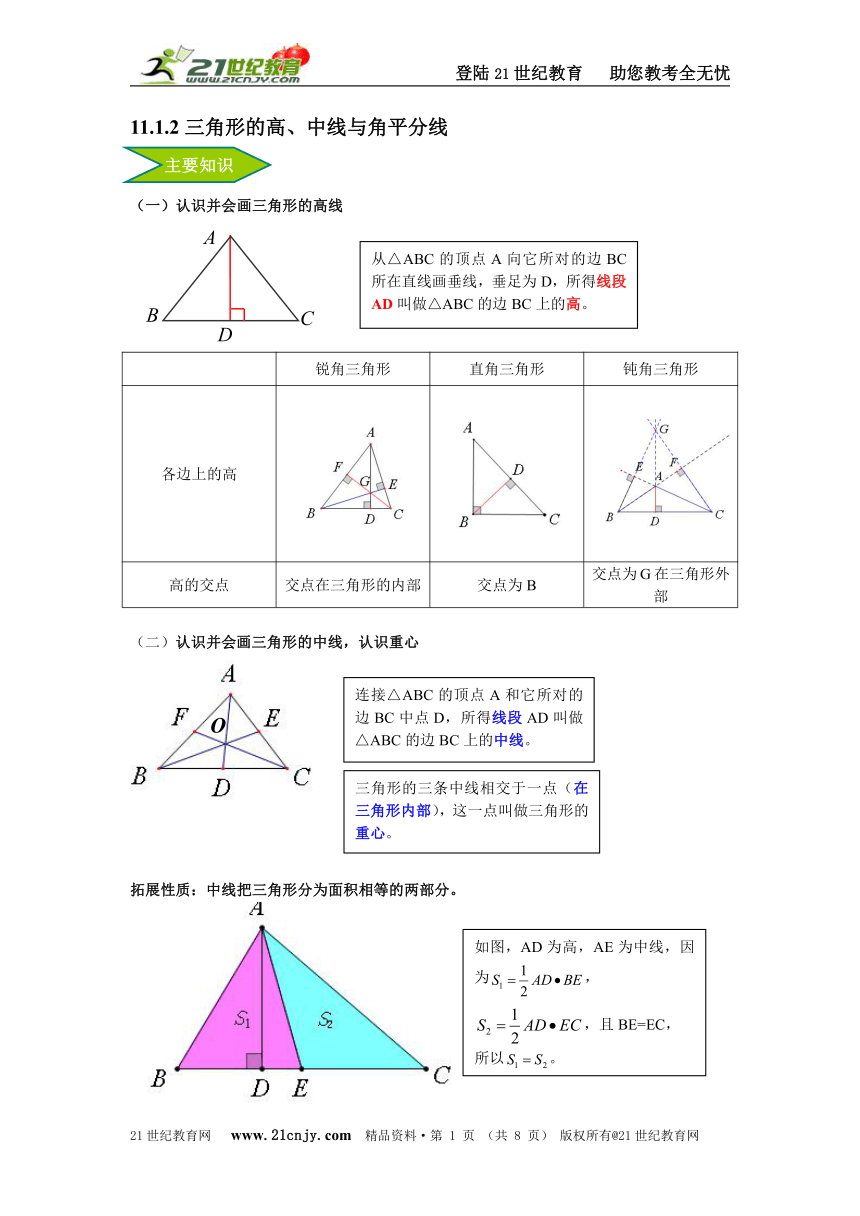 | |
| 格式 | zip | ||
| 文件大小 | 221.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-22 13:19:27 | ||
图片预览



文档简介
11.1.2三角形的高、中线与角平分线
(一)认识并会画三角形的高线
锐角三角形
直角三角形
钝角三角形
各边上的高
高的交点
交点在三角形的内部
交点为B
交点为G在三角形外部
(二)认识并会画三角形的中线,认识重心
拓展性质:中线把三角形分为面积相等的两部分。
(三)认识并会画三角形的角平分线
(四)高、中线和角平分线的性质和区别
高
中线
角平分线
性质
垂直于一条边
平分一条边
平分一个角
相同
都是线段
交点
内部或顶点上或外部
内部
内部
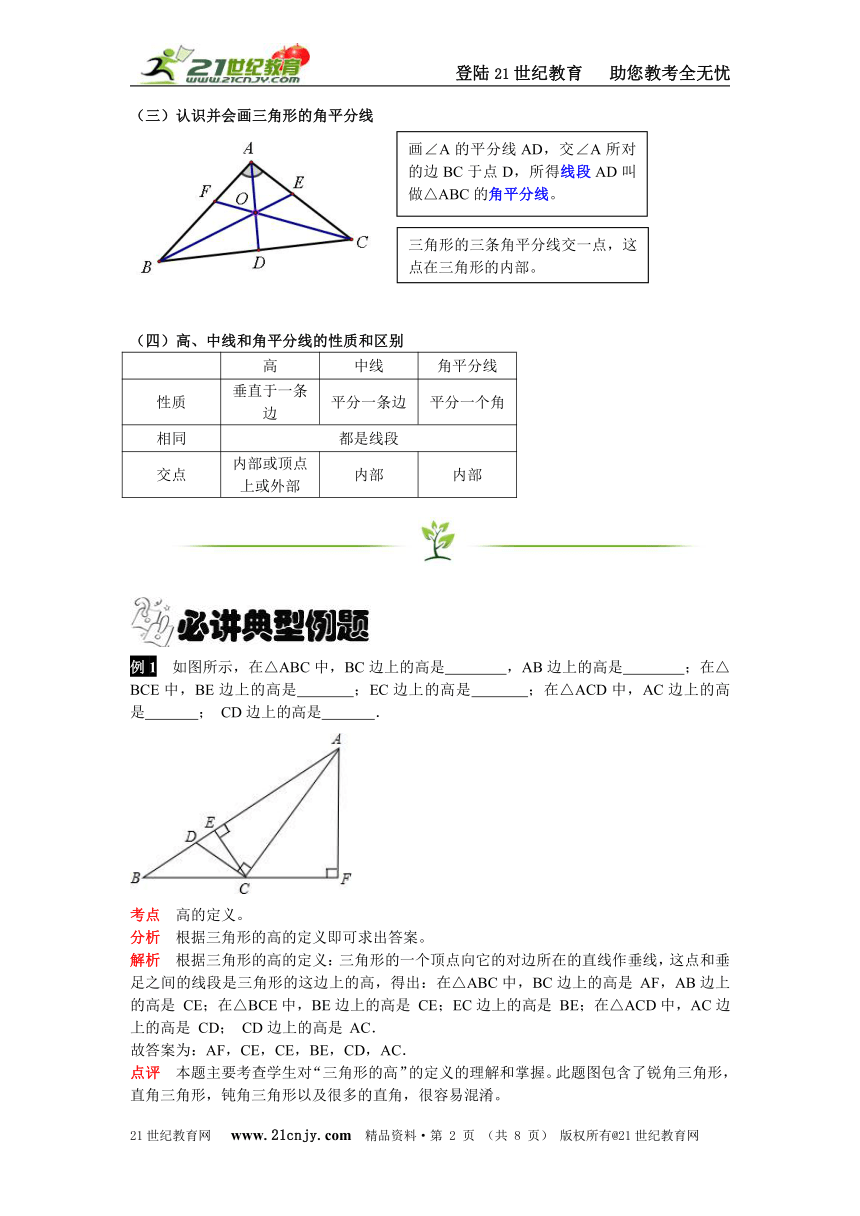
例1 如图所示,在△ABC中,BC边上的高是 ,AB边上的高是 ;在△BCE中,BE边上的高是 ;EC边上的高是 ;在△ACD中,AC边上的高是 ; CD边上的高是 . 21教育网
考点 高的定义。
分析 根据三角形的高的定义即可求出答案。
解析 根据三角形的高的定义:三角形的一个顶点向它的对边所在的直线作垂线,这点和垂足之间的线段是三角形的这边上的高,得出:在△ABC中,BC边上的高是 AF,AB边上的高是 CE;在△BCE中,BE边上的高是 CE;EC边上的高是 BE;在△ACD中,AC边上的高是 CD; CD边上的高是 AC.21·cn·jy·com
故答案为:AF,CE,CE,BE,CD,AC.
点评 本题主要考查学生对“三角形的高”的定义的理解和掌握。此题图包含了锐角三角形,直角三角形,钝角三角形以及很多的直角,很容易混淆。www.21-cn-jy.com
解题技巧 要清楚锐角三角形,直角三角形和钝角三角形的高的区别。
例2 (2013-2014学年山东省冠县武训高级中学《三角形》整章测试题)如图△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是 。 2·1·c·n·j·y
考点 三角形的中线的性质。
分析 由三角形的中线的性质可推理得“三角形的中线将三角形分成两个面积相等的三角形”。已知△ABC的面积,而且AD、BE分别是BC和AD上的中线,从而可求得。
解析 因为AD是△ABC的中线,所以=。因为BE是△ABD的中线,所以=6。
点评 掌握“三角形的中线,不仅平分一条边,而且将三角形平分成两个面积相等的三角形”的性质。
例3 已知,如图,AE是∠BAC的平分线,∠1=∠D.
求证:∠1=∠2.
考点 平行线的性质;三角形的角平分线的性质。
分析 由∠1=∠D,根据同位角相等,两直线平行可证AE∥DC,根据两直线平行,内错角相等可证∠EAC=∠2,再根据角平分线的性质即可求解.21·世纪*教育网
解 证明:∵∠1=∠D,
∴AE∥DC(同位角相等,两直线平行),
∴∠EAC=∠2(两直线平行,内错角相等),
∵AE是∠BAC的平分线,
∴∠1=∠EAC,
∴∠1=∠2.
点评 题目不难,平行线的性质是七下的知识,学生可能一下子想不出来,需要老师加以引导。
例4 △ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)∠B=30°,∠C=70°,求∠EAD的大小.
(2)若∠B<∠C,则2∠EAD与∠C-∠B是否相等?若相等,请说明理由.
考点 三角形的高和角平分线。
分析 (1)由三角形内角和定理可求得∠BAC的度数,在△ADC中,AD⊥CD,可求得
∠DAC的度数,AE是角平分线,有∠EAC=∠BAC,故∠EAD=∠EAC-∠DAC;
(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
解 (1)∵∠B=30°,∠C=70°
∴∠BAC=180°-∠B-∠C=80°
∵AE是角平分线,
∴∠EAC=∠BAC=40°
∵AD是高,∠C=70°
∴∠DAC=90°-∠C=20°
∴∠EAD=∠EAC-∠DAC=40°-20°=20°;
(2)由(1)知,∠EAD=∠EAC-∠DAC=∠BAC-(90°-∠C)①
把∠BAC=180°-∠B-∠C代入①,整理得∠EAD=∠C-∠B,
∴2∠EAD=∠C-∠B.
点评 (1)题根据三角形的高和角平分线的性质,求出一些相关的角度,即可角得。(1)题给(2)题提供了解题思路。www-2-1-cnjy-com
一课三练
基础知识
1. (2013-2014学年广东省广州市南沙区珠江中学八年级月考)下列各图中,正确画出AC边上的高的是( ) 2-1-c-n-j-y
A B C D
2.(2013-2014学年湖北省咸宁市咸安区红旗路中学期中试卷题)如果三角形的三条高线的交点在三角形的内部,那么这个三角形是( ) 【出处:21教育名师】
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3. 如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
A.2 B.3 C.4 D.6
4. (2013-2014学年河北省廊坊市大城臧屯三中期中考试题)如图1,在△ABC中,BE是中线,AD是角平分线,AD与BE相交于点O,连接DE. ①AO是△ABE的中线;②BO是△ABD的角平分线;③DE是△ADC的中线;④ED是△EBC的中线,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
第4题 第5题
5. 如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差= 。2【来源:21cnj*y.co*m】
6. (2013-2014学年江苏省盐城市盐都区期中试题)如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数。 21教育名师原创作品
能力提升
1.(常考概念题)一定在△ABC内部的线段是( )
A.锐角三角形的三条高、三条角平分线、三条中线
B.钝角三角形的三条高、三条中线、一条角平分线
C.任意三角形的一条中线、二条角平分线、三条高
D.直角三角形的三条高、三条角平分线、三条中线
2. (2013-2014学年广东省广州市南沙珠江中学期中试题)能把一个任意三角形分成面积相等的两部分是( )21世纪教育网版权所有
A.角平分线 B.中线 C.高 D.A、B、C都可以
3. 如图,在△ABC中,CD平分∠ACB,DE∥AC,DC∥EF,则与∠ACD相等角有( )个。【版权所有:21教育】
A.2 B.3 C.4 D.5
4. 如图,在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是 。
5. (2013-2014学年江苏省南京市高淳区期中试题)如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点。若△ABC的面积=12,则 。
6. (2013-2014学年江苏省靖江市靖城中学期中联考试题)如图,AD为△ABC的中线,
(1)作△ABD的中线BE;
(2)作△BED的BD边上的高EF;
(3)若△ABC的面积为60,BD=10,则点E到BC边的距离为多少?
钻研博学
1. (2014浙江省杭州2014年中考模拟题)设点P是△ABC内任意一点.现给出如下结论:
①过点P至少存在一条直线将△ABC分成周长相等的两部分;
②过点P至少存在一条直线将△ABC分成面积相等的两部分;
③过点P至多存在一条直线将△ABC分成面积相等的两部分;
④△ABC内存在点Q,过点Q有两条直线将其平分成面积相等的四个部分.
其中结论正确的是 .(写出所有正确结论的序号)
2. 如图所示,在△ABC中,AB =AC,AC上的中线把三角形的周长分为24 cm和30 cm的两个部分,求三角形各边的长. 21*cnjy*com
3. (2013-2014学年江苏省盐城市盐都区期中试题)我们知道三角形一边上的中线将这个三角形分成两个面积相等的三角形.如图1,AD是△ABC边BC上的中线,则S△ABD=S△ACD.
(1)如图2,△ABC的中线AD、BE相交于点F,△ABF与四边形CEFD的面积有怎样的数量关系?为什么?21*cnjy*com
(2)如图3,在△ABC中,已知点D、E、F分别是线段BC、AD、CE的中点,且S△ABC=8,求△BEF的面积S△BEF。【来源:21·世纪·教育·网】
(3)如图4,△ABC的面积为1.分别倍长(延长一倍)AB,BC,CA得到△A1B1C1.再分别倍长A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长n次后得到的△AnBnCn的面积为 。21cnjy.com
一课三练参考答案:
基础知识
1.D 2.A 3.C 4.A 5.2 6.120°
能力提升
1.A 2.B 3.C 4.1钻研博学
3. (1)答:S△ABF=S四边形CEFD.理由:
解:如图,∵AD和BE是△ABC的两条中线,
∴△ABD面积=△ACD面积,△BCE面积=△ABE面积,
即S1+S4=S2+S3①,S2+S4=S1+S3②,
①-②得:S1-S2=S2-S1,
∴S1=S2.∴S△ABF=S四边形CEFD.
(2)解:∵点D、E分别为BC、AD的中点,∴S△ABD=S△ACD=S△ABC,
S△BDE=S△ABD= S△ABC,S△CDE=S△ACD=S△ABC,
∴S△BCE=S△BDE+S△CDE=S△ABC+S△ABC=S△ABC,
∵F是CE的中点,
∴S△BEF=S△BCE=×S△ABC=S△ABC,
∴S△BEF:S△ABC=1:4.
又∵S△ABC=8
∴S△BEF=2.
(3)
(一)认识并会画三角形的高线
锐角三角形
直角三角形
钝角三角形
各边上的高
高的交点
交点在三角形的内部
交点为B
交点为G在三角形外部
(二)认识并会画三角形的中线,认识重心
拓展性质:中线把三角形分为面积相等的两部分。
(三)认识并会画三角形的角平分线
(四)高、中线和角平分线的性质和区别
高
中线
角平分线
性质
垂直于一条边
平分一条边
平分一个角
相同
都是线段
交点
内部或顶点上或外部
内部
内部
例1 如图所示,在△ABC中,BC边上的高是 ,AB边上的高是 ;在△BCE中,BE边上的高是 ;EC边上的高是 ;在△ACD中,AC边上的高是 ; CD边上的高是 . 21教育网
考点 高的定义。
分析 根据三角形的高的定义即可求出答案。
解析 根据三角形的高的定义:三角形的一个顶点向它的对边所在的直线作垂线,这点和垂足之间的线段是三角形的这边上的高,得出:在△ABC中,BC边上的高是 AF,AB边上的高是 CE;在△BCE中,BE边上的高是 CE;EC边上的高是 BE;在△ACD中,AC边上的高是 CD; CD边上的高是 AC.21·cn·jy·com
故答案为:AF,CE,CE,BE,CD,AC.
点评 本题主要考查学生对“三角形的高”的定义的理解和掌握。此题图包含了锐角三角形,直角三角形,钝角三角形以及很多的直角,很容易混淆。www.21-cn-jy.com
解题技巧 要清楚锐角三角形,直角三角形和钝角三角形的高的区别。
例2 (2013-2014学年山东省冠县武训高级中学《三角形》整章测试题)如图△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是 。 2·1·c·n·j·y
考点 三角形的中线的性质。
分析 由三角形的中线的性质可推理得“三角形的中线将三角形分成两个面积相等的三角形”。已知△ABC的面积,而且AD、BE分别是BC和AD上的中线,从而可求得。
解析 因为AD是△ABC的中线,所以=。因为BE是△ABD的中线,所以=6。
点评 掌握“三角形的中线,不仅平分一条边,而且将三角形平分成两个面积相等的三角形”的性质。
例3 已知,如图,AE是∠BAC的平分线,∠1=∠D.
求证:∠1=∠2.
考点 平行线的性质;三角形的角平分线的性质。
分析 由∠1=∠D,根据同位角相等,两直线平行可证AE∥DC,根据两直线平行,内错角相等可证∠EAC=∠2,再根据角平分线的性质即可求解.21·世纪*教育网
解 证明:∵∠1=∠D,
∴AE∥DC(同位角相等,两直线平行),
∴∠EAC=∠2(两直线平行,内错角相等),
∵AE是∠BAC的平分线,
∴∠1=∠EAC,
∴∠1=∠2.
点评 题目不难,平行线的性质是七下的知识,学生可能一下子想不出来,需要老师加以引导。
例4 △ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)∠B=30°,∠C=70°,求∠EAD的大小.
(2)若∠B<∠C,则2∠EAD与∠C-∠B是否相等?若相等,请说明理由.
考点 三角形的高和角平分线。
分析 (1)由三角形内角和定理可求得∠BAC的度数,在△ADC中,AD⊥CD,可求得
∠DAC的度数,AE是角平分线,有∠EAC=∠BAC,故∠EAD=∠EAC-∠DAC;
(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
解 (1)∵∠B=30°,∠C=70°
∴∠BAC=180°-∠B-∠C=80°
∵AE是角平分线,
∴∠EAC=∠BAC=40°
∵AD是高,∠C=70°
∴∠DAC=90°-∠C=20°
∴∠EAD=∠EAC-∠DAC=40°-20°=20°;
(2)由(1)知,∠EAD=∠EAC-∠DAC=∠BAC-(90°-∠C)①
把∠BAC=180°-∠B-∠C代入①,整理得∠EAD=∠C-∠B,
∴2∠EAD=∠C-∠B.
点评 (1)题根据三角形的高和角平分线的性质,求出一些相关的角度,即可角得。(1)题给(2)题提供了解题思路。www-2-1-cnjy-com
一课三练
基础知识
1. (2013-2014学年广东省广州市南沙区珠江中学八年级月考)下列各图中,正确画出AC边上的高的是( ) 2-1-c-n-j-y
A B C D
2.(2013-2014学年湖北省咸宁市咸安区红旗路中学期中试卷题)如果三角形的三条高线的交点在三角形的内部,那么这个三角形是( ) 【出处:21教育名师】
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3. 如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
A.2 B.3 C.4 D.6
4. (2013-2014学年河北省廊坊市大城臧屯三中期中考试题)如图1,在△ABC中,BE是中线,AD是角平分线,AD与BE相交于点O,连接DE. ①AO是△ABE的中线;②BO是△ABD的角平分线;③DE是△ADC的中线;④ED是△EBC的中线,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
第4题 第5题
5. 如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差= 。2【来源:21cnj*y.co*m】
6. (2013-2014学年江苏省盐城市盐都区期中试题)如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数。 21教育名师原创作品
能力提升
1.(常考概念题)一定在△ABC内部的线段是( )
A.锐角三角形的三条高、三条角平分线、三条中线
B.钝角三角形的三条高、三条中线、一条角平分线
C.任意三角形的一条中线、二条角平分线、三条高
D.直角三角形的三条高、三条角平分线、三条中线
2. (2013-2014学年广东省广州市南沙珠江中学期中试题)能把一个任意三角形分成面积相等的两部分是( )21世纪教育网版权所有
A.角平分线 B.中线 C.高 D.A、B、C都可以
3. 如图,在△ABC中,CD平分∠ACB,DE∥AC,DC∥EF,则与∠ACD相等角有( )个。【版权所有:21教育】
A.2 B.3 C.4 D.5
4. 如图,在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是 。
5. (2013-2014学年江苏省南京市高淳区期中试题)如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点。若△ABC的面积=12,则 。
6. (2013-2014学年江苏省靖江市靖城中学期中联考试题)如图,AD为△ABC的中线,
(1)作△ABD的中线BE;
(2)作△BED的BD边上的高EF;
(3)若△ABC的面积为60,BD=10,则点E到BC边的距离为多少?
钻研博学
1. (2014浙江省杭州2014年中考模拟题)设点P是△ABC内任意一点.现给出如下结论:
①过点P至少存在一条直线将△ABC分成周长相等的两部分;
②过点P至少存在一条直线将△ABC分成面积相等的两部分;
③过点P至多存在一条直线将△ABC分成面积相等的两部分;
④△ABC内存在点Q,过点Q有两条直线将其平分成面积相等的四个部分.
其中结论正确的是 .(写出所有正确结论的序号)
2. 如图所示,在△ABC中,AB =AC,AC上的中线把三角形的周长分为24 cm和30 cm的两个部分,求三角形各边的长. 21*cnjy*com
3. (2013-2014学年江苏省盐城市盐都区期中试题)我们知道三角形一边上的中线将这个三角形分成两个面积相等的三角形.如图1,AD是△ABC边BC上的中线,则S△ABD=S△ACD.
(1)如图2,△ABC的中线AD、BE相交于点F,△ABF与四边形CEFD的面积有怎样的数量关系?为什么?21*cnjy*com
(2)如图3,在△ABC中,已知点D、E、F分别是线段BC、AD、CE的中点,且S△ABC=8,求△BEF的面积S△BEF。【来源:21·世纪·教育·网】
(3)如图4,△ABC的面积为1.分别倍长(延长一倍)AB,BC,CA得到△A1B1C1.再分别倍长A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长n次后得到的△AnBnCn的面积为 。21cnjy.com
一课三练参考答案:
基础知识
1.D 2.A 3.C 4.A 5.2 6.120°
能力提升
1.A 2.B 3.C 4.1
3. (1)答:S△ABF=S四边形CEFD.理由:
解:如图,∵AD和BE是△ABC的两条中线,
∴△ABD面积=△ACD面积,△BCE面积=△ABE面积,
即S1+S4=S2+S3①,S2+S4=S1+S3②,
①-②得:S1-S2=S2-S1,
∴S1=S2.∴S△ABF=S四边形CEFD.
(2)解:∵点D、E分别为BC、AD的中点,∴S△ABD=S△ACD=S△ABC,
S△BDE=S△ABD= S△ABC,S△CDE=S△ACD=S△ABC,
∴S△BCE=S△BDE+S△CDE=S△ABC+S△ABC=S△ABC,
∵F是CE的中点,
∴S△BEF=S△BCE=×S△ABC=S△ABC,
∴S△BEF:S△ABC=1:4.
又∵S△ABC=8
∴S△BEF=2.
(3)
