广东省揭阳市普宁市侨中2022-2023学年高一下学期5月月考数学试题(含答案)
文档属性
| 名称 | 广东省揭阳市普宁市侨中2022-2023学年高一下学期5月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 826.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 21:48:12 | ||
图片预览



文档简介
普宁市侨中2022-2023学年高一下学期5月月考
数学科试题
说明:1.本试题共4页,满分150分,考试时间120分钟。
2.答题前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、试室号、座位号填写在答题卷上。
3. 答题必须使用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷上各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.考生必须保持答题卷整洁,考试结束后,将答题卷交回,试卷自己保存。
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若,则( )
A. B. C.1 D.2
2.在学生人数比例为2:3:5的A,B,C三所学校中,用分层抽样方法招募n名志愿者,若在A学校恰好选出了6名志愿者,那么n=( )
A.9 B.15 C.24 D.30
3.已知,,则( )
A. 1 B. 2 C. 3 D. 4
4.已知向量,的夹角为,,,则( )
A. 4 B. 5 C. D.
5. 在正方体中,为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
6、设m、n是两条不同的直线,是三个不同的平面,给出下列四个命题:
①若,,则 ②若,,,则
③若,,则 ④若,,则
其中正确命题的序号是( )
A.①和② B.②和③ C.③和④ D.①和④
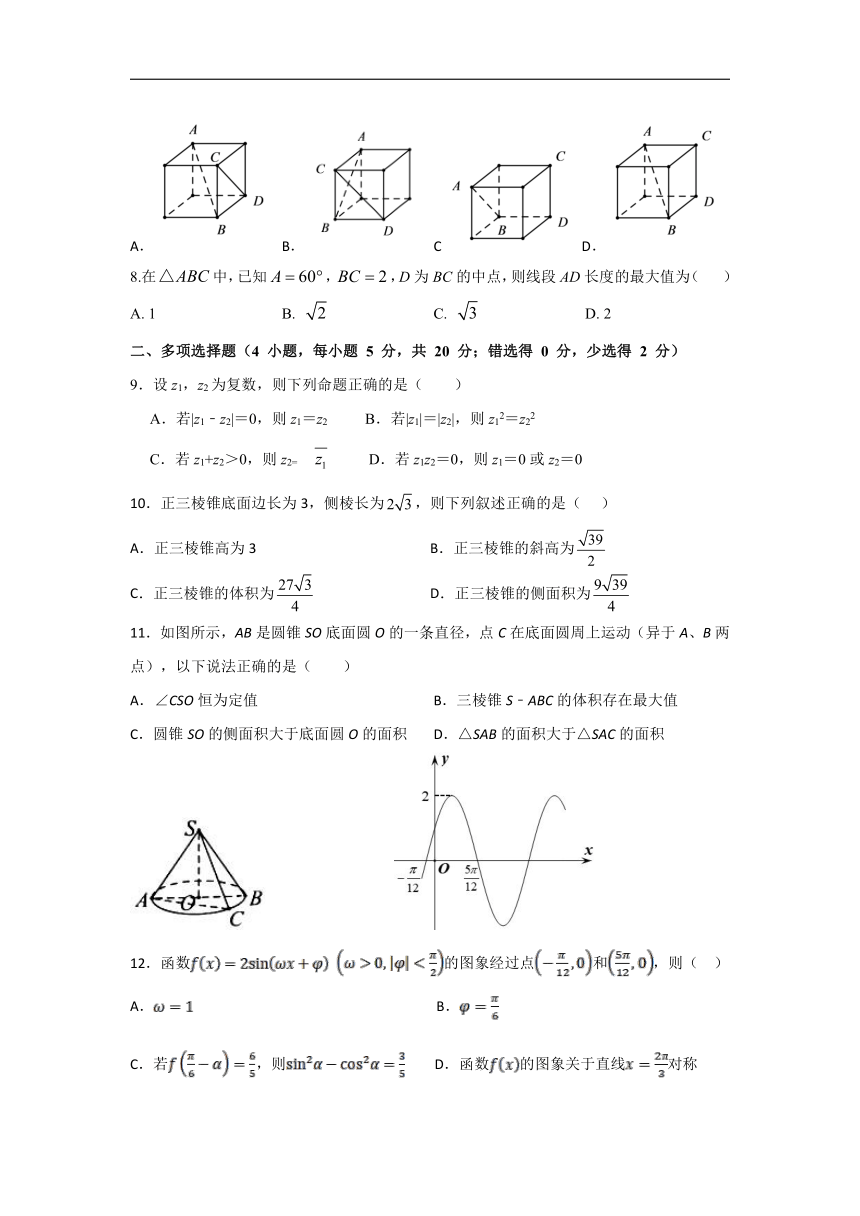
7.在下列四个正方体中,能得出的是( )
A. B. CD.
8.在中,已知,,D为BC的中点,则线段AD长度的最大值为( )
A. 1 B. C. D. 2
二、多项选择题(4 小题,每小题 5 分,共 20 分;错选得 0 分,少选得 2 分)
9.设z1,z2为复数,则下列命题正确的是( )
A.若|z1﹣z2|=0,则z1=z2 B.若|z1|=|z2|,则z12=z22
C.若z1+z2>0,则z2= D.若z1z2=0,则z1=0或z2=0
10.正三棱锥底面边长为3,侧棱长为,则下列叙述正确的是( )
A.正三棱锥高为3 B.正三棱锥的斜高为
C.正三棱锥的体积为 D.正三棱锥的侧面积为
11.如图所示,AB是圆锥SO底面圆O的一条直径,点C在底面圆周上运动(异于A、B两点),以下说法正确的是( )
A.∠CSO恒为定值 B.三棱锥S﹣ABC的体积存在最大值
C.圆锥SO的侧面积大于底面圆O的面积 D.△SAB的面积大于△SAC的面积
12.函数 的图象经过点和,则( )
A. B.
C.若,则 D.函数的图象关于直线对称
三、填空题(4 小题,每小题 5 分,共 20 分)
13. 设一个圆锥的侧面展开图是半径为的半圆,则此圆锥的体积为 .
14.如图,在中,,点P是线段BN上的一点,若,则实数= .
如图,正方体中,E F分别是棱 的中点,则正方体被截面BEFC分成两部分的体积之比___________.
16.已知正方形的边长为2,为的中点,则 .
四、解答题(本大题共6小题,共70分)
17.(10分)(1)已知复数,,若为纯虚数,求的值;
(2)已知复数z满足,求a的值.
18.(12分)设平面三点A(-2,1),B(4,-1),C(2,3).
(1)若试求D点的坐标;
(2)试求向量与的夹角余弦值。
19.(12分)已知内角的对边分别为,且.
(1)求角;
(2)若的周长为,且外接圆的半径为1,求的面积.
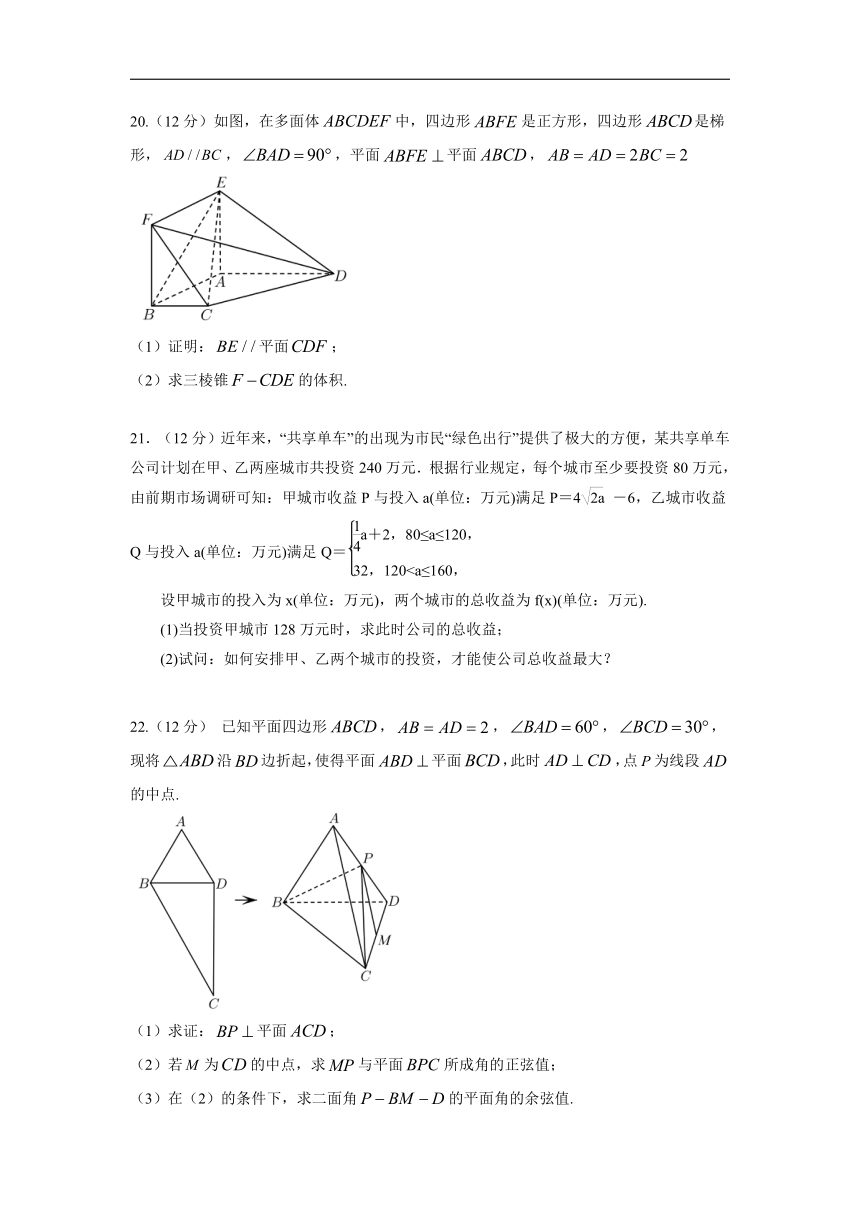
20.(12分)如图,在多面体中,四边形是正方形,四边形是梯形,,,平面平面,
(1)证明:平面;
(2)求三棱锥的体积.
21.(12分)近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元.根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益P与投入a(单位:万元)满足P=4-6,乙城市收益Q与投入a(单位:万元)满足Q=
设甲城市的投入为x(单位:万元),两个城市的总收益为f(x)(单位:万元).
(1)当投资甲城市128万元时,求此时公司的总收益;
(2)试问:如何安排甲、乙两个城市的投资,才能使公司总收益最大?
22.(12分) 已知平面四边形,,,,现将沿边折起,使得平面平面,此时,点为线段的中点.
(1)求证:平面;
(2)若为的中点,求与平面所成角的正弦值;
(3)在(2)的条件下,求二面角的平面角的余弦值.
普宁市侨中2022-2023学年高一下学期5月月考
数学科答案
一、DDABD AAC 二、9.AD; 10.ABD; 11.ABC; 12.BD
三、13.3π 14. 15 . 3 16. 2
17.(1)若为纯虚数,则,………………………………………………3分
解得;…………………………………………………………………………………5分
(2)依题意,,……………………………………7分
因此,………………………………………………………9分
解得,……………………………………………………………………………………10分
18(1)设,则,………………………………2分
因为所以,解得………………………………………………4分
所以D点的坐标为.……………………………………………………………………6分
由(1)知,又,…………………………………………7分
∵,.………………………………8分
,…………………………………10分
所以,
故向量与的夹角余弦值为.……………………………………………………12分
19.(1)由题意,
由正弦定理得,………………………………………1分
因为,……………………………………………2分
所以,…………………………………………………………3分
因为,所以,所以,……………………………………………4分
又,所以.…………………………………………………………………6分
(2)设外接圆的半径为,则,由正弦定理得,…………7分
因为的周长为,所以,………………………………………………8分
由余弦定理得,即,所以,……9分
由得,…………………………………………………………………11分
所以的面积 .………………………………12分
20.(12分)如图,过作交于,连接 ,设交于点,连接.由,,则四边形为平行四边形,所以,而且,则且,所以四边形为平行四边形,则为线段的中点,又,在△中为中位线,故,……5分 又平面,平面,所以平面.………………6分
【小问2详解】由(1)知:平面,
故到平面的距离与点到平面的距离相等.
所以.……………8分
面面,面面,,面,
所以面.……10分
则.……12分
21.(12分)(1)当x=128,即甲城市投资128万元时,乙城市投资112万元,
所以f(128)=4×-6+×112+2=88(万元).
因此,此时公司的总收益为88万元.………4分
(2)由题意知,甲城市投资x万元,则乙城市投资(240-x)万元,
依题意得 解之得80≤x≤160,………6分
当80≤x<120,即120<240-x≤160时,
f(x)=4-6+32=4+26<26+16.………7分
当120≤x≤160,即80≤240-x≤120时,
f(x)=4-6+(240-x)+2=-x+4+56.………9分
令t=,则t∈[2,4],
所以y=-t2+4t+56=-(t-8)2+88.………10分
当t=8,即x=128时,y取最大值88.
因为88-(26+16)=2×(31-8)>0,
故f(x)的最大值为88.因此,当甲城市投资128万元,乙城市投资112万元时,总收益最大,且最大收益为88万元.………12分
22.(12分) 【小问1详解】因为 所以为等边三角形,
因为为的中点,所以.………1分
取的中点,连接,,则,………2分
因为平面平面平面平面平面,
所以平面,又平面,所以………3分
因为平面所以平面
因为平面所以
又因为平面,所以平面.………4分
【小问2详解】过点作,垂足为.如图所示
由(1)知,平面.因为平面,所以,所以平面,
所以为与平面所成角.………5分
由(1)知,平面平面,所以.
在中,,,………6分
因为为的中点,所以.
在中,,
中,,
在中,,
所以.
所以与平面所成角的正弦值为.………8分
【小问3详解】取的中点为,连接,因为为线段的中点,
所以,
由(1)知,平面,所以平面,平面.
所以.
过点作,垂足为,连接,,平面,
所以平面.平面.所以,
所以为二面角的平面角.………9分
在中,,
由(1)知,为等边三角形,为线段的中点,
所以
由(1)知,平面.平面.所以,
在中,,由(2)知,
即,解得.………10分
因为平面.平面.所以.
在中,.
.
所以二面角的平面角的余弦值为.………12分
数学科试题
说明:1.本试题共4页,满分150分,考试时间120分钟。
2.答题前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、试室号、座位号填写在答题卷上。
3. 答题必须使用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷上各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.考生必须保持答题卷整洁,考试结束后,将答题卷交回,试卷自己保存。
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若,则( )
A. B. C.1 D.2
2.在学生人数比例为2:3:5的A,B,C三所学校中,用分层抽样方法招募n名志愿者,若在A学校恰好选出了6名志愿者,那么n=( )
A.9 B.15 C.24 D.30
3.已知,,则( )
A. 1 B. 2 C. 3 D. 4
4.已知向量,的夹角为,,,则( )
A. 4 B. 5 C. D.
5. 在正方体中,为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
6、设m、n是两条不同的直线,是三个不同的平面,给出下列四个命题:
①若,,则 ②若,,,则
③若,,则 ④若,,则
其中正确命题的序号是( )
A.①和② B.②和③ C.③和④ D.①和④
7.在下列四个正方体中,能得出的是( )
A. B. CD.
8.在中,已知,,D为BC的中点,则线段AD长度的最大值为( )
A. 1 B. C. D. 2
二、多项选择题(4 小题,每小题 5 分,共 20 分;错选得 0 分,少选得 2 分)
9.设z1,z2为复数,则下列命题正确的是( )
A.若|z1﹣z2|=0,则z1=z2 B.若|z1|=|z2|,则z12=z22
C.若z1+z2>0,则z2= D.若z1z2=0,则z1=0或z2=0
10.正三棱锥底面边长为3,侧棱长为,则下列叙述正确的是( )
A.正三棱锥高为3 B.正三棱锥的斜高为
C.正三棱锥的体积为 D.正三棱锥的侧面积为
11.如图所示,AB是圆锥SO底面圆O的一条直径,点C在底面圆周上运动(异于A、B两点),以下说法正确的是( )
A.∠CSO恒为定值 B.三棱锥S﹣ABC的体积存在最大值
C.圆锥SO的侧面积大于底面圆O的面积 D.△SAB的面积大于△SAC的面积
12.函数 的图象经过点和,则( )
A. B.
C.若,则 D.函数的图象关于直线对称
三、填空题(4 小题,每小题 5 分,共 20 分)
13. 设一个圆锥的侧面展开图是半径为的半圆,则此圆锥的体积为 .
14.如图,在中,,点P是线段BN上的一点,若,则实数= .
如图,正方体中,E F分别是棱 的中点,则正方体被截面BEFC分成两部分的体积之比___________.
16.已知正方形的边长为2,为的中点,则 .
四、解答题(本大题共6小题,共70分)
17.(10分)(1)已知复数,,若为纯虚数,求的值;
(2)已知复数z满足,求a的值.
18.(12分)设平面三点A(-2,1),B(4,-1),C(2,3).
(1)若试求D点的坐标;
(2)试求向量与的夹角余弦值。
19.(12分)已知内角的对边分别为,且.
(1)求角;
(2)若的周长为,且外接圆的半径为1,求的面积.
20.(12分)如图,在多面体中,四边形是正方形,四边形是梯形,,,平面平面,
(1)证明:平面;
(2)求三棱锥的体积.
21.(12分)近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元.根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益P与投入a(单位:万元)满足P=4-6,乙城市收益Q与投入a(单位:万元)满足Q=
设甲城市的投入为x(单位:万元),两个城市的总收益为f(x)(单位:万元).
(1)当投资甲城市128万元时,求此时公司的总收益;
(2)试问:如何安排甲、乙两个城市的投资,才能使公司总收益最大?
22.(12分) 已知平面四边形,,,,现将沿边折起,使得平面平面,此时,点为线段的中点.
(1)求证:平面;
(2)若为的中点,求与平面所成角的正弦值;
(3)在(2)的条件下,求二面角的平面角的余弦值.
普宁市侨中2022-2023学年高一下学期5月月考
数学科答案
一、DDABD AAC 二、9.AD; 10.ABD; 11.ABC; 12.BD
三、13.3π 14. 15 . 3 16. 2
17.(1)若为纯虚数,则,………………………………………………3分
解得;…………………………………………………………………………………5分
(2)依题意,,……………………………………7分
因此,………………………………………………………9分
解得,……………………………………………………………………………………10分
18(1)设,则,………………………………2分
因为所以,解得………………………………………………4分
所以D点的坐标为.……………………………………………………………………6分
由(1)知,又,…………………………………………7分
∵,.………………………………8分
,…………………………………10分
所以,
故向量与的夹角余弦值为.……………………………………………………12分
19.(1)由题意,
由正弦定理得,………………………………………1分
因为,……………………………………………2分
所以,…………………………………………………………3分
因为,所以,所以,……………………………………………4分
又,所以.…………………………………………………………………6分
(2)设外接圆的半径为,则,由正弦定理得,…………7分
因为的周长为,所以,………………………………………………8分
由余弦定理得,即,所以,……9分
由得,…………………………………………………………………11分
所以的面积 .………………………………12分
20.(12分)如图,过作交于,连接 ,设交于点,连接.由,,则四边形为平行四边形,所以,而且,则且,所以四边形为平行四边形,则为线段的中点,又,在△中为中位线,故,……5分 又平面,平面,所以平面.………………6分
【小问2详解】由(1)知:平面,
故到平面的距离与点到平面的距离相等.
所以.……………8分
面面,面面,,面,
所以面.……10分
则.……12分
21.(12分)(1)当x=128,即甲城市投资128万元时,乙城市投资112万元,
所以f(128)=4×-6+×112+2=88(万元).
因此,此时公司的总收益为88万元.………4分
(2)由题意知,甲城市投资x万元,则乙城市投资(240-x)万元,
依题意得 解之得80≤x≤160,………6分
当80≤x<120,即120<240-x≤160时,
f(x)=4-6+32=4+26<26+16.………7分
当120≤x≤160,即80≤240-x≤120时,
f(x)=4-6+(240-x)+2=-x+4+56.………9分
令t=,则t∈[2,4],
所以y=-t2+4t+56=-(t-8)2+88.………10分
当t=8,即x=128时,y取最大值88.
因为88-(26+16)=2×(31-8)>0,
故f(x)的最大值为88.因此,当甲城市投资128万元,乙城市投资112万元时,总收益最大,且最大收益为88万元.………12分
22.(12分) 【小问1详解】因为 所以为等边三角形,
因为为的中点,所以.………1分
取的中点,连接,,则,………2分
因为平面平面平面平面平面,
所以平面,又平面,所以………3分
因为平面所以平面
因为平面所以
又因为平面,所以平面.………4分
【小问2详解】过点作,垂足为.如图所示
由(1)知,平面.因为平面,所以,所以平面,
所以为与平面所成角.………5分
由(1)知,平面平面,所以.
在中,,,………6分
因为为的中点,所以.
在中,,
中,,
在中,,
所以.
所以与平面所成角的正弦值为.………8分
【小问3详解】取的中点为,连接,因为为线段的中点,
所以,
由(1)知,平面,所以平面,平面.
所以.
过点作,垂足为,连接,,平面,
所以平面.平面.所以,
所以为二面角的平面角.………9分
在中,,
由(1)知,为等边三角形,为线段的中点,
所以
由(1)知,平面.平面.所以,
在中,,由(2)知,
即,解得.………10分
因为平面.平面.所以.
在中,.
.
所以二面角的平面角的余弦值为.………12分
同课章节目录
