5.1 函数与它的表示法(3)-初中数学青岛版九年级下册 同步课件(共15张PPT)
文档属性
| 名称 | 5.1 函数与它的表示法(3)-初中数学青岛版九年级下册 同步课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 794.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
5.1 函数与它的表示法(3)
认识分段函数,会根据简单分段函数的表达式或图象求出函数值.
学习目标
为了鼓励节约用电,某市按以下标准对居民用户收费:当一户居民月用电量不超过200kw h时,按0.5元/kw h收费。当一户居民月用电量超过200kw h时,超过部分按0.7元/kw h收费。
观察与思考
(1)设用电量为x kw h ,电费为y元,你能按上述标准写出一户居民的每月应交电费y(元)与x(kw h)之间的函数表达式吗?
y=
0.5x 0≤x≤200
0.7x-40 x>200
观察与思考
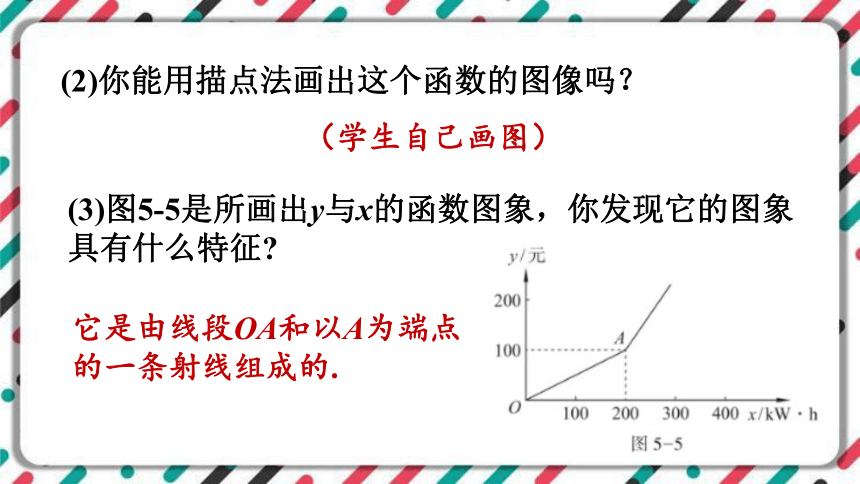
(2)你能用描点法画出这个函数的图像吗?
(3)图5-5是所画出y与x的函数图象,你发现它的图象具有什么特征
(学生自己画图)
它是由线段OA和以A为端点的一条射线组成的.
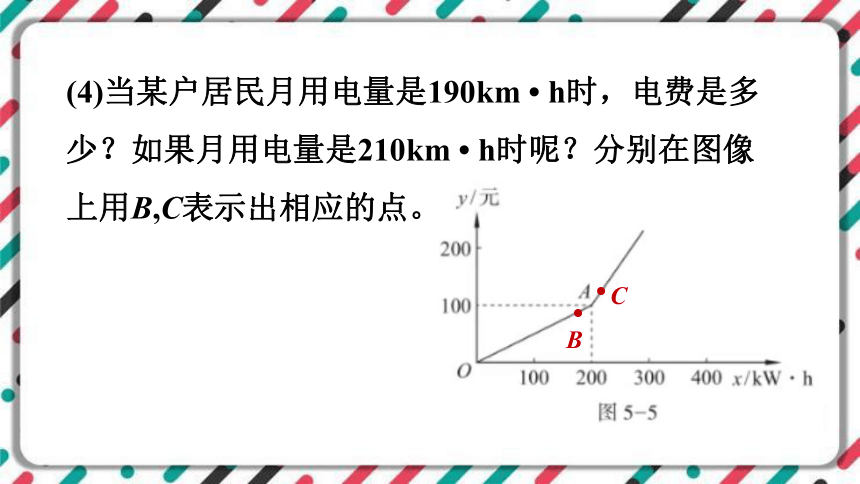
(4)当某户居民月用电量是190km h时,电费是多少?如果月用电量是210km h时呢?分别在图像上用B,C表示出相应的点。
C
B
一、分段函数定义
二、分段函数的表示方法
形如:
像这样,函数关系是分段给出的,我们称它叫做 分段函数.
(1)分段函数是一个函数,不要把它误认为是“几个函数”;
(2)分段函数的自变量取值范围是各分段取值范围的全体;
(3)每段函数表达式自变量的取值范围之间没有公共点。
注意
某校住校生放学后到学校锅炉房水箱打水,每人接水2L.开始时水箱中有水 96 L,两个龙头同时放水,经过2 min 后,水箱内的余水量为80 L.此时其中一个龙头因故障而关闭.如果前后两人接水间隔时间忽略不计,且不发生泼洒,水箱内的
余水量y(L)与放水时间x(min )的函数
图象如图 5-6.已知放水4 min时,水箱
中的余水量为72 L.
(1)写出水箱的余水量y与放水时间x之间的函数表达式;
例2
设这段函数的表达式是y=kx +b,将 (0,96),(2,80)代入该式,得
(1)由题意和图 5-6知,y与x之间的函数是分段函数.其中线段AB表示两个水龙头同时放水时y与x的对应关系.
b =96,
2k +b =80.
例2
由此得到该函数表达式是
所以这段函数的表达式是y=-8x+ 96,0≤x≤2.
同样地将(2,80),(4,72) 代入y = k x + b ,可以求出当只有一个水龙头放水时,y与x之间函数的表达式为y = -4x + 88.令y=0,得x= 22(min).所以当只有一个水龙头放水时,函数表达式是y = -4x + 88, 2<x≤22.
-8x+ 96, 0≤x≤2
-4x + 88, 2<x≤22 .
y=
(2)前15位同学接水共用了多少时间?
例2
(2)前 15位同学共接水 2×15= 30(L),当第 15 位同学接完水时水箱余水量为96 -30= 66 < 80.由图5-6可以看出,此时只有一个水龙头放水.将y=66代入y=-4x +88,得66 =-4x +88,解得x= 5.5(min).
所以,前15位同学接水共用时间 5.5 min.
(1)开挖到25 m时,用了多少时间
1. 某工程队开挖一段河渠,施工进度y( m)与施工时间x(天)之间的函数关系如图所示.根据图象所提供的信息,解答下列问题:
练习
2天
(2)写出开工后前6天内y与x之间的函数表达式;
练习
设这段函数的表达式是y=kx +b,将 (2,25),(6,50)
代入该式,得
2k+b=25,
6k+b=50.
k=6.25
b=12.5.
解得
开工后前6天内y与x之间的函数表达式6.25x+12.5=y.
一、分段函数
二、分段函数的表示方法
注意:
(1)分段函数是一个函数,不要把它误认为是“几个函数”;
(2)分段函数的自变量取值范围是各分段取值范围的全体;
(3)每段函数表达式自变量的取值范围之间没有公共点。
总结
5.1 函数与它的表示法(3)
认识分段函数,会根据简单分段函数的表达式或图象求出函数值.
学习目标
为了鼓励节约用电,某市按以下标准对居民用户收费:当一户居民月用电量不超过200kw h时,按0.5元/kw h收费。当一户居民月用电量超过200kw h时,超过部分按0.7元/kw h收费。
观察与思考
(1)设用电量为x kw h ,电费为y元,你能按上述标准写出一户居民的每月应交电费y(元)与x(kw h)之间的函数表达式吗?
y=
0.5x 0≤x≤200
0.7x-40 x>200
观察与思考
(2)你能用描点法画出这个函数的图像吗?
(3)图5-5是所画出y与x的函数图象,你发现它的图象具有什么特征
(学生自己画图)
它是由线段OA和以A为端点的一条射线组成的.
(4)当某户居民月用电量是190km h时,电费是多少?如果月用电量是210km h时呢?分别在图像上用B,C表示出相应的点。
C
B
一、分段函数定义
二、分段函数的表示方法
形如:
像这样,函数关系是分段给出的,我们称它叫做 分段函数.
(1)分段函数是一个函数,不要把它误认为是“几个函数”;
(2)分段函数的自变量取值范围是各分段取值范围的全体;
(3)每段函数表达式自变量的取值范围之间没有公共点。
注意
某校住校生放学后到学校锅炉房水箱打水,每人接水2L.开始时水箱中有水 96 L,两个龙头同时放水,经过2 min 后,水箱内的余水量为80 L.此时其中一个龙头因故障而关闭.如果前后两人接水间隔时间忽略不计,且不发生泼洒,水箱内的
余水量y(L)与放水时间x(min )的函数
图象如图 5-6.已知放水4 min时,水箱
中的余水量为72 L.
(1)写出水箱的余水量y与放水时间x之间的函数表达式;
例2
设这段函数的表达式是y=kx +b,将 (0,96),(2,80)代入该式,得
(1)由题意和图 5-6知,y与x之间的函数是分段函数.其中线段AB表示两个水龙头同时放水时y与x的对应关系.
b =96,
2k +b =80.
例2
由此得到该函数表达式是
所以这段函数的表达式是y=-8x+ 96,0≤x≤2.
同样地将(2,80),(4,72) 代入y = k x + b ,可以求出当只有一个水龙头放水时,y与x之间函数的表达式为y = -4x + 88.令y=0,得x= 22(min).所以当只有一个水龙头放水时,函数表达式是y = -4x + 88, 2<x≤22.
-8x+ 96, 0≤x≤2
-4x + 88, 2<x≤22 .
y=
(2)前15位同学接水共用了多少时间?
例2
(2)前 15位同学共接水 2×15= 30(L),当第 15 位同学接完水时水箱余水量为96 -30= 66 < 80.由图5-6可以看出,此时只有一个水龙头放水.将y=66代入y=-4x +88,得66 =-4x +88,解得x= 5.5(min).
所以,前15位同学接水共用时间 5.5 min.
(1)开挖到25 m时,用了多少时间
1. 某工程队开挖一段河渠,施工进度y( m)与施工时间x(天)之间的函数关系如图所示.根据图象所提供的信息,解答下列问题:
练习
2天
(2)写出开工后前6天内y与x之间的函数表达式;
练习
设这段函数的表达式是y=kx +b,将 (2,25),(6,50)
代入该式,得
2k+b=25,
6k+b=50.
k=6.25
b=12.5.
解得
开工后前6天内y与x之间的函数表达式6.25x+12.5=y.
一、分段函数
二、分段函数的表示方法
注意:
(1)分段函数是一个函数,不要把它误认为是“几个函数”;
(2)分段函数的自变量取值范围是各分段取值范围的全体;
(3)每段函数表达式自变量的取值范围之间没有公共点。
总结
