6.3频数直方图 同步课件(2课时、共32张PPT)2022--2023学年青岛版九年级数学下册
文档属性
| 名称 | 6.3频数直方图 同步课件(2课时、共32张PPT)2022--2023学年青岛版九年级数学下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 11:24:32 | ||
图片预览










文档简介
(共32张PPT)
6.3 频数直方图
1.了解频数直方图的概念;
2.会读频数直方图;
3.会画频数直方图.
学习目标
在统计里,我们称每个考查对象出现的次数为_______,
每个对象出现的次数与总次数的比值为 .
2.各对象的频数之和等于_________,各频率之和等于 .
3.已知一个样本中,50个数据分别落在5个组内,第一、二、
三、五的数据个数分别为2,8,15,5,则第四组的频数为
,频率为 .
频数
频率
数据总和
1
20
40%
回顾
小莹从气象网站上,收集了今年3月上旬某一天我国34个城市的最低气温(单位:°C),如下表所示:
城市 北京 哈尔滨 长春 沈阳 天津 呼和浩特 乌鲁木齐 银川 西宁 兰州 西安 拉萨 成都 重庆 贵阳 昆明 太原
最低
气温(x/°C) 4 -1 -1
-1 4 -7 -3 -1
-4 6 4 0 10 10 10 11 0
观察与思考
城市 石家庄 济南 郑州 合肥 南京 上海 武汉 长沙 南昌 杭州 福州 台北 南宁 海口 广州 香港 澳门
最低
气温(x/°C) 5 7 8 10 10 8 14 15 15 9 15 18 20 22 20 18 18
思考下列问题,并与同学交流:
(1)如何根据表中的信息设计出一个关于上述城市当天最低气温的频数、频率分布表
观察与思考
在上表中,各城市当天最低气温的最大值是22℃,最小值是-7 ℃ ,由此可知,当天最低气温数据的分布范围是
-7 ℃ —22 ℃ ,它们的差为22-(-7)=29 ( ℃ ).
观察与思考
①确定所有数据中最大值与最小值,并计算二者的差.
参照总体中数据的个数是34,数据的最大值与最小值的差是29,可以设定组数为6,由于总体中数据的最大值与最小值的差÷组数=29÷6≈4.8,为了分组方便,可取与4.8最相近的一个整数5作为组距(每组数据的上限与下限的差)于是可把总体数据按以下范围分为6组:
观察与思考
②确定组数、组距,并进行分组.
-7≤x<-2,-2 ≤x <3,3 ≤x <8, 8 ≤x <13,13 ≤x <18,18 ≤x <23.其中-2、3,8,13,18是各组的界限.
利用划记,统计各组中包含的最低气温数据的频数,并计算出相应的频率,填写下面的频数、频率分布表:
观察与思考
③列出相应的频数、频率分布表.
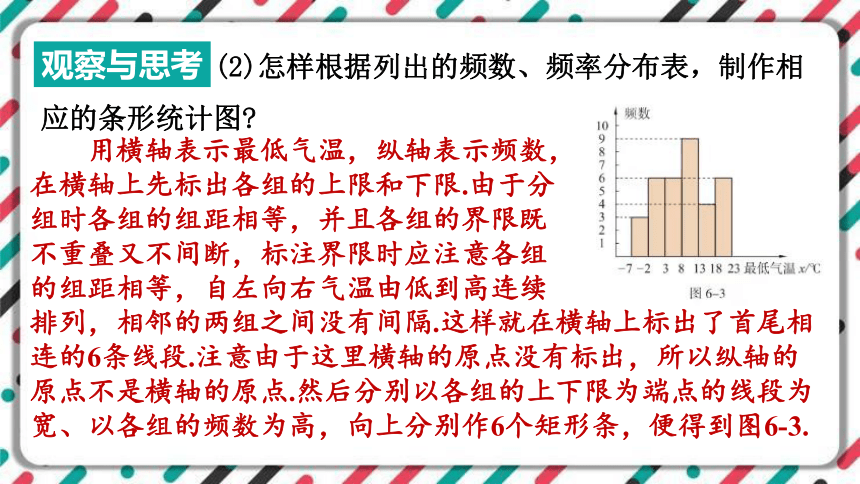
用横轴表示最低气温,纵轴表示频数,
在横轴上先标出各组的上限和下限.由于分
组时各组的组距相等,并且各组的界限既
不重叠又不间断,标注界限时应注意各组
的组距相等,自左向右气温由低到高连续
排列,相邻的两组之间没有间隔.这样就在横轴上标出了首尾相连的6条线段.注意由于这里横轴的原点没有标出,所以纵轴的原点不是横轴的原点.然后分别以各组的上下限为端点的线段为宽、以各组的频数为高,向上分别作6个矩形条,便得到图6-3.
观察与思考
(2)怎样根据列出的频数、频率分布表,制作相应的条形统计图
通过图 6-3,可以直接比较各组的频数的差异,即一个组内城市的个数与另一个组内城市的个数相差几个.
观察与思考
(3)通过观察图6-3,你能得到数据中蕴含的哪些信息 你能看出总体中三月上旬34个城市的最低气温的分布情况吗 与同学交流.
可以看出该天最低气温在8℃~13℃之间的城市最多,有9个城市,而且该组相应的小矩形在直方图的中间位置,这些城市都分布在我国地理纬度的中部地区和西南地区.
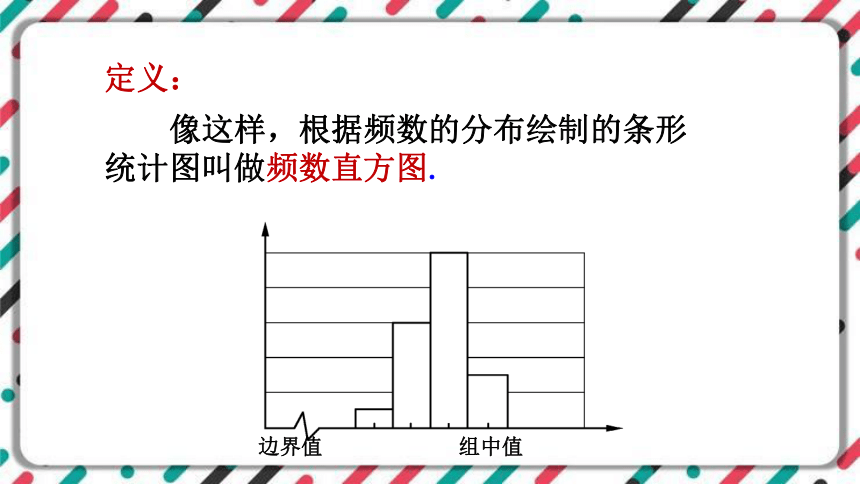
像图6-3这样根据频数的分布绘制的条形统计图叫做频数直方图。
将数据进行分组时,组数的多少应适当,组数太少,不能充分显示数据的分布情况;组数太多,不仅繁琐,且容易把性质相近的同类数据分散到各组,从而也不能正确显示数据分布的特征和规律。
一般的,数据在100个以内,可按情况分为5~12组。
加油站
像这样,根据频数的分布绘制的条形统计图叫做频数直方图.
边界值
组中值
定义:
(1) 计算极差
(2) 决定组距与组数.
(3) 决定分点.
(4)列频数分布表.
画频数直方图的一般步骤:
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数,该组内的频数为高,画出一个矩形.
小结
时代中学为了了解全校学生参加课外锻炼的情况,抽样调查了50名学生一周内平均每天课外锻炼(单位:min),当抽查到的数据分成5组,下面是尚未完成的频数、频率分布表:
组别 分组 频数(人数) 频率
1 10≤t<20 5
2 20≤t<30
0.22
3 30≤t<40
20
4 40≤t<50
5 50≤t<60
0.04
例1
1、将表中空格处的数据,完成上面的频数、频率分布表;
2、画出相应的频数直方图;
3、这50名学生中,平均每天参加课外锻炼时间不少于30分钟的有多少人?如果该校有2000名学生,估计全校每天参加课外锻炼时间不少于30分钟的人数。
例1
(1)由样本中数据的个数为 50,可求得第 1组的频率为 ,第3组频率为 ; 第2组的频数为 50× 0.22 = 11,第5组的频数为50×0.04=2.
例1
由此可知,第 4组频数为50 -(5+11 + 20+2)= 12,频率为
.将以上数据补入频数、频率分布表,得
例1
组别 分组 频数(人数) 频率
1 10≤t<20 5 0.1
2 20≤t<30
11 0.22
3 30≤t<40
20 0.40
4 40≤t<50
12 0.24
5 50≤t<60
2 0.04
(2)利用(1)中完成的频数分布表,在直角坐标系中画出相应的频数直方图(图6-4).
例1
(3)这50名学生中平均每天参加课外锻炼时间不少于30 min的为第3,4,5组学生,合计为20 +12 +2=34(人),该三组数据的频率为0.68,由此可以估计全校学生平均每天参加课外锻炼时间不少于30 min的约为2 000×0.68=1360(人).
例1
绘制频数直方图的一般步骤:
(1)计算最大值与最小值的差,确定统计量的范围;
(2)决定组数与组距;
(3)确定分点;
(4)列频数分布表;
(5)画频数直方图.
总结
6.3 频数直方图(2)
根据频数直方图解决实际问题.
学习目标
绘制频数分布直方图的一般步骤:
(1)计算最大值与最小值的差,确定统计量的范围;
(2)决定组数与组距;
(3)确定分点;
(4)列频数分布表;
(5)画频数直方图.
回顾
条形统计图可以清楚地表示每个项目的具体数目.
折线统计图可以清楚地反映事物变化的情况.
扇形统计图可以清楚地表示各部分在总体中所占的百分比.
统计图的特点:
九年级一班开展“孝敬父母,帮做家务”的活动,班主任老师统计了全班 50名学生在上周中做家务的时间,并把结果分为如下的 5 组,制作了扇形统计图(图6-5):
例2
A组: 2.5h≤t<3h, B组: 2h≤t < 2.5h,
C组: 1.5h≤t<2h, D组: 1h≤t< 1.5h,
E组:0.5h≤t<1h.
例2
(1) 请按照以上分组列出相应的频数、频率分布表,并画出频数直方图;
解:(1)由题目中的信息,可知共分为 5组,组距为 0.5 h.各组的频率依次为0.04,0.2,0.4,0.3,0.06;总体数据的个数为 50.分别计算出各组的频数,得A组: 50 ×0.04=2;B组: 50 × 0.2=10;C组: 50 × 0.4= 20;D组:50 × 0.3=15; E组: 50 × 0.06=3.由此可以列出频数、频率分布表:
组别 做家务时间 频数 频率
A 2.5≤t<3 2 0.04
B 2≤t<2.5 10 0.2
C 1.5≤t<2 a 0.4
D 1≤t<1.5 b 0.3
E 0.5≤t<1 3 0.06
例2
根据上表,画出频数分布直方图(图6-6).
E
C
D
B
A
做家务时间t/h
0.5
1.5
2
1
2.5
3
0
2
20
15
10
5
3
频数
根据上表,画出频数分布直方图.
例2
(2)估计该班学生在这次活动中做家务的平均时间:
例2
(2) 取各组做家务时间的下限与上限的中间值 (组中值)近似地表示该组学生上周做家务的平均时间.例如取E组数据的上限与下限的平均数 (h )近似地表示E组学生上周做家务的平均时间,从而该班学生平均做家务的时间可按照加权平均数的计算方法,估计为
(3)该班学生上周做家务时间的中位数落在哪个小组内 说明理由.
例2
(3)因为总体数据的个数为 50,且在分组时将 50 个数据(学生做家务时间) 按由大到小的顺序排列,所以该班学生上周做家务时间的中位数是第 25 名学生与第 26名学生做家务时间的平均数,由频数、频率分布表可知,落入A,B 两组的数据个数共2+10 = 12(个),落C组的数据为20个,故中位数应落入C组内.
在上面问题(2)中,如果取该班学生做家务的时间的上、下限的平均数,即
作为全班学生上周做家务的平均时间的估计值,你认为合理吗?为什么?
挑战自我
绘制频数直方图的一般步骤:
(1)计算最大值与最小值的差,确定统计量的范围;
横轴要用组中值(即每个小组两端点数据的中位数) 来代替分组区间
(2)决定组数与组距;
(3)确定分点;
(4)列频数分布表;
(5)画频数直方图.
总结
6.3 频数直方图
1.了解频数直方图的概念;
2.会读频数直方图;
3.会画频数直方图.
学习目标
在统计里,我们称每个考查对象出现的次数为_______,
每个对象出现的次数与总次数的比值为 .
2.各对象的频数之和等于_________,各频率之和等于 .
3.已知一个样本中,50个数据分别落在5个组内,第一、二、
三、五的数据个数分别为2,8,15,5,则第四组的频数为
,频率为 .
频数
频率
数据总和
1
20
40%
回顾
小莹从气象网站上,收集了今年3月上旬某一天我国34个城市的最低气温(单位:°C),如下表所示:
城市 北京 哈尔滨 长春 沈阳 天津 呼和浩特 乌鲁木齐 银川 西宁 兰州 西安 拉萨 成都 重庆 贵阳 昆明 太原
最低
气温(x/°C) 4 -1 -1
-1 4 -7 -3 -1
-4 6 4 0 10 10 10 11 0
观察与思考
城市 石家庄 济南 郑州 合肥 南京 上海 武汉 长沙 南昌 杭州 福州 台北 南宁 海口 广州 香港 澳门
最低
气温(x/°C) 5 7 8 10 10 8 14 15 15 9 15 18 20 22 20 18 18
思考下列问题,并与同学交流:
(1)如何根据表中的信息设计出一个关于上述城市当天最低气温的频数、频率分布表
观察与思考
在上表中,各城市当天最低气温的最大值是22℃,最小值是-7 ℃ ,由此可知,当天最低气温数据的分布范围是
-7 ℃ —22 ℃ ,它们的差为22-(-7)=29 ( ℃ ).
观察与思考
①确定所有数据中最大值与最小值,并计算二者的差.
参照总体中数据的个数是34,数据的最大值与最小值的差是29,可以设定组数为6,由于总体中数据的最大值与最小值的差÷组数=29÷6≈4.8,为了分组方便,可取与4.8最相近的一个整数5作为组距(每组数据的上限与下限的差)于是可把总体数据按以下范围分为6组:
观察与思考
②确定组数、组距,并进行分组.
-7≤x<-2,-2 ≤x <3,3 ≤x <8, 8 ≤x <13,13 ≤x <18,18 ≤x <23.其中-2、3,8,13,18是各组的界限.
利用划记,统计各组中包含的最低气温数据的频数,并计算出相应的频率,填写下面的频数、频率分布表:
观察与思考
③列出相应的频数、频率分布表.
用横轴表示最低气温,纵轴表示频数,
在横轴上先标出各组的上限和下限.由于分
组时各组的组距相等,并且各组的界限既
不重叠又不间断,标注界限时应注意各组
的组距相等,自左向右气温由低到高连续
排列,相邻的两组之间没有间隔.这样就在横轴上标出了首尾相连的6条线段.注意由于这里横轴的原点没有标出,所以纵轴的原点不是横轴的原点.然后分别以各组的上下限为端点的线段为宽、以各组的频数为高,向上分别作6个矩形条,便得到图6-3.
观察与思考
(2)怎样根据列出的频数、频率分布表,制作相应的条形统计图
通过图 6-3,可以直接比较各组的频数的差异,即一个组内城市的个数与另一个组内城市的个数相差几个.
观察与思考
(3)通过观察图6-3,你能得到数据中蕴含的哪些信息 你能看出总体中三月上旬34个城市的最低气温的分布情况吗 与同学交流.
可以看出该天最低气温在8℃~13℃之间的城市最多,有9个城市,而且该组相应的小矩形在直方图的中间位置,这些城市都分布在我国地理纬度的中部地区和西南地区.
像图6-3这样根据频数的分布绘制的条形统计图叫做频数直方图。
将数据进行分组时,组数的多少应适当,组数太少,不能充分显示数据的分布情况;组数太多,不仅繁琐,且容易把性质相近的同类数据分散到各组,从而也不能正确显示数据分布的特征和规律。
一般的,数据在100个以内,可按情况分为5~12组。
加油站
像这样,根据频数的分布绘制的条形统计图叫做频数直方图.
边界值
组中值
定义:
(1) 计算极差
(2) 决定组距与组数.
(3) 决定分点.
(4)列频数分布表.
画频数直方图的一般步骤:
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数,该组内的频数为高,画出一个矩形.
小结
时代中学为了了解全校学生参加课外锻炼的情况,抽样调查了50名学生一周内平均每天课外锻炼(单位:min),当抽查到的数据分成5组,下面是尚未完成的频数、频率分布表:
组别 分组 频数(人数) 频率
1 10≤t<20 5
2 20≤t<30
0.22
3 30≤t<40
20
4 40≤t<50
5 50≤t<60
0.04
例1
1、将表中空格处的数据,完成上面的频数、频率分布表;
2、画出相应的频数直方图;
3、这50名学生中,平均每天参加课外锻炼时间不少于30分钟的有多少人?如果该校有2000名学生,估计全校每天参加课外锻炼时间不少于30分钟的人数。
例1
(1)由样本中数据的个数为 50,可求得第 1组的频率为 ,第3组频率为 ; 第2组的频数为 50× 0.22 = 11,第5组的频数为50×0.04=2.
例1
由此可知,第 4组频数为50 -(5+11 + 20+2)= 12,频率为
.将以上数据补入频数、频率分布表,得
例1
组别 分组 频数(人数) 频率
1 10≤t<20 5 0.1
2 20≤t<30
11 0.22
3 30≤t<40
20 0.40
4 40≤t<50
12 0.24
5 50≤t<60
2 0.04
(2)利用(1)中完成的频数分布表,在直角坐标系中画出相应的频数直方图(图6-4).
例1
(3)这50名学生中平均每天参加课外锻炼时间不少于30 min的为第3,4,5组学生,合计为20 +12 +2=34(人),该三组数据的频率为0.68,由此可以估计全校学生平均每天参加课外锻炼时间不少于30 min的约为2 000×0.68=1360(人).
例1
绘制频数直方图的一般步骤:
(1)计算最大值与最小值的差,确定统计量的范围;
(2)决定组数与组距;
(3)确定分点;
(4)列频数分布表;
(5)画频数直方图.
总结
6.3 频数直方图(2)
根据频数直方图解决实际问题.
学习目标
绘制频数分布直方图的一般步骤:
(1)计算最大值与最小值的差,确定统计量的范围;
(2)决定组数与组距;
(3)确定分点;
(4)列频数分布表;
(5)画频数直方图.
回顾
条形统计图可以清楚地表示每个项目的具体数目.
折线统计图可以清楚地反映事物变化的情况.
扇形统计图可以清楚地表示各部分在总体中所占的百分比.
统计图的特点:
九年级一班开展“孝敬父母,帮做家务”的活动,班主任老师统计了全班 50名学生在上周中做家务的时间,并把结果分为如下的 5 组,制作了扇形统计图(图6-5):
例2
A组: 2.5h≤t<3h, B组: 2h≤t < 2.5h,
C组: 1.5h≤t<2h, D组: 1h≤t< 1.5h,
E组:0.5h≤t<1h.
例2
(1) 请按照以上分组列出相应的频数、频率分布表,并画出频数直方图;
解:(1)由题目中的信息,可知共分为 5组,组距为 0.5 h.各组的频率依次为0.04,0.2,0.4,0.3,0.06;总体数据的个数为 50.分别计算出各组的频数,得A组: 50 ×0.04=2;B组: 50 × 0.2=10;C组: 50 × 0.4= 20;D组:50 × 0.3=15; E组: 50 × 0.06=3.由此可以列出频数、频率分布表:
组别 做家务时间 频数 频率
A 2.5≤t<3 2 0.04
B 2≤t<2.5 10 0.2
C 1.5≤t<2 a 0.4
D 1≤t<1.5 b 0.3
E 0.5≤t<1 3 0.06
例2
根据上表,画出频数分布直方图(图6-6).
E
C
D
B
A
做家务时间t/h
0.5
1.5
2
1
2.5
3
0
2
20
15
10
5
3
频数
根据上表,画出频数分布直方图.
例2
(2)估计该班学生在这次活动中做家务的平均时间:
例2
(2) 取各组做家务时间的下限与上限的中间值 (组中值)近似地表示该组学生上周做家务的平均时间.例如取E组数据的上限与下限的平均数 (h )近似地表示E组学生上周做家务的平均时间,从而该班学生平均做家务的时间可按照加权平均数的计算方法,估计为
(3)该班学生上周做家务时间的中位数落在哪个小组内 说明理由.
例2
(3)因为总体数据的个数为 50,且在分组时将 50 个数据(学生做家务时间) 按由大到小的顺序排列,所以该班学生上周做家务时间的中位数是第 25 名学生与第 26名学生做家务时间的平均数,由频数、频率分布表可知,落入A,B 两组的数据个数共2+10 = 12(个),落C组的数据为20个,故中位数应落入C组内.
在上面问题(2)中,如果取该班学生做家务的时间的上、下限的平均数,即
作为全班学生上周做家务的平均时间的估计值,你认为合理吗?为什么?
挑战自我
绘制频数直方图的一般步骤:
(1)计算最大值与最小值的差,确定统计量的范围;
横轴要用组中值(即每个小组两端点数据的中位数) 来代替分组区间
(2)决定组数与组距;
(3)确定分点;
(4)列频数分布表;
(5)画频数直方图.
总结
