人教版八年级下册第十九章 一次函数19.3课题学习选择方案同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册第十九章 一次函数19.3课题学习选择方案同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 461.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 11:40:54 | ||
图片预览


文档简介
19.3课题学习选择方案 同步练习
一、单选题
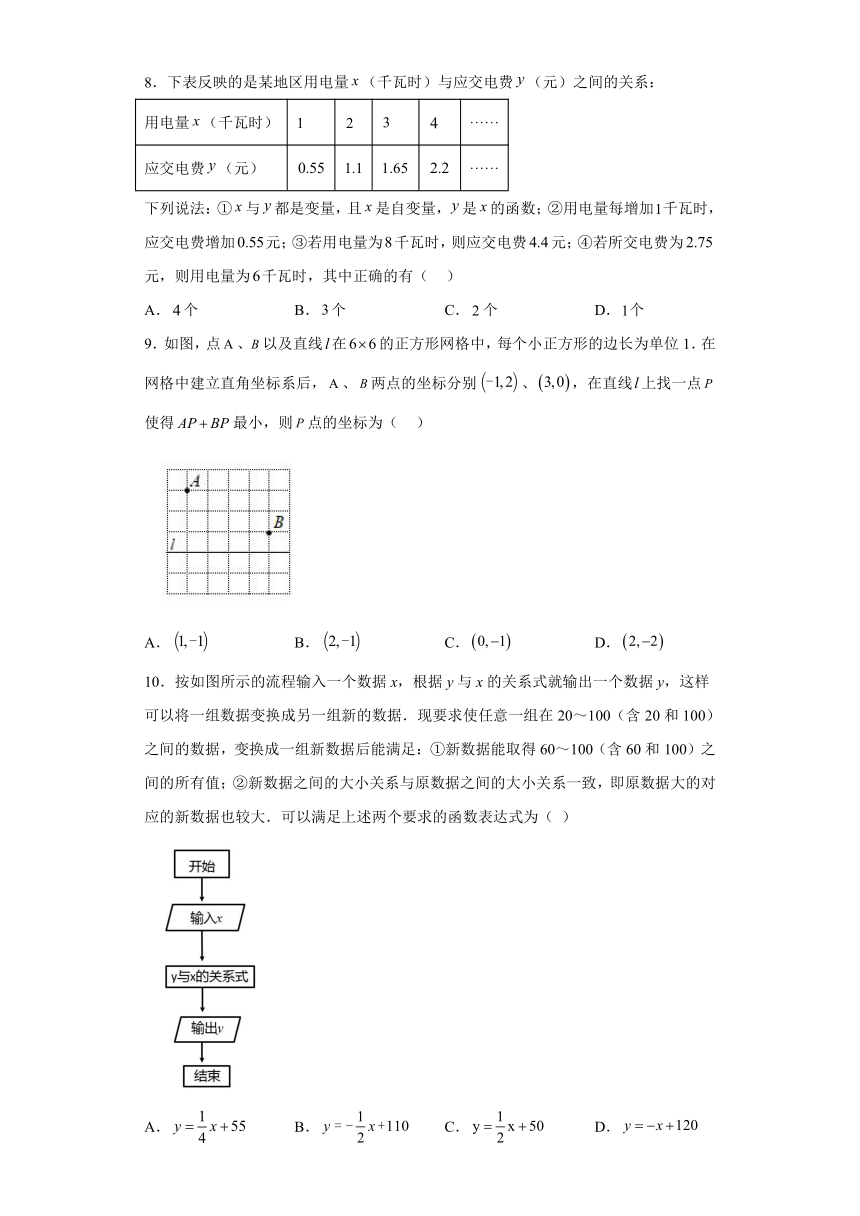
1.甲乙两车沿着公路从A地前往B地,汽车离开A地的距离y(km)与时间t(h)的对应的关系如图所示.则下列结论错误的是( )
A.甲车的平均速度为60km/h. B.乙车的平均速度为100km/h.
C.甲乙两车在10:00时相遇. D.乙比甲车先到达B地.
2.直线与x轴的交点是,则k的值是( )
A.3 B.2 C. D.
3.如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
4.在某一阶段,某商品的销售量与销售价之间存在如下关系:设该商品的销售价为x元,售量为y件,估计当x=137时,y的值可能为( )
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
A.63 B.59 C.53 D.43
5.某网约车计费办法如图所示根据图象信息,下列说法正确的是( )
A.该网约车起步价是12元
B.在3千米内只收12元
C.超过3千米(x>3)部分每千米收费3元
D.超过3千米(x>3)时所需费用y与x之间的函数关系式是y=2x+4
6.网语期印,李明同学在老家学习生活,为缓解线上学习疲劳,在某个周末和爸爸进行登山锻炼,登山过程中,两人距地面的高度y(米)与登山时间x(分钟)之间的函数图像如图所示(甲为爸爸,乙为李明),李明提速后,李明的登山速度是原来速度的2倍,并先到达山顶.根据图象所提供的信息,下列说法情误的是( )
A.甲登山的速度是每分钟米
B.乙在A地时距地面的高度b为米
C.乙登山分钟时追上甲
D.登山时间为5分钟、8分钟、分钟时,甲、乙两人距地面的高度差为米
7.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示应为图中的( )
A. B.
C. D.
8.下表反映的是某地区用电量(千瓦时)与应交电费(元)之间的关系:
用电量(千瓦时) ······
应交电费(元) ······
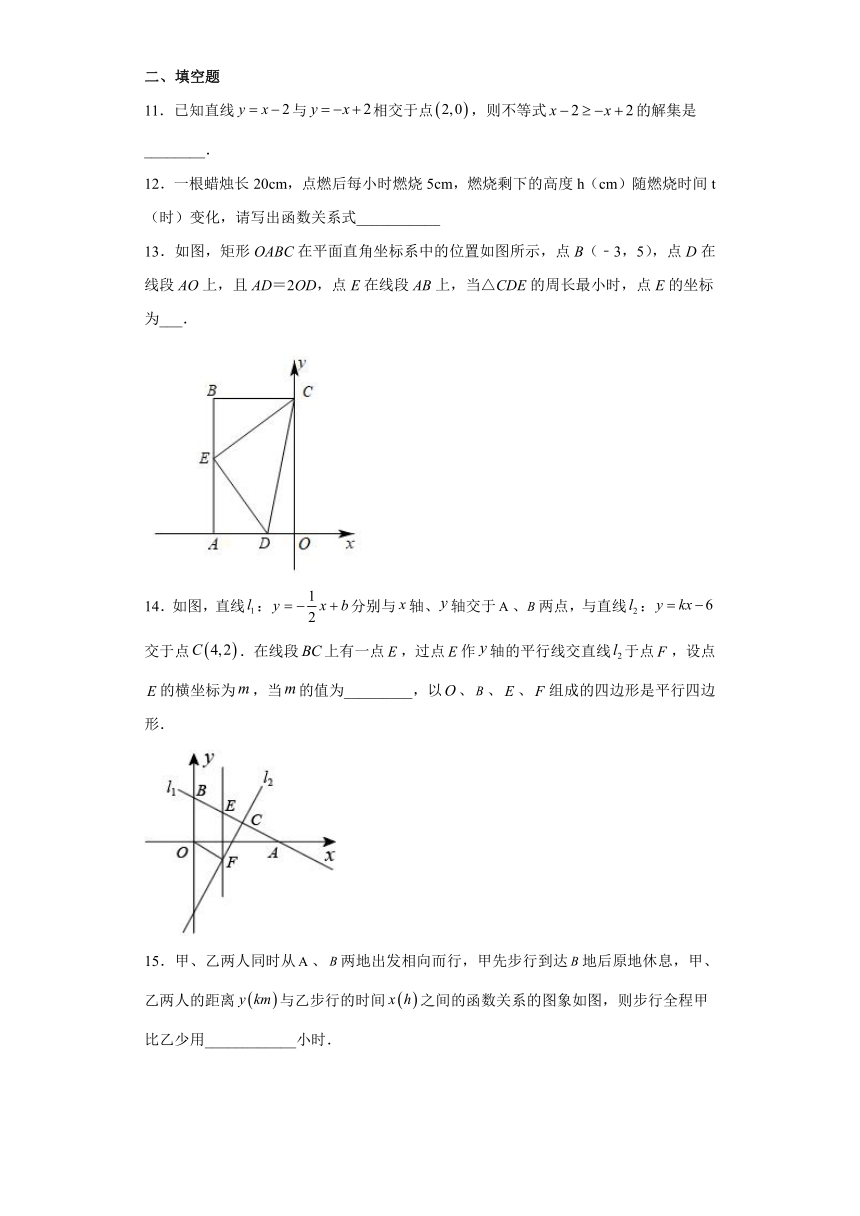
下列说法:①与都是变量,且是自变量,是的函数;②用电量每增加千瓦时,应交电费增加元;③若用电量为千瓦时,则应交电费元;④若所交电费为元,则用电量为千瓦时,其中正确的有( )
A.个 B.个 C.个 D.个
9.如图,点、以及直线在的正方形网格中,每个小正方形的边长为单位1.在网格中建立直角坐标系后,、两点的坐标分别、,在直线上找一点使得最小,则点的坐标为( )
A. B. C. D.
10.按如图所示的流程输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据.现要求使任意一组在20~100(含20和100)之间的数据,变换成一组新数据后能满足:①新数据能取得60~100(含60和100)之间的所有值;②新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大.可以满足上述两个要求的函数表达式为( )
A. B. C. D.
二、填空题
11.已知直线与相交于点,则不等式的解集是________.
12.一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧剩下的高度h(cm)随燃烧时间t(时)变化,请写出函数关系式___________
13.如图,矩形OABC在平面直角坐标系中的位置如图所示,点B(﹣3,5),点D在线段AO上,且AD=2OD,点E在线段AB上,当△CDE的周长最小时,点E的坐标为___.
14.如图,直线:分别与轴、轴交于、两点,与直线:交于点.在线段上有一点,过点作轴的平行线交直线于点,设点的横坐标为,当的值为_________,以、、、组成的四边形是平行四边形.
15.甲、乙两人同时从、两地出发相向而行,甲先步行到达地后原地休息,甲、乙两人的距离与乙步行的时间之间的函数关系的图象如图,则步行全程甲比乙少用____________小时.
三、解答题
16.甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入,两队合作完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系.求甲、乙两队合作完成剩下的全部工程时,工作量y与天数x间的函数关系式.
17.绍兴首条智慧快速路于今年3月19日正式通车.该快速路上,两站相距,甲、乙两名杭州亚运会会务工作志愿者从站出发前往站附近的比赛场馆开展服务.甲乘坐无人驾驶小巴,乙乘坐无人驾驶汽车.图中,分别表示甲、乙离开站的路程与时间的函数关系的图象.
(1)填空:甲比乙提前______分钟出发;无人驾驶小巴的速度为______;当乙乘坐无人驾驶汽车到达站时,无人驾驶小巴离站还有______.
(2)求乙离开站的路程与时间的函数关系式并说明图中两函数图象交点的实际意义.
18.某商场计划投入一笔资金采购一批紧俏商品,经市场调研发现,如果本月初出售,可获利10%,然后将本利再投资其他商品,到下月初又可获利10%;如果下月初出售可获利25%,但要支付仓储费8000元.设商场投入资金x元,请你根据商场的资金情况,向商场提出合理化建议,说明何时出售获利较多.
19.某医药公司把一批药品运往外地,现有两种运输方式可供选择.
方式一:使用快递公司的邮车运输,装卸收费400元,另外每千米再加收4元;
方式二:使用快递公司的火车运输,装卸收费820元,另外每千米再加收2元.
(1)请你分别写出邮车、火车运输的总费用y1(元),y2(元)与路程x(km)之间的函数解析式;
(2)你认为选用哪种运输方式较好,为什么?
20.为弘扬雷锋精神,重温革命先烈的艰苦奋斗历史,某校组织九年级全体师生前往雷锋纪念馆参观,需要租用甲、乙两种客车共辆(每种车至少租一辆).已知甲、乙两种客车的租金分别为元辆和元辆,设租用乙种客车辆,租车费用为元.
(1)求与之间的函数关系式;
(2)若租用乙种客车的数量少于甲种客车的数量,租用乙种客车多少辆时,租车费用最少?最少费用是多少元?
参考答案
1.C
2.D
3.B
4.D
5.D
6.C
7.D
8.B
9.B
10.C
11.
12.h=-5t+20/h=20-5t
13.(﹣3,2)
14.
15.1.75
16.
17.(1)5;;
(2)(),实际意义见解析
18.解:设如果商场本月初出售,下月初可获利y1元,
则y1=10%x+(1+10%)x·10%=0.1x+0.11x=0.21x,
设如果商场下月初出售,可获利y2元,则y2=25%x-8 000=0.25x-8 000,
当y1=y2时,0.21x=0.25x-8 000,解得x=200 000,
所以若商场投入资金为20万元,两种出售方式获利相同;若商场投入资金少于20万元,本月初出售获利较多;若商场投入资金多于20万元,下月初出售获利较多.
19.(1)由题意得:y1=4x+400,y2=2x+820;
(2) y1=y2时,4x+400=2x+820,解得x=210;
y1>y2时,4x+400>2x+820,解得x>210,
y1<y2时,4x+400<2x+820,解得x<210,
所以当运输路程小于210 km时,y1当运输的路程等于210 km时,y1=y2,两种方式一样;
当运输路程大于210 km时,y1>y2,选择火车运输较好.
20.(1)解:设租用乙种客车辆,租车费用为元,依题意得:
,
整理得:.
(2)解:∵租用乙种客车的数量少于甲种客车的数量,
,即
或,
当时,,
当时,,
故租用乙种客车辆时,租车费用最少,为元.
答:租用乙种客车辆时,租车费用最少,为元.
一、单选题
1.甲乙两车沿着公路从A地前往B地,汽车离开A地的距离y(km)与时间t(h)的对应的关系如图所示.则下列结论错误的是( )
A.甲车的平均速度为60km/h. B.乙车的平均速度为100km/h.
C.甲乙两车在10:00时相遇. D.乙比甲车先到达B地.
2.直线与x轴的交点是,则k的值是( )
A.3 B.2 C. D.
3.如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
4.在某一阶段,某商品的销售量与销售价之间存在如下关系:设该商品的销售价为x元,售量为y件,估计当x=137时,y的值可能为( )
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
A.63 B.59 C.53 D.43
5.某网约车计费办法如图所示根据图象信息,下列说法正确的是( )
A.该网约车起步价是12元
B.在3千米内只收12元
C.超过3千米(x>3)部分每千米收费3元
D.超过3千米(x>3)时所需费用y与x之间的函数关系式是y=2x+4
6.网语期印,李明同学在老家学习生活,为缓解线上学习疲劳,在某个周末和爸爸进行登山锻炼,登山过程中,两人距地面的高度y(米)与登山时间x(分钟)之间的函数图像如图所示(甲为爸爸,乙为李明),李明提速后,李明的登山速度是原来速度的2倍,并先到达山顶.根据图象所提供的信息,下列说法情误的是( )
A.甲登山的速度是每分钟米
B.乙在A地时距地面的高度b为米
C.乙登山分钟时追上甲
D.登山时间为5分钟、8分钟、分钟时,甲、乙两人距地面的高度差为米
7.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示应为图中的( )
A. B.
C. D.
8.下表反映的是某地区用电量(千瓦时)与应交电费(元)之间的关系:
用电量(千瓦时) ······
应交电费(元) ······
下列说法:①与都是变量,且是自变量,是的函数;②用电量每增加千瓦时,应交电费增加元;③若用电量为千瓦时,则应交电费元;④若所交电费为元,则用电量为千瓦时,其中正确的有( )
A.个 B.个 C.个 D.个
9.如图,点、以及直线在的正方形网格中,每个小正方形的边长为单位1.在网格中建立直角坐标系后,、两点的坐标分别、,在直线上找一点使得最小,则点的坐标为( )
A. B. C. D.
10.按如图所示的流程输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据.现要求使任意一组在20~100(含20和100)之间的数据,变换成一组新数据后能满足:①新数据能取得60~100(含60和100)之间的所有值;②新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大.可以满足上述两个要求的函数表达式为( )
A. B. C. D.
二、填空题
11.已知直线与相交于点,则不等式的解集是________.
12.一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧剩下的高度h(cm)随燃烧时间t(时)变化,请写出函数关系式___________
13.如图,矩形OABC在平面直角坐标系中的位置如图所示,点B(﹣3,5),点D在线段AO上,且AD=2OD,点E在线段AB上,当△CDE的周长最小时,点E的坐标为___.
14.如图,直线:分别与轴、轴交于、两点,与直线:交于点.在线段上有一点,过点作轴的平行线交直线于点,设点的横坐标为,当的值为_________,以、、、组成的四边形是平行四边形.
15.甲、乙两人同时从、两地出发相向而行,甲先步行到达地后原地休息,甲、乙两人的距离与乙步行的时间之间的函数关系的图象如图,则步行全程甲比乙少用____________小时.
三、解答题
16.甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入,两队合作完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系.求甲、乙两队合作完成剩下的全部工程时,工作量y与天数x间的函数关系式.
17.绍兴首条智慧快速路于今年3月19日正式通车.该快速路上,两站相距,甲、乙两名杭州亚运会会务工作志愿者从站出发前往站附近的比赛场馆开展服务.甲乘坐无人驾驶小巴,乙乘坐无人驾驶汽车.图中,分别表示甲、乙离开站的路程与时间的函数关系的图象.
(1)填空:甲比乙提前______分钟出发;无人驾驶小巴的速度为______;当乙乘坐无人驾驶汽车到达站时,无人驾驶小巴离站还有______.
(2)求乙离开站的路程与时间的函数关系式并说明图中两函数图象交点的实际意义.
18.某商场计划投入一笔资金采购一批紧俏商品,经市场调研发现,如果本月初出售,可获利10%,然后将本利再投资其他商品,到下月初又可获利10%;如果下月初出售可获利25%,但要支付仓储费8000元.设商场投入资金x元,请你根据商场的资金情况,向商场提出合理化建议,说明何时出售获利较多.
19.某医药公司把一批药品运往外地,现有两种运输方式可供选择.
方式一:使用快递公司的邮车运输,装卸收费400元,另外每千米再加收4元;
方式二:使用快递公司的火车运输,装卸收费820元,另外每千米再加收2元.
(1)请你分别写出邮车、火车运输的总费用y1(元),y2(元)与路程x(km)之间的函数解析式;
(2)你认为选用哪种运输方式较好,为什么?
20.为弘扬雷锋精神,重温革命先烈的艰苦奋斗历史,某校组织九年级全体师生前往雷锋纪念馆参观,需要租用甲、乙两种客车共辆(每种车至少租一辆).已知甲、乙两种客车的租金分别为元辆和元辆,设租用乙种客车辆,租车费用为元.
(1)求与之间的函数关系式;
(2)若租用乙种客车的数量少于甲种客车的数量,租用乙种客车多少辆时,租车费用最少?最少费用是多少元?
参考答案
1.C
2.D
3.B
4.D
5.D
6.C
7.D
8.B
9.B
10.C
11.
12.h=-5t+20/h=20-5t
13.(﹣3,2)
14.
15.1.75
16.
17.(1)5;;
(2)(),实际意义见解析
18.解:设如果商场本月初出售,下月初可获利y1元,
则y1=10%x+(1+10%)x·10%=0.1x+0.11x=0.21x,
设如果商场下月初出售,可获利y2元,则y2=25%x-8 000=0.25x-8 000,
当y1=y2时,0.21x=0.25x-8 000,解得x=200 000,
所以若商场投入资金为20万元,两种出售方式获利相同;若商场投入资金少于20万元,本月初出售获利较多;若商场投入资金多于20万元,下月初出售获利较多.
19.(1)由题意得:y1=4x+400,y2=2x+820;
(2) y1=y2时,4x+400=2x+820,解得x=210;
y1>y2时,4x+400>2x+820,解得x>210,
y1<y2时,4x+400<2x+820,解得x<210,
所以当运输路程小于210 km时,y1
当运输路程大于210 km时,y1>y2,选择火车运输较好.
20.(1)解:设租用乙种客车辆,租车费用为元,依题意得:
,
整理得:.
(2)解:∵租用乙种客车的数量少于甲种客车的数量,
,即
或,
当时,,
当时,,
故租用乙种客车辆时,租车费用最少,为元.
答:租用乙种客车辆时,租车费用最少,为元.
