山东省济南市莱芜区陈毅中学片区联盟2022-2023学年七年级下学期期中考试数学试题(含答案)
文档属性
| 名称 | 山东省济南市莱芜区陈毅中学片区联盟2022-2023学年七年级下学期期中考试数学试题(含答案) |
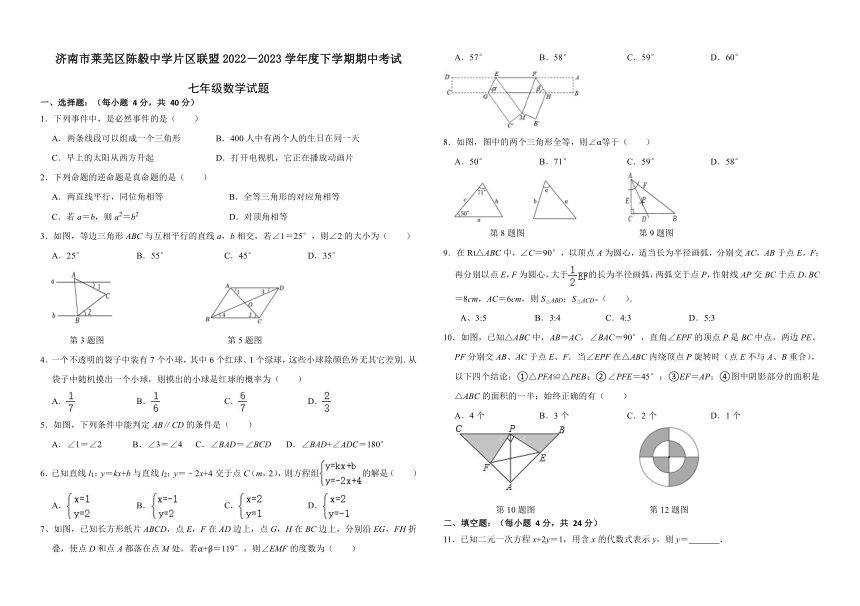
|
|
| 格式 | doc | ||
| 文件大小 | 257.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-13 00:00:00 | ||
图片预览



文档简介
济南市莱芜区陈毅中学片区联盟2022-2023学年度下学期期中考试
七年级数学试题
选择题:(每小题 4分,共 40分)
1.下列事件中,是必然事件的是( )
A.两条线段可以组成一个三角形 B.400人中有两个人的生日在同一天
C.早上的太阳从西方升起 D.打开电视机,它正在播放动画片
2.下列命题的逆命题是真命题的是( )
A.两直线平行,同位角相等 B.全等三角形的对应角相等
C.若a=b,则a2=b2 D.对顶角相等
3.如图,等边三角形ABC与互相平行的直线a,b相交,若∠1=25°,则∠2的大小为( )
A.25° B.55° C.45° D.35°
第3题图 第5题图
4.一个不透明的袋子中装有7个小球,其中6个红球、1个绿球,这些小球除颜色外无其它差别.从袋子中随机摸出一个小球,则摸出的小球是红球的概率为( )
A. B. C. D.
5.如图,下列条件中能判定AB∥CD的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠BAD=∠BCD D.∠BAD+∠ADC=180°
6.已知直线l1:y=kx+b与直线l2:y=﹣2x+4交于点C(m,2),则方程组的解是( )
A. B. C. D.
7、如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )
A.57° B.58° C.59° D.60°
8.如图,图中的两个三角形全等,则∠α等于( )
A.50° B.71° C.59° D.58°
第8题图 第9题图
在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点E,F;再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交BC于点D.BC=8cm,AC=6cm,则S△ABD:S△ACD=( ).
A、3:5 B.3:4 C.4:3 D.5:3
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),以下四个结论:①△PFA≌△PEB;②∠PFE=45°;③EF=AP;④图中阴影部分的面积是△ABC的面积的一半;始终正确的有( )
A.4个 B.3个 C.2个 D.1个
第10题图 第12题图
填空题:(每小题 4分,共 24分)
11.已知二元一次方程x+2y=1,用含x的代数式表示y,则y= .
12.如图,过圆心且互相垂直的两条直线将两个同心圆分成了若干部分,在该图形区域内任取一点,则该点取自阴影部分的概率是 .
13.如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,连接AE,AF,若BC=20,则△AEF的周长是
14.若是方程3x+y=1的一个解,则9a+3b+2023= .
15.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为18和21两个部分,则这个等腰三角形的底边长为 .
16.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,……,An﹣1Bn﹣1=An﹣1An(n≥2且n为整数),若∠B=48°,则∠A2022A2023B2022的度数为 .
三、解答题:
17.(6分)解方程组:
18.(6分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2.求证:△AEC≌△BED.
19.(6分)一个不透明的盒子里装有15张红色卡片,20张黄色卡片,12张蓝色卡片和若干张黑色卡片,每张卡片除颜色外都相同,从中任意摸出一张卡片,摸到红色卡片的概率是0.25.
(1)从中任意摸出一张卡片,摸到蓝色卡片的概率是多少?
(2)求盒子里黑色卡片的个数.
20.(8分)如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F. (1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
第20题图 第22题图
21.(8分)已知方程组与方程组的解相等,试求3a+b的值.
22.(8分) 如图:△ABE和△ACF为等腰直角三角形,连接EC、BF,试说明EC、BF有怎样的关系?试证明你的结论.
23.(10分)仔细阅读下面解方程组的方法,然后解决有关问题:
解方程组时,如果直接消元,那将时很繁琐的,若采用下面的解法,则会简单很多.
解:①﹣②,得:2x+2y=2,即x+y=1 ③
③×16,得:16x+16y=16 ④
②﹣④,得:x=﹣1
将x=﹣1
代入③得:y=2
∴方程组的解为:
(1)请你采用上述方法解方程组:
(2)请你采用上述方法解关于x,y的方程组.
24.(10分)新冠疫情期间,我市中学生积极行动起来,每人拿出自己一天的零花钱,筹款为贫困地区捐赠了19吨消毒液,并将消毒液运往该区.已知用3辆A型车和1辆B型车装满货物一次可运货9吨;用1辆A型车和2辆B型车装满货物一次可运货8吨.计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满消毒液.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满消毒液一次可分别运送多少吨?
(2)请你帮我们设计租车方案;
(3)若1辆A型车需租金90元/次,1辆B型车需租金110元/次.请选出最省钱的租车方案,并求出最少租车费.
25.(12分)如图所示,直线l1的函数表达式为y=3x﹣2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(1)求点D和点C的坐标;
(2)求直线l2的函数表达式;
(3)求两直线与x轴围成的三角形面积.
26.(12分)问题背景:(1)如图①,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,请直接写出BD、CE、DE的数量关系.
拓展延伸:(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC请写出DE、BD、CE三条线段的数量关系,并说明理由.
实际应用:(3)如图③,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求B点的坐标.
七年级数学答案
一、选择题(每小题 4分,共 40分)
1 2 3 4 5 6 7 8 9 10
B A D C D A B C D B
填空题(每小题 4分,共24分)
11、y=- x+ 12、 13、20 14、 2026 15、11或15 16、()2022×66°
三.解答题(共1小题)
17、,
整理得:,
②×2得:4m+2n=28③,
①+③得:7m=70,
解得:m=10,
把m=10代入②得:20+n=14,
解得:n=﹣6,
故原方程组的解是:.
18、证法一,证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
20、(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=72°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=48°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣48°=42°.
21、解:由已知可得,解得,
把代入剩下的两个方程组成的方程组,
得,
解得.
故a、b的值为
所以3a+b=5
22、(1)解:结论:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAF.
在△EAC和△BAF中,
,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
∴EC=BF,EC⊥BF.
解:(1),
①﹣②,得:2x+2y=2,即x+y=1 ③
③×2011,得:2011x+2011y=2011④
②﹣④,得:x=﹣1,
将x=﹣1代入③得:y=2,
∴方程组的解为:;
(2)
解:①﹣②,得:(a﹣b)x+(a﹣b)y=a﹣b,
∵a≠b,
∴x+y=1 ③
③×(b+1),得:(b+1)x+(b+1)y=b+1④
②﹣④,得:x=﹣1,
将x=﹣1代入③得:y=2,
∴方程组的解为:.
24、解:(1)设1辆A型车载满消毒液一次可运送x吨,1辆B型车载满消毒液一次可运送y吨,
依题意得:,
解得:.
答:1辆A型车载满消毒液一次可运送2吨,1辆B型车载满消毒液一次可运送3吨.
(2)依题意得:2a+3b=19,
∴a=.
又∵a,b均为整数,
∴或或,
∴共有3种租车方案,
方案1:租用A型车8辆,B型车1辆;
方案2:租用A型车5辆,B型车3辆;
方案3:租用A型车2辆,B型车5辆.
(3)选用方案1所需租车费为90×8+110×1=830(元);
选用方案2所需租车费为90×5+110×3=780(元);
选用方案3所需租车费为90×2+110×5=730(元).
∵830>780>730,
25、解:(1)在y=3x﹣2中
令y=0,即3x﹣2=0 解得x=,
∴D(,0),
∵点C(m,3)在直线y=3x﹣2上,
∴3m﹣2=3,
∴m=,
∴C(,3);
(2)设直线l2的函数表达式为y=kx+b(k≠0),
由题意得:,
解得,
∴l2的函数表达式为y=﹣x+;
(3)易知A( ,0)
∴AD=﹣=,
∴S△ADC=×3×0.5=.
26、(1)证明:∵BD⊥AD,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠CAE+∠BAD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴AE=BD,AD=CE,
∴DE=AD+AE=BD+CE;
(2)解:DE=BD+CE,
理由如下:在△ABD中,∠ABD=180°﹣∠ADB﹣∠BAD,
∵∠CAE=180°﹣∠BAC﹣∠BAD,∠BDA=∠BAC,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴AE=BD,AD=CE,
∴DE=AD+AE=BD+CE;
(3)解:如图③,作AE⊥x轴于E,BF⊥x轴于F,
由(1)可知,△AEC≌△CFB,
∴CF=AE=3,BF=CE=OE﹣OC=4,
∴OF=CF﹣OC=1,
∴点B的坐标为(1,4).
七年级数学试题
选择题:(每小题 4分,共 40分)
1.下列事件中,是必然事件的是( )
A.两条线段可以组成一个三角形 B.400人中有两个人的生日在同一天
C.早上的太阳从西方升起 D.打开电视机,它正在播放动画片
2.下列命题的逆命题是真命题的是( )
A.两直线平行,同位角相等 B.全等三角形的对应角相等
C.若a=b,则a2=b2 D.对顶角相等
3.如图,等边三角形ABC与互相平行的直线a,b相交,若∠1=25°,则∠2的大小为( )
A.25° B.55° C.45° D.35°
第3题图 第5题图
4.一个不透明的袋子中装有7个小球,其中6个红球、1个绿球,这些小球除颜色外无其它差别.从袋子中随机摸出一个小球,则摸出的小球是红球的概率为( )
A. B. C. D.
5.如图,下列条件中能判定AB∥CD的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠BAD=∠BCD D.∠BAD+∠ADC=180°
6.已知直线l1:y=kx+b与直线l2:y=﹣2x+4交于点C(m,2),则方程组的解是( )
A. B. C. D.
7、如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )
A.57° B.58° C.59° D.60°
8.如图,图中的两个三角形全等,则∠α等于( )
A.50° B.71° C.59° D.58°
第8题图 第9题图
在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点E,F;再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交BC于点D.BC=8cm,AC=6cm,则S△ABD:S△ACD=( ).
A、3:5 B.3:4 C.4:3 D.5:3
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),以下四个结论:①△PFA≌△PEB;②∠PFE=45°;③EF=AP;④图中阴影部分的面积是△ABC的面积的一半;始终正确的有( )
A.4个 B.3个 C.2个 D.1个
第10题图 第12题图
填空题:(每小题 4分,共 24分)
11.已知二元一次方程x+2y=1,用含x的代数式表示y,则y= .
12.如图,过圆心且互相垂直的两条直线将两个同心圆分成了若干部分,在该图形区域内任取一点,则该点取自阴影部分的概率是 .
13.如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,连接AE,AF,若BC=20,则△AEF的周长是
14.若是方程3x+y=1的一个解,则9a+3b+2023= .
15.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为18和21两个部分,则这个等腰三角形的底边长为 .
16.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,……,An﹣1Bn﹣1=An﹣1An(n≥2且n为整数),若∠B=48°,则∠A2022A2023B2022的度数为 .
三、解答题:
17.(6分)解方程组:
18.(6分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2.求证:△AEC≌△BED.
19.(6分)一个不透明的盒子里装有15张红色卡片,20张黄色卡片,12张蓝色卡片和若干张黑色卡片,每张卡片除颜色外都相同,从中任意摸出一张卡片,摸到红色卡片的概率是0.25.
(1)从中任意摸出一张卡片,摸到蓝色卡片的概率是多少?
(2)求盒子里黑色卡片的个数.
20.(8分)如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F. (1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
第20题图 第22题图
21.(8分)已知方程组与方程组的解相等,试求3a+b的值.
22.(8分) 如图:△ABE和△ACF为等腰直角三角形,连接EC、BF,试说明EC、BF有怎样的关系?试证明你的结论.
23.(10分)仔细阅读下面解方程组的方法,然后解决有关问题:
解方程组时,如果直接消元,那将时很繁琐的,若采用下面的解法,则会简单很多.
解:①﹣②,得:2x+2y=2,即x+y=1 ③
③×16,得:16x+16y=16 ④
②﹣④,得:x=﹣1
将x=﹣1
代入③得:y=2
∴方程组的解为:
(1)请你采用上述方法解方程组:
(2)请你采用上述方法解关于x,y的方程组.
24.(10分)新冠疫情期间,我市中学生积极行动起来,每人拿出自己一天的零花钱,筹款为贫困地区捐赠了19吨消毒液,并将消毒液运往该区.已知用3辆A型车和1辆B型车装满货物一次可运货9吨;用1辆A型车和2辆B型车装满货物一次可运货8吨.计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满消毒液.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满消毒液一次可分别运送多少吨?
(2)请你帮我们设计租车方案;
(3)若1辆A型车需租金90元/次,1辆B型车需租金110元/次.请选出最省钱的租车方案,并求出最少租车费.
25.(12分)如图所示,直线l1的函数表达式为y=3x﹣2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(1)求点D和点C的坐标;
(2)求直线l2的函数表达式;
(3)求两直线与x轴围成的三角形面积.
26.(12分)问题背景:(1)如图①,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,请直接写出BD、CE、DE的数量关系.
拓展延伸:(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC请写出DE、BD、CE三条线段的数量关系,并说明理由.
实际应用:(3)如图③,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求B点的坐标.
七年级数学答案
一、选择题(每小题 4分,共 40分)
1 2 3 4 5 6 7 8 9 10
B A D C D A B C D B
填空题(每小题 4分,共24分)
11、y=- x+ 12、 13、20 14、 2026 15、11或15 16、()2022×66°
三.解答题(共1小题)
17、,
整理得:,
②×2得:4m+2n=28③,
①+③得:7m=70,
解得:m=10,
把m=10代入②得:20+n=14,
解得:n=﹣6,
故原方程组的解是:.
18、证法一,证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
20、(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=72°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=48°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣48°=42°.
21、解:由已知可得,解得,
把代入剩下的两个方程组成的方程组,
得,
解得.
故a、b的值为
所以3a+b=5
22、(1)解:结论:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAF.
在△EAC和△BAF中,
,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
∴EC=BF,EC⊥BF.
解:(1),
①﹣②,得:2x+2y=2,即x+y=1 ③
③×2011,得:2011x+2011y=2011④
②﹣④,得:x=﹣1,
将x=﹣1代入③得:y=2,
∴方程组的解为:;
(2)
解:①﹣②,得:(a﹣b)x+(a﹣b)y=a﹣b,
∵a≠b,
∴x+y=1 ③
③×(b+1),得:(b+1)x+(b+1)y=b+1④
②﹣④,得:x=﹣1,
将x=﹣1代入③得:y=2,
∴方程组的解为:.
24、解:(1)设1辆A型车载满消毒液一次可运送x吨,1辆B型车载满消毒液一次可运送y吨,
依题意得:,
解得:.
答:1辆A型车载满消毒液一次可运送2吨,1辆B型车载满消毒液一次可运送3吨.
(2)依题意得:2a+3b=19,
∴a=.
又∵a,b均为整数,
∴或或,
∴共有3种租车方案,
方案1:租用A型车8辆,B型车1辆;
方案2:租用A型车5辆,B型车3辆;
方案3:租用A型车2辆,B型车5辆.
(3)选用方案1所需租车费为90×8+110×1=830(元);
选用方案2所需租车费为90×5+110×3=780(元);
选用方案3所需租车费为90×2+110×5=730(元).
∵830>780>730,
25、解:(1)在y=3x﹣2中
令y=0,即3x﹣2=0 解得x=,
∴D(,0),
∵点C(m,3)在直线y=3x﹣2上,
∴3m﹣2=3,
∴m=,
∴C(,3);
(2)设直线l2的函数表达式为y=kx+b(k≠0),
由题意得:,
解得,
∴l2的函数表达式为y=﹣x+;
(3)易知A( ,0)
∴AD=﹣=,
∴S△ADC=×3×0.5=.
26、(1)证明:∵BD⊥AD,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠CAE+∠BAD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴AE=BD,AD=CE,
∴DE=AD+AE=BD+CE;
(2)解:DE=BD+CE,
理由如下:在△ABD中,∠ABD=180°﹣∠ADB﹣∠BAD,
∵∠CAE=180°﹣∠BAC﹣∠BAD,∠BDA=∠BAC,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴AE=BD,AD=CE,
∴DE=AD+AE=BD+CE;
(3)解:如图③,作AE⊥x轴于E,BF⊥x轴于F,
由(1)可知,△AEC≌△CFB,
∴CF=AE=3,BF=CE=OE﹣OC=4,
∴OF=CF﹣OC=1,
∴点B的坐标为(1,4).
同课章节目录
