第4章4.3指数函数与对数函数的关系 同步练习(含答案)
文档属性
| 名称 | 第4章4.3指数函数与对数函数的关系 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 616.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-14 09:25:12 | ||
图片预览




文档简介
第4章4.3指数函数与对数函数的关系同步练习
2022——2023学年高中数学人教B版(2019)第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若函数的反函数为,则等于( )
A.2 B.-2 C.3 D.-1
2.函数的反函数的表达式为( )
A. B.
C. D.
3.函数与函数的图象( )
A.关于x轴对称 B.关于y轴对称 C.关于原点对称 D.关于直线对称
4.记函数的反函数为,则等于( )
A. B. C. D.
5.若函数在上存在反函数,则实数a的取值范围为( )
A. B. C. D.
6.已知函数的图象与函数的图象关于直线对称,则( )
A. B.
C. D.
7.函数的反函数的图象为( )
A. B.
C. D.
8.函数(,且)的反函数的图象过点,则a的值为( )
A.2 B. C.2或 D.3
9.函数的反函数的定义域为( )
A. B. C. D.
10.方程的根的情况是( )
A.仅有一个正根 B.有两个正根 C.有两个负根 D.有一个正根和一个负根
11.已知函数的图像过点,而且其反函数的图像过点,则是( )
A.增函数 B.减函数 C.奇函数 D.偶函数
12.专家对某地区新型流感爆发趋势进行研究发现,从确诊第一名患者开始累计时间(单位:天)与病情爆发系数之间,满足函数模型:,当时,标志着疫情将要局部爆发,则此时约为(参考数据:)( )
A. B. C. D.
13.方程的解集为( )
A. B. C. D.
14.设,,均为实数,且,,,则( )
A. B. C. D.
15.若,则函数与在第一象限内的图象关于( )对称.
A.直线 B.轴 C.轴 D.原点
二、填空题
16.若点在函数的图像上,点在的反函数图像上,则______.
17.函数的表达式为,设是其反函数,则______.
18.设是定义在上的奇函数,当时,,若存在反函数,则的取值范围是______________.
19.函数的图像与函数的图像关于直线______对称.
20.若函数的图象与函数的图象关于直线对称,则的表达式是______.
三、解答题
21.解关于的方程:
(1);
(2).
22.已知函数是函数的反函数,函数的图像和函数的图像关于直线成轴对称图形,记.
(1)求的解析式及定义域;
(2)在函数的图像上是否存在两个不同的点A、B,使直线AB恰好与y轴垂直?若存在,求出A、B的坐标;若不存在,请说明理由.
23.设同时满足条件和对任意,都有成立.
(1)求的解析式;
(2)设函数的定义域为,且在定义域内.若函数的图象与的图象关于直线对称,求.
24.已知函数.
(1)求函数的反函数,并求出反函数的定义域;
(2)判断并证明的单调性.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】先求出反函数,直接代入即可求解.
【详解】由得,
又,∴,∴(),∴.
故选:B
2.B
【分析】利用反函数的定义求解.
【详解】由得,
令得,
所以函数的反函数的表达式为,
故选:B
3.D
【分析】根据反函数的性质以及对数函数和指数函数互为反函数可求得的答案.
【详解】解:与互为反函数,所以它们的图象关于直线对称.
故选:D.
4.B
【分析】求出函数的解析式,可求得的值.
【详解】由可得,可得,则,
因此,.
故选:B.
5.B
【分析】若函数在上存在反函数,则函数在上单调即可,则是函数的单调区间的子集,从而可得答案.
【详解】解:若函数在上存在反函数,
则函数在上单调即可,
又因为函数在上递减,在上递增,
所以,所以.
故选:B.
6.D
【分析】分析得出函数的解析式,即可得出的表达式.
【详解】因为函数的图象与函数的图象关于直线对称,则,
因此,.
故选:D.
7.D
【分析】求出函数的反函数,即可得出结论.
【详解】由得,可得,
故函数的反函数的解析式为,
而函数的图象可由函数的图象向下平移个单位得到.
故选:D.
8.B
【分析】法一:求出反函数,将点代入反函数即可求解;法二:根据反函数的性质可得函数的图象过点,代入求解即可.
【详解】法一:函数(,且)的反函数为(,且),
故的图象过点,则.
法二:∵函数(,且)的反函数的图象过点,
∴函数(,且)的图象过点,
∴,即.
故选:B
9.A
【分析】根据反函数的定义,函数的值域即为其反函数的定义域,值域求出即可得解.
【详解】解:因为,所以,所以,
所以,
即其反函数的定义域为.
故选:A.
10.D
【分析】将方程的根的情况转化为函数,图像交点的问题,画出两函数的图像可得答案
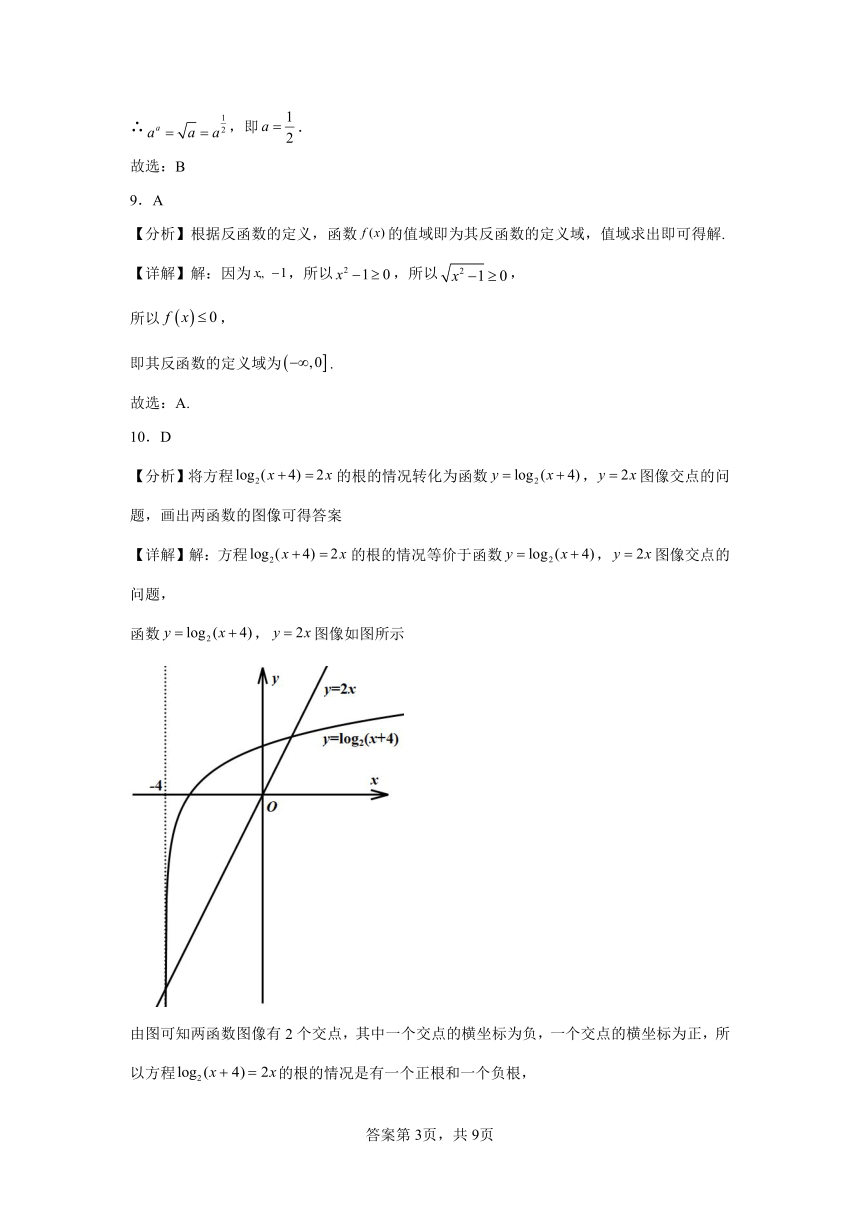
【详解】解:方程的根的情况等价于函数,图像交点的问题,
函数,图像如图所示
由图可知两函数图像有2个交点,其中一个交点的横坐标为负,一个交点的横坐标为正,所以方程的根的情况是有一个正根和一个负根,
故选:D
11.A
【分析】由反函数的意义,可知当反函数的图象过点时,原函数的图象过点,结合函数的图象过点,即可求解.
【详解】由反函数的意义,可知当反函数的图象过点时,原函数的图象过点,
结合函数的图象过点,
可得,
即函数为,
由对数型复合函数可知函数为增函数,且为非奇非偶函数.
故选:A.
12.A
【分析】根据列式,并根据给出参考数据,结合指数函数的性质解相应的指数方程,即可得答案.
【详解】解:因为,,
所以,即,
所以,由于,故,
所以,所以,解得.
故选:A.
13.D
【分析】根据指对数的关系解方程,即可求解集.
【详解】由得:,
故选:D.
14.A
【分析】利用指数函数与对数函数的图象与性质画出图象,即可得出结论.
【详解】解:如图所示,由图象可知:.
故选:A.
15.A
【解析】把条件根据对数函数的运算法则得到,得到与在大于0时互为反函数,得到关于对称即可.
【详解】解:由,得到即,则与在时互为反函数,所以关于对称.
故选:A.
【点睛】考查对数的运算,以及两个幂函数当大于0时指数互为倒数即互为反函数,则两个函数图象在第一象限关于对称,属于基础题.
16.
【分析】根据反函数性质,列方程,求解即可.
【详解】因为点在函数的图像上,所以,计算得,
因为,所以的反函数为,
又因为点在的反函数图像上,所以,
因为,所以,即得.
故答案为: .
17.
【分析】互换,即可求出原函数的反函数及定义域.
【详解】解:由题意,
在中,,
互换得,,
∴
故答案为:
18.或.
【分析】先求出的解析式,若存在反函数,则在每段单调且各段值域无重合,计算得解.
【详解】当时,,,是定义在上的奇函数,所以,即时,,所以,
若存在反函数,则在每段单调且各段值域无重合,
当,,;
所以或
所以或.
故答案为:或.
19.
【分析】利用反函数的性质即求.
【详解】因为与互为反函数,
所以函数的图像与函数的图像关于直线对称.
故答案为:.
20.
【分析】根据反函数的定义直接写出函数解析式.
【详解】由函数的图象与函数的图象关于直线对称,
可知函数与函数互为反函数,
故,
故答案为:.
21.(1);
(2).
【分析】(1)利用对数的运算法则及换底公式可得,即求;
(2)由题可得,令,则,可求,即求.
(1)
由题可得,
∴,即,
整理得,
解出或者(舍),
故该方程的根为;
(2)
该方程变形为,
令,则可得出,
解得,
∴.
22.(1),
(2)不存在,因为是单调递减函数
【分析】(1)利用求反函数的方法求出即得解;
(2)判断函数的单调性即得解.
(1)
解:由得,
因为函数是定义域上的减函数,所以,
所以,,
因为,所以
所以,,
所以,.
(2)
解:,.
所以函数是定义域上的减函数.
又是定义域上的减函数,
所以是定义域上的单调递减函数(减+减=减),
所以满足条件的点A、B不存在.
23.(1);(2).
【分析】(1)由求出的值,由可求得的值,进而可得的解析式;
(2),根据单调性求出的值域即为的定义域,设点是函数的图象上任意一点,点在函数的图象上,代入解析式,进而可得.
【详解】(1)由,得,
由,得,
即对任意恒成立,
因为,所以,可得:,
所以.
(2)由题意知,当时,,
因为在上单调递增,所以,
设点是函数的图象上任意一点,它关于直线对称的点为,依题意知点应该在函数的图象上,
即,所以,
即.
24.(1),定义域为;(2)在区间上单调递增,证明见解析.
【分析】(1)利用反函数的定义以及函数值域的求法即可求解.
(2)利用函数的单调性定义即可求解.
【详解】(1)解析:∵,开平方得,
整理得,
∴,定义域为.
(2)在区间上单调递增,证明如下:
任取,且,
则
,
因为,,,
所以,即
答案第1页,共2页
答案第1页,共2页
2022——2023学年高中数学人教B版(2019)第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若函数的反函数为,则等于( )
A.2 B.-2 C.3 D.-1
2.函数的反函数的表达式为( )
A. B.
C. D.
3.函数与函数的图象( )
A.关于x轴对称 B.关于y轴对称 C.关于原点对称 D.关于直线对称
4.记函数的反函数为,则等于( )
A. B. C. D.
5.若函数在上存在反函数,则实数a的取值范围为( )
A. B. C. D.
6.已知函数的图象与函数的图象关于直线对称,则( )
A. B.
C. D.
7.函数的反函数的图象为( )
A. B.
C. D.
8.函数(,且)的反函数的图象过点,则a的值为( )
A.2 B. C.2或 D.3
9.函数的反函数的定义域为( )
A. B. C. D.
10.方程的根的情况是( )
A.仅有一个正根 B.有两个正根 C.有两个负根 D.有一个正根和一个负根
11.已知函数的图像过点,而且其反函数的图像过点,则是( )
A.增函数 B.减函数 C.奇函数 D.偶函数
12.专家对某地区新型流感爆发趋势进行研究发现,从确诊第一名患者开始累计时间(单位:天)与病情爆发系数之间,满足函数模型:,当时,标志着疫情将要局部爆发,则此时约为(参考数据:)( )
A. B. C. D.
13.方程的解集为( )
A. B. C. D.
14.设,,均为实数,且,,,则( )
A. B. C. D.
15.若,则函数与在第一象限内的图象关于( )对称.
A.直线 B.轴 C.轴 D.原点
二、填空题
16.若点在函数的图像上,点在的反函数图像上,则______.
17.函数的表达式为,设是其反函数,则______.
18.设是定义在上的奇函数,当时,,若存在反函数,则的取值范围是______________.
19.函数的图像与函数的图像关于直线______对称.
20.若函数的图象与函数的图象关于直线对称,则的表达式是______.
三、解答题
21.解关于的方程:
(1);
(2).
22.已知函数是函数的反函数,函数的图像和函数的图像关于直线成轴对称图形,记.
(1)求的解析式及定义域;
(2)在函数的图像上是否存在两个不同的点A、B,使直线AB恰好与y轴垂直?若存在,求出A、B的坐标;若不存在,请说明理由.
23.设同时满足条件和对任意,都有成立.
(1)求的解析式;
(2)设函数的定义域为,且在定义域内.若函数的图象与的图象关于直线对称,求.
24.已知函数.
(1)求函数的反函数,并求出反函数的定义域;
(2)判断并证明的单调性.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】先求出反函数,直接代入即可求解.
【详解】由得,
又,∴,∴(),∴.
故选:B
2.B
【分析】利用反函数的定义求解.
【详解】由得,
令得,
所以函数的反函数的表达式为,
故选:B
3.D
【分析】根据反函数的性质以及对数函数和指数函数互为反函数可求得的答案.
【详解】解:与互为反函数,所以它们的图象关于直线对称.
故选:D.
4.B
【分析】求出函数的解析式,可求得的值.
【详解】由可得,可得,则,
因此,.
故选:B.
5.B
【分析】若函数在上存在反函数,则函数在上单调即可,则是函数的单调区间的子集,从而可得答案.
【详解】解:若函数在上存在反函数,
则函数在上单调即可,
又因为函数在上递减,在上递增,
所以,所以.
故选:B.
6.D
【分析】分析得出函数的解析式,即可得出的表达式.
【详解】因为函数的图象与函数的图象关于直线对称,则,
因此,.
故选:D.
7.D
【分析】求出函数的反函数,即可得出结论.
【详解】由得,可得,
故函数的反函数的解析式为,
而函数的图象可由函数的图象向下平移个单位得到.
故选:D.
8.B
【分析】法一:求出反函数,将点代入反函数即可求解;法二:根据反函数的性质可得函数的图象过点,代入求解即可.
【详解】法一:函数(,且)的反函数为(,且),
故的图象过点,则.
法二:∵函数(,且)的反函数的图象过点,
∴函数(,且)的图象过点,
∴,即.
故选:B
9.A
【分析】根据反函数的定义,函数的值域即为其反函数的定义域,值域求出即可得解.
【详解】解:因为,所以,所以,
所以,
即其反函数的定义域为.
故选:A.
10.D
【分析】将方程的根的情况转化为函数,图像交点的问题,画出两函数的图像可得答案
【详解】解:方程的根的情况等价于函数,图像交点的问题,
函数,图像如图所示
由图可知两函数图像有2个交点,其中一个交点的横坐标为负,一个交点的横坐标为正,所以方程的根的情况是有一个正根和一个负根,
故选:D
11.A
【分析】由反函数的意义,可知当反函数的图象过点时,原函数的图象过点,结合函数的图象过点,即可求解.
【详解】由反函数的意义,可知当反函数的图象过点时,原函数的图象过点,
结合函数的图象过点,
可得,
即函数为,
由对数型复合函数可知函数为增函数,且为非奇非偶函数.
故选:A.
12.A
【分析】根据列式,并根据给出参考数据,结合指数函数的性质解相应的指数方程,即可得答案.
【详解】解:因为,,
所以,即,
所以,由于,故,
所以,所以,解得.
故选:A.
13.D
【分析】根据指对数的关系解方程,即可求解集.
【详解】由得:,
故选:D.
14.A
【分析】利用指数函数与对数函数的图象与性质画出图象,即可得出结论.
【详解】解:如图所示,由图象可知:.
故选:A.
15.A
【解析】把条件根据对数函数的运算法则得到,得到与在大于0时互为反函数,得到关于对称即可.
【详解】解:由,得到即,则与在时互为反函数,所以关于对称.
故选:A.
【点睛】考查对数的运算,以及两个幂函数当大于0时指数互为倒数即互为反函数,则两个函数图象在第一象限关于对称,属于基础题.
16.
【分析】根据反函数性质,列方程,求解即可.
【详解】因为点在函数的图像上,所以,计算得,
因为,所以的反函数为,
又因为点在的反函数图像上,所以,
因为,所以,即得.
故答案为: .
17.
【分析】互换,即可求出原函数的反函数及定义域.
【详解】解:由题意,
在中,,
互换得,,
∴
故答案为:
18.或.
【分析】先求出的解析式,若存在反函数,则在每段单调且各段值域无重合,计算得解.
【详解】当时,,,是定义在上的奇函数,所以,即时,,所以,
若存在反函数,则在每段单调且各段值域无重合,
当,,;
所以或
所以或.
故答案为:或.
19.
【分析】利用反函数的性质即求.
【详解】因为与互为反函数,
所以函数的图像与函数的图像关于直线对称.
故答案为:.
20.
【分析】根据反函数的定义直接写出函数解析式.
【详解】由函数的图象与函数的图象关于直线对称,
可知函数与函数互为反函数,
故,
故答案为:.
21.(1);
(2).
【分析】(1)利用对数的运算法则及换底公式可得,即求;
(2)由题可得,令,则,可求,即求.
(1)
由题可得,
∴,即,
整理得,
解出或者(舍),
故该方程的根为;
(2)
该方程变形为,
令,则可得出,
解得,
∴.
22.(1),
(2)不存在,因为是单调递减函数
【分析】(1)利用求反函数的方法求出即得解;
(2)判断函数的单调性即得解.
(1)
解:由得,
因为函数是定义域上的减函数,所以,
所以,,
因为,所以
所以,,
所以,.
(2)
解:,.
所以函数是定义域上的减函数.
又是定义域上的减函数,
所以是定义域上的单调递减函数(减+减=减),
所以满足条件的点A、B不存在.
23.(1);(2).
【分析】(1)由求出的值,由可求得的值,进而可得的解析式;
(2),根据单调性求出的值域即为的定义域,设点是函数的图象上任意一点,点在函数的图象上,代入解析式,进而可得.
【详解】(1)由,得,
由,得,
即对任意恒成立,
因为,所以,可得:,
所以.
(2)由题意知,当时,,
因为在上单调递增,所以,
设点是函数的图象上任意一点,它关于直线对称的点为,依题意知点应该在函数的图象上,
即,所以,
即.
24.(1),定义域为;(2)在区间上单调递增,证明见解析.
【分析】(1)利用反函数的定义以及函数值域的求法即可求解.
(2)利用函数的单调性定义即可求解.
【详解】(1)解析:∵,开平方得,
整理得,
∴,定义域为.
(2)在区间上单调递增,证明如下:
任取,且,
则
,
因为,,,
所以,即
答案第1页,共2页
答案第1页,共2页
