第5章5.1统计 同步练习(含解析)
文档属性
| 名称 | 第5章5.1统计 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 908.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-14 09:25:41 | ||
图片预览




文档简介
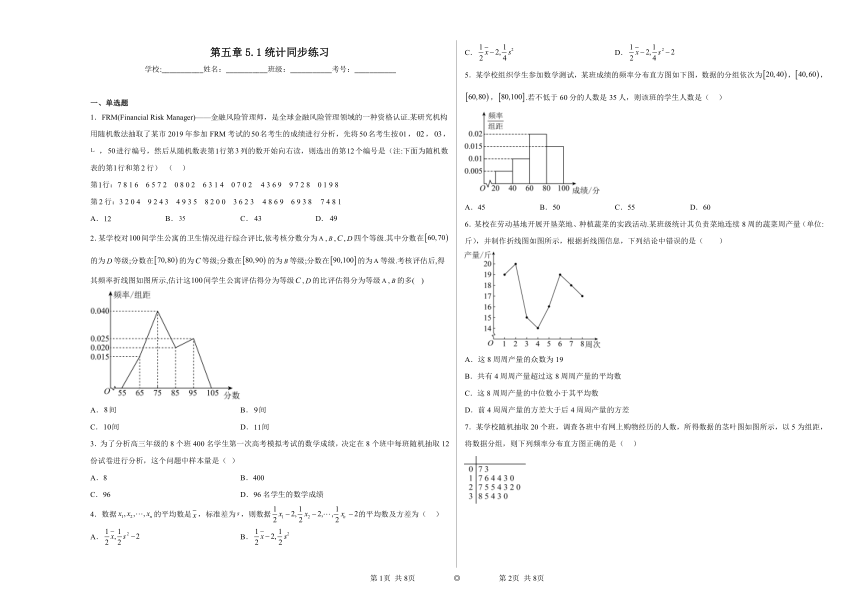
第五章5.1统计同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.FRM(Financial Risk Manager)——金融风险管理师,是全球金融风险管理领域的一种资格认证.某研究机构用随机数法抽取了某市2019年参加FRM考试的名考生的成绩进行分析,先将名考生按,,,,进行编号,然后从随机数表第行第列的数开始向右读,则选出的第个编号是(注:下面为随机数表的第行和第行) ( )
第行:7 8 1 6 6 5 7 2 0 8 0 2 6 3 1 4 0 7 0 2 4 3 6 9 9 7 2 8 0 1 9 8
第行:3 2 0 4 9 2 4 3 4 9 3 5 8 2 0 0 3 6 2 3 4 8 6 9 6 9 3 8 7 4 8 1
A. B. C. D.
2.某学校对间学生公寓的卫生情况进行综合评比,依考核分数分为,,,四个等级.其中分数在的为等级;分数在的为等级;分数在的为等级;分数在的为等级.考核评估后,得其频率折线图如图所示,估计这间学生公寓评估得分为等级,的比评估得分为等级,的多( )
A.间 B.间
C.间 D.间
3.为了分析高三年级的8个班400名学生第一次高考模拟考试的数学成绩,决定在8个班中每班随机抽取12份试卷进行分析,这个问题中样本量是( )
A.8 B.400
C.96 D.96名学生的数学成绩
4.数据的平均数是,标准差为,则数据的平均数及方差为( )
A. B.
C. D.
5.某学校组织学生参加数学测试,某班成绩的频率分布直方图如下图,数据的分组依次为,,,.若不低于60分的人数是35人,则该班的学生人数是( )
A.45 B.50 C.55 D.60
6.某校在劳动基地开展开垦菜地、种植蔬菜的实践活动.某班级统计其负责菜地连续8周的蔬菜周产量(单位:斤),并制作折线图如图所示,根据折线图信息,下列结论中错误的是( )
A.这8周周产量的众数为19
B.共有4周周产量超过这8周周产量的平均数
C.这8周周产量的中位数小于其平均数
D.前4周周产量的方差大于后4周周产量的方差
7.某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示,以5为组距,将数据分组,则下列频率分布直方图正确的是( )
A. B.
C. D.
8.比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图1所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力优于甲的逻辑推理能力
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
9.气象意义上从春季进入夏季的标志为“连续5天的日平均温度均不低于℃”.现有甲、乙、丙三地连续5天的日平均温度(单位:℃)的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体平均数为24;
③丙地:5个数据中有一个数据是32,总体平均数为26,总体方差为10.8.
则肯定进入夏季的地区有( )
A.0个 B.1个 C.2个 D.3个
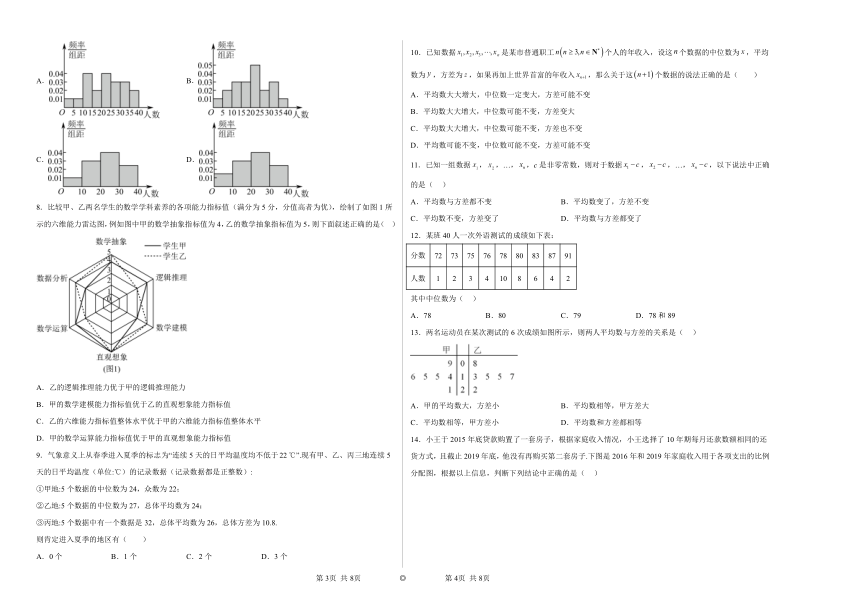
10.已知数据是某市普通职工个人的年收入,设这个数据的中位数为,平均数为,方差为,如果再加上世界首富的年收入,那么关于这个数据的说法正确的是( )
A.平均数大大增大,中位数一定变大,方差可能不变
B.平均数大大增大,中位数可能不变,方差变大
C.平均数大大增大,中位数可能不变,方差也不变
D.平均数可能不变,中位数可能不变,方差可能不变
11.已知一组数据,,…,,c是非零常数,则对于数据,,…,,以下说法中正确的是( )
A.平均数与方差都不变 B.平均数变了,方差不变
C.平均数不变,方差变了 D.平均数与方差都变了
12.某班40人一次外语测试的成绩如下表:
分数 72 73 75 76 78 80 83 87 91
人数 1 2 3 4 10 8 6 4 2
其中中位数为( )
A.78 B.80 C.79 D.78和89
13.两名运动员在某次测试的6次成绩如图所示,则两人平均数与方差的关系是( )
A.甲的平均数大,方差小 B.平均数相等,甲方差大
C.平均数相等,甲方差小 D.平均数和方差都相等
14.小王于2015年底贷款购置了一套房子,根据家庭收入情况,小王选择了10年期每月还款数额相同的还货方式,且截止2019年底,他没有再购买第二套房子.下图是2016年和2019年家庭收入用于各项支出的比例分配图,根据以上信息,判断下列结论中正确的是( )
A.小王一家2019年用于饮食支出费用与2016年相同
B.小王一家2019年用于其他方面的支出费用是2016年的3倍
C.小王一家2019年的家庭收入比2016年增加了一倍
D.小王一家2019年的房贷支出比2016年减少了
15.下列调查中样本合理的是( )
A.调查高一年级每个班数学成绩在前十名的学生,以了解哪名老师最受学生欢迎
B.从一万多名工人中,选出100名代表,由他们投票表决,了解工人对厂长的信任情况
C.到老年公寓进行调查,了解全市老年人的健康状况
D.医生为了了解病人的血液的各项指标是否正常,只是将病人指尖刺破,抽取少量的血液进行检验
二、填空题
16.某校规定:学生期末总评成绩由卷面成绩、研究性学习成绩、平日成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科三部分成绩分别是90分、80分、85分,则小明的期末数学总评成绩为________分.
17.2020年新冠肺炎疫情期间,为停课不停学,某高中实施网上教学.该高中为了解网课学习效果,组织了一次网上测试.并利用分层抽样的方法从高中3个年级的学生中随机抽取了150人的测试成绩,其中高一、高二年级各抽取了40人,50人,若高三年级有学生1200人,则该高中共有学生_________人.
18.若3,x,3,4,y,z,8的平均数是12,则x,y,z的平均数是______.
19.随着移动互联网的发展,与餐饮美食相关的手机软件App层出不穷.为调查某两家订餐软件的商家的服务情况,统计了它们订餐“送达时间”(时间:分钟),得到茎叶图如图所示,则______更稳定.(填写“甲App”或“乙App”)
20.一所初级中学为了估计全体学生的平均身高和方差,通过抽样的方法从初一年级随机抽取了30人,计算得这30人的平均身高为154cm,方差为30;从初二年级随机抽取了40人,计算得这40人的平均身高为167cm,方差为20;从初三年级随机抽取了30人,计算得这30人的平均身高为170cm,方差为10.依据以上数据,若用样本的方差估计全校学生身高的方差,则全校学生身高方差的估计值为_________.
三、解答题
21.据统计,年月日至月日,省内外几个主要旅游景点客流量如下表:
张家界
凤凰
昆明
北京
如果你是旅行社老板,在明年的国庆长假中,你将如何安排你旅行社的导游、车辆和食宿.
22.某校初一某班数学测试成绩如下:
100分6人,99分5人,98分6人,95分4人,88分5人,85分5人,80分8人,79分2人,78分4人,65分3人,50分2人
(1)如 85 分以上(含 85 分)为优秀,则成绩为优秀的人的频率是多少?
(2)利用计算加权平均数的方法,求出这次考试的平均成绩.
23.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是 0.30,0.40,0.15,0.10,0.05.求:高一参赛学生的成绩的众数、中位数.
24.如图是某高校土木工程系大四年级名学生期末考试专业成绩的频率折线图,其中组距为,且本次考试中最低分为分,最高分为分.根据图中所提供的信息,判断下列说法哪些正确,哪些不正确,并说明理由.
①成绩是分的有人;
②成绩是分的人数比成绩是分的人数多;
③成绩落在分的有人;
④成绩落在分的有人.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】理解题意,根据题意从随机数表第行第列的数开始向右读,逐个数,选出第个编号即可.
【详解】由随机数表的读法可得,所读的数(大于50的跳过,重复的不选取)依次为16,08,02,14,07,43,28,01,32,04,49,35,…,所以选出的第12个编号是35.
故选:B.
2.C
【分析】根据频率折线图分别求出分数为等级的频率,再根据总数作差即可.
【详解】由频率折线图可知,
分数为等级的频率为;
分数为等级的频率为;
分数为等级的频率为;
分数为等级的频率为,
所以,
即评估得分为等级,的比评估得分为等级,的多间.
故选:C.
3.C
【分析】直接根据总体,样本,样本量的定义得到答案.
【详解】400名学生第一次高考模拟考试的数学成绩是总体,
从8个班中每班抽取的12名学生的数学成绩是样本,400是总体个数,96是样本量.
故选:C
4.C
【分析】直接利用平均数、标准差和方差的公式求解.
【详解】因为的平均数是,标准差为,
所以,,
所以数据的平均数为:
,
数据的方差为:
.
故选:C.
5.B
【分析】根据频率分布直方图计算的频率,然后根据不低于60分的人数计算即可.
【详解】由题知:不低于60分的频率为:,
又不低于60分的人数是35人,所以该班的学生人数是.
故选:B
6.C
【分析】直接根据折线图求众数,判断A,计算平均数及中位数,判断B,C,根据方差的意义判断D.
【详解】由图知,这八周周产量的众数为19,A正确,
这8周周产量的平均数为,
所以共有周周产量超过周产量的平均数,B正确.
中位数为,所以中位数大于平均数,C错误.
根据折线图可知,前四周波动比后四周的波动要大,
所以前四周周产量的方差大于后四周周产量的方差, D正确.
故选:C.
7.A
【分析】解法一:根据题中数据分别计算各组的频数,频率及,观察各选项的频率分布直方图即可得解.
解法二:选项C,D中组距不符合要求,由茎叶图知落在区间与上的频数相等,故频率、也分别相等,比较选项A,B即可得解.
【详解】解法一:由题意知样本容量为20,组距为5,列表如下:
分组 频数 频率
1 0.01
1 0.01
4 0.04
2 0.02
4 0.04
3 0.03
3 0.03
2 0.02
合计 20 1
观察各选项的频率分布直方图知A正确.
解法二:选项C,D中组距不符合要求,由茎叶图知落在区间与上的频数相等,故频率、也分别相等,比较选项A,B知A正确.
故选:A.
8.C
【分析】利用雷达图对每一个选项的命题逐一分析推理得解.
【详解】A:甲的逻辑推理能力指标值为4,优于乙的逻辑推理能力指标值为3,故错误;
B:甲的数学建模能力指标值为3,乙的直观想象能力指标值为5,所以乙的直观想象能力指标值优于甲的数学建模能力指标值,故错误;
C:甲的六维能力指标值的平均值为,乙的六维能力指标值的平均值为,因为,故正确;
D:甲的数学运算能力指标值为4,甲的直观想象能力指标值为5,所以甲的数学运算能力指标值不优于甲的直观想象能力指标值,故错误.
故选:C
9.C
【分析】由已知可推得甲地连续5天的日平均温度最低的3个数依次为22、22、24,即可判断甲地;举例即可判断乙地、丙地.
【详解】甲地:5个数据的中位数为24,众数为22,则甲地连续5天的日平均温度最低的3个数依次为22、22、24,即其连续5天的日平均温度不低于22 ℃,所以甲地肯定进入夏季;
乙地:5个数据的中位数为27,总体平均数为24,当5个数据为19,20,27,27,27时,其连续5天的日平均温度有低于22 ℃的,不符合进入夏季的标准;
丙地:5个数据中有一个数据是32,总体平均数为26,若有低于22的,不妨取21,则方差超过了10.8,可以知道其连续5天的日平均温度不低于22 ℃,所以丙地肯定进入夏季.
综上所述,肯定进入夏季的地区有2个.
故选:C.
10.B
【分析】根据极端值对平均数、中位数和方差的影响直接判断即可.
【详解】插入的时大的极端值,则平均数增加,中位数可能不发生变化,方差因为数据更加分散而变大,ACD错误,B正确.
故选:B.
11.B
【分析】根据平均数与方差的定义直接计算,逐项检验即可得到答案.
【详解】设的平均数为,即,
则其方差为:,
所以的平均数为:,
的方差为:
,
所以平均数变了,方差不变.
故选:B.
12.C
【分析】根据中位数的概念即可求得.
【详解】解:由题意得:所有成绩从小到大排列,第二十位是78,第二十一位是80,则中位数为.
故选:C
13.C
【分析】根据茎叶图看出两组数据,先求出两组数据的平均数,再求出两组数据的方差,比较两组数据的平均数及方差的大小,从而可得结论.
【详解】由茎叶图可看出甲的平均数是,
乙的平均数是,两组数据的平均数相等.
甲的方差是,
乙的方差是,甲的方差小于乙的方差.
故选:C.
14.B
【分析】对于A,小王一家2019年用于饮食的支出费用比2016年多;对于B,设2016年收入为,则2019年收入为,由此能求出小王一家2019年用于其他方面的支出费用是2016年的3倍;对于C,设2016年收入为,则2019年收入为;对于D,小王一家2019年用于房贷的支出费用与2016年相同.
【详解】对于A,小王一家2019年用于饮食的支出比例与跟2016年相同,但是由于2019年比2016年家庭收入多,小王一家2019年用于饮食的支出费用比2016年多,故A错误;
对于B,设2016年收入为,相同的还款数额在2016年占各项支出的,在2019年占各项支出的,年收入为:,小王一家2019年用于其他方面的支出费用为,小王一家2016年用于其他方面的支出费用为,
小王一家2019年用于其他方面的支出费用是2016年的3倍,故B正确;
对于C,设2016年收入为,则2019年收入为:,故C错误;
对于D,小王一家2019年用于房贷的支出费用与2016年相同,故D错误.
故选:B.
15.B
【分析】关键看抽本的样本是否具有随机性,由此能判断调查的样本是否合理.
【详解】解:对于A,这个调查的样本不合理,“了解哪名老师最受学生欢迎”的调查对象是教师,选项却是学生,故A错误;
对于B,从一万多名工人中,经过选举,确定100名代表,然后投票表决,了解工人们对厂长的信任情况,这个调查的样本合理,故B正确;
对于C,到老年公寓进行调查,这里调查不全面,不能了解全市老年人的健康状况,调查的样本不合理,故C错误;
对于D,医生为了了解病人的血液的各项指标是否正常,只是将病人指尖刺破,抽取少量的血液进行检验,调查不全面,故样本不合理,故D错误.
故选:B.
16.87
【分析】根据各部分所占比例计算学生期末总评成绩即可.
【详解】小明的期末数学总评成绩为:(分).
故答案为:87.
17.
【分析】根据分层抽样的分法,列出关系式,即可求解.
【详解】由题意知,高三年级抽取的学生数为,
设该高中的学生总数为,则,解得,
即该高中的学生共有人.
故答案为:.
18.22
【分析】由平均数的概念即可求解.
【详解】解:由题意得:
,即
故答案为:22
19.乙App
【分析】根据茎叶图分析数据的集中程度,即可判断订餐软件服务时间的稳定性.
【详解】由茎叶图知:乙送餐时间比较集中在之间,而甲送餐时间在、、分布较均匀,故乙送餐时间比甲要稳定.
故答案为:乙App
20.64.4
【分析】利用方差及平均数公式可得, 进而即得.
【详解】初一学生的样本记为,,…,,方差记为,初二学生的样本记为,,…,,方差记为,初三学生的样本记为,,…,,方差记为.
设样本的平均数为,则,
设样本的方差为.
则
又,
故,
同理,,
因此,
.
故答案为:.
21.应按照的比例安排导游,车辆和食宿
【分析】由表中数据可知四个景点的日客流量变化不大,只要按日平均客流量的比例来安排导游,车辆和食宿即可.
【详解】张家界日平均客流量:;
凤凰日平均客流量:;
昆明日平均客流量:;
北京日平均客流量:;
日平均客流量之比:,
应按照的比例安排导游,车辆和食宿.
22.(1);
(2)86.66.
【分析】(1)根据频率的概念结合条件即得;
(2)根据加权平均数公式即得.
【详解】(1)由题可知成绩为优秀的人的频率是
;
(2)这次考试的平均成绩为
.
23.众数为65,中位数为65
【分析】频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,即可得出众数,利用中位数的两边频率相等,即可求得中位数.
【详解】用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,
得众数为,
因为,
所以中位数在之间,设中位数为,
则,解得,所以中位数为.
24.①错误;②错误;③正确;④错误;理由见解析
【分析】根据折线图提供的数据及概率的意义判断可判断①②③④.
【详解】解:①错误,成绩落在分的人数为,但不能说成绩是分的有人;
②错误,由频率折线图看不出成绩是分的人数比成绩是分的人数多,
只能看出成绩落在分的人数和成绩落在分的人数相等;
③正确,成绩落在分的人数为;
④错误,无法判断成绩落在分的人数.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.FRM(Financial Risk Manager)——金融风险管理师,是全球金融风险管理领域的一种资格认证.某研究机构用随机数法抽取了某市2019年参加FRM考试的名考生的成绩进行分析,先将名考生按,,,,进行编号,然后从随机数表第行第列的数开始向右读,则选出的第个编号是(注:下面为随机数表的第行和第行) ( )
第行:7 8 1 6 6 5 7 2 0 8 0 2 6 3 1 4 0 7 0 2 4 3 6 9 9 7 2 8 0 1 9 8
第行:3 2 0 4 9 2 4 3 4 9 3 5 8 2 0 0 3 6 2 3 4 8 6 9 6 9 3 8 7 4 8 1
A. B. C. D.
2.某学校对间学生公寓的卫生情况进行综合评比,依考核分数分为,,,四个等级.其中分数在的为等级;分数在的为等级;分数在的为等级;分数在的为等级.考核评估后,得其频率折线图如图所示,估计这间学生公寓评估得分为等级,的比评估得分为等级,的多( )
A.间 B.间
C.间 D.间
3.为了分析高三年级的8个班400名学生第一次高考模拟考试的数学成绩,决定在8个班中每班随机抽取12份试卷进行分析,这个问题中样本量是( )
A.8 B.400
C.96 D.96名学生的数学成绩
4.数据的平均数是,标准差为,则数据的平均数及方差为( )
A. B.
C. D.
5.某学校组织学生参加数学测试,某班成绩的频率分布直方图如下图,数据的分组依次为,,,.若不低于60分的人数是35人,则该班的学生人数是( )
A.45 B.50 C.55 D.60
6.某校在劳动基地开展开垦菜地、种植蔬菜的实践活动.某班级统计其负责菜地连续8周的蔬菜周产量(单位:斤),并制作折线图如图所示,根据折线图信息,下列结论中错误的是( )
A.这8周周产量的众数为19
B.共有4周周产量超过这8周周产量的平均数
C.这8周周产量的中位数小于其平均数
D.前4周周产量的方差大于后4周周产量的方差
7.某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示,以5为组距,将数据分组,则下列频率分布直方图正确的是( )
A. B.
C. D.
8.比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图1所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力优于甲的逻辑推理能力
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
9.气象意义上从春季进入夏季的标志为“连续5天的日平均温度均不低于℃”.现有甲、乙、丙三地连续5天的日平均温度(单位:℃)的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体平均数为24;
③丙地:5个数据中有一个数据是32,总体平均数为26,总体方差为10.8.
则肯定进入夏季的地区有( )
A.0个 B.1个 C.2个 D.3个
10.已知数据是某市普通职工个人的年收入,设这个数据的中位数为,平均数为,方差为,如果再加上世界首富的年收入,那么关于这个数据的说法正确的是( )
A.平均数大大增大,中位数一定变大,方差可能不变
B.平均数大大增大,中位数可能不变,方差变大
C.平均数大大增大,中位数可能不变,方差也不变
D.平均数可能不变,中位数可能不变,方差可能不变
11.已知一组数据,,…,,c是非零常数,则对于数据,,…,,以下说法中正确的是( )
A.平均数与方差都不变 B.平均数变了,方差不变
C.平均数不变,方差变了 D.平均数与方差都变了
12.某班40人一次外语测试的成绩如下表:
分数 72 73 75 76 78 80 83 87 91
人数 1 2 3 4 10 8 6 4 2
其中中位数为( )
A.78 B.80 C.79 D.78和89
13.两名运动员在某次测试的6次成绩如图所示,则两人平均数与方差的关系是( )
A.甲的平均数大,方差小 B.平均数相等,甲方差大
C.平均数相等,甲方差小 D.平均数和方差都相等
14.小王于2015年底贷款购置了一套房子,根据家庭收入情况,小王选择了10年期每月还款数额相同的还货方式,且截止2019年底,他没有再购买第二套房子.下图是2016年和2019年家庭收入用于各项支出的比例分配图,根据以上信息,判断下列结论中正确的是( )
A.小王一家2019年用于饮食支出费用与2016年相同
B.小王一家2019年用于其他方面的支出费用是2016年的3倍
C.小王一家2019年的家庭收入比2016年增加了一倍
D.小王一家2019年的房贷支出比2016年减少了
15.下列调查中样本合理的是( )
A.调查高一年级每个班数学成绩在前十名的学生,以了解哪名老师最受学生欢迎
B.从一万多名工人中,选出100名代表,由他们投票表决,了解工人对厂长的信任情况
C.到老年公寓进行调查,了解全市老年人的健康状况
D.医生为了了解病人的血液的各项指标是否正常,只是将病人指尖刺破,抽取少量的血液进行检验
二、填空题
16.某校规定:学生期末总评成绩由卷面成绩、研究性学习成绩、平日成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科三部分成绩分别是90分、80分、85分,则小明的期末数学总评成绩为________分.
17.2020年新冠肺炎疫情期间,为停课不停学,某高中实施网上教学.该高中为了解网课学习效果,组织了一次网上测试.并利用分层抽样的方法从高中3个年级的学生中随机抽取了150人的测试成绩,其中高一、高二年级各抽取了40人,50人,若高三年级有学生1200人,则该高中共有学生_________人.
18.若3,x,3,4,y,z,8的平均数是12,则x,y,z的平均数是______.
19.随着移动互联网的发展,与餐饮美食相关的手机软件App层出不穷.为调查某两家订餐软件的商家的服务情况,统计了它们订餐“送达时间”(时间:分钟),得到茎叶图如图所示,则______更稳定.(填写“甲App”或“乙App”)
20.一所初级中学为了估计全体学生的平均身高和方差,通过抽样的方法从初一年级随机抽取了30人,计算得这30人的平均身高为154cm,方差为30;从初二年级随机抽取了40人,计算得这40人的平均身高为167cm,方差为20;从初三年级随机抽取了30人,计算得这30人的平均身高为170cm,方差为10.依据以上数据,若用样本的方差估计全校学生身高的方差,则全校学生身高方差的估计值为_________.
三、解答题
21.据统计,年月日至月日,省内外几个主要旅游景点客流量如下表:
张家界
凤凰
昆明
北京
如果你是旅行社老板,在明年的国庆长假中,你将如何安排你旅行社的导游、车辆和食宿.
22.某校初一某班数学测试成绩如下:
100分6人,99分5人,98分6人,95分4人,88分5人,85分5人,80分8人,79分2人,78分4人,65分3人,50分2人
(1)如 85 分以上(含 85 分)为优秀,则成绩为优秀的人的频率是多少?
(2)利用计算加权平均数的方法,求出这次考试的平均成绩.
23.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是 0.30,0.40,0.15,0.10,0.05.求:高一参赛学生的成绩的众数、中位数.
24.如图是某高校土木工程系大四年级名学生期末考试专业成绩的频率折线图,其中组距为,且本次考试中最低分为分,最高分为分.根据图中所提供的信息,判断下列说法哪些正确,哪些不正确,并说明理由.
①成绩是分的有人;
②成绩是分的人数比成绩是分的人数多;
③成绩落在分的有人;
④成绩落在分的有人.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】理解题意,根据题意从随机数表第行第列的数开始向右读,逐个数,选出第个编号即可.
【详解】由随机数表的读法可得,所读的数(大于50的跳过,重复的不选取)依次为16,08,02,14,07,43,28,01,32,04,49,35,…,所以选出的第12个编号是35.
故选:B.
2.C
【分析】根据频率折线图分别求出分数为等级的频率,再根据总数作差即可.
【详解】由频率折线图可知,
分数为等级的频率为;
分数为等级的频率为;
分数为等级的频率为;
分数为等级的频率为,
所以,
即评估得分为等级,的比评估得分为等级,的多间.
故选:C.
3.C
【分析】直接根据总体,样本,样本量的定义得到答案.
【详解】400名学生第一次高考模拟考试的数学成绩是总体,
从8个班中每班抽取的12名学生的数学成绩是样本,400是总体个数,96是样本量.
故选:C
4.C
【分析】直接利用平均数、标准差和方差的公式求解.
【详解】因为的平均数是,标准差为,
所以,,
所以数据的平均数为:
,
数据的方差为:
.
故选:C.
5.B
【分析】根据频率分布直方图计算的频率,然后根据不低于60分的人数计算即可.
【详解】由题知:不低于60分的频率为:,
又不低于60分的人数是35人,所以该班的学生人数是.
故选:B
6.C
【分析】直接根据折线图求众数,判断A,计算平均数及中位数,判断B,C,根据方差的意义判断D.
【详解】由图知,这八周周产量的众数为19,A正确,
这8周周产量的平均数为,
所以共有周周产量超过周产量的平均数,B正确.
中位数为,所以中位数大于平均数,C错误.
根据折线图可知,前四周波动比后四周的波动要大,
所以前四周周产量的方差大于后四周周产量的方差, D正确.
故选:C.
7.A
【分析】解法一:根据题中数据分别计算各组的频数,频率及,观察各选项的频率分布直方图即可得解.
解法二:选项C,D中组距不符合要求,由茎叶图知落在区间与上的频数相等,故频率、也分别相等,比较选项A,B即可得解.
【详解】解法一:由题意知样本容量为20,组距为5,列表如下:
分组 频数 频率
1 0.01
1 0.01
4 0.04
2 0.02
4 0.04
3 0.03
3 0.03
2 0.02
合计 20 1
观察各选项的频率分布直方图知A正确.
解法二:选项C,D中组距不符合要求,由茎叶图知落在区间与上的频数相等,故频率、也分别相等,比较选项A,B知A正确.
故选:A.
8.C
【分析】利用雷达图对每一个选项的命题逐一分析推理得解.
【详解】A:甲的逻辑推理能力指标值为4,优于乙的逻辑推理能力指标值为3,故错误;
B:甲的数学建模能力指标值为3,乙的直观想象能力指标值为5,所以乙的直观想象能力指标值优于甲的数学建模能力指标值,故错误;
C:甲的六维能力指标值的平均值为,乙的六维能力指标值的平均值为,因为,故正确;
D:甲的数学运算能力指标值为4,甲的直观想象能力指标值为5,所以甲的数学运算能力指标值不优于甲的直观想象能力指标值,故错误.
故选:C
9.C
【分析】由已知可推得甲地连续5天的日平均温度最低的3个数依次为22、22、24,即可判断甲地;举例即可判断乙地、丙地.
【详解】甲地:5个数据的中位数为24,众数为22,则甲地连续5天的日平均温度最低的3个数依次为22、22、24,即其连续5天的日平均温度不低于22 ℃,所以甲地肯定进入夏季;
乙地:5个数据的中位数为27,总体平均数为24,当5个数据为19,20,27,27,27时,其连续5天的日平均温度有低于22 ℃的,不符合进入夏季的标准;
丙地:5个数据中有一个数据是32,总体平均数为26,若有低于22的,不妨取21,则方差超过了10.8,可以知道其连续5天的日平均温度不低于22 ℃,所以丙地肯定进入夏季.
综上所述,肯定进入夏季的地区有2个.
故选:C.
10.B
【分析】根据极端值对平均数、中位数和方差的影响直接判断即可.
【详解】插入的时大的极端值,则平均数增加,中位数可能不发生变化,方差因为数据更加分散而变大,ACD错误,B正确.
故选:B.
11.B
【分析】根据平均数与方差的定义直接计算,逐项检验即可得到答案.
【详解】设的平均数为,即,
则其方差为:,
所以的平均数为:,
的方差为:
,
所以平均数变了,方差不变.
故选:B.
12.C
【分析】根据中位数的概念即可求得.
【详解】解:由题意得:所有成绩从小到大排列,第二十位是78,第二十一位是80,则中位数为.
故选:C
13.C
【分析】根据茎叶图看出两组数据,先求出两组数据的平均数,再求出两组数据的方差,比较两组数据的平均数及方差的大小,从而可得结论.
【详解】由茎叶图可看出甲的平均数是,
乙的平均数是,两组数据的平均数相等.
甲的方差是,
乙的方差是,甲的方差小于乙的方差.
故选:C.
14.B
【分析】对于A,小王一家2019年用于饮食的支出费用比2016年多;对于B,设2016年收入为,则2019年收入为,由此能求出小王一家2019年用于其他方面的支出费用是2016年的3倍;对于C,设2016年收入为,则2019年收入为;对于D,小王一家2019年用于房贷的支出费用与2016年相同.
【详解】对于A,小王一家2019年用于饮食的支出比例与跟2016年相同,但是由于2019年比2016年家庭收入多,小王一家2019年用于饮食的支出费用比2016年多,故A错误;
对于B,设2016年收入为,相同的还款数额在2016年占各项支出的,在2019年占各项支出的,年收入为:,小王一家2019年用于其他方面的支出费用为,小王一家2016年用于其他方面的支出费用为,
小王一家2019年用于其他方面的支出费用是2016年的3倍,故B正确;
对于C,设2016年收入为,则2019年收入为:,故C错误;
对于D,小王一家2019年用于房贷的支出费用与2016年相同,故D错误.
故选:B.
15.B
【分析】关键看抽本的样本是否具有随机性,由此能判断调查的样本是否合理.
【详解】解:对于A,这个调查的样本不合理,“了解哪名老师最受学生欢迎”的调查对象是教师,选项却是学生,故A错误;
对于B,从一万多名工人中,经过选举,确定100名代表,然后投票表决,了解工人们对厂长的信任情况,这个调查的样本合理,故B正确;
对于C,到老年公寓进行调查,这里调查不全面,不能了解全市老年人的健康状况,调查的样本不合理,故C错误;
对于D,医生为了了解病人的血液的各项指标是否正常,只是将病人指尖刺破,抽取少量的血液进行检验,调查不全面,故样本不合理,故D错误.
故选:B.
16.87
【分析】根据各部分所占比例计算学生期末总评成绩即可.
【详解】小明的期末数学总评成绩为:(分).
故答案为:87.
17.
【分析】根据分层抽样的分法,列出关系式,即可求解.
【详解】由题意知,高三年级抽取的学生数为,
设该高中的学生总数为,则,解得,
即该高中的学生共有人.
故答案为:.
18.22
【分析】由平均数的概念即可求解.
【详解】解:由题意得:
,即
故答案为:22
19.乙App
【分析】根据茎叶图分析数据的集中程度,即可判断订餐软件服务时间的稳定性.
【详解】由茎叶图知:乙送餐时间比较集中在之间,而甲送餐时间在、、分布较均匀,故乙送餐时间比甲要稳定.
故答案为:乙App
20.64.4
【分析】利用方差及平均数公式可得, 进而即得.
【详解】初一学生的样本记为,,…,,方差记为,初二学生的样本记为,,…,,方差记为,初三学生的样本记为,,…,,方差记为.
设样本的平均数为,则,
设样本的方差为.
则
又,
故,
同理,,
因此,
.
故答案为:.
21.应按照的比例安排导游,车辆和食宿
【分析】由表中数据可知四个景点的日客流量变化不大,只要按日平均客流量的比例来安排导游,车辆和食宿即可.
【详解】张家界日平均客流量:;
凤凰日平均客流量:;
昆明日平均客流量:;
北京日平均客流量:;
日平均客流量之比:,
应按照的比例安排导游,车辆和食宿.
22.(1);
(2)86.66.
【分析】(1)根据频率的概念结合条件即得;
(2)根据加权平均数公式即得.
【详解】(1)由题可知成绩为优秀的人的频率是
;
(2)这次考试的平均成绩为
.
23.众数为65,中位数为65
【分析】频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,即可得出众数,利用中位数的两边频率相等,即可求得中位数.
【详解】用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,
得众数为,
因为,
所以中位数在之间,设中位数为,
则,解得,所以中位数为.
24.①错误;②错误;③正确;④错误;理由见解析
【分析】根据折线图提供的数据及概率的意义判断可判断①②③④.
【详解】解:①错误,成绩落在分的人数为,但不能说成绩是分的有人;
②错误,由频率折线图看不出成绩是分的人数比成绩是分的人数多,
只能看出成绩落在分的人数和成绩落在分的人数相等;
③正确,成绩落在分的人数为;
④错误,无法判断成绩落在分的人数.
答案第1页,共2页
答案第1页,共2页
