第5章统计与概率 单元练习(含解析)
文档属性
| 名称 | 第5章统计与概率 单元练习(含解析) | 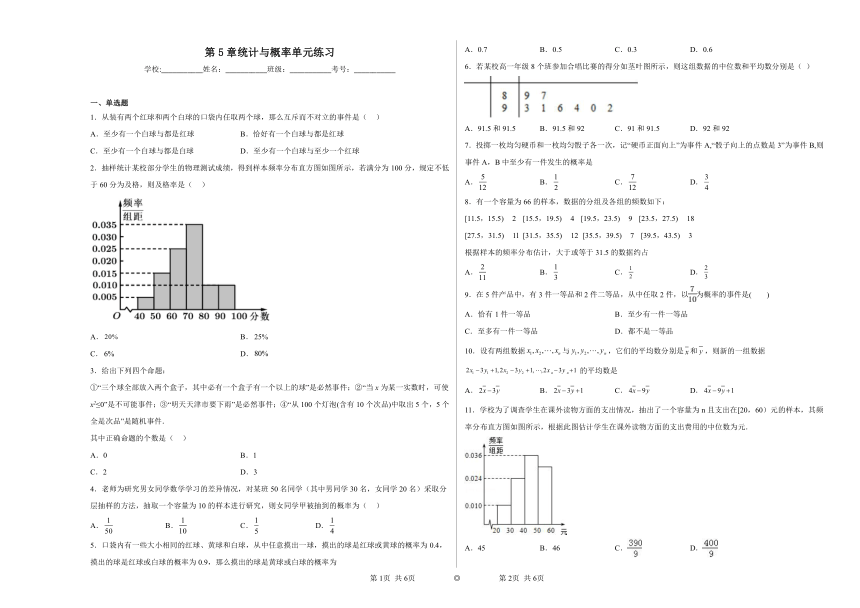 | |
| 格式 | docx | ||
| 文件大小 | 596.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-14 09:31:05 | ||
图片预览




文档简介
第5章统计与概率单元练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.从装有两个红球和两个白球的口袋内任取两个球,那么互斥而不对立的事件是( )
A.至少有一个白球与都是红球 B.恰好有一个白球与都是红球
C.至少有一个白球与都是白球 D.至少有一个白球与至少一个红球
2.抽样统计某校部分学生的物理测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A. B.
C. D.
3.给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②“当x为某一实数时,可使x2≤0”是不可能事件;③“明天天津市要下雨”是必然事件;④“从100个灯泡(含有10个次品)中取出5个,5个全是次品”是随机事件.
其中正确命题的个数是( )
A.0 B.1
C.2 D.3
4.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个容量为10的样本进行研究,则女同学甲被抽到的概率为( )
A. B. C. D.
5.口袋内有一些大小相同的红球、黄球和白球,从中任意摸出一球,摸出的球是红球或黄球的概率为0.4,摸出的球是红球或白球的概率为0.9,那么摸出的球是黄球或白球的概率为
A.0.7 B.0.5 C.0.3 D.0.6
6.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
A.91.5和91.5 B.91.5和92 C.91和91.5 D.92和92
7.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
A. B. C. D.
8.有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5,39.5) 7 [39.5,43.5) 3
根据样本的频率分布估计,大于或等于31.5的数据约占
A. B. C. D.
9.在5件产品中,有3件一等品和2件二等品,从中任取2件,以为概率的事件是( )
A.恰有1件一等品 B.至少有一件一等品
C.至多有一件一等品 D.都不是一等品
10.设有两组数据与,它们的平均数分别是和,则新的一组数据的平均数是
A. B. C. D.
11.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为元.
A.45 B.46 C. D.
12.甲、乙两位同学各拿出六张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是
A.甲得9张,乙得3张
B.甲得6张,乙得6张
C.甲得8张,乙得4张
D.甲得10张,乙得2张
13.某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各1人,则该小组数学成绩的平均数、众数、中位数分别为
A.85,85,85 B.87,85,86
C.87,85,85 D.87,85,90
14.从分别写有的张卡片中,任取张,这张上的字母恰好按字母顺序相邻的概率为( )
A. B. C. D.
15.某篮球运动员在最近几次参加的比赛中的得分情况如下表(没有罚球):
投篮次数 投中两分球的次数 投中三分球的次数
100 55 18
记该运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中不正确的是( )
A.P(A)=0.55 B.P(B)=0.18 C.P(C)=0.27 D.P(B+C)=0.55
二、填空题
16.某中学青年教师、中年教师和老年教师的人数比例为4∶5∶1,其中青年教师有120人.现采用分层抽样的方法从这所学校抽取容量为30的教师样本以了解教师的工作压力情况,则每位老年教师被抽到的概率为________.
17.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
学生 1号 2号 3号 4号 5号
甲班 6 7 7 8 7
乙班 6 7 6 7 9
则以上两组数据的方差中较小的一个为=____.
18.从字母中任取两个不同的字母,则取到字母的概率为_____________.
19.某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差___________________.
20.袋中装有大小相同的总数为个的黑球、白球若从袋中任意摸出个球,至少得到个白球的概率是,则从中任意摸出个球,得到的都是白球的概率为______.
三、解答题
21.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组,第二组,,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率;
(2)估计该校的800名男生的身高的平均数和中位数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x,y,事件,求.
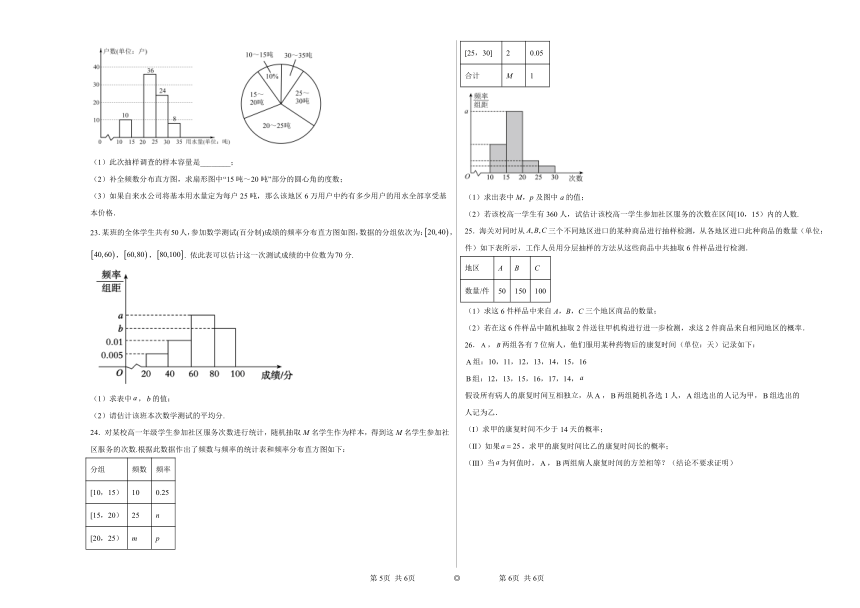
22.某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
用户用水量频数直方图 用户用水量扇形统计图
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格.
23.某班的全体学生共有人,参加数学测试(百分制)成绩的频率分布直方图如图,数据的分组依次为:,,,. 依此表可以估计这一次测试成绩的中位数为分.
(1)求表中,的值;
(2)请估计该班本次数学测试的平均分.
24.对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 频数 频率
[10,15) 10 0.25
[15,20) 25 n
[20,25) m p
[25,30] 2 0.05
合计 M 1
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[10,15)内的人数.
25.海关对同时从三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
地区 A B C
数量/件 50 150 100
(1)求这6件样品中来自A,B,C三个地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
26.,两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
组:10,11,12,13,14,15,16
组:12,13,15,16,17,14,
假设所有病人的康复时间互相独立,从,两组随机各选1人,组选出的人记为甲,组选出的
人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ)当为何值时,,两组病人康复时间的方差相等?(结论不要求证明)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】列举每个事件所包含的基本事件,结合互斥事件和对立事件的定义,依次验证即可.
【详解】解:对于A,事件:“至少有一个白球”与事件:“都是红球”不能同时发生,但是对立,故A错误;
对于B,事件:“恰好有一个白球”与事件:“都是红球”不能同时发生,但从口袋内任取两个球时还有可能是两个都是白球,
所以两个事件互斥而不对立,故B正确;
对于C,事件:“至少有一个白球”与事件:“都是白球”可以同时发生,所以这两个事件不是互斥的,故C错误;
对于D,事件:“至少有一个白球”与事件:“至少一个红球”可以同时发生,即“一个白球,一个红球” ,所以这两个事件不是互斥的,故D错误.
故选:B.
2.D
【分析】根据频率分布直方图,求出不低于60分的频率即可得出答案
【详解】解:根据频率分布直方图,
不低于60分的频率为,
所以及格率是.
故选:D.
3.C
【解析】利用必然事件的概念可以判断①是正确的命题,③是偶然事件,利用不可能事件的概念判断②正确,利用随机事件的概念判断④正确.
【详解】对于①,三个球全部放入两个盒子,有两种情况:1+2和3+0,故必有一个盒子有一个以上的球,所以该事件是必然事件,①正确;
对于②,x=0时x2=0,所以该事件不是不可能事件,②错误;
对于③,“明天天津市要下雨”是偶然事件,所以该事件是随机事件,③错误;
对于④,“从100个灯泡(含有10个次品)中取出5个,5个全是次品”,发生与否是随机的,所以该事件是随机事件,④正确.故正确命题有2个.
故选:C.
4.C
【分析】根据古典概型特点判断,每个个体被抽到的概率都是等可能的,结合古典概型公式即可求解
【详解】由题知,从50个人抽10个,每个个体被抽取的概率都是等可能的,为,则女同学甲被抽到的概率也为
故选:C
【点睛】本题考查随机事件的概率,属于基础题
5.A
【分析】设摸出红球的概率为,摸出黄球的概率是,摸出白球的概率为,求出、的值,相加即可求解.
【详解】设摸出红球的概率为,摸出黄球的概率是,摸出白球的概率为,
所以,且,
所以,,
所以
【点睛】本题主要考查了互斥事件的概率加法公式的应用,其中解答中熟记互斥事件的概率加法公式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.
6.A
【详解】8个班参加合唱比赛的得分从小到大排列分别是87,89,90,91,92,93,94,96,中位数是91,92,的平均数91.5,平均数是=91.5
7.C
【详解】试题分析:由题意可知,事件A与事件B是相互独立的,而事件A、B中至少有一件发生的事件包含、、,又,,所以所事件的概率为,故选C.
考点:相互独立事件概率的计算.
8.B
【详解】由题意,该样本中大于或等于31.5的数据的频率为,
所以可估计大于或等于31.5的数据约占.
故选:B.
9.C
【分析】将件一等品编号为,件二等品的编号为,列举出从中任取件的所有基本事件的总数,分别计算选项的概率,即可得到答案.
【详解】将3件一等品编号为1,2,3,2件二等品编号为4,5,从中任取2件有10种取法:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).其中恰含有1件一等品的取法有:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),恰有1件一等品的概率为P1=,恰有2件一等品的取法有:(1,2),(1,3),(2,3).故恰有2件一等品的概率为P2=,其对立事件是“至多有一件一等品”,概率为P3=1-P2=1-=.
【点睛】本题主要考查了古典概型及其概率的计算问题,其中明确古典概型的基本概念,以及古典的概型及概率的计算公式,合理作出计算是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
10.B
【分析】由题意结合平均数的性质即可求得结果.
【详解】由题意结合平均数的性质可知:
的平均数为,
的平均数为,
则的平均数为:.
故选:B.
11.D
【详解】试题分析:根据中位数是把频率分布直方图分成面积相等的两部分的平行于y轴的直线横坐标,求出即可.
解:第一个矩形的面积是0.10,第二个矩形的面积是0.24,
第三个矩形的面积是0.36,第四个矩形的面积是1﹣0.70=0.30;
前面两个矩形的面积和是0.34,故将第三个矩形分成4:5即可,
∴中位数是40+×10=.
故选D.
考点:频率分布直方图.
12.A
【详解】试题分析:由题意可知:乙获得12张游戏牌概率为,所以甲应分得张牌,乙应分得张牌,故选A.
考点:排列组合问题.
13.C
【详解】由题意可知,学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各有1人,则该小组数学成绩的平均数,成绩排列为75,80,85,85,85,85,90,90,95,100,可得众数为85,中位数,因此选C
14.B
【分析】分别求出从张卡片中任取张的取法总数和字母相邻的种数,根据古典概型概率公式求得结果.
【详解】从张卡片中任取张,共有:种取法
其中字母相邻的有:,,,,共种情况
所求概率
本题正确选项:
【点睛】本题考查古典概型概率问题的求解,属于基础题.
15.D
【分析】结合概率的计算公式求得正确答案.
【详解】依题意,,
,
所以D选项结论不正确.
故选:D
16.
【解析】先利用人数比例和青年教师人数计算该校全部教师人数,再利用古典概型计算每位老年教师被抽到的概率即可.
【详解】由青年教师、中年教师和老年教师的人数比例为4∶5∶1, 知青年教师的人数比例为,故该校全部教师人数为:120÷=300(人).
采用分层抽样的方法从这所学校抽取容量为30的教师样本,则每位老年教师被抽到的概率为P==.
故答案为:.
17.
【详解】试题分析:甲班的方差较小,数据的平均值为7,
故方差s2==.
考点:本题主要考查平均数及方差的概念和计算.
点评:简单题,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
18./0.4
【分析】利用古典概型中的列举法,即可求得所求.
【详解】从字母中任取两个不同的字母的基本事件有、、、、、、、、、,共个,
其中 “取到字母”(记为事件)所包含的基本事件有、、、,共个,
故所求事件的概率为.
故答案为:0.4
19.
【详解】试题分析:由平均数及方差的定义可得;
.
考点:样本数据的数字特征:平均值与方差.
20.
【详解】因为袋中装有大小相同的总数为5个的黑球、白球,若从袋中任意摸出2个球,共有10种,没有得到白球的概率为,设白球个数为x,黑球个数为5-x,那么可知白球共有3个,黑球有2个,因此可知填写为
21.(1);(2)平均数为,中位数为;(3).
【分析】(1)由频率分布直方图的性质求第七组的频率;
(2)根据平均数和中位数的定义利用频率分布直方图求平均数和中位数;
(3)确定样本空间,利用古典概型概率公式求概率.
【详解】解:(1)第六组的频率为,
∴第七组的频率为.
(2)由直方图得,身高在第一组的频率为,
身高在第二组的频率为,
身高在第三组的频率为,
身高在第四组的频率为,
由于,,
设这所学校的800名男生的身高中位数为m,则,
由得,
所以这所学校的800名男生的身高的中位数为174.5cm,平均数为
.
(3)第六组的抽取人数为4,设所抽取的人为a,b,c,d,
第八组的抽取人数为,设所抽取的人为A,B,
则从中随机抽取两名男生有ab,ac,ad,bc,bd,cd,aA,aB,bA,bB,cA,cB,dA,dB,AB共15种情况,
因事件发生当且仅当随机抽取的两名男生在同一组,所以事件E包含的基本事件为ab,ac,ad,bc,bd,cd,AB共7种情况.所以.
22.(1)答案见解析;(2)答案见解析,79.2°;(3)4.08万户.
【解析】(1)根据用户用水量在吨的户数以及所占比例得出样本容量;
(2)由样本容量减去用水15~20吨之外的户数,即可得出用水15~20吨的户数,再由用水15~20吨的户数占样本容量的比例求出圆心角;
(3)将样本中享受基本价格的户数所占样本的比例乘以得出答案.
【详解】(1);
(2)用水15~20吨的户数为100-10-36-24-8=22(户),
“15~20吨”部分的圆心角的度数为
(3)(万户)
所以该地区6万用户中约有4.08万户的用水全部享受基本价格.
23.(1),;(2)分.
【解析】(1)利用中位数为解得,然后利用频率和为求解;
(2)利用每个区间的中点值乘以该组的频率求和即可得到答案.
【详解】(1)由中位数为70可得,
,
解得.
又,
解得.
(2)由频率分布直方图可知,每组的频率依次为:,,,,则该班本次数学测试的平均分的估计值为:分.
【点睛】利用频率分布直方图估计样本的中位数及平均值的方法如下:
(1)平均数的估计值等于各小矩形面积乘以底边中点的横坐标之和;
(2)中位数的估计值等于把频率分布直方图分成面积相等的两部分时,分界线与横轴交点的横坐标.
24.(1)M=40,,;(2)90人.
【解析】(1)根据频数与频率的统计表和频率分布直方图计算可得结果;
(2)根据频数样本容量频率可求得结果.
【详解】(1)由[10,15)内的频数是10,频率是0.25知,,所以M=40.
因为频数之和为40,所以10+25+m+2=40,m=3..
因为a是对应分组[15,20)的频率与组距的商,所以.
(2)因为该校高一学生有360人,分组[10,15)内的频率是0.25,所以估计该校高一学生参加社区服务的次数在此区间内的人数为90人.
【点睛】关键点点睛:根据频数与频率的统计表和频率分布直方图计算求解是解题关键.
25.(1)1,3,2;(2).
【解析】(1)由分层抽样的性质运算即可得解;
(2)利用列举法,结合古典概型概率的计算公式,即可得解.
【详解】(1)由题意,样品中来自A地区商品的数量为,
来自B地区商品的数量为,
来自C地区商品的数量为;
(2)设来自地区的样品编号为,来自地区的样品编号为,,,
来自地区的样品编号为,,
则从6件样品中抽取2件产品的所有基本事件为:
,,,,,,,,
,,,,,,,共15个;
抽取的这2件产品来自相同地区的基本事件有:
,,,,共4个;
故所求概率.
【点睛】本题考查了分层抽样的应用及古典概型概率的求解,考查了运算求解能力,属于中档题.
26.(Ⅰ),(Ⅱ),(Ⅲ)或
【详解】试题分析:针对甲有7种情况,康复时间不少于14天有3种情况,概率为;如果,甲、乙随机各取一人有49种情况,用列举法列出甲的康复时间比乙的康复时间长的情况有10种,概率为,由于A组数据为10,11,12,13,14,15,16;B组数据调整为,12,13,14,15,16,17,或12,13,14,15,16,17,,由于,两组病人康复时间的方差相等,即波动相同,所以或.
试题解析:(Ⅰ)甲有7种取法,康复时间不少于14天的有3种取法,所以概率;
(Ⅱ) 如果,从,两组随机各选1人,组选出的人记为甲,组选出的人记为乙共有49种取法,甲的康复时间比乙的康复时间长的列举如下:(13,12),(14,12),(14,13),(15,12),(15,13),(15,14),(16,12)(16,13),(16,15),(16,14)有10种取法,所以概率.
(Ⅲ)把B组数据调整为,12,13,14,15,16,17,或12,13,14,15,16,17,,可见当或时,与A组数据方差相等.(可利用方差公式加以证明,但本题不需要)
考点:1、古典概型;2、样本的方差
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.从装有两个红球和两个白球的口袋内任取两个球,那么互斥而不对立的事件是( )
A.至少有一个白球与都是红球 B.恰好有一个白球与都是红球
C.至少有一个白球与都是白球 D.至少有一个白球与至少一个红球
2.抽样统计某校部分学生的物理测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A. B.
C. D.
3.给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②“当x为某一实数时,可使x2≤0”是不可能事件;③“明天天津市要下雨”是必然事件;④“从100个灯泡(含有10个次品)中取出5个,5个全是次品”是随机事件.
其中正确命题的个数是( )
A.0 B.1
C.2 D.3
4.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个容量为10的样本进行研究,则女同学甲被抽到的概率为( )
A. B. C. D.
5.口袋内有一些大小相同的红球、黄球和白球,从中任意摸出一球,摸出的球是红球或黄球的概率为0.4,摸出的球是红球或白球的概率为0.9,那么摸出的球是黄球或白球的概率为
A.0.7 B.0.5 C.0.3 D.0.6
6.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
A.91.5和91.5 B.91.5和92 C.91和91.5 D.92和92
7.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
A. B. C. D.
8.有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5,39.5) 7 [39.5,43.5) 3
根据样本的频率分布估计,大于或等于31.5的数据约占
A. B. C. D.
9.在5件产品中,有3件一等品和2件二等品,从中任取2件,以为概率的事件是( )
A.恰有1件一等品 B.至少有一件一等品
C.至多有一件一等品 D.都不是一等品
10.设有两组数据与,它们的平均数分别是和,则新的一组数据的平均数是
A. B. C. D.
11.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为元.
A.45 B.46 C. D.
12.甲、乙两位同学各拿出六张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是
A.甲得9张,乙得3张
B.甲得6张,乙得6张
C.甲得8张,乙得4张
D.甲得10张,乙得2张
13.某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各1人,则该小组数学成绩的平均数、众数、中位数分别为
A.85,85,85 B.87,85,86
C.87,85,85 D.87,85,90
14.从分别写有的张卡片中,任取张,这张上的字母恰好按字母顺序相邻的概率为( )
A. B. C. D.
15.某篮球运动员在最近几次参加的比赛中的得分情况如下表(没有罚球):
投篮次数 投中两分球的次数 投中三分球的次数
100 55 18
记该运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中不正确的是( )
A.P(A)=0.55 B.P(B)=0.18 C.P(C)=0.27 D.P(B+C)=0.55
二、填空题
16.某中学青年教师、中年教师和老年教师的人数比例为4∶5∶1,其中青年教师有120人.现采用分层抽样的方法从这所学校抽取容量为30的教师样本以了解教师的工作压力情况,则每位老年教师被抽到的概率为________.
17.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
学生 1号 2号 3号 4号 5号
甲班 6 7 7 8 7
乙班 6 7 6 7 9
则以上两组数据的方差中较小的一个为=____.
18.从字母中任取两个不同的字母,则取到字母的概率为_____________.
19.某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差___________________.
20.袋中装有大小相同的总数为个的黑球、白球若从袋中任意摸出个球,至少得到个白球的概率是,则从中任意摸出个球,得到的都是白球的概率为______.
三、解答题
21.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组,第二组,,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率;
(2)估计该校的800名男生的身高的平均数和中位数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x,y,事件,求.
22.某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
用户用水量频数直方图 用户用水量扇形统计图
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格.
23.某班的全体学生共有人,参加数学测试(百分制)成绩的频率分布直方图如图,数据的分组依次为:,,,. 依此表可以估计这一次测试成绩的中位数为分.
(1)求表中,的值;
(2)请估计该班本次数学测试的平均分.
24.对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 频数 频率
[10,15) 10 0.25
[15,20) 25 n
[20,25) m p
[25,30] 2 0.05
合计 M 1
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[10,15)内的人数.
25.海关对同时从三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
地区 A B C
数量/件 50 150 100
(1)求这6件样品中来自A,B,C三个地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
26.,两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
组:10,11,12,13,14,15,16
组:12,13,15,16,17,14,
假设所有病人的康复时间互相独立,从,两组随机各选1人,组选出的人记为甲,组选出的
人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ)当为何值时,,两组病人康复时间的方差相等?(结论不要求证明)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】列举每个事件所包含的基本事件,结合互斥事件和对立事件的定义,依次验证即可.
【详解】解:对于A,事件:“至少有一个白球”与事件:“都是红球”不能同时发生,但是对立,故A错误;
对于B,事件:“恰好有一个白球”与事件:“都是红球”不能同时发生,但从口袋内任取两个球时还有可能是两个都是白球,
所以两个事件互斥而不对立,故B正确;
对于C,事件:“至少有一个白球”与事件:“都是白球”可以同时发生,所以这两个事件不是互斥的,故C错误;
对于D,事件:“至少有一个白球”与事件:“至少一个红球”可以同时发生,即“一个白球,一个红球” ,所以这两个事件不是互斥的,故D错误.
故选:B.
2.D
【分析】根据频率分布直方图,求出不低于60分的频率即可得出答案
【详解】解:根据频率分布直方图,
不低于60分的频率为,
所以及格率是.
故选:D.
3.C
【解析】利用必然事件的概念可以判断①是正确的命题,③是偶然事件,利用不可能事件的概念判断②正确,利用随机事件的概念判断④正确.
【详解】对于①,三个球全部放入两个盒子,有两种情况:1+2和3+0,故必有一个盒子有一个以上的球,所以该事件是必然事件,①正确;
对于②,x=0时x2=0,所以该事件不是不可能事件,②错误;
对于③,“明天天津市要下雨”是偶然事件,所以该事件是随机事件,③错误;
对于④,“从100个灯泡(含有10个次品)中取出5个,5个全是次品”,发生与否是随机的,所以该事件是随机事件,④正确.故正确命题有2个.
故选:C.
4.C
【分析】根据古典概型特点判断,每个个体被抽到的概率都是等可能的,结合古典概型公式即可求解
【详解】由题知,从50个人抽10个,每个个体被抽取的概率都是等可能的,为,则女同学甲被抽到的概率也为
故选:C
【点睛】本题考查随机事件的概率,属于基础题
5.A
【分析】设摸出红球的概率为,摸出黄球的概率是,摸出白球的概率为,求出、的值,相加即可求解.
【详解】设摸出红球的概率为,摸出黄球的概率是,摸出白球的概率为,
所以,且,
所以,,
所以
【点睛】本题主要考查了互斥事件的概率加法公式的应用,其中解答中熟记互斥事件的概率加法公式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.
6.A
【详解】8个班参加合唱比赛的得分从小到大排列分别是87,89,90,91,92,93,94,96,中位数是91,92,的平均数91.5,平均数是=91.5
7.C
【详解】试题分析:由题意可知,事件A与事件B是相互独立的,而事件A、B中至少有一件发生的事件包含、、,又,,所以所事件的概率为,故选C.
考点:相互独立事件概率的计算.
8.B
【详解】由题意,该样本中大于或等于31.5的数据的频率为,
所以可估计大于或等于31.5的数据约占.
故选:B.
9.C
【分析】将件一等品编号为,件二等品的编号为,列举出从中任取件的所有基本事件的总数,分别计算选项的概率,即可得到答案.
【详解】将3件一等品编号为1,2,3,2件二等品编号为4,5,从中任取2件有10种取法:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).其中恰含有1件一等品的取法有:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),恰有1件一等品的概率为P1=,恰有2件一等品的取法有:(1,2),(1,3),(2,3).故恰有2件一等品的概率为P2=,其对立事件是“至多有一件一等品”,概率为P3=1-P2=1-=.
【点睛】本题主要考查了古典概型及其概率的计算问题,其中明确古典概型的基本概念,以及古典的概型及概率的计算公式,合理作出计算是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
10.B
【分析】由题意结合平均数的性质即可求得结果.
【详解】由题意结合平均数的性质可知:
的平均数为,
的平均数为,
则的平均数为:.
故选:B.
11.D
【详解】试题分析:根据中位数是把频率分布直方图分成面积相等的两部分的平行于y轴的直线横坐标,求出即可.
解:第一个矩形的面积是0.10,第二个矩形的面积是0.24,
第三个矩形的面积是0.36,第四个矩形的面积是1﹣0.70=0.30;
前面两个矩形的面积和是0.34,故将第三个矩形分成4:5即可,
∴中位数是40+×10=.
故选D.
考点:频率分布直方图.
12.A
【详解】试题分析:由题意可知:乙获得12张游戏牌概率为,所以甲应分得张牌,乙应分得张牌,故选A.
考点:排列组合问题.
13.C
【详解】由题意可知,学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各有1人,则该小组数学成绩的平均数,成绩排列为75,80,85,85,85,85,90,90,95,100,可得众数为85,中位数,因此选C
14.B
【分析】分别求出从张卡片中任取张的取法总数和字母相邻的种数,根据古典概型概率公式求得结果.
【详解】从张卡片中任取张,共有:种取法
其中字母相邻的有:,,,,共种情况
所求概率
本题正确选项:
【点睛】本题考查古典概型概率问题的求解,属于基础题.
15.D
【分析】结合概率的计算公式求得正确答案.
【详解】依题意,,
,
所以D选项结论不正确.
故选:D
16.
【解析】先利用人数比例和青年教师人数计算该校全部教师人数,再利用古典概型计算每位老年教师被抽到的概率即可.
【详解】由青年教师、中年教师和老年教师的人数比例为4∶5∶1, 知青年教师的人数比例为,故该校全部教师人数为:120÷=300(人).
采用分层抽样的方法从这所学校抽取容量为30的教师样本,则每位老年教师被抽到的概率为P==.
故答案为:.
17.
【详解】试题分析:甲班的方差较小,数据的平均值为7,
故方差s2==.
考点:本题主要考查平均数及方差的概念和计算.
点评:简单题,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
18./0.4
【分析】利用古典概型中的列举法,即可求得所求.
【详解】从字母中任取两个不同的字母的基本事件有、、、、、、、、、,共个,
其中 “取到字母”(记为事件)所包含的基本事件有、、、,共个,
故所求事件的概率为.
故答案为:0.4
19.
【详解】试题分析:由平均数及方差的定义可得;
.
考点:样本数据的数字特征:平均值与方差.
20.
【详解】因为袋中装有大小相同的总数为5个的黑球、白球,若从袋中任意摸出2个球,共有10种,没有得到白球的概率为,设白球个数为x,黑球个数为5-x,那么可知白球共有3个,黑球有2个,因此可知填写为
21.(1);(2)平均数为,中位数为;(3).
【分析】(1)由频率分布直方图的性质求第七组的频率;
(2)根据平均数和中位数的定义利用频率分布直方图求平均数和中位数;
(3)确定样本空间,利用古典概型概率公式求概率.
【详解】解:(1)第六组的频率为,
∴第七组的频率为.
(2)由直方图得,身高在第一组的频率为,
身高在第二组的频率为,
身高在第三组的频率为,
身高在第四组的频率为,
由于,,
设这所学校的800名男生的身高中位数为m,则,
由得,
所以这所学校的800名男生的身高的中位数为174.5cm,平均数为
.
(3)第六组的抽取人数为4,设所抽取的人为a,b,c,d,
第八组的抽取人数为,设所抽取的人为A,B,
则从中随机抽取两名男生有ab,ac,ad,bc,bd,cd,aA,aB,bA,bB,cA,cB,dA,dB,AB共15种情况,
因事件发生当且仅当随机抽取的两名男生在同一组,所以事件E包含的基本事件为ab,ac,ad,bc,bd,cd,AB共7种情况.所以.
22.(1)答案见解析;(2)答案见解析,79.2°;(3)4.08万户.
【解析】(1)根据用户用水量在吨的户数以及所占比例得出样本容量;
(2)由样本容量减去用水15~20吨之外的户数,即可得出用水15~20吨的户数,再由用水15~20吨的户数占样本容量的比例求出圆心角;
(3)将样本中享受基本价格的户数所占样本的比例乘以得出答案.
【详解】(1);
(2)用水15~20吨的户数为100-10-36-24-8=22(户),
“15~20吨”部分的圆心角的度数为
(3)(万户)
所以该地区6万用户中约有4.08万户的用水全部享受基本价格.
23.(1),;(2)分.
【解析】(1)利用中位数为解得,然后利用频率和为求解;
(2)利用每个区间的中点值乘以该组的频率求和即可得到答案.
【详解】(1)由中位数为70可得,
,
解得.
又,
解得.
(2)由频率分布直方图可知,每组的频率依次为:,,,,则该班本次数学测试的平均分的估计值为:分.
【点睛】利用频率分布直方图估计样本的中位数及平均值的方法如下:
(1)平均数的估计值等于各小矩形面积乘以底边中点的横坐标之和;
(2)中位数的估计值等于把频率分布直方图分成面积相等的两部分时,分界线与横轴交点的横坐标.
24.(1)M=40,,;(2)90人.
【解析】(1)根据频数与频率的统计表和频率分布直方图计算可得结果;
(2)根据频数样本容量频率可求得结果.
【详解】(1)由[10,15)内的频数是10,频率是0.25知,,所以M=40.
因为频数之和为40,所以10+25+m+2=40,m=3..
因为a是对应分组[15,20)的频率与组距的商,所以.
(2)因为该校高一学生有360人,分组[10,15)内的频率是0.25,所以估计该校高一学生参加社区服务的次数在此区间内的人数为90人.
【点睛】关键点点睛:根据频数与频率的统计表和频率分布直方图计算求解是解题关键.
25.(1)1,3,2;(2).
【解析】(1)由分层抽样的性质运算即可得解;
(2)利用列举法,结合古典概型概率的计算公式,即可得解.
【详解】(1)由题意,样品中来自A地区商品的数量为,
来自B地区商品的数量为,
来自C地区商品的数量为;
(2)设来自地区的样品编号为,来自地区的样品编号为,,,
来自地区的样品编号为,,
则从6件样品中抽取2件产品的所有基本事件为:
,,,,,,,,
,,,,,,,共15个;
抽取的这2件产品来自相同地区的基本事件有:
,,,,共4个;
故所求概率.
【点睛】本题考查了分层抽样的应用及古典概型概率的求解,考查了运算求解能力,属于中档题.
26.(Ⅰ),(Ⅱ),(Ⅲ)或
【详解】试题分析:针对甲有7种情况,康复时间不少于14天有3种情况,概率为;如果,甲、乙随机各取一人有49种情况,用列举法列出甲的康复时间比乙的康复时间长的情况有10种,概率为,由于A组数据为10,11,12,13,14,15,16;B组数据调整为,12,13,14,15,16,17,或12,13,14,15,16,17,,由于,两组病人康复时间的方差相等,即波动相同,所以或.
试题解析:(Ⅰ)甲有7种取法,康复时间不少于14天的有3种取法,所以概率;
(Ⅱ) 如果,从,两组随机各选1人,组选出的人记为甲,组选出的人记为乙共有49种取法,甲的康复时间比乙的康复时间长的列举如下:(13,12),(14,12),(14,13),(15,12),(15,13),(15,14),(16,12)(16,13),(16,15),(16,14)有10种取法,所以概率.
(Ⅲ)把B组数据调整为,12,13,14,15,16,17,或12,13,14,15,16,17,,可见当或时,与A组数据方差相等.(可利用方差公式加以证明,但本题不需要)
考点:1、古典概型;2、样本的方差
答案第1页,共2页
答案第1页,共2页
