第5章5.4统计与概率的应用 同步练习(含解析)
文档属性
| 名称 | 第5章5.4统计与概率的应用 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 853.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-14 00:00:00 | ||
图片预览




文档简介
第5章5.4统计与概率的应用同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为.那么以下理解正确的是( )
A.某顾客抽奖10次,一定能中奖1次
B.某顾客抽奖10次,可能1次也没中奖
C.某顾客消费210元,一定不能中奖
D.某顾客消费1000元,至少能中奖1次
2.甲、乙两人参加“社会主义价值观”知识竞赛,甲、乙两人的能荣获一等奖的概率分别为和,甲、乙两人是否获得一等奖相互独立,则这两个人中恰有一人获得一等奖的概率为( )
A. B. C. D.
3.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
4.根据某市疾控中心的健康监测,该市在校中学生的近视率约为78.7%.某眼镜厂商要到中学给近视学生配送滴眼液,每人一瓶,已知该校学生总数为600人,则眼镜商应带滴眼液的瓶数为( )
A.600 B.787 C.不少于473 D.不多于473
5.调查运动员服用兴奋剂的时候,应用Warner随机化应答方法调查300名运动员,得到80个“是”的回答,由此,我们估计服用过兴奋剂的人占这群人中回答此问题人的( )
A.3.33% B.53% C.5% D.26%
6.从一群玩游戏的小孩中抽出k人,一人分一个苹果,让他们返回继续玩游戏,一会儿后,再从中任取m人,发现其中有n个小孩曾分过苹果,估计共有小孩( )
A.人 B.人 C.人 D.人
7.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. B. C. D.
8.某比赛为甲、乙两名运动员制订下列发球规则:规则一:投掷一枚硬币,出现正面向上,甲发球,否则乙发球;规则二:从装有个红球与个黑球的布袋中随机地取出个球,如果同色,甲发球,否则乙发球;规则三:从装有个红球与个黑球的布袋中随机地取出个球,如果同色,甲发球,否则乙发球.
其中对甲、乙公平的规则是( )
A.规则一和规则二 B.规则一和规则三 C.规则二和规则三 D.规则二
9.先将一个棱长为的正方体木块的六个面分别涂上颜色,再将该正方体均匀切割成棱长为的小正方体,现从切好的小正方体中任取一块,所得小正方体恰有一面涂有颜色的概率是( )
A. B. C. D.
10.某种彩票中奖的概率为,这是指
A.买10000张彩票一定能中奖
B.买10000张彩票只能中奖1次
C.若买9999张彩票未中奖,则第10000张必中奖
D.买一张彩票中奖的可能性是
11.现有张牌面分别是,,,,,的扑克牌,从中取出张,记下牌面上的数字后放回,再取一张记下牌面上的数字,则两次所记数字之和能整除的概率是
A. B. C. D.
12.小明准备参加电工资格考试,先后进行理论考试和操作考试两个环节,每个环节各有2次考试机会,在理论考试环节,若第一次考试通过,则直接进入操作考试;若第一次未通过,则进行第2次考试,第2次考试通过后进入操作考试环节,第2次未通过则直接被淘汰.在操作考试环节,若第1次考试通过,则直接获得证书;若第1次未通过,则进行第2次考试,第2次考试通过后获得证书,第2次未通过则被淘汰.若小明每次理论考试通过的概率为,每次操作考试通过的概率为,并且每次考试相互独立,则小明本次电工考试中共参加3次考试的概率是
A. B. C. D.
13.某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下:
行业名称 计算机 机械 营销 物流 贸易
应聘人数 215830 200250 154676 74570 65280
行业名称 计算机 营销 机械 建筑 化工
招聘人数 124620 102935 89115 76516 70436
若用同一行业中应聘人数和招聘人数的比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是( )
A.计算机行业好于化工行业 B.建筑行业好于物流行业
C.机械行业最紧张 D.营销行业比贸易行业紧张
14.某地某年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是
A.计算机行业好于化工行业. B.建筑行业好于物流行业.
C.机械行业最紧张. D.营销行业比贸易行业紧张.
15.七巧板,又称七巧图、智慧板,是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,于明、清两代在民间广泛流传.某同学用边长为4 dm的正方形木板制作了一套七巧板,如图所示,包括5个等腰直角三角形,1个正方形和1个平行四边形.若该同学从5个三角形中任取出2个,则这2个三角形的面积之和不小于另外3个三角形面积之和的概率是( )
A. B. C. D.
二、填空题
16.设有外形完全相同的两个箱子,甲箱中有99个白球,1个黑球,乙箱中有1个白球,99个黑球.随机地抽取一箱,再从取出的一箱中抽取一球,结果取得白球,我们可以认为这球是从_____箱中取出的.
17.若样本数据是以频率分布直方图的形式给出,这时已不存在原始数据,因此要确定其p%分位数,只能估算,其p%分位数即为频率分布直方图中使左侧小矩形面积之和等于p%的分点值.
例如:若某校100名学生的数学测试成绩的频率分布直方图如图:则可估计其80%分位数为_____.
18.博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为,则______.
19.在一场对抗赛中,两人争夺冠军,若比赛采用“五局三胜制”,每局获胜的概率均为,且各局比赛相互独立,则在第一局失利的情况下,经过五局比赛最终获得冠军的概率是_____.
20.某校组织“中国诗词”竞赛,在“风险答题”的环节中,共为选手准备了三类不同的题目,选手每答对一个类、类或类的题目,将分别得到分,分,分,但如果答错,则相应要扣去分,分,分,根据平时训练经验,选手甲答对类、类或类的题目的概率分别为、、,若要每一次答题的均分更大一些,则选手甲应选择的题目类型应为_________.(填,或)
三、解答题
21.已知是一个三位正整数,若的个位数字大于十位数字,十位数字大于百位数字,则称为“三位递增数”(如135,256,345等).现要从甲、乙两名同学中选出人参加某市组织的数学竞赛,选取的规则如下:从由1,2,3,4,5,6组成的所有“三位递增数”中随机抽取1个数,若抽取的“三位递增数”是偶数,则甲参加数学竞赛;否则,乙参加数学竞赛.
(1)由1,2,3,4,5,6可组成多少个“三位递增数”?分别用树状图法和列举法解答.
(2)这种选取规则对甲、乙两名同学公平吗?请说明理由.
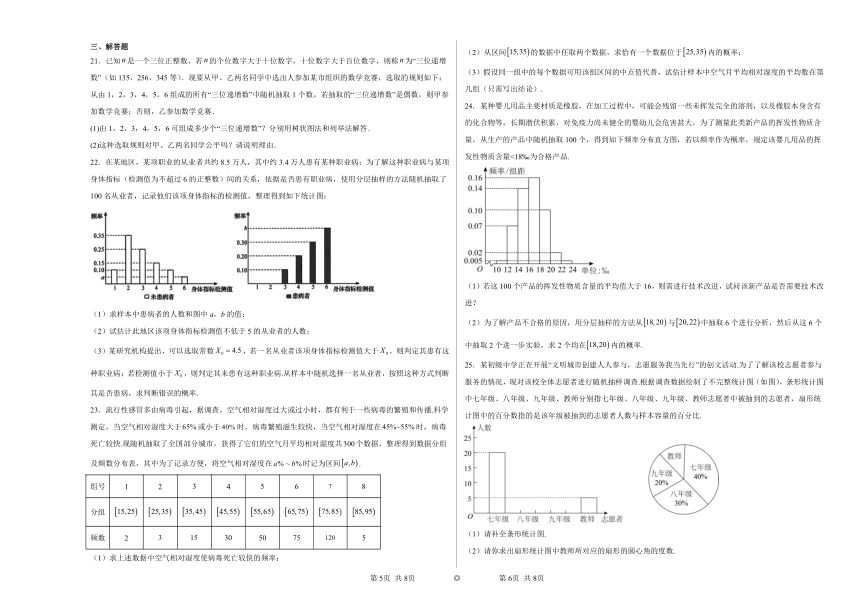
22.在某地区,某项职业的从业者共约8.5万人,其中约3.4万人患有某种职业病:为了解这种职业病与某项身体指标(检测值为不超过6的正整数)间的关系,依据是否患有职业病,使用分层抽样的方法随机抽取了100名从业者,记录他们该项身体指标的检测值,整理得到如下统计图:
(1)求样本中患病者的人数和图中a,b的值;
(2)试估计此地区该项身体指标检测值不低于5的从业者的人数;
(3)某研究机构提出,可以选取常数,若一名从业者该项身体指标检测值大于,则判定其患有这种职业病;若检测值小于,则判定其未患有这种职业病.从样本中随机选择一名从业者,按照这种方式判断其是否患病,求判断错误的概率.
23.流行性感冒多由病毒引起,据调查,空气相对湿度过大或过小时,都有利于一些病毒的繁殖和传播.科学测定,当空气相对湿度大于或小于时,病毒繁殖滋生较快,当空气相对湿度在时,病毒死亡较快.现随机抽取了全国部分城市,获得了它们的空气月平均相对湿度共个数据,整理得到数据分组及频数分布表,其中为了记录方便,将空气相对湿度在时记为区间.
组号
分组
频数
(1)求上述数据中空气相对湿度使病毒死亡较快的频率;
(2)从区间的数据中任取两个数据,求恰有一个数据位于内的概率;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中空气月平均相对湿度的平均数在第几组(只需写出结论).
24.某种婴儿用品主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,为了测量此类新产品的挥发性物质含量,从生产的产品中随机抽取100个,得到如下频率分布直方图,若以频率作为概率,规定该婴儿用品的挥发性物质含量<18‰为合格产品.
(1)若这100个产品的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求2个均在内的概率.
25.某初级中学正在开展“文明城市创建人人参与,志愿服务我当先行”的创文活动.为了了解该校志愿者参与服务的情况,现对该校全体志愿者进行随机抽样调查.根据调查数据绘制了不完整统计图(如图),条形统计图中七年级、八年级、九年级、教师分别指七年级、八年级、九年级、教师志愿者中被抽到的志愿者,扇形统计图中的百分数指的是该年级被抽到的志愿者人数与样本容量的百分比.
(1)请补全条形统计图.
(2)请你求出扇形统计图中教师所对应的扇形的圆心角的度数.
(3)若该校共有志愿者人,则该校七年级大约有多少名志愿者?
26.甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为,甲、丙两台机床加工的零件都是一等品的概率为.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【解析】根据概率的定义进行判断.
【详解】解:中奖概率表示每一次抽奖中奖的可能性都是,
故不论抽奖多少次,都可能一次也不中奖,
故选:B.
【点睛】此题考查对概率定义的理解,属于基础题
2.D
【分析】利用相互独立事件概率计算公式,计算出所求概率.
【详解】设甲、乙获一等奖的概率分别是,不获一等奖的概率是,则这两人中恰有一人获奖的事件的概率为:.
故选:D
【点睛】本小题主要考查相互独立事件概率计算,属于基础题.
3.C
【分析】根据所给的六大素养雷达图逐个分析即可.
【详解】A选项,甲的数据分析素养为分, 乙的数据分析素养为分, 乙的数据分析素养低于甲,选项错误;
B选项,乙的数学建模素养为分, 乙的数学抽象为素养分,选项错误;
C选项, 甲的六大素养指标值分别为,,,,,;乙的六大素养指标值分别为,,,,,,甲的六大素养指标值波动性比乙小,选项正确;
D选项,由C可知,甲的六大素养中,数学抽象,数学建模和数学运算最差,直观想象最最好,选项错误;
故选C.
【点睛】本题考查了命题真假的判断以及统计图雷达图的识别和应用,考查学生简单的推理,属于基础题.
4.C
【解析】根据近视率估计有多少人得了近视即可得解;
【详解】解:依题意,该市在校中学生的近视率约为78.7%.
故600人中大约有
故眼镜商应带滴眼液的瓶数应不少于473瓶
故选:
【点睛】本题考查概率的应用,属于基础题.
5.A
【解析】根据Warner随机化应答方法调查计算出服用兴奋剂的人大约有几人,再根据古典概型的概率计算公式计算可得.
【详解】解:应用Warner随机化应答方法调查300名运动员,我们期望有150人回答了第一个问题,而这150人中又大约一半的人即75人回答了“是”,其余5个回答“是”的人服用过兴奋剂,由此估计这群人中服用兴奋剂大约占,
故选:
【点睛】本题考查Warner随机化应答方法调查,概率的应用,属于基础题.
6.B
【解析】本题是一个情景问题,由问题描述知个小孩在总体中所占的比例是,由此比例关系计算出总共多少人选出正确选项.
【详解】解:由题意,个小孩在总体中所点的比例是,
故总体的人数是.
故选:.
【点睛】本题考查随机抽样和概率知识的应用,理解题意,由题中描述得出个小孩在总体中所点的比例是解题的关键,本题是实际背景的情景的问题,要注意与抽样中样本与总体这些术语的对应,从而得到计算方法.
7.A
【解析】先求出基本事件总数,再求出田忌的马获胜包含的基本事件种数,由此能求出田忌的马获胜的概率.
【详解】分别用A,B,C表示齐王的上、中、下等马,用a,b,c表示田忌的上、中、下等马,现从双方的马匹中随机选一匹进行一场比赛有Aa,Ab,Ac,Ba,Bb,Bc,Ca,Cb,Cc共9场比赛,其中田忌马获胜的有Ba,Ca,Cb共3场比赛,所以田忌马获胜的概率为.
故选:A.
【点睛】本题考查概率的求法,考查等可能事件概率计算公式等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
8.B
【分析】计算出三种规则下甲发球和乙发球的概率,当两人发球的概率均为时,该规则对甲、乙公平,由此可得出正确选项.
【详解】对于规则一,每人发球的机率都是,是公平的;
对于规则二,记个红球分别为红,红,个黑球分别为黑、黑,
则随机取出个球的所有可能的情况有(红,红),(红,黑),(红,黑),(红,黑),(红,黑),(黑,黑),共种,其中同色的情况有种,
所以甲发球的可能性为,不公平;
对于规则三,记个红球分别为红、红、红,则随机取出个球所有可能的情况有(红,红),(红,红),(红,黑),(红,红),(红,黑),(红,黑),共种,其中同色的情况有种,所以两人发球的可能性均为,是公平的.
因此,对甲、乙公平的规则是规则一和规则三.
故选B.
【点睛】本题考查利用规则的公平性问题,同时也考查了利用古典概型的概率公式计算事件的概率,正确理解题意是解题的关键,考查计算能力,属于中等题.
9.A
【分析】计算出小正方体的个数,并数出恰有一面涂有颜色的小正方体的个数,利用古典概型概率公式即可计算出所求事件的概率.
【详解】将棱长为的正方体均匀切割成棱长为的小正方体,一共可切割成块,而只有位于大正方体的各个面中心的小正方体恰有一面涂有颜色,共块,
因此,所得小正方体恰有一面涂有颜色的概率是.
故选A.
【点睛】本题考查利用古典概型概率公式计算所求事件的概率,考查计算能力,属于基础题.
10.D
【分析】彩票中奖的概率为,只是指中奖的可能性为
【详解】彩票中奖的概率为,只是指中奖的可能性为,
不是买10000张彩票一定能中奖,
概率是指试验次数越来越大时,频率越接近概率.所以选D.
【点睛】概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,是否中奖是随机事件.
11.D
【详解】由题意,试验的情况总数有,
又,即两次所记数字之和能整除的有:
,,,两次交换顺序共8种,还有,
即所求事件个数共有,所以所求概率为.
故选:D.
12.B
【详解】试题分析:设小明本次电工考试中共参加3次考试为事件,小明本次电工考试中第一次理论考试没通过,第二次理论考试通过,第一次操作考试通过为事件,小明本次电工考试中第一次理论考试通过,第一次操作考试没通过,第二次操作考试通过为事件,则,而,,所以,故应填.
考点:1、独立事件的概率公式;
13.B
【详解】试题分析:就业形势的好坏,主要看招聘人数与应聘人数的比值,比值越大,就业形势越好,故选B.
考点:本题主要考查不等式的概念、不等式的性质.
点评:解答此类题目,首先要审清题意,明确就业形势的好坏,主要看招聘人数与应聘人数的比值.
14.B
【详解】∵用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,
∴建筑行业招聘人数是76516,而应聘人数没有排在前五位,小于65280,
建筑行业人才是供不应求,
∵物流行业应聘人数是74570,
而招聘人数不在前五位,要小于70436,
∴物流行业是供大于求,
∴就业形势是建筑行业好于物流行业,
故选B.
15.D
【分析】先逐个求解所有5个三角形的面积,再根据要求计算概率.
【详解】如图所示,,,,,的面积分别为,,.
将,,,,分别记为,,,,,从这5个三角形中任取出2个,则样本空间,共有10个样本点.
记事件表示“从5个三角形中任取出2个,这2个三角形的面积之和不小于另外3个三角形面积之和”,则事件包含的样本点为,,,共3个,所以.
故选:D.
16.甲.
【解析】分别求出甲箱中取到白球的概率和乙箱中取到白球的概率,由此进行判断.
【详解】解:甲箱有99个白球1个黑球,
随机地取出一球,得白球的可能性是,
乙箱中有1个白球和99个黑球,从中任取一球,得白球的可能性是,
由此看到,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.
既然在一次抽样中抽得白球,当然可以认为是由概率大的箱子中抽出的.
我们作出推断是从甲箱中抽出的.
故答案为:甲
【点睛】本题考查概率的应用,属于基础题,解题时要认真审题,注意概率的计算.
17.133.3.
【解析】根据分位数的定义计算可得.
【详解】解析:分数在130以下的学生所占比例为.
在140以下的学生所占比例为.
因此,80%分位数一定位于内,由.
可以估计80%分位数为133.3.
答案:133.3.
【点睛】本题考查分位数的概念,属于基础题.
18.
【分析】利用列举法求出方案一坐到“3号”车的概率为,利用古典概型求出方案二坐到“3号”车的概率为,由此能求出结果
【详解】三辆车的出车顺序可能为:123、132、213、231、312、321
方案一坐车可能:132、213、231,所以,;
方案二坐车可能:312、321,所以,;
所以,
答案:
【点睛】本题考查概率的计算,属于基础题
19..
【分析】第一局失利,最终经过5局比赛获得冠军,说明第2,3,4局胜2局,胜1局,根据相互独立事件的概率公式计算即可.
【详解】第1局失利为事实,经过5局获胜,第2,3,4局胜2局,胜1局,5局比赛最终获得冠军的概率是.
【点睛】本题主要考查了相互独立事件的概率乘法公式,属于中档题.
20.
【详解】选手甲选择A类题目,得分的均值为:
0.6×300+0.4×( 300)=60,
选手甲选择B类题目,得分的均值为:
0.75×200+0.25×( 200)=100,
选手甲选择C类题目,得分的均值为:
0.85×100+0.15×( 100)=70,
∴若要每一次答题的均分更大一些,
则选手甲应选择的题目类型应为B.
故答案为:B.
21.(1)答案见解析
(2)对甲、乙两名同学不公平,理由见解析.
【详解】(1)树状图法:画出树状图,如图所示:
从上面的树状图,知由1,2,3,4,5,6可组成20个“三位递增数”;
列举法:由题意,知由1,2,3,4,5,6组成的“三位递增数”分别是123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456,
共20个,故由1,2,3,4,5,6可组成20个“三位递增数”.
(2)不公平.理由如下:
由(1),知由1,2,3,4,5,6组成的“三位递增数”有20个记“甲参加数学竞赛”为事件,事件包含的样本点有124,126,134,136,146,156,234,236,246,256,346,356,456,共13个.
所以.
记“乙参加数学竞赛”为事件,则事件包含的样本点有123,125,135,145,235,245,345,共7个.
所以.因为,
所以该选取规则对甲、乙两名同学不公平.
22.(1)患病者的人数为40,,;(2)31450;(3).
【分析】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为40人,由此能求出,.
(2)指标检测值不低于5的样本中,有患病者28人,未患病者9人,共37人,此地区该项身体指标检测值不低于5的从业者的人数.
(3)当时,在100个样本数据中,有12名患病者被误判为未患病,有9名未患病者被误判为患病者,由此能判断错误的概率.
【详解】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为.
,.
(2)由(1)可知,患病者的人数为,未患病的人数为,该项身体指标检测值不低于5的样本中,有患病者(人),未患病者(人),共37人.
故估计此地区该项身体指标检测值不低于5的从业者的人数为.
(3)当时,在100个样本数据中,有(名)患病者被误判为未患病,有(名)未患病者被误判为患病,
因此判断错误的概率为.
23.(1);(2);(3)第组.
【分析】(1)利用样本在上的频数除以可得所求频率;
(2)设区间中的两个数据为、,区间中的三个数据为、、,列举出所有的基本事件,并确定所求事件所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率;
(3)计算出样本的平均数,可得出结论.
【详解】(1)由已知,当空气相对湿度在时,病毒死亡较快.
而样本在上的频数为,所以所求频率为;
(2)设事件为“从区间的数据中任取两个数据,恰有一个数据位于内”,
设区间中的两个数据为、,区间中的三个数据为、、,
因此,从区间的数据中任取两个数据,
包含、、、、、、、、、,共个样本点,
而事件包含、、、、、,共个样本点,所以;
(3)样本的平均数为,
故样本的平均数在第组.
24.(1)该产品需要进行技术改进;(2).
【分析】(1)、由频率分布直方图求出平均值判断与16的大小关系即可得出结论;
(2)、先根据分层抽样求得在与中所抽取的个数,运用列举法列出事件的所有情况,由古典概率公式可求得答案.
【详解】(1)∵,故该产品需要进行技术改进;
(2)组的产品的个数为,组的产品的个数,所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为,组中抽取的一个为,
则从6个中抽取2个的所有情况如下:共15种情况,
其中在中恰有2个的有共10种情况,所以所求的概率.
25.(1)条形统计图见解析;(2);(3)名.
【分析】(1)本题首先可根据题意求出样本容量、八年级志愿者被抽到的人数以及九年级志愿者被抽到的人数,然后补全条形统计图即可;
(2)可根据教师志愿者被抽到的人数所占百分比求出对应的圆心角的度数;
(3)可通过总人数以及七年级志愿者所占比例得出结果.
【详解】(1)由题意知样本容量为,
则八年级志愿者被抽到的人数为,
九年级志愿者被抽到的人数为,
补全条形统计图如下:
(2)因为教师志愿者被抽到的人数所占百分比为,
所以对应的扇形的圆心角的度数为.
(3)(名),该校七年级大约有240名志愿者.
【点睛】本题考查条形统计图以及扇形统计图的实际应用,考查如何补全条形统计图,考查条形统计图以及扇形统计图之间的关系,考查计算能力,是简单题.
26.(1),,;(2)
【分析】(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,则再利用独立事件的概率计算公式,解方程组即可得到答案.
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,利用对立事件,即计算即可.
【详解】(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,
由题设条件有即
解得,,.
即甲、乙、丙三台机床各自加工的零件是一等品的概率分别是,,;
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,则
.
故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为.
【点晴】本题主要考查独立事件的概率计算问题,涉及到对立事件的概率计算,考查学生的数学运算能力,是一道容易题.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为.那么以下理解正确的是( )
A.某顾客抽奖10次,一定能中奖1次
B.某顾客抽奖10次,可能1次也没中奖
C.某顾客消费210元,一定不能中奖
D.某顾客消费1000元,至少能中奖1次
2.甲、乙两人参加“社会主义价值观”知识竞赛,甲、乙两人的能荣获一等奖的概率分别为和,甲、乙两人是否获得一等奖相互独立,则这两个人中恰有一人获得一等奖的概率为( )
A. B. C. D.
3.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
4.根据某市疾控中心的健康监测,该市在校中学生的近视率约为78.7%.某眼镜厂商要到中学给近视学生配送滴眼液,每人一瓶,已知该校学生总数为600人,则眼镜商应带滴眼液的瓶数为( )
A.600 B.787 C.不少于473 D.不多于473
5.调查运动员服用兴奋剂的时候,应用Warner随机化应答方法调查300名运动员,得到80个“是”的回答,由此,我们估计服用过兴奋剂的人占这群人中回答此问题人的( )
A.3.33% B.53% C.5% D.26%
6.从一群玩游戏的小孩中抽出k人,一人分一个苹果,让他们返回继续玩游戏,一会儿后,再从中任取m人,发现其中有n个小孩曾分过苹果,估计共有小孩( )
A.人 B.人 C.人 D.人
7.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. B. C. D.
8.某比赛为甲、乙两名运动员制订下列发球规则:规则一:投掷一枚硬币,出现正面向上,甲发球,否则乙发球;规则二:从装有个红球与个黑球的布袋中随机地取出个球,如果同色,甲发球,否则乙发球;规则三:从装有个红球与个黑球的布袋中随机地取出个球,如果同色,甲发球,否则乙发球.
其中对甲、乙公平的规则是( )
A.规则一和规则二 B.规则一和规则三 C.规则二和规则三 D.规则二
9.先将一个棱长为的正方体木块的六个面分别涂上颜色,再将该正方体均匀切割成棱长为的小正方体,现从切好的小正方体中任取一块,所得小正方体恰有一面涂有颜色的概率是( )
A. B. C. D.
10.某种彩票中奖的概率为,这是指
A.买10000张彩票一定能中奖
B.买10000张彩票只能中奖1次
C.若买9999张彩票未中奖,则第10000张必中奖
D.买一张彩票中奖的可能性是
11.现有张牌面分别是,,,,,的扑克牌,从中取出张,记下牌面上的数字后放回,再取一张记下牌面上的数字,则两次所记数字之和能整除的概率是
A. B. C. D.
12.小明准备参加电工资格考试,先后进行理论考试和操作考试两个环节,每个环节各有2次考试机会,在理论考试环节,若第一次考试通过,则直接进入操作考试;若第一次未通过,则进行第2次考试,第2次考试通过后进入操作考试环节,第2次未通过则直接被淘汰.在操作考试环节,若第1次考试通过,则直接获得证书;若第1次未通过,则进行第2次考试,第2次考试通过后获得证书,第2次未通过则被淘汰.若小明每次理论考试通过的概率为,每次操作考试通过的概率为,并且每次考试相互独立,则小明本次电工考试中共参加3次考试的概率是
A. B. C. D.
13.某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下:
行业名称 计算机 机械 营销 物流 贸易
应聘人数 215830 200250 154676 74570 65280
行业名称 计算机 营销 机械 建筑 化工
招聘人数 124620 102935 89115 76516 70436
若用同一行业中应聘人数和招聘人数的比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是( )
A.计算机行业好于化工行业 B.建筑行业好于物流行业
C.机械行业最紧张 D.营销行业比贸易行业紧张
14.某地某年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是
A.计算机行业好于化工行业. B.建筑行业好于物流行业.
C.机械行业最紧张. D.营销行业比贸易行业紧张.
15.七巧板,又称七巧图、智慧板,是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,于明、清两代在民间广泛流传.某同学用边长为4 dm的正方形木板制作了一套七巧板,如图所示,包括5个等腰直角三角形,1个正方形和1个平行四边形.若该同学从5个三角形中任取出2个,则这2个三角形的面积之和不小于另外3个三角形面积之和的概率是( )
A. B. C. D.
二、填空题
16.设有外形完全相同的两个箱子,甲箱中有99个白球,1个黑球,乙箱中有1个白球,99个黑球.随机地抽取一箱,再从取出的一箱中抽取一球,结果取得白球,我们可以认为这球是从_____箱中取出的.
17.若样本数据是以频率分布直方图的形式给出,这时已不存在原始数据,因此要确定其p%分位数,只能估算,其p%分位数即为频率分布直方图中使左侧小矩形面积之和等于p%的分点值.
例如:若某校100名学生的数学测试成绩的频率分布直方图如图:则可估计其80%分位数为_____.
18.博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为,则______.
19.在一场对抗赛中,两人争夺冠军,若比赛采用“五局三胜制”,每局获胜的概率均为,且各局比赛相互独立,则在第一局失利的情况下,经过五局比赛最终获得冠军的概率是_____.
20.某校组织“中国诗词”竞赛,在“风险答题”的环节中,共为选手准备了三类不同的题目,选手每答对一个类、类或类的题目,将分别得到分,分,分,但如果答错,则相应要扣去分,分,分,根据平时训练经验,选手甲答对类、类或类的题目的概率分别为、、,若要每一次答题的均分更大一些,则选手甲应选择的题目类型应为_________.(填,或)
三、解答题
21.已知是一个三位正整数,若的个位数字大于十位数字,十位数字大于百位数字,则称为“三位递增数”(如135,256,345等).现要从甲、乙两名同学中选出人参加某市组织的数学竞赛,选取的规则如下:从由1,2,3,4,5,6组成的所有“三位递增数”中随机抽取1个数,若抽取的“三位递增数”是偶数,则甲参加数学竞赛;否则,乙参加数学竞赛.
(1)由1,2,3,4,5,6可组成多少个“三位递增数”?分别用树状图法和列举法解答.
(2)这种选取规则对甲、乙两名同学公平吗?请说明理由.
22.在某地区,某项职业的从业者共约8.5万人,其中约3.4万人患有某种职业病:为了解这种职业病与某项身体指标(检测值为不超过6的正整数)间的关系,依据是否患有职业病,使用分层抽样的方法随机抽取了100名从业者,记录他们该项身体指标的检测值,整理得到如下统计图:
(1)求样本中患病者的人数和图中a,b的值;
(2)试估计此地区该项身体指标检测值不低于5的从业者的人数;
(3)某研究机构提出,可以选取常数,若一名从业者该项身体指标检测值大于,则判定其患有这种职业病;若检测值小于,则判定其未患有这种职业病.从样本中随机选择一名从业者,按照这种方式判断其是否患病,求判断错误的概率.
23.流行性感冒多由病毒引起,据调查,空气相对湿度过大或过小时,都有利于一些病毒的繁殖和传播.科学测定,当空气相对湿度大于或小于时,病毒繁殖滋生较快,当空气相对湿度在时,病毒死亡较快.现随机抽取了全国部分城市,获得了它们的空气月平均相对湿度共个数据,整理得到数据分组及频数分布表,其中为了记录方便,将空气相对湿度在时记为区间.
组号
分组
频数
(1)求上述数据中空气相对湿度使病毒死亡较快的频率;
(2)从区间的数据中任取两个数据,求恰有一个数据位于内的概率;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中空气月平均相对湿度的平均数在第几组(只需写出结论).
24.某种婴儿用品主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,为了测量此类新产品的挥发性物质含量,从生产的产品中随机抽取100个,得到如下频率分布直方图,若以频率作为概率,规定该婴儿用品的挥发性物质含量<18‰为合格产品.
(1)若这100个产品的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求2个均在内的概率.
25.某初级中学正在开展“文明城市创建人人参与,志愿服务我当先行”的创文活动.为了了解该校志愿者参与服务的情况,现对该校全体志愿者进行随机抽样调查.根据调查数据绘制了不完整统计图(如图),条形统计图中七年级、八年级、九年级、教师分别指七年级、八年级、九年级、教师志愿者中被抽到的志愿者,扇形统计图中的百分数指的是该年级被抽到的志愿者人数与样本容量的百分比.
(1)请补全条形统计图.
(2)请你求出扇形统计图中教师所对应的扇形的圆心角的度数.
(3)若该校共有志愿者人,则该校七年级大约有多少名志愿者?
26.甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为,甲、丙两台机床加工的零件都是一等品的概率为.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【解析】根据概率的定义进行判断.
【详解】解:中奖概率表示每一次抽奖中奖的可能性都是,
故不论抽奖多少次,都可能一次也不中奖,
故选:B.
【点睛】此题考查对概率定义的理解,属于基础题
2.D
【分析】利用相互独立事件概率计算公式,计算出所求概率.
【详解】设甲、乙获一等奖的概率分别是,不获一等奖的概率是,则这两人中恰有一人获奖的事件的概率为:.
故选:D
【点睛】本小题主要考查相互独立事件概率计算,属于基础题.
3.C
【分析】根据所给的六大素养雷达图逐个分析即可.
【详解】A选项,甲的数据分析素养为分, 乙的数据分析素养为分, 乙的数据分析素养低于甲,选项错误;
B选项,乙的数学建模素养为分, 乙的数学抽象为素养分,选项错误;
C选项, 甲的六大素养指标值分别为,,,,,;乙的六大素养指标值分别为,,,,,,甲的六大素养指标值波动性比乙小,选项正确;
D选项,由C可知,甲的六大素养中,数学抽象,数学建模和数学运算最差,直观想象最最好,选项错误;
故选C.
【点睛】本题考查了命题真假的判断以及统计图雷达图的识别和应用,考查学生简单的推理,属于基础题.
4.C
【解析】根据近视率估计有多少人得了近视即可得解;
【详解】解:依题意,该市在校中学生的近视率约为78.7%.
故600人中大约有
故眼镜商应带滴眼液的瓶数应不少于473瓶
故选:
【点睛】本题考查概率的应用,属于基础题.
5.A
【解析】根据Warner随机化应答方法调查计算出服用兴奋剂的人大约有几人,再根据古典概型的概率计算公式计算可得.
【详解】解:应用Warner随机化应答方法调查300名运动员,我们期望有150人回答了第一个问题,而这150人中又大约一半的人即75人回答了“是”,其余5个回答“是”的人服用过兴奋剂,由此估计这群人中服用兴奋剂大约占,
故选:
【点睛】本题考查Warner随机化应答方法调查,概率的应用,属于基础题.
6.B
【解析】本题是一个情景问题,由问题描述知个小孩在总体中所占的比例是,由此比例关系计算出总共多少人选出正确选项.
【详解】解:由题意,个小孩在总体中所点的比例是,
故总体的人数是.
故选:.
【点睛】本题考查随机抽样和概率知识的应用,理解题意,由题中描述得出个小孩在总体中所点的比例是解题的关键,本题是实际背景的情景的问题,要注意与抽样中样本与总体这些术语的对应,从而得到计算方法.
7.A
【解析】先求出基本事件总数,再求出田忌的马获胜包含的基本事件种数,由此能求出田忌的马获胜的概率.
【详解】分别用A,B,C表示齐王的上、中、下等马,用a,b,c表示田忌的上、中、下等马,现从双方的马匹中随机选一匹进行一场比赛有Aa,Ab,Ac,Ba,Bb,Bc,Ca,Cb,Cc共9场比赛,其中田忌马获胜的有Ba,Ca,Cb共3场比赛,所以田忌马获胜的概率为.
故选:A.
【点睛】本题考查概率的求法,考查等可能事件概率计算公式等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
8.B
【分析】计算出三种规则下甲发球和乙发球的概率,当两人发球的概率均为时,该规则对甲、乙公平,由此可得出正确选项.
【详解】对于规则一,每人发球的机率都是,是公平的;
对于规则二,记个红球分别为红,红,个黑球分别为黑、黑,
则随机取出个球的所有可能的情况有(红,红),(红,黑),(红,黑),(红,黑),(红,黑),(黑,黑),共种,其中同色的情况有种,
所以甲发球的可能性为,不公平;
对于规则三,记个红球分别为红、红、红,则随机取出个球所有可能的情况有(红,红),(红,红),(红,黑),(红,红),(红,黑),(红,黑),共种,其中同色的情况有种,所以两人发球的可能性均为,是公平的.
因此,对甲、乙公平的规则是规则一和规则三.
故选B.
【点睛】本题考查利用规则的公平性问题,同时也考查了利用古典概型的概率公式计算事件的概率,正确理解题意是解题的关键,考查计算能力,属于中等题.
9.A
【分析】计算出小正方体的个数,并数出恰有一面涂有颜色的小正方体的个数,利用古典概型概率公式即可计算出所求事件的概率.
【详解】将棱长为的正方体均匀切割成棱长为的小正方体,一共可切割成块,而只有位于大正方体的各个面中心的小正方体恰有一面涂有颜色,共块,
因此,所得小正方体恰有一面涂有颜色的概率是.
故选A.
【点睛】本题考查利用古典概型概率公式计算所求事件的概率,考查计算能力,属于基础题.
10.D
【分析】彩票中奖的概率为,只是指中奖的可能性为
【详解】彩票中奖的概率为,只是指中奖的可能性为,
不是买10000张彩票一定能中奖,
概率是指试验次数越来越大时,频率越接近概率.所以选D.
【点睛】概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,是否中奖是随机事件.
11.D
【详解】由题意,试验的情况总数有,
又,即两次所记数字之和能整除的有:
,,,两次交换顺序共8种,还有,
即所求事件个数共有,所以所求概率为.
故选:D.
12.B
【详解】试题分析:设小明本次电工考试中共参加3次考试为事件,小明本次电工考试中第一次理论考试没通过,第二次理论考试通过,第一次操作考试通过为事件,小明本次电工考试中第一次理论考试通过,第一次操作考试没通过,第二次操作考试通过为事件,则,而,,所以,故应填.
考点:1、独立事件的概率公式;
13.B
【详解】试题分析:就业形势的好坏,主要看招聘人数与应聘人数的比值,比值越大,就业形势越好,故选B.
考点:本题主要考查不等式的概念、不等式的性质.
点评:解答此类题目,首先要审清题意,明确就业形势的好坏,主要看招聘人数与应聘人数的比值.
14.B
【详解】∵用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,
∴建筑行业招聘人数是76516,而应聘人数没有排在前五位,小于65280,
建筑行业人才是供不应求,
∵物流行业应聘人数是74570,
而招聘人数不在前五位,要小于70436,
∴物流行业是供大于求,
∴就业形势是建筑行业好于物流行业,
故选B.
15.D
【分析】先逐个求解所有5个三角形的面积,再根据要求计算概率.
【详解】如图所示,,,,,的面积分别为,,.
将,,,,分别记为,,,,,从这5个三角形中任取出2个,则样本空间,共有10个样本点.
记事件表示“从5个三角形中任取出2个,这2个三角形的面积之和不小于另外3个三角形面积之和”,则事件包含的样本点为,,,共3个,所以.
故选:D.
16.甲.
【解析】分别求出甲箱中取到白球的概率和乙箱中取到白球的概率,由此进行判断.
【详解】解:甲箱有99个白球1个黑球,
随机地取出一球,得白球的可能性是,
乙箱中有1个白球和99个黑球,从中任取一球,得白球的可能性是,
由此看到,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.
既然在一次抽样中抽得白球,当然可以认为是由概率大的箱子中抽出的.
我们作出推断是从甲箱中抽出的.
故答案为:甲
【点睛】本题考查概率的应用,属于基础题,解题时要认真审题,注意概率的计算.
17.133.3.
【解析】根据分位数的定义计算可得.
【详解】解析:分数在130以下的学生所占比例为.
在140以下的学生所占比例为.
因此,80%分位数一定位于内,由.
可以估计80%分位数为133.3.
答案:133.3.
【点睛】本题考查分位数的概念,属于基础题.
18.
【分析】利用列举法求出方案一坐到“3号”车的概率为,利用古典概型求出方案二坐到“3号”车的概率为,由此能求出结果
【详解】三辆车的出车顺序可能为:123、132、213、231、312、321
方案一坐车可能:132、213、231,所以,;
方案二坐车可能:312、321,所以,;
所以,
答案:
【点睛】本题考查概率的计算,属于基础题
19..
【分析】第一局失利,最终经过5局比赛获得冠军,说明第2,3,4局胜2局,胜1局,根据相互独立事件的概率公式计算即可.
【详解】第1局失利为事实,经过5局获胜,第2,3,4局胜2局,胜1局,5局比赛最终获得冠军的概率是.
【点睛】本题主要考查了相互独立事件的概率乘法公式,属于中档题.
20.
【详解】选手甲选择A类题目,得分的均值为:
0.6×300+0.4×( 300)=60,
选手甲选择B类题目,得分的均值为:
0.75×200+0.25×( 200)=100,
选手甲选择C类题目,得分的均值为:
0.85×100+0.15×( 100)=70,
∴若要每一次答题的均分更大一些,
则选手甲应选择的题目类型应为B.
故答案为:B.
21.(1)答案见解析
(2)对甲、乙两名同学不公平,理由见解析.
【详解】(1)树状图法:画出树状图,如图所示:
从上面的树状图,知由1,2,3,4,5,6可组成20个“三位递增数”;
列举法:由题意,知由1,2,3,4,5,6组成的“三位递增数”分别是123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456,
共20个,故由1,2,3,4,5,6可组成20个“三位递增数”.
(2)不公平.理由如下:
由(1),知由1,2,3,4,5,6组成的“三位递增数”有20个记“甲参加数学竞赛”为事件,事件包含的样本点有124,126,134,136,146,156,234,236,246,256,346,356,456,共13个.
所以.
记“乙参加数学竞赛”为事件,则事件包含的样本点有123,125,135,145,235,245,345,共7个.
所以.因为,
所以该选取规则对甲、乙两名同学不公平.
22.(1)患病者的人数为40,,;(2)31450;(3).
【分析】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为40人,由此能求出,.
(2)指标检测值不低于5的样本中,有患病者28人,未患病者9人,共37人,此地区该项身体指标检测值不低于5的从业者的人数.
(3)当时,在100个样本数据中,有12名患病者被误判为未患病,有9名未患病者被误判为患病者,由此能判断错误的概率.
【详解】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为.
,.
(2)由(1)可知,患病者的人数为,未患病的人数为,该项身体指标检测值不低于5的样本中,有患病者(人),未患病者(人),共37人.
故估计此地区该项身体指标检测值不低于5的从业者的人数为.
(3)当时,在100个样本数据中,有(名)患病者被误判为未患病,有(名)未患病者被误判为患病,
因此判断错误的概率为.
23.(1);(2);(3)第组.
【分析】(1)利用样本在上的频数除以可得所求频率;
(2)设区间中的两个数据为、,区间中的三个数据为、、,列举出所有的基本事件,并确定所求事件所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率;
(3)计算出样本的平均数,可得出结论.
【详解】(1)由已知,当空气相对湿度在时,病毒死亡较快.
而样本在上的频数为,所以所求频率为;
(2)设事件为“从区间的数据中任取两个数据,恰有一个数据位于内”,
设区间中的两个数据为、,区间中的三个数据为、、,
因此,从区间的数据中任取两个数据,
包含、、、、、、、、、,共个样本点,
而事件包含、、、、、,共个样本点,所以;
(3)样本的平均数为,
故样本的平均数在第组.
24.(1)该产品需要进行技术改进;(2).
【分析】(1)、由频率分布直方图求出平均值判断与16的大小关系即可得出结论;
(2)、先根据分层抽样求得在与中所抽取的个数,运用列举法列出事件的所有情况,由古典概率公式可求得答案.
【详解】(1)∵,故该产品需要进行技术改进;
(2)组的产品的个数为,组的产品的个数,所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为,组中抽取的一个为,
则从6个中抽取2个的所有情况如下:共15种情况,
其中在中恰有2个的有共10种情况,所以所求的概率.
25.(1)条形统计图见解析;(2);(3)名.
【分析】(1)本题首先可根据题意求出样本容量、八年级志愿者被抽到的人数以及九年级志愿者被抽到的人数,然后补全条形统计图即可;
(2)可根据教师志愿者被抽到的人数所占百分比求出对应的圆心角的度数;
(3)可通过总人数以及七年级志愿者所占比例得出结果.
【详解】(1)由题意知样本容量为,
则八年级志愿者被抽到的人数为,
九年级志愿者被抽到的人数为,
补全条形统计图如下:
(2)因为教师志愿者被抽到的人数所占百分比为,
所以对应的扇形的圆心角的度数为.
(3)(名),该校七年级大约有240名志愿者.
【点睛】本题考查条形统计图以及扇形统计图的实际应用,考查如何补全条形统计图,考查条形统计图以及扇形统计图之间的关系,考查计算能力,是简单题.
26.(1),,;(2)
【分析】(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,则再利用独立事件的概率计算公式,解方程组即可得到答案.
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,利用对立事件,即计算即可.
【详解】(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,
由题设条件有即
解得,,.
即甲、乙、丙三台机床各自加工的零件是一等品的概率分别是,,;
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,则
.
故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为.
【点晴】本题主要考查独立事件的概率计算问题,涉及到对立事件的概率计算,考查学生的数学运算能力,是一道容易题.
答案第1页,共2页
答案第1页,共2页
