全册综合复习训练(2022-2023学年高中数学人教B版(2019)必修2(含解析)
文档属性
| 名称 | 全册综合复习训练(2022-2023学年高中数学人教B版(2019)必修2(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 821.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-14 09:34:47 | ||
图片预览




文档简介
全册综合复习训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知且,,当时均有,则实数的取值范围是( )
A. B.
C. D.
2.若满足不等式,则函数的值域是( )
A. B. C. D.
3.已知向量,,若,则实数m的值为( )
A.4 B. C.1 D.
4.函数是上的偶函数,且在上是增函数,若,则实数的取值范围是( )
A. B. C. D.
5.“二十四节气”是上古农耕文明的产物,表达了人与自然宇宙之间独特的时间观念,是中华民族悠久文化内涵和历史沉淀.根据多年气象统计资料,某地在节气夏至当日下雨的概率为0.45,阴天的概率为0.20,则该地在节气夏至当日为晴天的概率为( )
A.0.65 B.0.55 C.0.35 D.0.75
6.一个学校高一、高二、高三的学生人数之比为2:3:5,若用分层抽样的方法抽取容量为200的样本,则应从高三学生中抽取的人数为:
A.100 B.80 C.60 D.40
7.某学生在一门功课的22次考试中,所得分数的茎叶图所示,则此学生该门功课考试成绩的极差与中位数之和为( )
A.117 B.118
C.118.5 D.119.5
8.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
9.某工厂生产甲、乙、丙三种型号的产品,产品数量之比为3:5:7,现用分层抽样的方法抽出容量为n的样本,其中甲种产品有18件,则样本容量n=( )
A.45 B.54 C.90 D.126
10.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的电费开支占总开支的百分比为( ).
A. B. C. D.
11.f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞) B.(8,9] C.[8,9] D.(0,8)
12.从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于
A. B. C. D.
13.已知向量,,若,则实数m等于( )
A.- B.
C.-或 D.0
14.已知中,点是线段上靠近的三等分点,是线段的中点,则( )
A. B.
C. D.
15.已知点则与同方向的单位向量为
A. B. C. D.
二、填空题
16.已知,若方程有四个根且,则的取值范围是______.
17.若函数f(x)=ax+loga(x+1)在[0,1]上的最大值和最小值之和为a,则a的值为________.
18.甲乙两队正在角逐排球联赛的冠军,在刚刚结束的前三局比赛中,甲队2胜1负暂时领先,若规定先胜三局者即为本次联赛冠军,已知两队在每局比赛中获胜的概率均为,且各局比赛结果相互独立,则甲队最终成为本次排球联赛冠军的概率为________.
19.某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间内,其频率分布直方图如图所示.
(Ⅰ)直方图中的_________;
(Ⅱ)在这些购物者中,消费金额在区间内的购物者的人数为_________.
20.已知正方形ABCD的边长为1,,,,则的模等于____.
21.若,且三点共线,则=______
三、解答题
22.设函数是定义R上的奇函数.
(1)求k的值;
(2)若不等式有解,求实数a的取值范围;
(3)设,求在上的最小值,并指出取得最小值时的x的值.
23.已知函数f(x)=log2.
(1)若函数f(x)是R上的奇函数,求a的值;
(2)若函数f(x)的定义域是一切实数,求a的取值范围;
(3)若函数f(x)在区间[0,1]上的最大值与最小值的差不小于2,求实数a的取值范围.
24.为研究某植物园中某类植物的高度,随机抽取了高度在(单位:cm)的50株植物,得到其高度的频率分布直方图(如图所示).
(1)求a的值;
(2)若园内有该植物2000株,试根据直方图信息估计高度在的植物数量.
25.现有8名奥运会志愿者,其中志愿者通晓日语,通晓俄语,通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求被选中的概率;
(2)求和不全被选中的概率.
26.已知向量.
(1)若,求的值;
(2)若,求的值.
27.在△ABC中,.
(1)求△ABM与△ABC的面积之比;
(2)若N为AB中点,与交于点P,且 (x,y∈R),求x+y的值.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
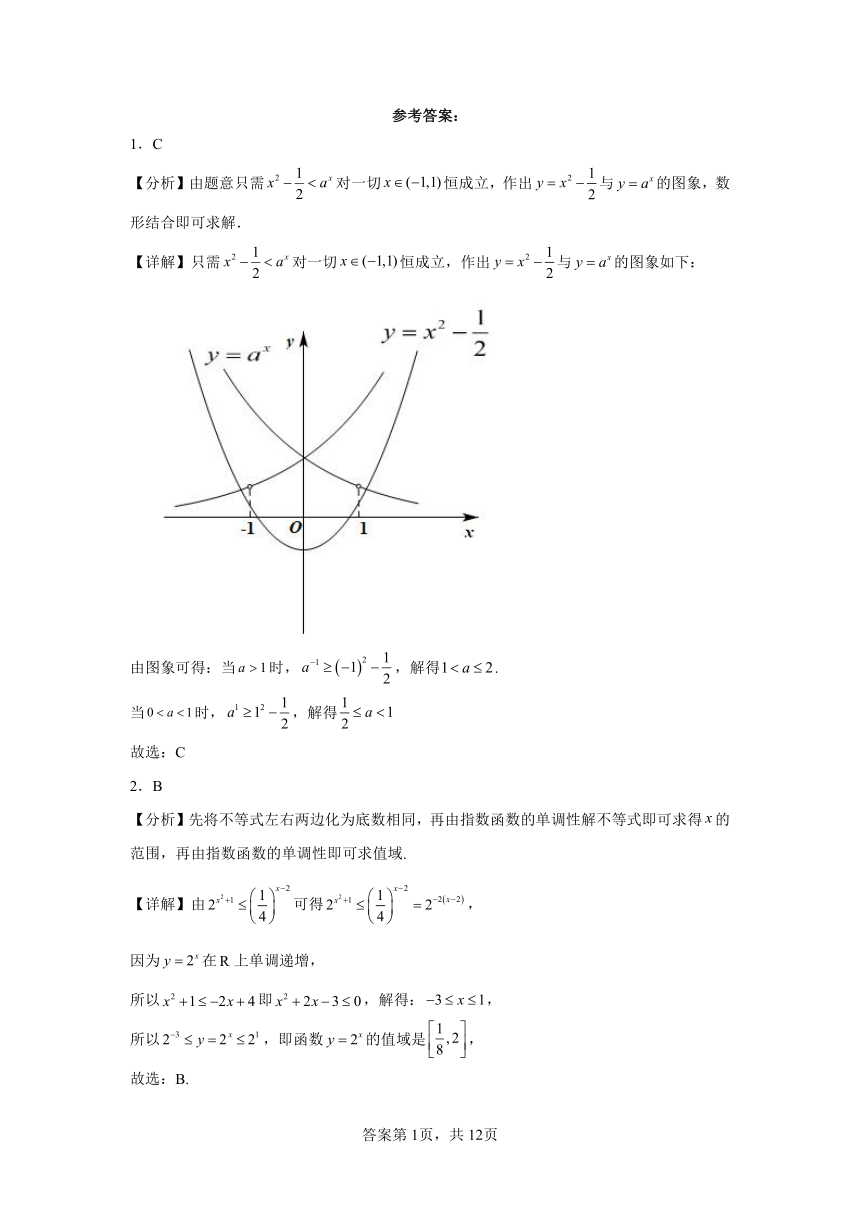
【分析】由题意只需对一切恒成立,作出与的图象,数形结合即可求解.
【详解】只需对一切恒成立,作出与的图象如下:
由图象可得:当时,,解得.
当时,,解得
故选:C
2.B
【分析】先将不等式左右两边化为底数相同,再由指数函数的单调性解不等式即可求得的范围,再由指数函数的单调性即可求值域.
【详解】由可得,
因为在上单调递增,
所以即,解得:,
所以,即函数的值域是,
故选:B.
3.B
【分析】根据向量共线的坐标运算即可得出答案.
【详解】解:因为,
所以,解得:.
故选:B.
4.D
【解析】由偶函数的性质及函数的单调性可转化条件为,即可得解.
【详解】函数是上的偶函数,且在上是增函数,
在上是减函数,
又等价于,,或,
实数的取值范围为.
故选:D.
5.C
【分析】设出三件相互互斥的事件,事件“某地在节气夏至当日下雨”为事件A,"某地在节气夏至当日阴天”为事件B,“某地在节气夏至当日晴天”为事件C,根据互斥事件概率的基本性质可得,进而可得答案.
【详解】解:设事件“某地在节气夏至当日下雨”为事件A,"某地在节气夏至当日阴天”为事件B,“某地在节气夏至当日晴天”为事件C,
由题意可得事件A,B,C为互斥事件,所以,
又,所以.
故选:C.
【点睛】本题考查求互斥事件的概率,解决此类问题的关键是熟练掌握互所事件的定义,以及概率的基本性质,属于基础题.
6.A
【分析】根据分层抽样的方法,得到高三学生抽取的人数为,即可求解,得到答案.
【详解】由题意,学校高一、高二、高三的学生人数之比为2:3:5,采用分层抽样的方法抽取容量为200的样本,所以高三学生抽取的人数为人,故选A.
【点睛】本题主要考查了分层抽样的应用,其中解答中熟记分层抽样的方法是解答的关键,着重考查了推理与运算能力,属于基础题.
7.B
【分析】根据茎叶图计算出极差和中位数,然后求和即可.
【详解】22次考试成绩最高为98分,最低为56分,所以极差为98-56=42,从小到大排列,中间两数为76,76,所以中位数为76,所以此学生该门功课考试成绩的极差与中位数之和为42+76=118,故选B.
【点睛】本题主要考查茎叶图的识别及样本数字特征求解,极差是数据最大值与最小值的差,中位数是确定数据中间位置的数,中间位置有两个数据时,取两者的平均数,侧重考查了数据分析和数学运算的核心素养.
8.A
【分析】事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
【点睛】本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
9.C
【分析】由分层抽样的特点,用A种型号产品的样本数除以A种型号产品所占的比例,即得样本的容量n.
【详解】解:A种型号产品所占的比例为,
,故样本容量n=90.
故选C.
【点睛】本题考查分层抽样的定义和方法,各层的个体数之比等于各层对应的样本数之比,属于基础题.
10.B
【分析】结合图表,通过计算可得:该学期的电费开支占总开支的百分比为 ×20%=11.25%,得解.
【详解】由图1,图2可知:该学期的电费开支占总开支的百分比为×20%=11.25%,
故选B.
【点睛】本题考查了识图能力及进行简单的合情推理,属简单题.
11.B
【分析】令x=y=3,利用f(3)=1即可求得f(9)=2,由f(x)+f(x﹣8)≤2得f[x(x﹣8)]≤f(9),再由单调性得到不等式组,解之即可.
【详解】∵f(3)=1,
∴f(9)=f(3×3)=f(3)+f(3)=2;
∵函数f(x)是定义在(0,+∞)上的增函数,
f(xy)=f(x)+f(y),f(9)=2,
∴f(x)+f(x﹣8)≤2 f[x(x﹣8)]≤f(9),
∴,
解得:8<x≤9.
∴原不等式的解集为:(8,9].
故选B.
【点睛】本题考查抽象函数及其应用,着重考查赋值法与函数单调性的应用,考查解不等式组的能力,属于中档题.
12.D
【详解】考点:古典概型及其概率计算公式.
分析:从正六边形的6个顶点中随机选择4个顶点,选择方法有C64=15种,且每种情况出现的可能性相同,故为古典概型,由列举法计算出它们作为顶点的四边形是矩形的方法种数,求比值即可.
解:从正六边形的6个顶点中随机选择4个顶点,选择方法有C64=15种,
它们作为顶点的四边形是矩形的方法种数为3,由古典概型可知
它们作为顶点的四边形是矩形的概率等于=
故选D.
13.C
【分析】应用向量平行的坐标表示列方程求参数值即可.
【详解】由知:1×2-m2=0,即或.
故选:C.
14.C
【解析】不妨设为等腰直角三角形,其中,以线段所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,分别求得向量 的坐标,利用平面向量的基本定理求解.
【详解】不妨设为等腰直角三角形,其中,以线段所在直线为轴,线段的垂直平分线为轴,建立如图所示的平面直角坐标系;
设,故,,
故,,,
故,,
设,
则,
解得,
故.
故选:C
15.A
【详解】试题分析:,所以与同方向的单位向量为,故选A.
考点:向量运算及相关概念.
16.
【分析】作出函数的图象,结合图象得出,,得到,结合指数函数的性质,即可求解.
【详解】由题意,作出函数的图象,如图所示,
因为方程有四个根且,
由图象可知,,可得,
则,
设,所以,
因为,所以,所以,
所以,即,
即的取值范围是.
故答案为:.
【点睛】本题主要考查了函数与方程的综合应用,其中解答中作出函数的图象,结合图象和指数函数的性质求解是解答的关键,着重考查数形结合思想,以及推理与运算能力.
17.
【分析】无论a取何值,函数f(x)=ax+loga(x+1)都具有单调性,因而将x=1和x=0可得到最大与最小值,代入即可求解.
【详解】函数f(x)=ax+loga(x+1) 在[0,1]上有单调性
将x=1和x=0代入可得最大值与最小值
所以
解得
【点睛】本题考查了对数单调性的简单应用,属于基础题.
18.
【解析】甲队胜包含两种情况,第四场胜;或第四场负,第五场胜,分别求出概率相加,即可求解
【详解】甲得冠军则有:甲第四场胜,概率为;
或第四场负,第五场胜,概率为,
甲队最终成为本次排球联赛冠军的概率为.
故答案为:.
【点睛】本题考查互斥事件与相互独立同时发生的概率,属于基础题.
19.(Ⅰ)3;(Ⅱ)6000.
【详解】由频率分布直方图及频率和等于1可得,
解之得.于是消费金额在区间内频率为,所以消费金额在区间内的购物者的人数为:,故应填3;6000.
考点:本题考查频率分布直方图,属基础题.
20.
【解析】由向量加法法则可求出,从而可求出模.
【详解】解:.
故答案为: .
21.10
【分析】先由三点坐标,写出向量与的坐标,再由向量共线即可得出结果.
【详解】因为,所以,,
又三点共线,所以与共线,
因此,解得.
故答案为10
【点睛】本题主要考查向量的坐标运算,熟记共线向量定理和坐标运算即可,属于基础题型.
22.(1)1;(2);(3)最小值为,此时.
【解析】(1)根据题意可得,即可求得k值,经检验,符合题意;
(2)有解,等价为,利用二次函数图象与性质,即可求得答案;
(3)由题意,令,可得t的范围,整理可得,,利用二次函数的性质,即可求得答案.
【详解】(1)因为是定义域为R上的奇函数,
所以,所以,解得,
所以,
当时,,
所以为奇函数,故;
(2)有解,所以有解,
所以只需,
因为(时,等号成立),
所以;
(3)因为,所以,
可令,可得函数t在递增,即,
则,可得函数,,
由为开口向上,对称轴为的抛物线,
所以时,取得最小值,
此时,解得,
所以在上的最小值为,此时.
【点睛】解题的关键熟练掌握二次函数的图象与性质,并灵活应用,处理存在性问题时,若,只需,若,只需,处理恒成立问题时,若,只需,若,只需,考查分析理解,计算化简的能力属中档题.
23.(1)a=0;(2)a≥0;(3)-【分析】(1)由解得,然后检验函数是奇函数即可;
(2)由真数恒大于0即恒成立可得;
(3)由函数单调性得,解之可得.
【详解】(1)若函数f(x)是R上的奇函数,
则f(0)=0,解得a=0.
当a=0时,f(x)=-x=-f(-x)是R上的奇函数,
所以a=0为所求.
(2)若函数f(x)的定义域是一切实数,则+a>0恒成立,即a>-恒成立,由于-∈(-∞,0),
故只要a≥0即可.
(3)由已知,得函数f(x)是减函数,故f(x)在区间[0,1]上的最大值是f(0)=log2(1+a),
最小值是f(1)=log2.
由题设,得log2(1+a)-log2≥2 ,解得-【点睛】本题考查对数函数的性质,掌握对数型复合函数的奇偶性、单调性的研究方法是解题关键.
24.(1);
(2)560.
【分析】(1)根据直方图中频率之和为1列出方程求解a即可;
(2)由直方图可得出株高落在范围内的频率,根据频率计算频数即可.
(1)
根据频率分布直方图可知,,
解得;
(2)
因为高度落在的植物的频率为,
所以高度在的植物数量为株.
25.(1);(2).
【详解】(1)从8人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间
{,,
,,,
,,,
}
由18个基本事件组成.由于每一个基本事件被抽取的机会均等,
因此这些基本事件的发生是等可能的.用表示“恰被选中”这一事件,则
{,
}
事件由6个基本事件组成,因而.
(2)用表示“不全被选中”这一事件,则其对立事件表示“全被选中”这一事件,
由于{},事件有3个基本事件组成,
所以,由对立事件的概率公式得.
26.(1);(2)或.
【分析】(1)利用向量平行的坐标表示列方程,解方程求得的值.
(2)利用向量模的坐标运算列方程,解方程求得的值.
【详解】(1),由于,所以,即.
(2),依题意,所以,解得或.
【点睛】本小题主要考查向量线性运算的坐标表示,考查向量平行的坐标表示,考查向量模的坐标表示,属于中档题.
27.(1) ; (2) .
【分析】(1)由 ,即点M在线段BC上的靠近B的四等分点即可,
(2)由题可得 由 (x,y∈R),所以x=3y,
因为N为AB的中点,可得,由此可得 ,即可求得x+y的值.
【详解】(1)在△ABC中,=+,
4=3+,3(-)=-,
即3=,即点M是线段BC靠近B点的四等分点.
故△ABM与△ABC的面积之比为.
(2)因为=+,∥,
=x+y (x,y∈R),所以x=3y,
因为N为AB的中点,
所以=-=x+y-
=+y,
=-=x+y-
=x+(y-1),
因为∥,所以 (y-1)=xy,
即2x+y=1,又x=3y,
所以x=,y=,所以x+y=.
【点睛】本题考查了向量的线性运算,属于基础题.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知且,,当时均有,则实数的取值范围是( )
A. B.
C. D.
2.若满足不等式,则函数的值域是( )
A. B. C. D.
3.已知向量,,若,则实数m的值为( )
A.4 B. C.1 D.
4.函数是上的偶函数,且在上是增函数,若,则实数的取值范围是( )
A. B. C. D.
5.“二十四节气”是上古农耕文明的产物,表达了人与自然宇宙之间独特的时间观念,是中华民族悠久文化内涵和历史沉淀.根据多年气象统计资料,某地在节气夏至当日下雨的概率为0.45,阴天的概率为0.20,则该地在节气夏至当日为晴天的概率为( )
A.0.65 B.0.55 C.0.35 D.0.75
6.一个学校高一、高二、高三的学生人数之比为2:3:5,若用分层抽样的方法抽取容量为200的样本,则应从高三学生中抽取的人数为:
A.100 B.80 C.60 D.40
7.某学生在一门功课的22次考试中,所得分数的茎叶图所示,则此学生该门功课考试成绩的极差与中位数之和为( )
A.117 B.118
C.118.5 D.119.5
8.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
9.某工厂生产甲、乙、丙三种型号的产品,产品数量之比为3:5:7,现用分层抽样的方法抽出容量为n的样本,其中甲种产品有18件,则样本容量n=( )
A.45 B.54 C.90 D.126
10.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的电费开支占总开支的百分比为( ).
A. B. C. D.
11.f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞) B.(8,9] C.[8,9] D.(0,8)
12.从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于
A. B. C. D.
13.已知向量,,若,则实数m等于( )
A.- B.
C.-或 D.0
14.已知中,点是线段上靠近的三等分点,是线段的中点,则( )
A. B.
C. D.
15.已知点则与同方向的单位向量为
A. B. C. D.
二、填空题
16.已知,若方程有四个根且,则的取值范围是______.
17.若函数f(x)=ax+loga(x+1)在[0,1]上的最大值和最小值之和为a,则a的值为________.
18.甲乙两队正在角逐排球联赛的冠军,在刚刚结束的前三局比赛中,甲队2胜1负暂时领先,若规定先胜三局者即为本次联赛冠军,已知两队在每局比赛中获胜的概率均为,且各局比赛结果相互独立,则甲队最终成为本次排球联赛冠军的概率为________.
19.某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间内,其频率分布直方图如图所示.
(Ⅰ)直方图中的_________;
(Ⅱ)在这些购物者中,消费金额在区间内的购物者的人数为_________.
20.已知正方形ABCD的边长为1,,,,则的模等于____.
21.若,且三点共线,则=______
三、解答题
22.设函数是定义R上的奇函数.
(1)求k的值;
(2)若不等式有解,求实数a的取值范围;
(3)设,求在上的最小值,并指出取得最小值时的x的值.
23.已知函数f(x)=log2.
(1)若函数f(x)是R上的奇函数,求a的值;
(2)若函数f(x)的定义域是一切实数,求a的取值范围;
(3)若函数f(x)在区间[0,1]上的最大值与最小值的差不小于2,求实数a的取值范围.
24.为研究某植物园中某类植物的高度,随机抽取了高度在(单位:cm)的50株植物,得到其高度的频率分布直方图(如图所示).
(1)求a的值;
(2)若园内有该植物2000株,试根据直方图信息估计高度在的植物数量.
25.现有8名奥运会志愿者,其中志愿者通晓日语,通晓俄语,通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求被选中的概率;
(2)求和不全被选中的概率.
26.已知向量.
(1)若,求的值;
(2)若,求的值.
27.在△ABC中,.
(1)求△ABM与△ABC的面积之比;
(2)若N为AB中点,与交于点P,且 (x,y∈R),求x+y的值.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
【分析】由题意只需对一切恒成立,作出与的图象,数形结合即可求解.
【详解】只需对一切恒成立,作出与的图象如下:
由图象可得:当时,,解得.
当时,,解得
故选:C
2.B
【分析】先将不等式左右两边化为底数相同,再由指数函数的单调性解不等式即可求得的范围,再由指数函数的单调性即可求值域.
【详解】由可得,
因为在上单调递增,
所以即,解得:,
所以,即函数的值域是,
故选:B.
3.B
【分析】根据向量共线的坐标运算即可得出答案.
【详解】解:因为,
所以,解得:.
故选:B.
4.D
【解析】由偶函数的性质及函数的单调性可转化条件为,即可得解.
【详解】函数是上的偶函数,且在上是增函数,
在上是减函数,
又等价于,,或,
实数的取值范围为.
故选:D.
5.C
【分析】设出三件相互互斥的事件,事件“某地在节气夏至当日下雨”为事件A,"某地在节气夏至当日阴天”为事件B,“某地在节气夏至当日晴天”为事件C,根据互斥事件概率的基本性质可得,进而可得答案.
【详解】解:设事件“某地在节气夏至当日下雨”为事件A,"某地在节气夏至当日阴天”为事件B,“某地在节气夏至当日晴天”为事件C,
由题意可得事件A,B,C为互斥事件,所以,
又,所以.
故选:C.
【点睛】本题考查求互斥事件的概率,解决此类问题的关键是熟练掌握互所事件的定义,以及概率的基本性质,属于基础题.
6.A
【分析】根据分层抽样的方法,得到高三学生抽取的人数为,即可求解,得到答案.
【详解】由题意,学校高一、高二、高三的学生人数之比为2:3:5,采用分层抽样的方法抽取容量为200的样本,所以高三学生抽取的人数为人,故选A.
【点睛】本题主要考查了分层抽样的应用,其中解答中熟记分层抽样的方法是解答的关键,着重考查了推理与运算能力,属于基础题.
7.B
【分析】根据茎叶图计算出极差和中位数,然后求和即可.
【详解】22次考试成绩最高为98分,最低为56分,所以极差为98-56=42,从小到大排列,中间两数为76,76,所以中位数为76,所以此学生该门功课考试成绩的极差与中位数之和为42+76=118,故选B.
【点睛】本题主要考查茎叶图的识别及样本数字特征求解,极差是数据最大值与最小值的差,中位数是确定数据中间位置的数,中间位置有两个数据时,取两者的平均数,侧重考查了数据分析和数学运算的核心素养.
8.A
【分析】事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
【点睛】本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
9.C
【分析】由分层抽样的特点,用A种型号产品的样本数除以A种型号产品所占的比例,即得样本的容量n.
【详解】解:A种型号产品所占的比例为,
,故样本容量n=90.
故选C.
【点睛】本题考查分层抽样的定义和方法,各层的个体数之比等于各层对应的样本数之比,属于基础题.
10.B
【分析】结合图表,通过计算可得:该学期的电费开支占总开支的百分比为 ×20%=11.25%,得解.
【详解】由图1,图2可知:该学期的电费开支占总开支的百分比为×20%=11.25%,
故选B.
【点睛】本题考查了识图能力及进行简单的合情推理,属简单题.
11.B
【分析】令x=y=3,利用f(3)=1即可求得f(9)=2,由f(x)+f(x﹣8)≤2得f[x(x﹣8)]≤f(9),再由单调性得到不等式组,解之即可.
【详解】∵f(3)=1,
∴f(9)=f(3×3)=f(3)+f(3)=2;
∵函数f(x)是定义在(0,+∞)上的增函数,
f(xy)=f(x)+f(y),f(9)=2,
∴f(x)+f(x﹣8)≤2 f[x(x﹣8)]≤f(9),
∴,
解得:8<x≤9.
∴原不等式的解集为:(8,9].
故选B.
【点睛】本题考查抽象函数及其应用,着重考查赋值法与函数单调性的应用,考查解不等式组的能力,属于中档题.
12.D
【详解】考点:古典概型及其概率计算公式.
分析:从正六边形的6个顶点中随机选择4个顶点,选择方法有C64=15种,且每种情况出现的可能性相同,故为古典概型,由列举法计算出它们作为顶点的四边形是矩形的方法种数,求比值即可.
解:从正六边形的6个顶点中随机选择4个顶点,选择方法有C64=15种,
它们作为顶点的四边形是矩形的方法种数为3,由古典概型可知
它们作为顶点的四边形是矩形的概率等于=
故选D.
13.C
【分析】应用向量平行的坐标表示列方程求参数值即可.
【详解】由知:1×2-m2=0,即或.
故选:C.
14.C
【解析】不妨设为等腰直角三角形,其中,以线段所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,分别求得向量 的坐标,利用平面向量的基本定理求解.
【详解】不妨设为等腰直角三角形,其中,以线段所在直线为轴,线段的垂直平分线为轴,建立如图所示的平面直角坐标系;
设,故,,
故,,,
故,,
设,
则,
解得,
故.
故选:C
15.A
【详解】试题分析:,所以与同方向的单位向量为,故选A.
考点:向量运算及相关概念.
16.
【分析】作出函数的图象,结合图象得出,,得到,结合指数函数的性质,即可求解.
【详解】由题意,作出函数的图象,如图所示,
因为方程有四个根且,
由图象可知,,可得,
则,
设,所以,
因为,所以,所以,
所以,即,
即的取值范围是.
故答案为:.
【点睛】本题主要考查了函数与方程的综合应用,其中解答中作出函数的图象,结合图象和指数函数的性质求解是解答的关键,着重考查数形结合思想,以及推理与运算能力.
17.
【分析】无论a取何值,函数f(x)=ax+loga(x+1)都具有单调性,因而将x=1和x=0可得到最大与最小值,代入即可求解.
【详解】函数f(x)=ax+loga(x+1) 在[0,1]上有单调性
将x=1和x=0代入可得最大值与最小值
所以
解得
【点睛】本题考查了对数单调性的简单应用,属于基础题.
18.
【解析】甲队胜包含两种情况,第四场胜;或第四场负,第五场胜,分别求出概率相加,即可求解
【详解】甲得冠军则有:甲第四场胜,概率为;
或第四场负,第五场胜,概率为,
甲队最终成为本次排球联赛冠军的概率为.
故答案为:.
【点睛】本题考查互斥事件与相互独立同时发生的概率,属于基础题.
19.(Ⅰ)3;(Ⅱ)6000.
【详解】由频率分布直方图及频率和等于1可得,
解之得.于是消费金额在区间内频率为,所以消费金额在区间内的购物者的人数为:,故应填3;6000.
考点:本题考查频率分布直方图,属基础题.
20.
【解析】由向量加法法则可求出,从而可求出模.
【详解】解:.
故答案为: .
21.10
【分析】先由三点坐标,写出向量与的坐标,再由向量共线即可得出结果.
【详解】因为,所以,,
又三点共线,所以与共线,
因此,解得.
故答案为10
【点睛】本题主要考查向量的坐标运算,熟记共线向量定理和坐标运算即可,属于基础题型.
22.(1)1;(2);(3)最小值为,此时.
【解析】(1)根据题意可得,即可求得k值,经检验,符合题意;
(2)有解,等价为,利用二次函数图象与性质,即可求得答案;
(3)由题意,令,可得t的范围,整理可得,,利用二次函数的性质,即可求得答案.
【详解】(1)因为是定义域为R上的奇函数,
所以,所以,解得,
所以,
当时,,
所以为奇函数,故;
(2)有解,所以有解,
所以只需,
因为(时,等号成立),
所以;
(3)因为,所以,
可令,可得函数t在递增,即,
则,可得函数,,
由为开口向上,对称轴为的抛物线,
所以时,取得最小值,
此时,解得,
所以在上的最小值为,此时.
【点睛】解题的关键熟练掌握二次函数的图象与性质,并灵活应用,处理存在性问题时,若,只需,若,只需,处理恒成立问题时,若,只需,若,只需,考查分析理解,计算化简的能力属中档题.
23.(1)a=0;(2)a≥0;(3)-
(2)由真数恒大于0即恒成立可得;
(3)由函数单调性得,解之可得.
【详解】(1)若函数f(x)是R上的奇函数,
则f(0)=0,解得a=0.
当a=0时,f(x)=-x=-f(-x)是R上的奇函数,
所以a=0为所求.
(2)若函数f(x)的定义域是一切实数,则+a>0恒成立,即a>-恒成立,由于-∈(-∞,0),
故只要a≥0即可.
(3)由已知,得函数f(x)是减函数,故f(x)在区间[0,1]上的最大值是f(0)=log2(1+a),
最小值是f(1)=log2.
由题设,得log2(1+a)-log2≥2 ,解得-
24.(1);
(2)560.
【分析】(1)根据直方图中频率之和为1列出方程求解a即可;
(2)由直方图可得出株高落在范围内的频率,根据频率计算频数即可.
(1)
根据频率分布直方图可知,,
解得;
(2)
因为高度落在的植物的频率为,
所以高度在的植物数量为株.
25.(1);(2).
【详解】(1)从8人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间
{,,
,,,
,,,
}
由18个基本事件组成.由于每一个基本事件被抽取的机会均等,
因此这些基本事件的发生是等可能的.用表示“恰被选中”这一事件,则
{,
}
事件由6个基本事件组成,因而.
(2)用表示“不全被选中”这一事件,则其对立事件表示“全被选中”这一事件,
由于{},事件有3个基本事件组成,
所以,由对立事件的概率公式得.
26.(1);(2)或.
【分析】(1)利用向量平行的坐标表示列方程,解方程求得的值.
(2)利用向量模的坐标运算列方程,解方程求得的值.
【详解】(1),由于,所以,即.
(2),依题意,所以,解得或.
【点睛】本小题主要考查向量线性运算的坐标表示,考查向量平行的坐标表示,考查向量模的坐标表示,属于中档题.
27.(1) ; (2) .
【分析】(1)由 ,即点M在线段BC上的靠近B的四等分点即可,
(2)由题可得 由 (x,y∈R),所以x=3y,
因为N为AB的中点,可得,由此可得 ,即可求得x+y的值.
【详解】(1)在△ABC中,=+,
4=3+,3(-)=-,
即3=,即点M是线段BC靠近B点的四等分点.
故△ABM与△ABC的面积之比为.
(2)因为=+,∥,
=x+y (x,y∈R),所以x=3y,
因为N为AB的中点,
所以=-=x+y-
=+y,
=-=x+y-
=x+(y-1),
因为∥,所以 (y-1)=xy,
即2x+y=1,又x=3y,
所以x=,y=,所以x+y=.
【点睛】本题考查了向量的线性运算,属于基础题.
答案第1页,共2页
答案第1页,共2页
