19.2.3 一次函数与方程、不等式 课件 (共18张PPT)
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式 课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 07:21:54 | ||
图片预览





文档简介
第十九章 一次函数
19.2.3一次函数与方程、不等式
理解一次函数与一元-次方程的关系;一次函数与一元一次不等式的关系理解一次函数与二元一次方程(组)的对应关系;
核心素养目标:
会用函数的方法求解一元一次方程.会根据一次函数图像解决一元一次不等式的问题.会用画图象的方法解二元一次方程组;
通过教学活动,让学生学会从不同角度认识事物本质的方法,建立自信心,提高学生自主合作探究学习的意识和能力,激发学生学习的兴趣,让学生体验数学的价值
今天数学王国搞了个家庭Party,各个成员按照自己所在的集合就坐,这时来了“x+y=5”.
二元一次方程
一次函数
x+y=5
到我这里来
到我这里来
这是怎么回事? x+y=5应该坐在哪里呢?
情境引入:
3
2
1
2
1
-2
O
x
y
-1
-1
3
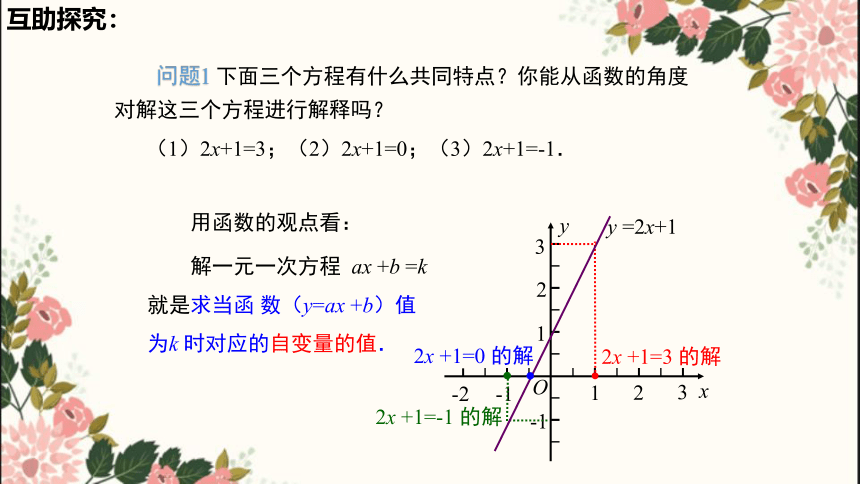
问题1 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程 ax +b =k 就是求当函 数(y=ax +b)值为k 时对应的自变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
互助探究:
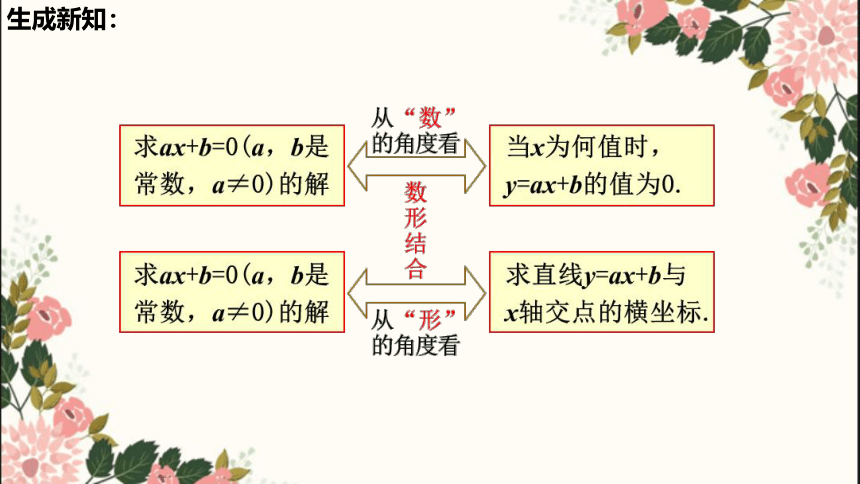
生成新知:
1.直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
-10
0
-10
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(____,_____).
5
0
跟踪练习:
跟踪练习:
1.已知一次函数y=-2x+2,根据图象回答:
(1)当y=0时,求x的值;
(2)当y=2时,求x的值.
解:(1)由图象可知:一次函数y=-2x+2与x轴的交点为(1,0)∴ 当y=0时,x=1(2)由图象可知:一次函数y=-2x+2与y轴的交点为(0,2)∴ 当y=2时,x=0
跟踪练习:
2.利用一次函数图象解方程5x-1=2x+5.
解:原方程变形为3x-6=0,并画出一次函数y=3x-6的图象.由图象可知一次函数y=3x-6与x轴交点为(2,0)因此,方程3x-6=0的解为x=2,即方程5x-1=2x+5的解为x=2.
问题2 下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
不等式ax+b>c的解集就是
使函数y =ax+b 的函数值大于c
的对应的自变量取值范围;
不等式ax+b<c的解集就是
使函数y =ax+b 的函数值小于c
的对应的自变量取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
y =0
y =-1
互助探究:
生成新知:
例1 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
例题精讲:
跟踪练习:
1.当自变量x的取值满足什么条件时,函数y=-5x+8的值满足下列条件?
(1) y>0;________ (2) y≤-2. ________
2.利用函数图象解不等式:6x-4≤3x+2.
解:原不等式变形为3x-6≤0
画出函数y=3x-6的图像
由图像可以看出:当x≤2时,
这条直线上的点在x轴的下方,
这时y=3x-6≤0
即原不等式的解集为:x≤2.
问题3 1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
互助探究:
生成新知:
O
y
x
例2 如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求直线l1与l2的解析式,进而通过方程组求出交点坐标.
解方程组
y =2x+2
y =-x+3
解:因为直线l1过点(-1,0),
(0,2) ,用待定系数法可求得
直线l1的解析式为y =2x+2.同理
可求得直线l2的解析式为y =-x+3.
得
x=
y=
即直线l1与l2 的交点坐标
为
例题精讲:
跟踪练习:
考虑下表两种移动电话计费方式
用函数方法解答何时两种计费方式费用相等.
一次函数与方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
解二元一次方程组 求对应两条直线交点的坐标 .
课堂小结:
课后作业:
必做题:教材习题19.2第8、10题.
选做题:教材习题19.2第11、13题.
19.2.3一次函数与方程、不等式
理解一次函数与一元-次方程的关系;一次函数与一元一次不等式的关系理解一次函数与二元一次方程(组)的对应关系;
核心素养目标:
会用函数的方法求解一元一次方程.会根据一次函数图像解决一元一次不等式的问题.会用画图象的方法解二元一次方程组;
通过教学活动,让学生学会从不同角度认识事物本质的方法,建立自信心,提高学生自主合作探究学习的意识和能力,激发学生学习的兴趣,让学生体验数学的价值
今天数学王国搞了个家庭Party,各个成员按照自己所在的集合就坐,这时来了“x+y=5”.
二元一次方程
一次函数
x+y=5
到我这里来
到我这里来
这是怎么回事? x+y=5应该坐在哪里呢?
情境引入:
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题1 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程 ax +b =k 就是求当函 数(y=ax +b)值为k 时对应的自变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
互助探究:
生成新知:
1.直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
-10
0
-10
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(____,_____).
5
0
跟踪练习:
跟踪练习:
1.已知一次函数y=-2x+2,根据图象回答:
(1)当y=0时,求x的值;
(2)当y=2时,求x的值.
解:(1)由图象可知:一次函数y=-2x+2与x轴的交点为(1,0)∴ 当y=0时,x=1(2)由图象可知:一次函数y=-2x+2与y轴的交点为(0,2)∴ 当y=2时,x=0
跟踪练习:
2.利用一次函数图象解方程5x-1=2x+5.
解:原方程变形为3x-6=0,并画出一次函数y=3x-6的图象.由图象可知一次函数y=3x-6与x轴交点为(2,0)因此,方程3x-6=0的解为x=2,即方程5x-1=2x+5的解为x=2.
问题2 下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?能把你得到的
结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
不等式ax+b>c的解集就是
使函数y =ax+b 的函数值大于c
的对应的自变量取值范围;
不等式ax+b<c的解集就是
使函数y =ax+b 的函数值小于c
的对应的自变量取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
y =0
y =-1
互助探究:
生成新知:
例1 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
例题精讲:
跟踪练习:
1.当自变量x的取值满足什么条件时,函数y=-5x+8的值满足下列条件?
(1) y>0;________ (2) y≤-2. ________
2.利用函数图象解不等式:6x-4≤3x+2.
解:原不等式变形为3x-6≤0
画出函数y=3x-6的图像
由图像可以看出:当x≤2时,
这条直线上的点在x轴的下方,
这时y=3x-6≤0
即原不等式的解集为:x≤2.
问题3 1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
互助探究:
生成新知:
O
y
x
例2 如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求直线l1与l2的解析式,进而通过方程组求出交点坐标.
解方程组
y =2x+2
y =-x+3
解:因为直线l1过点(-1,0),
(0,2) ,用待定系数法可求得
直线l1的解析式为y =2x+2.同理
可求得直线l2的解析式为y =-x+3.
得
x=
y=
即直线l1与l2 的交点坐标
为
例题精讲:
跟踪练习:
考虑下表两种移动电话计费方式
用函数方法解答何时两种计费方式费用相等.
一次函数与方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
解二元一次方程组 求对应两条直线交点的坐标 .
课堂小结:
课后作业:
必做题:教材习题19.2第8、10题.
选做题:教材习题19.2第11、13题.
