19.2.2 一次函数性质课件
文档属性
| 名称 | 19.2.2 一次函数性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-25 09:32:30 | ||
图片预览







文档简介
课件25张PPT。19.2.2 一次函数的性质人教版·八年级轻松快乐学数学1、掌握一次函数y=kx+b的性质。 2、利用一次函数y=kx+b的图象与性质解决有关问题。之学习目标1、说出一次函数y=2x+3与y=2x的关系。 ①从解析式来看 ②从图像来看 2、一次函数y=kx+b中的常量b决定了其图像与___轴的交点,其坐标为_____。之我来抢答问:一次函数y=kx+b的图象是一条直线,它与坐标轴的交点坐标是什么? 由此我们可以知道直线y=kx+b与y轴交于(0,b)点与x轴交于(-b/k,0)之合作互助1)、当x=0时,你能求出y的值吗?你能由此确定函数图象过哪个点吗?你知道这个点的位置吗?2)、当y=0时,你能求出x的值吗?你能由此确定函数图象过哪个点吗?你知道这个点的位置吗?之轻松过关
在同一直角坐标系中分别作出下列一次函数的图象
y=-2x-6 y=3x-3
y=0.5x+1 y=-x-2借助工具可以更快更准确的画出函数图像。之看谁画的好一次函数y=kx+b有下列性质:
1.当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
2.当k<0时,y随x的增大而___,这时函数的图象从左到右___.
3. 当b>0,直线与y轴交于正半轴;当b<0时,直线与y轴交于负半轴.
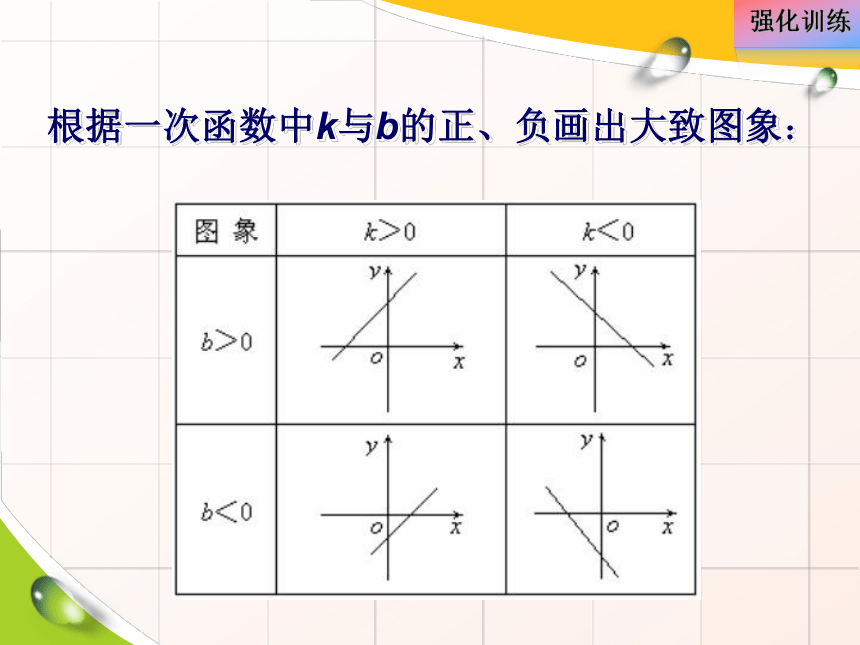
4. 一次函数y=kx+b与y轴的交点是____,与x轴的交点是_____.之规律我来找 根据一次函数中k与b的正、负画出大致图象:
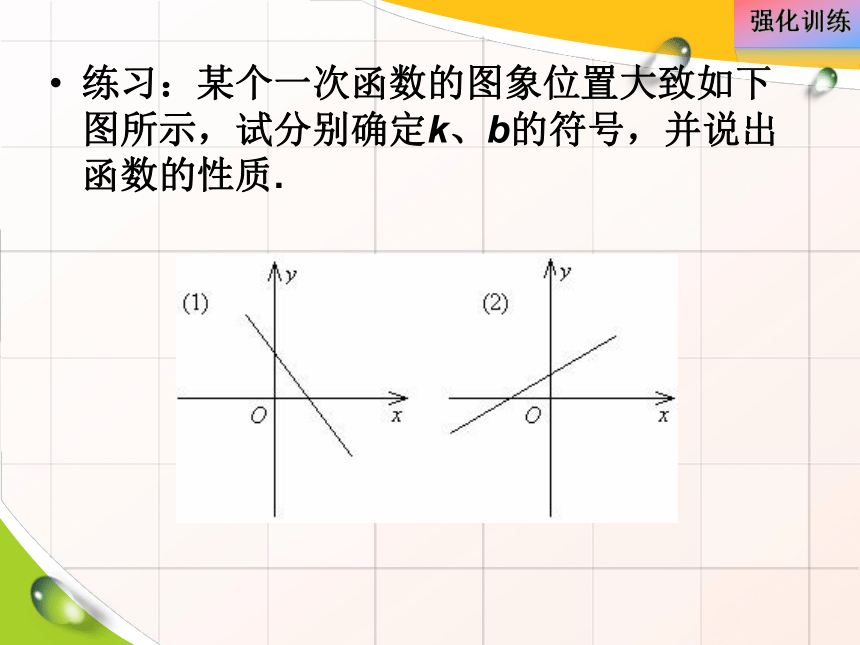
练习:某个一次函数的图象位置大致如下图所示,试分别确定k、b的符号,并说出函数的性质. 如果没有给出解析式,而是填写了其中一格,
你能填好其它格子吗?之让我考考你例 对于一次函数y=(a+4)x+2a-1,如果y随x的增大而增大,且它的图象与y轴的交点在x轴的下方,试求a的取值范围。解:因为y随x的增大而增大,
所以 a+4>0 即 a>-4又因为它的图象与y轴的交点在x轴的下方
所以 2a-1 < 0 即 a < 1/2所以 -4 < a < 1/2之例题我来讲 已知点(2,m) 、(-1,n)都在直线y=2x+3 上,试比较 m和n的大小。解:把两点的坐标代入函数关系式
当 x=2 时, m=7 , 当 x= -1 时, n=1
所以 m > n方法二 因为 k=2 >0,所以函数y随x增加而
增加 。从而直接得到 m > n之挑战不畏难 画出函数y=-2x+2的图象,结合图象回答下列问题:
(1)?? 这个函数中,随着x的增大,y将增大还是减小?
它的图象从左到右怎样变化?
(2)?? 当x取何值时,y=0? 当x取何值时,y>0?
当0减小,函数图象从左到右下降。(2)因为 y=0 所以 -2x+2=0 ,x=1因为 当 x=0 时 y=2 , 当 x=1 时 y=0;
又因为y随x增大而减小,所以 2 > y> 0即 0 < y<2因为 y>0 所以 -2x+2 > 0 , x < 1之拓展提高3、函数y=(m – 1)x+1是一次函数,且y随自变量x增大而减小,那么m的取值__________ m<12、函数y=2-3x,y随x的增大而______ .减小1、一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为( )C之体验成功
5、已知一次函数y=(1-2k)x+k的函数值y随x的增大而增大,且图象经过一、二、三象限,则k的取值范围是__________.6、若直线y=kx+b平行直线y=3x+2且在y轴上的的交点坐标为 (0, 5) 则k= ,b= 。354、已知一次函数y=2x+4的图象上有两点
A(3,a),B(4,b),则a与b的大小关系为_______a必做:配套练习册104页 9、10、11
选做:104页12谢谢大家拓展与应用1、一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为( )C例 题例1、已知函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
这时它的图象经过哪些象限?
(2)当 m取何值时,y随x的增大而减小?
这时它的图象经过哪些象限?解:当m+1>0即m>-1时y随x的增大而增大,当m+1<0即m<-1时y随x的增大而减小,这时它的图象经过一、三、四象限
这时它的图象经过二、三、四象限
AB1、掌握一次函数y=kx+b的性质。 2、利用一次函数y=kx+b的图象与性质解决有关问题。之我要学什么
在同一直角坐标系中分别作出下列一次函数的图象
y=-2x-6 y=3x-3
y=0.5x+1 y=-x-2借助工具可以更快更准确的画出函数图像。之看谁画的好一次函数y=kx+b有下列性质:
1.当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
2.当k<0时,y随x的增大而___,这时函数的图象从左到右___.
3. 当b>0,直线与y轴交于正半轴;当b<0时,直线与y轴交于负半轴.
4. 一次函数y=kx+b与y轴的交点是____,与x轴的交点是_____.之规律我来找 根据一次函数中k与b的正、负画出大致图象:
练习:某个一次函数的图象位置大致如下图所示,试分别确定k、b的符号,并说出函数的性质. 如果没有给出解析式,而是填写了其中一格,
你能填好其它格子吗?之让我考考你例 对于一次函数y=(a+4)x+2a-1,如果y随x的增大而增大,且它的图象与y轴的交点在x轴的下方,试求a的取值范围。解:因为y随x的增大而增大,
所以 a+4>0 即 a>-4又因为它的图象与y轴的交点在x轴的下方
所以 2a-1 < 0 即 a < 1/2所以 -4 < a < 1/2之例题我来讲 已知点(2,m) 、(-1,n)都在直线y=2x+3 上,试比较 m和n的大小。解:把两点的坐标代入函数关系式
当 x=2 时, m=7 , 当 x= -1 时, n=1
所以 m > n方法二 因为 k=2 >0,所以函数y随x增加而
增加 。从而直接得到 m > n之挑战不畏难 画出函数y=-2x+2的图象,结合图象回答下列问题:
(1)?? 这个函数中,随着x的增大,y将增大还是减小?
它的图象从左到右怎样变化?
(2)?? 当x取何值时,y=0? 当x取何值时,y>0?
当0
又因为y随x增大而减小,所以 2 > y> 0即 0 < y<2因为 y>0 所以 -2x+2 > 0 , x < 1之拓展提高3、函数y=(m – 1)x+1是一次函数,且y随自变量x增大而减小,那么m的取值__________ m<12、函数y=2-3x,y随x的增大而______ .减小1、一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为( )C之体验成功
5、已知一次函数y=(1-2k)x+k的函数值y随x的增大而增大,且图象经过一、二、三象限,则k的取值范围是__________.6、若直线y=kx+b平行直线y=3x+2且在y轴上的的交点坐标为 (0, 5) 则k= ,b= 。354、已知一次函数y=2x+4的图象上有两点
A(3,a),B(4,b),则a与b的大小关系为_______a
选做:104页12谢谢大家拓展与应用1、一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为( )C例 题例1、已知函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
这时它的图象经过哪些象限?
(2)当 m取何值时,y随x的增大而减小?
这时它的图象经过哪些象限?解:当m+1>0即m>-1时y随x的增大而增大,当m+1<0即m<-1时y随x的增大而减小,这时它的图象经过一、三、四象限
这时它的图象经过二、三、四象限
AB1、掌握一次函数y=kx+b的性质。 2、利用一次函数y=kx+b的图象与性质解决有关问题。之我要学什么
