人教版九年级上册数学22.3实际问题与二次函数 课时作业(无答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数 课时作业(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 267.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 06:51:14 | ||
图片预览

文档简介
人教版九年级上册数学22.3实际问题与二次函数 课时作业
一、单选题
1.游乐场里的过山车是很多人喜欢的项目.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,其运行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系().如图记录了过山车在该路段运行的水平距离x与y的三组数据A、B、C,根据上述函数模型和数据,可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.5 B.6 C.7 D.9
2.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10 B.20 C.30 D.10或30
3.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1) ,(,y2)是抛物线上的两点,则y1<y2.其中正确的结论有
A.4个 B.3个 C.2个 D.1个
4.2022年9月29日国产大飞机C919从上海浦东机场第四跑道起飞,并于9时54分安全着陆,这标志着我国具备了按照国际通行适航标准研制大型客机的能力,如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则该飞机着陆后滑行最长时间为( )
A.243秒 B.486秒 C.18秒 D.36秒
5.从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)之间的关系式是h=30t﹣5t2(0≤t≤6),则小球最高时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
6.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
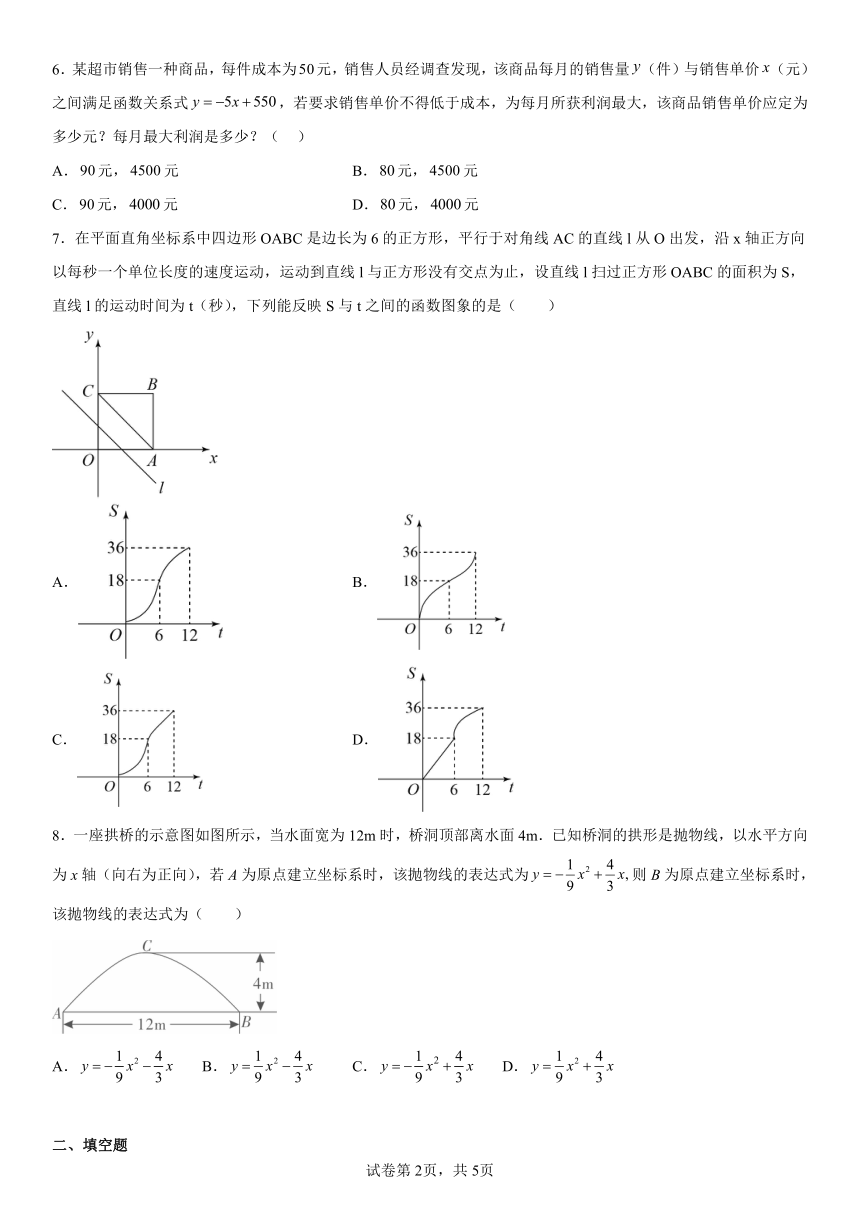
7.在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
A. B.
C. D.
8.一座拱桥的示意图如图所示,当水面宽为12m时,桥洞顶部离水面4m.已知桥洞的拱形是抛物线,以水平方向为x轴(向右为正向),若A为原点建立坐标系时,该抛物线的表达式为则B为原点建立坐标系时,该抛物线的表达式为( )
A. B. C. D.
二、填空题
9.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:s)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间_________s.
10.如图,小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为 ___________ m.
11.如图,某大门的形状是一抛物线形建筑,大门的地面宽8m,在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6m.若按图所示建立平面直角坐标系,则抛物线的解析式是____________.(建筑物厚度忽略不计)
12.某商品的销售利润y与销售单价x的关系为y=+2650,则当x=___元时,y有最_______值,这个值为______元.
13.用木料制作成一个如图所示的“目”形长方形大窗框(横档,也用木料,其中,要使窗框的面积最大,则的长为___________m.
三、解答题
14.如图,若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系为,请根据要求解答下列问题:
(1)在飞行过程中,小球从飞出到落地所用时间是多少
(2)在飞行过程中,小球飞行高度何时最大 最大高度是多少
15.如图所示,有一座抛物线形拱桥,桥下水面在正常水位时,宽16米,此时水面距拱顶4米.
(1)在如图所示的坐标系中,求抛物线的解析式;
(2)若水位上升3米,就达到警戒线,则拱桥内水面的宽是多少米?
16.如图,在中,,,点P从点A出发,以cm/s的速度沿向终点B运动.过点P作与Q,当点P不与A、B重合时,以线段为边向右作长方形,使.设长方形与的重叠面积为S,点P的运动时间为t(s).
(1)用含t的代数式表示线段的长度.
(2)连接,当平分的面积时,求出t的值.
(3)当点N落在边上时,求t的值.
(4)用含t的代数式表示S.
17.某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价2元,商场平均每天可多售出5件.求:
(1)若商场平均每天要赢利1400元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
试卷第2页,共2页
试卷第1页,共1页
一、单选题
1.游乐场里的过山车是很多人喜欢的项目.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,其运行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系().如图记录了过山车在该路段运行的水平距离x与y的三组数据A、B、C,根据上述函数模型和数据,可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.5 B.6 C.7 D.9
2.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10 B.20 C.30 D.10或30
3.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1) ,(,y2)是抛物线上的两点,则y1<y2.其中正确的结论有
A.4个 B.3个 C.2个 D.1个
4.2022年9月29日国产大飞机C919从上海浦东机场第四跑道起飞,并于9时54分安全着陆,这标志着我国具备了按照国际通行适航标准研制大型客机的能力,如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则该飞机着陆后滑行最长时间为( )
A.243秒 B.486秒 C.18秒 D.36秒
5.从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)之间的关系式是h=30t﹣5t2(0≤t≤6),则小球最高时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
6.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
7.在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
A. B.
C. D.
8.一座拱桥的示意图如图所示,当水面宽为12m时,桥洞顶部离水面4m.已知桥洞的拱形是抛物线,以水平方向为x轴(向右为正向),若A为原点建立坐标系时,该抛物线的表达式为则B为原点建立坐标系时,该抛物线的表达式为( )
A. B. C. D.
二、填空题
9.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:s)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间_________s.
10.如图,小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为 ___________ m.
11.如图,某大门的形状是一抛物线形建筑,大门的地面宽8m,在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6m.若按图所示建立平面直角坐标系,则抛物线的解析式是____________.(建筑物厚度忽略不计)
12.某商品的销售利润y与销售单价x的关系为y=+2650,则当x=___元时,y有最_______值,这个值为______元.
13.用木料制作成一个如图所示的“目”形长方形大窗框(横档,也用木料,其中,要使窗框的面积最大,则的长为___________m.
三、解答题
14.如图,若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系为,请根据要求解答下列问题:
(1)在飞行过程中,小球从飞出到落地所用时间是多少
(2)在飞行过程中,小球飞行高度何时最大 最大高度是多少
15.如图所示,有一座抛物线形拱桥,桥下水面在正常水位时,宽16米,此时水面距拱顶4米.
(1)在如图所示的坐标系中,求抛物线的解析式;
(2)若水位上升3米,就达到警戒线,则拱桥内水面的宽是多少米?
16.如图,在中,,,点P从点A出发,以cm/s的速度沿向终点B运动.过点P作与Q,当点P不与A、B重合时,以线段为边向右作长方形,使.设长方形与的重叠面积为S,点P的运动时间为t(s).
(1)用含t的代数式表示线段的长度.
(2)连接,当平分的面积时,求出t的值.
(3)当点N落在边上时,求t的值.
(4)用含t的代数式表示S.
17.某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价2元,商场平均每天可多售出5件.求:
(1)若商场平均每天要赢利1400元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
试卷第2页,共2页
试卷第1页,共1页
同课章节目录
