第18章《平行四边形》单元测试(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1. 如图,在平行四边形 中,下列说法一定正确的是
A. B. C. D.
2. 如图,已知矩形 ,, 分别是 和 上的点,, 分别是 , 的中点,若 ,,则 的长为
A. B. C. D.
3. 已知 为矩形 的对角线,则图中 与 一定不相等的是
A. B.
C. D.
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8,如图4,菱形花坛 ABCD的边长为 6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )
A.12m B.20m C.22m D.24m
9.如图,在中,,点在斜边上,且,则下列结论中错误的结论是
A. B. C. D.
10.将2021个形状、大小均相同的菱形按照如图所示的方式排成一列,使得右侧菱形的顶点与左侧菱形的对角线交点重合,若这些菱形的边长均为2,则阴影部分的周长总和等于( )
A.4042 B.8076 C.8080 D.8084
二、填空题(每题3分,共30分)
11. 已知平行四边形 中,,,那么这个平行四边形的周长为 .
12. 如图,菱形 的边长为 , 是 的中点,且 ,则菱形 的面积为 .
13. 在矩形 中,对角线 , 相交于点 ,,垂足为 ,如果 ,,那么 .
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
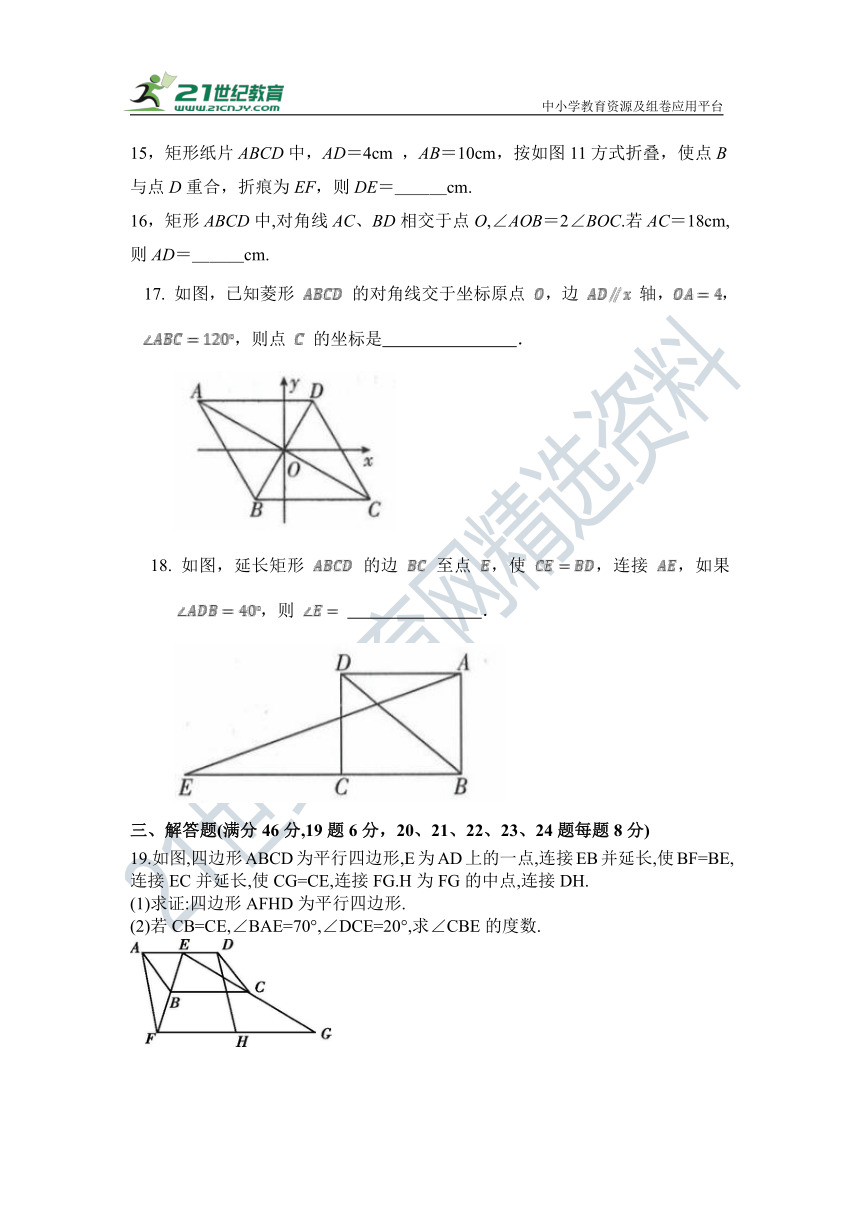
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17. 如图,已知菱形 的对角线交于坐标原点 ,边 轴,,,则点 的坐标是 .
18. 如图,延长矩形 的边 至点 ,使 ,连接 ,如果 ,则 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形.
(2)若CB=CE,∠BAE=70°,∠DCE=20°,求∠CBE的度数.
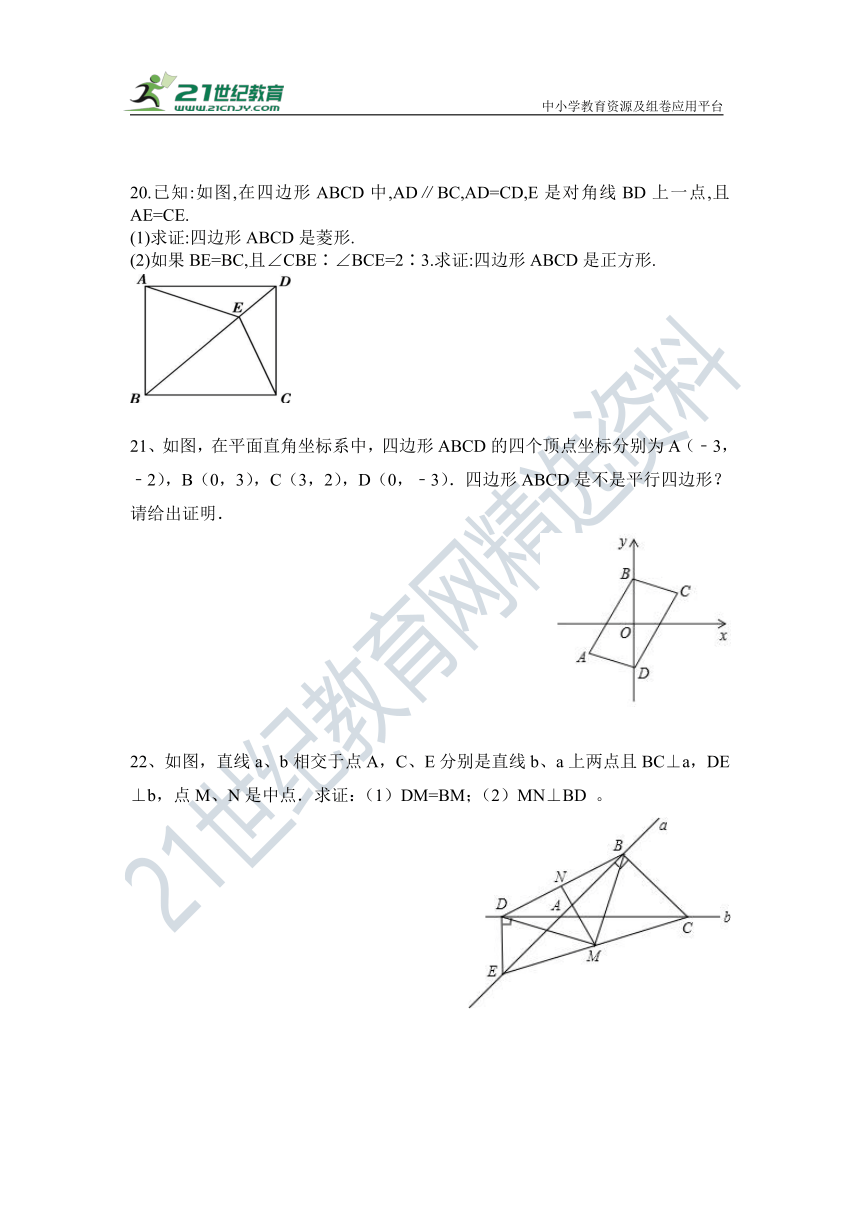
20.已知:如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且AE=CE.
(1)求证:四边形ABCD是菱形.
(2)如果BE=BC,且∠CBE∶∠BCE=2∶3.求证:四边形ABCD是正方形.
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23. 如图,在平行四边形 中,对角线 与 相交于点 ,点 , 分别为 , 的中点,延长 至 ,使 ,连接 .
(1)求证:.
(2)当 时,四边形 是什么样的四边形 试说明理由.
24. 如图①,在矩形纸片 中,,,折叠纸片使 点落在边 上的 处,折痕为 ,过点 作 交 于点 ,连接 .
(1)求证:四边形 为菱形;
(2)当点 在 边上移动时,折痕的端点 , 也随之移动.
①当点 与点 重合时(如图②),求菱形 的边长;
②若限定 , 分别在边 , 上移动,求出点 在边 上移动的最大距离.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D C D D D B D C
二、填空题(每题3分,共24分)
11.
12.
13.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17.
18.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19..(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAE=∠BCD.
∵BF=BE,CG=CE,∴BC是△EFG的中位线,
∴BC∥FG,BC=1/2FG.
∵H为FG的中点,∴FH=1/2FG,
∴BC∥FH,BC=FH,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形.
(2)解:∵∠BAE=70°,∴∠BCD=70°,
∵∠DCE=20°,∴∠BCE=70°-20°=50°.
∵CB=CE,
∴∠CBE=∠CEB=1/2(180°-50°)=65°.
20.证明:(1)在△ADE和△CDE中,{■(AD=CD,@DE=DE,@AE=CE,)┤
∴△ADE≌△CDE,∴∠ADE=∠CDE.
在△ABD和△CBD中,{■(AD=CD,@∠ADB=∠CDB,@BD=BD,)┤
∴△ABD≌△CBD,∴AB=CB.
∵AD∥BC,∴∠ADB=∠CBD=∠CDB,
∴BC=CD,∴AB=BC=CD=AD,
∴四边形ABCD是菱形.
(2)∵BE=BC,∴∠BCE=∠BEC.
设∠BCE=∠BEC=3x°,则∠CBE=2x°.
根据三角形内角和定理,得2x°+3x°+3x°=180°,
解得x=22.5,∴∠CBE=45°.
∵△ABD≌△CBD,
∴∠ABE=∠CBE=45°,∴∠ABC=90°,
又∵四边形ABCD是菱形,
∴四边形ABCD是正方形.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23. (1) 四边形 是平行四边形,
,,,,
.
点 , 分别为 , 的中点,
,,
.
在 和 中,
.
(2) 当 时,四边形 是矩形.理由如下:
,,
.
是 的中点,
,
.
同理:,
,
.
,,
是 的中位线,
,
,
四边形 是平行四边形.
,
平行四边形 是矩形.
24. (1) 折叠纸片使 点落在边 上的 处,折痕为 ,
点 与点 关于 对称,
,,.
又 ,
,
,
,
,
四边形 为菱形.
(2) ① 四边形 是矩形,
,,.
点 与点 关于 对称,
.
在 中,,
.
在 中,,
,
,
解得 ,
菱形 的边长为 .
②当点 与点 重合时,如图①.
此时点 离点 最近,由①知,此时 .
当点 与点 重合时,如图②.
此时点 离点 最远,此时四边形 为正方形,,
点 在边 上移动的最大距离为 .
图4
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1. 如图,在平行四边形 中,下列说法一定正确的是
A. B. C. D.
2. 如图,已知矩形 ,, 分别是 和 上的点,, 分别是 , 的中点,若 ,,则 的长为
A. B. C. D.
3. 已知 为矩形 的对角线,则图中 与 一定不相等的是
A. B.
C. D.
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8,如图4,菱形花坛 ABCD的边长为 6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )
A.12m B.20m C.22m D.24m
9.如图,在中,,点在斜边上,且,则下列结论中错误的结论是
A. B. C. D.
10.将2021个形状、大小均相同的菱形按照如图所示的方式排成一列,使得右侧菱形的顶点与左侧菱形的对角线交点重合,若这些菱形的边长均为2,则阴影部分的周长总和等于( )
A.4042 B.8076 C.8080 D.8084
二、填空题(每题3分,共30分)
11. 已知平行四边形 中,,,那么这个平行四边形的周长为 .
12. 如图,菱形 的边长为 , 是 的中点,且 ,则菱形 的面积为 .
13. 在矩形 中,对角线 , 相交于点 ,,垂足为 ,如果 ,,那么 .
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17. 如图,已知菱形 的对角线交于坐标原点 ,边 轴,,,则点 的坐标是 .
18. 如图,延长矩形 的边 至点 ,使 ,连接 ,如果 ,则 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形.
(2)若CB=CE,∠BAE=70°,∠DCE=20°,求∠CBE的度数.
20.已知:如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且AE=CE.
(1)求证:四边形ABCD是菱形.
(2)如果BE=BC,且∠CBE∶∠BCE=2∶3.求证:四边形ABCD是正方形.
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23. 如图,在平行四边形 中,对角线 与 相交于点 ,点 , 分别为 , 的中点,延长 至 ,使 ,连接 .
(1)求证:.
(2)当 时,四边形 是什么样的四边形 试说明理由.
24. 如图①,在矩形纸片 中,,,折叠纸片使 点落在边 上的 处,折痕为 ,过点 作 交 于点 ,连接 .
(1)求证:四边形 为菱形;
(2)当点 在 边上移动时,折痕的端点 , 也随之移动.
①当点 与点 重合时(如图②),求菱形 的边长;
②若限定 , 分别在边 , 上移动,求出点 在边 上移动的最大距离.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D C D D D B D C
二、填空题(每题3分,共24分)
11.
12.
13.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17.
18.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19..(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAE=∠BCD.
∵BF=BE,CG=CE,∴BC是△EFG的中位线,
∴BC∥FG,BC=1/2FG.
∵H为FG的中点,∴FH=1/2FG,
∴BC∥FH,BC=FH,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形.
(2)解:∵∠BAE=70°,∴∠BCD=70°,
∵∠DCE=20°,∴∠BCE=70°-20°=50°.
∵CB=CE,
∴∠CBE=∠CEB=1/2(180°-50°)=65°.
20.证明:(1)在△ADE和△CDE中,{■(AD=CD,@DE=DE,@AE=CE,)┤
∴△ADE≌△CDE,∴∠ADE=∠CDE.
在△ABD和△CBD中,{■(AD=CD,@∠ADB=∠CDB,@BD=BD,)┤
∴△ABD≌△CBD,∴AB=CB.
∵AD∥BC,∴∠ADB=∠CBD=∠CDB,
∴BC=CD,∴AB=BC=CD=AD,
∴四边形ABCD是菱形.
(2)∵BE=BC,∴∠BCE=∠BEC.
设∠BCE=∠BEC=3x°,则∠CBE=2x°.
根据三角形内角和定理,得2x°+3x°+3x°=180°,
解得x=22.5,∴∠CBE=45°.
∵△ABD≌△CBD,
∴∠ABE=∠CBE=45°,∴∠ABC=90°,
又∵四边形ABCD是菱形,
∴四边形ABCD是正方形.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23. (1) 四边形 是平行四边形,
,,,,
.
点 , 分别为 , 的中点,
,,
.
在 和 中,
.
(2) 当 时,四边形 是矩形.理由如下:
,,
.
是 的中点,
,
.
同理:,
,
.
,,
是 的中位线,
,
,
四边形 是平行四边形.
,
平行四边形 是矩形.
24. (1) 折叠纸片使 点落在边 上的 处,折痕为 ,
点 与点 关于 对称,
,,.
又 ,
,
,
,
,
四边形 为菱形.
(2) ① 四边形 是矩形,
,,.
点 与点 关于 对称,
.
在 中,,
.
在 中,,
,
,
解得 ,
菱形 的边长为 .
②当点 与点 重合时,如图①.
此时点 离点 最近,由①知,此时 .
当点 与点 重合时,如图②.
此时点 离点 最远,此时四边形 为正方形,,
点 在边 上移动的最大距离为 .
图4
