2023年高考数学二轮复习专题课件★★导数与不等式恒(能)成立问题 课件(共28张PPT)
文档属性
| 名称 | 2023年高考数学二轮复习专题课件★★导数与不等式恒(能)成立问题 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 626.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 09:21:20 | ||
图片预览


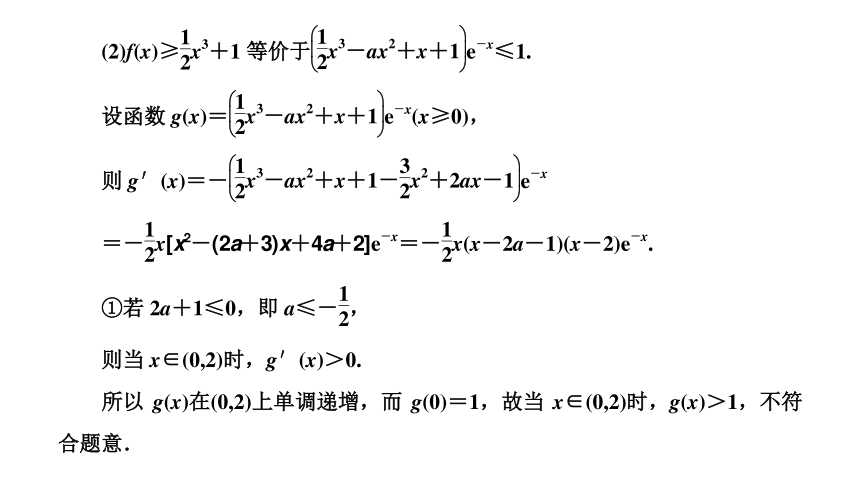

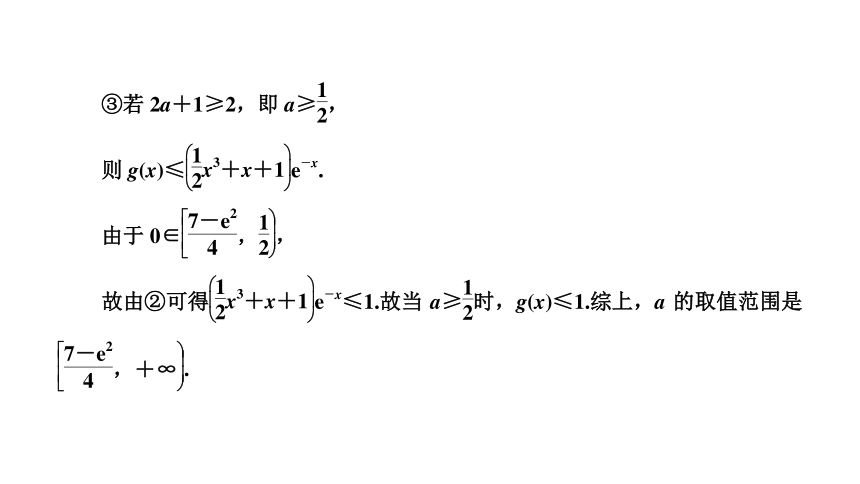




文档简介
(共28张PPT)
2023年高考数学二轮复习专题课件★★ 导数与不等式恒(能)成立问题
命题点(一) 分类讨论解决不等式恒成立问题
近几年高考中利用导数解决不等式恒成立问题是常见的题型,函数中经常含有参数,对参数进行分类讨论解决问题,主要在解答题中以压轴题的形式出现,考查学生的逻辑推理能力和计算能力,题目的综合性较强,难度大.
[关键点拨]
切入点 (1)构造函数m(x),判断f′(x)的单调性,进而判断f(x)的单调性
(2)构造函数,把不等式的恒成立问题转化为函数的最值问题
障碍点 不能把导函数正确的分解因式,分类讨论的标准不可解
[解] (1)当a=1时,f(x)=ex+x2-x,f′(x)=ex+2x-1.令m(x)=f′(x)=ex+2x-1,
则m′(x)=ex+2>0.
所以m(x)在R上单调递增,
即f′(x)在R上单调递增.
注意到f′(0)=0,
故当x∈(-∞,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
所以f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
不等式恒成立问题的解题关键点
已知函数f(x)=ln x-ax,a∈R.
(1)求函数f(x)的单调区间;
(2)若不等式f(x)+a<0在x∈(1,+∞)上恒成立,求a的取值范围.
分离参数法的主要思想是将不等式变形成一个一端是参数a,另一端是变量表达式v(x)的不等式后,应用数形结合思想把不等式恒成立问题转化为水平直线y=a与函数y=v(x)图象的交点个数问题来解决.
根据不等式能成立求参数的步骤
(1)利用题设条件将问题转化为某函数在该区间上最大(小)值满足的不等式的能成立问题;
(2)用导数求该函数在区间上的最值;
(3)构建不等式求解.
已知函数f(x)=(x-1)ex-ax-1.
(1)当a>0时,证明函数f(x)在区间(0, +∞)上只有一个零点;
(2)若存在x∈R,使不等式f(x)<-e-1成立,求a的取值范围.
解:(1)证明:当a>0时,f′(x)=xex-a,x∈(0, +∞),
令g(x)= f′(x),则g′(x)=(x+1)ex>0,∴f′(x)=xex-a在(0,+∞)上为增函数,
∵f′(0)=-a<0, f′(a)=aea-a>0,∴ x0∈(0,a),使f′(x0)=x0ex0-a=0,
∴当x∈(0, x0)时,f′(x)<0;当x∈(x0, +∞)时,f′(x)>0,
因此,f(x)在(0, x0)上为减函数,f(x)在(x0, +∞)上为增函数,
2023年高考数学二轮复习专题课件★★ 导数与不等式恒(能)成立问题
命题点(一) 分类讨论解决不等式恒成立问题
近几年高考中利用导数解决不等式恒成立问题是常见的题型,函数中经常含有参数,对参数进行分类讨论解决问题,主要在解答题中以压轴题的形式出现,考查学生的逻辑推理能力和计算能力,题目的综合性较强,难度大.
[关键点拨]
切入点 (1)构造函数m(x),判断f′(x)的单调性,进而判断f(x)的单调性
(2)构造函数,把不等式的恒成立问题转化为函数的最值问题
障碍点 不能把导函数正确的分解因式,分类讨论的标准不可解
[解] (1)当a=1时,f(x)=ex+x2-x,f′(x)=ex+2x-1.令m(x)=f′(x)=ex+2x-1,
则m′(x)=ex+2>0.
所以m(x)在R上单调递增,
即f′(x)在R上单调递增.
注意到f′(0)=0,
故当x∈(-∞,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
所以f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
不等式恒成立问题的解题关键点
已知函数f(x)=ln x-ax,a∈R.
(1)求函数f(x)的单调区间;
(2)若不等式f(x)+a<0在x∈(1,+∞)上恒成立,求a的取值范围.
分离参数法的主要思想是将不等式变形成一个一端是参数a,另一端是变量表达式v(x)的不等式后,应用数形结合思想把不等式恒成立问题转化为水平直线y=a与函数y=v(x)图象的交点个数问题来解决.
根据不等式能成立求参数的步骤
(1)利用题设条件将问题转化为某函数在该区间上最大(小)值满足的不等式的能成立问题;
(2)用导数求该函数在区间上的最值;
(3)构建不等式求解.
已知函数f(x)=(x-1)ex-ax-1.
(1)当a>0时,证明函数f(x)在区间(0, +∞)上只有一个零点;
(2)若存在x∈R,使不等式f(x)<-e-1成立,求a的取值范围.
解:(1)证明:当a>0时,f′(x)=xex-a,x∈(0, +∞),
令g(x)= f′(x),则g′(x)=(x+1)ex>0,∴f′(x)=xex-a在(0,+∞)上为增函数,
∵f′(0)=-a<0, f′(a)=aea-a>0,∴ x0∈(0,a),使f′(x0)=x0ex0-a=0,
∴当x∈(0, x0)时,f′(x)<0;当x∈(x0, +∞)时,f′(x)>0,
因此,f(x)在(0, x0)上为减函数,f(x)在(x0, +∞)上为增函数,
同课章节目录
