人教版八年级下册18.1.2平行四边形的判定(第2课时) 课件(共31张PPT)
文档属性
| 名称 | 人教版八年级下册18.1.2平行四边形的判定(第2课时) 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 19:14:31 | ||
图片预览





文档简介
(共31张PPT)
平行四边形的判定
1、平行四边形的定义是什么 有什么作用
2、平行四边形有哪些性质
平行四边形的性质:
边:
角:
对角线:
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
温故知新
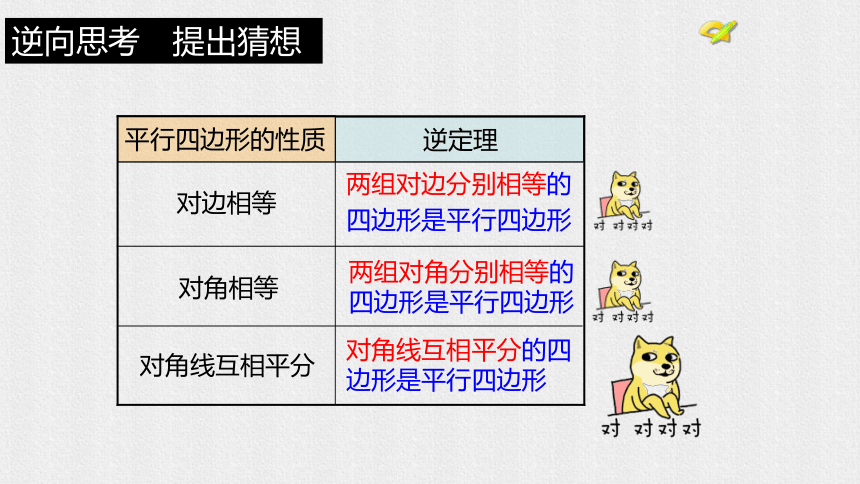
逆向思考 提出猜想
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
逆定理
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
除了由性质推出来的判定外
还有其他证明平行四边形的方法吗?
问题来了:
小明的爸爸
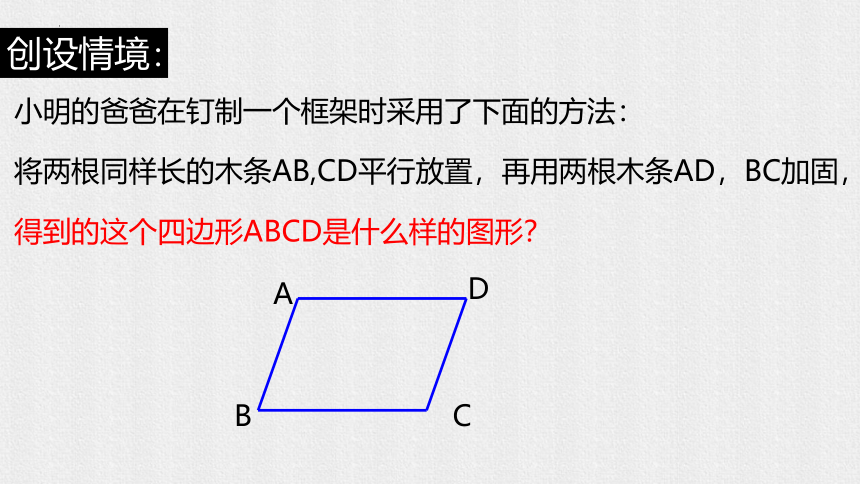
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,
得到的这个四边形ABCD是什么样的图形?
创设情境:
A
B
C
D
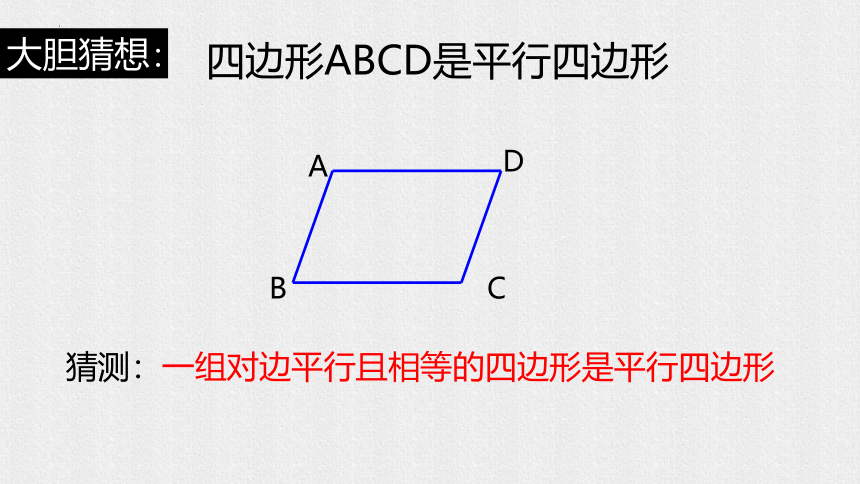
四边形ABCD是平行四边形
猜测:一组对边平行且相等的四边形是平行四边形
A
B
C
D
大胆猜想:
A
D
C
B
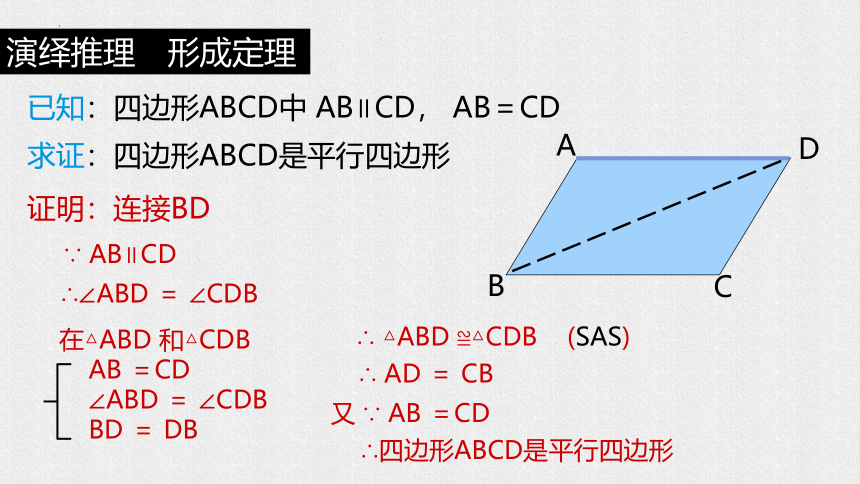
已知:四边形ABCD中 AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
在△ABD 和△CDB
AB =CD
∠ABD = ∠CDB
BD = DB
∴ △ABD ≌△CDB (SAS)
∴ AD = CB
∴四边形ABCD是平行四边形
又 ∵ AB =CD
演绎推理 形成定理
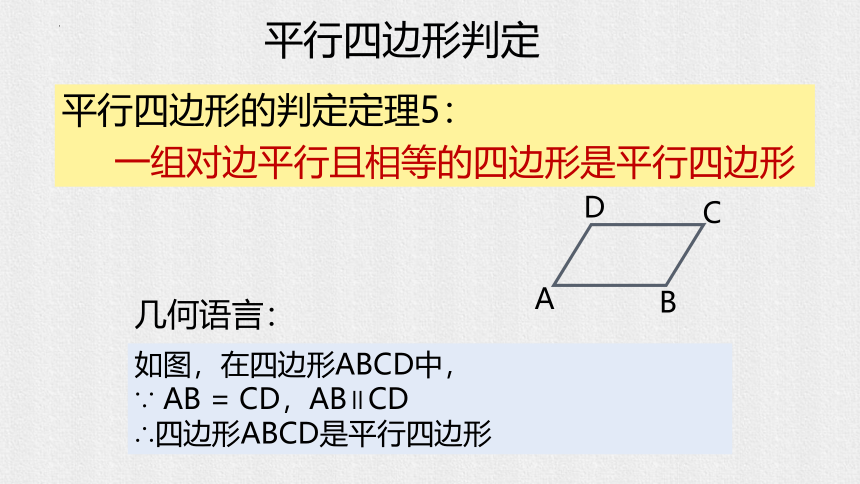
如图,在四边形ABCD中,
∵ AB = CD,AB∥CD
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理5:
一组对边平行且相等的四边形是平行四边形
几何语言:
C
A
D
B
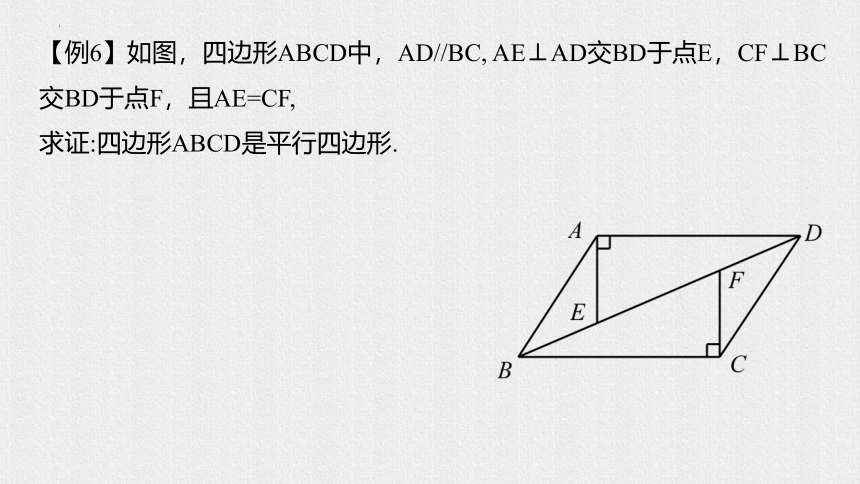
【例6】如图,四边形ABCD中,AD//BC, AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF,
求证:四边形ABCD是平行四边形.
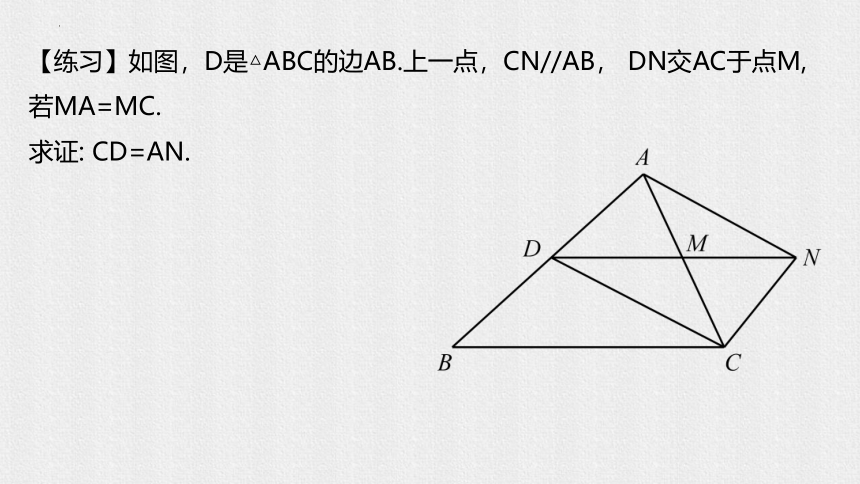
【练习】如图,D是△ABC的边AB.上一点,CN//AB, DN交AC于点M,若MA=MC.
求证: CD=AN.
综合运用
五种判定方法(重点)
判定方法 条件
从边考虑
从角考虑
从对角线考虑
两组对边分别平行
两组对边分别相等
一组对边平行且相等
两组对角分别相等
对角线互相平分
综合运用
五种判定方法
两组对边
分别平行
两组对边
分别相等
一组对边
平行且相等
两组对角
分别相等
对角线
互相平分
注:颜色相等表示平行,
画短线表示边相等
【例7】下列命题中,正确的是( )
A.两组角相等的四边形是平行四边形
B.一组对边相等,两条对角线相等的四边形是平行四边形
C.一条对角线平分另一条对角线的四边形是平行四边形
D.两组对边分别相等的四边形是平行四边形
【练习】如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A. AB=DC,AD=BC .
B. AB//DC, AD//BC
C. AB//DC,AD=BC
D. AB//DC, AB=DC
【例8】如图,平行四边形ABCD中,点E、F在对角线AC上,请你添加一个适当的条件:____________________,使四边形DEBF是平行四边形。
ED=BF(一组对边平行且相等)
BE∥DF(两组对边平行)
【练习】如图,ABCD中,E, F分别为BC, AD边.上的点,要使四边形BEDF为平行四边形,需添加一个条件:________________
【例9】四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD//BC;②AD=BC;③OA=OC;④OB=OD从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A. 3种 B. 4种 C. 5种 D. 6种
【例10】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30° ,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
完成课本P47页练习
三角形的中位线
D
E
A
B
C
定义:连接三角形两边中点的线段叫作三角形的中位线
三角形的中位线定理
D
E
A
B
C
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
【例11】如图,在△ABC中,点D, E分别是AB, AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A. 50° B. 60° C. 70° D. 80°
【练习】直角三角形两条直角边长分别是6和8,则连接两条直角边中点的线段长是( )
A.10 B. 3 C. 4 D. 5
【练习】△ABC中的三条中位线围成的三角形周长是15cm,则△ABC的周长为( )
A.60cm B. 45cm C. 30cm D.
【例12】△ABC的三边长分别为a、b、c,三条中位线组成第一个中点三角形,第一个中点三角形的三条中位线又组成第二个中点三角形,以此类推,求第2015中点三角形的周长为( )
A. B. C. D.
【例13】如图,△ABC的周长为26,点D, E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为__________
【例13】如图,在△ABC中,M为BC中点, AN平分∠BAC, AN⊥BN于N,且AB=10, AC=16,则MN
等于( )
B.
C.
D.
【例14】如图,在Rt△ABC中,∠BAC=90°, E, F分别是BC, AC的中点,延长BA到点D,使AD=AB.连接DE,DF.
(1)求证: AF与DE互相平分;
(2)若BC=4,求DF的长.
【练习】如图所示,在四边形ABCD中,AD=BC, P是对角线BD的中点,M是DC的中点,N是AB的中点.
请判断△PMN的形状,并说明理由.
完成课本P49页练习
练习册20-21页
下课
课
后
作
业
平行四边形的判定
1、平行四边形的定义是什么 有什么作用
2、平行四边形有哪些性质
平行四边形的性质:
边:
角:
对角线:
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
温故知新
逆向思考 提出猜想
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
逆定理
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
除了由性质推出来的判定外
还有其他证明平行四边形的方法吗?
问题来了:
小明的爸爸
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,
得到的这个四边形ABCD是什么样的图形?
创设情境:
A
B
C
D
四边形ABCD是平行四边形
猜测:一组对边平行且相等的四边形是平行四边形
A
B
C
D
大胆猜想:
A
D
C
B
已知:四边形ABCD中 AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
在△ABD 和△CDB
AB =CD
∠ABD = ∠CDB
BD = DB
∴ △ABD ≌△CDB (SAS)
∴ AD = CB
∴四边形ABCD是平行四边形
又 ∵ AB =CD
演绎推理 形成定理
如图,在四边形ABCD中,
∵ AB = CD,AB∥CD
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理5:
一组对边平行且相等的四边形是平行四边形
几何语言:
C
A
D
B
【例6】如图,四边形ABCD中,AD//BC, AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF,
求证:四边形ABCD是平行四边形.
【练习】如图,D是△ABC的边AB.上一点,CN//AB, DN交AC于点M,若MA=MC.
求证: CD=AN.
综合运用
五种判定方法(重点)
判定方法 条件
从边考虑
从角考虑
从对角线考虑
两组对边分别平行
两组对边分别相等
一组对边平行且相等
两组对角分别相等
对角线互相平分
综合运用
五种判定方法
两组对边
分别平行
两组对边
分别相等
一组对边
平行且相等
两组对角
分别相等
对角线
互相平分
注:颜色相等表示平行,
画短线表示边相等
【例7】下列命题中,正确的是( )
A.两组角相等的四边形是平行四边形
B.一组对边相等,两条对角线相等的四边形是平行四边形
C.一条对角线平分另一条对角线的四边形是平行四边形
D.两组对边分别相等的四边形是平行四边形
【练习】如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A. AB=DC,AD=BC .
B. AB//DC, AD//BC
C. AB//DC,AD=BC
D. AB//DC, AB=DC
【例8】如图,平行四边形ABCD中,点E、F在对角线AC上,请你添加一个适当的条件:____________________,使四边形DEBF是平行四边形。
ED=BF(一组对边平行且相等)
BE∥DF(两组对边平行)
【练习】如图,ABCD中,E, F分别为BC, AD边.上的点,要使四边形BEDF为平行四边形,需添加一个条件:________________
【例9】四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD//BC;②AD=BC;③OA=OC;④OB=OD从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A. 3种 B. 4种 C. 5种 D. 6种
【例10】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30° ,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
完成课本P47页练习
三角形的中位线
D
E
A
B
C
定义:连接三角形两边中点的线段叫作三角形的中位线
三角形的中位线定理
D
E
A
B
C
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
【例11】如图,在△ABC中,点D, E分别是AB, AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A. 50° B. 60° C. 70° D. 80°
【练习】直角三角形两条直角边长分别是6和8,则连接两条直角边中点的线段长是( )
A.10 B. 3 C. 4 D. 5
【练习】△ABC中的三条中位线围成的三角形周长是15cm,则△ABC的周长为( )
A.60cm B. 45cm C. 30cm D.
【例12】△ABC的三边长分别为a、b、c,三条中位线组成第一个中点三角形,第一个中点三角形的三条中位线又组成第二个中点三角形,以此类推,求第2015中点三角形的周长为( )
A. B. C. D.
【例13】如图,△ABC的周长为26,点D, E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为__________
【例13】如图,在△ABC中,M为BC中点, AN平分∠BAC, AN⊥BN于N,且AB=10, AC=16,则MN
等于( )
B.
C.
D.
【例14】如图,在Rt△ABC中,∠BAC=90°, E, F分别是BC, AC的中点,延长BA到点D,使AD=AB.连接DE,DF.
(1)求证: AF与DE互相平分;
(2)若BC=4,求DF的长.
【练习】如图所示,在四边形ABCD中,AD=BC, P是对角线BD的中点,M是DC的中点,N是AB的中点.
请判断△PMN的形状,并说明理由.
完成课本P49页练习
练习册20-21页
下课
课
后
作
业
