垂径定理[上学期]
图片预览

文档简介
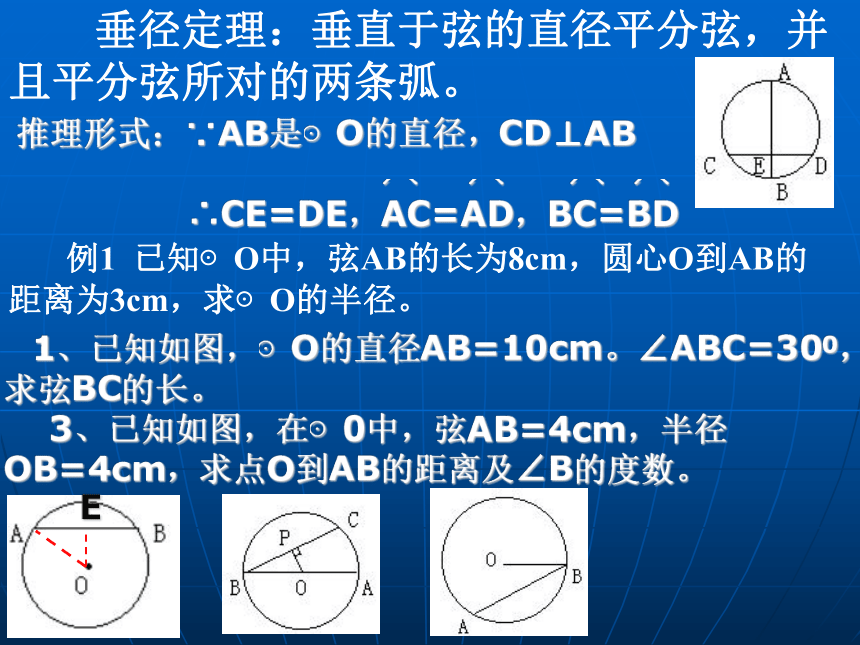
课件18张PPT。垂径定理安岳外国语学校 龙 强 垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。 推理形式:∵AB是⊙O的直径,CD⊥AB
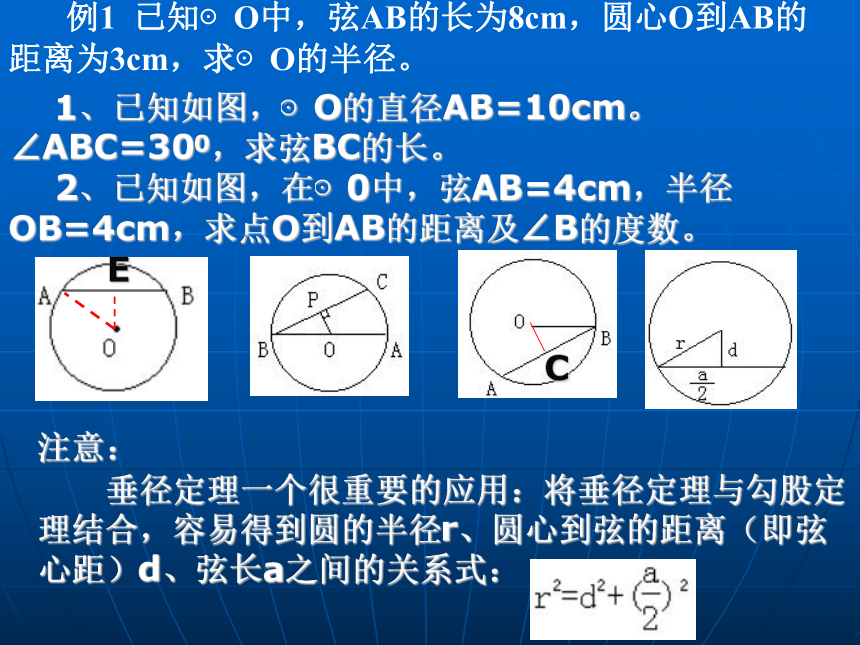
∴CE=DE,AC=AD,BC=BD ⌒⌒⌒⌒ 例1 已知⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。 E 1、已知如图,⊙O的直径AB=10cm。∠ABC=300,求弦BC的长。
3、已知如图,在⊙0中,弦AB=4cm,半径OB=4cm,求点O到AB的距离及∠B的度数。 例1 已知⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。 1、已知如图,⊙O的直径AB=10cm。∠ABC=300,求弦BC的长。
2、已知如图,在⊙0中,弦AB=4cm,半径OB=4cm,求点O到AB的距离及∠B的度数。EC注意:
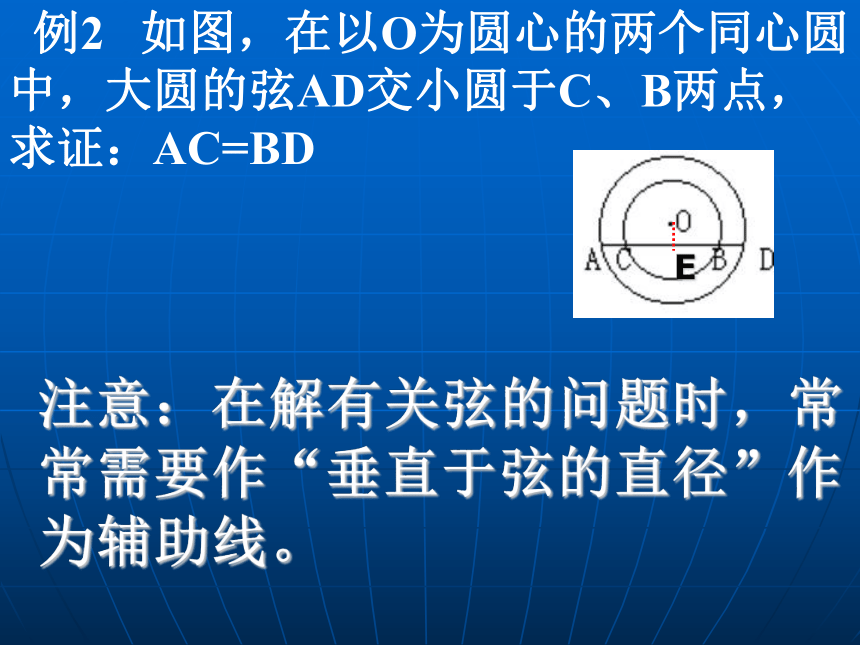
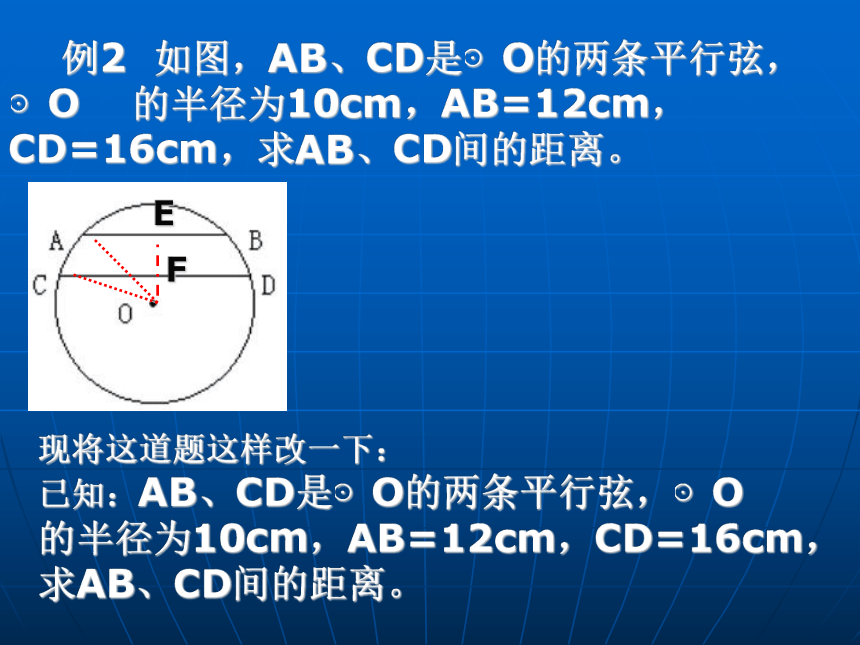
垂径定理一个很重要的应用:将垂径定理与勾股定理结合,容易得到圆的半径r、圆心到弦的距离(即弦心距)d、弦长a之间的关系式: 例2 如图,在以O为圆心的两个同心圆中,大圆的弦AD交小圆于C、B两点,求证:AC=BD E注意:在解有关弦的问题时,常常需要作“垂直于弦的直径”作为辅助线。 例2 如图,AB、CD是⊙O的两条平行弦,⊙O 的半径为10cm,AB=12cm,CD=16cm,求AB、CD间的距离。EF现将这道题这样改一下:
已知:AB、CD是⊙O的两条平行弦,⊙O 的半径为10cm,AB=12cm,CD=16cm,求AB、CD间的距离。练习:
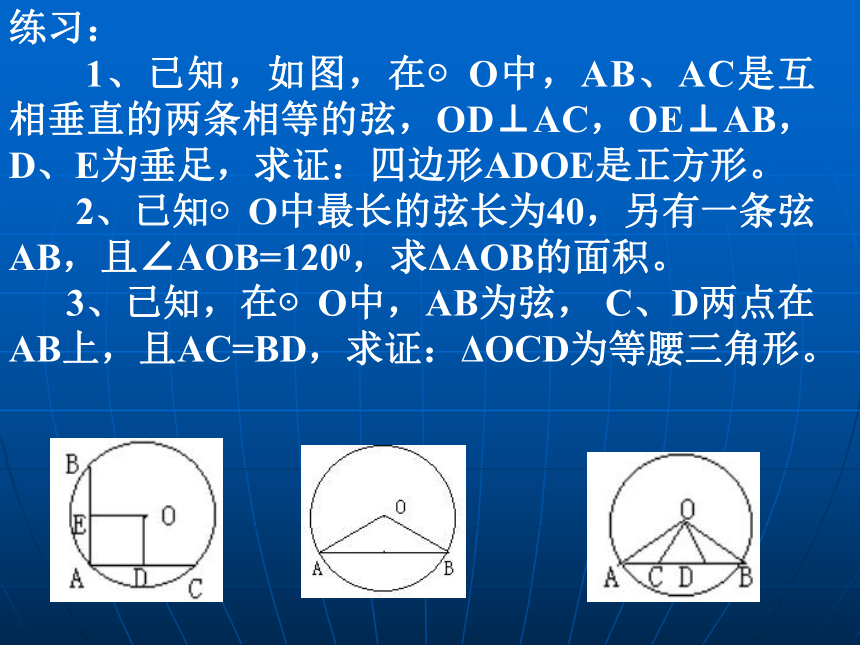
1、已知,如图,在⊙O中,AB、AC是互相垂直的两条相等的弦,OD⊥AC,OE⊥AB,D、E为垂足,求证:四边形ADOE是正方形。
2、已知⊙O中最长的弦长为40,另有一条弦AB,且∠AOB=1200,求ΔAOB的面积。
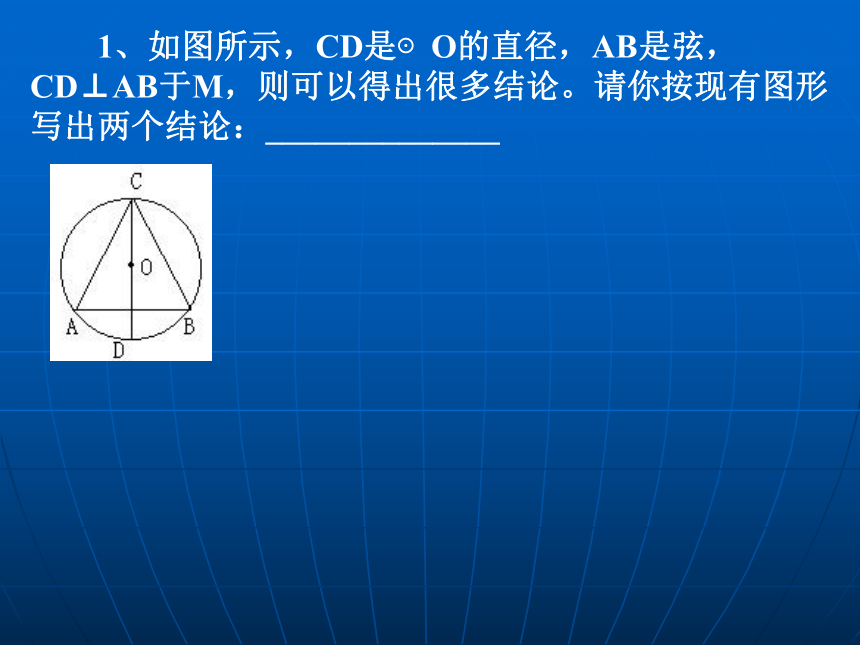
3、已知,在⊙O中,AB为弦, C、D两点在AB上,且AC=BD,求证:ΔOCD为等腰三角形。 1、如图所示,CD是⊙O的直径,AB是弦,CD⊥AB于M,则可以得出很多结论。请你按现有图形写出两个结论:______________(1)直径AB(2)AB ⊥ CD,垂足为H( 3 )CH=DH?将圆沿AB 对折,两个半圆互相重合因为CH=DH又因为?AHD+ ? AHC=180 ?
所以?AHD= ? AHC=90 ?
即AB ? CD条件:直径平分弦结论:这条直径垂直于弦,平分弦所对的弧。?推论:如果一条直径平分不是直径的弦,那么这条直径垂直于弦,平分弦所对的弧条件:直径平分不是直径的弦结论:垂直于弦,平分弦所对的弧你还能写出一些结论吗?试一试。(1)如果圆的直径平分弦(这条弦不是直径),那
么这条直径垂直这条弦,并且平分这条弦所对的弧。
(2)如果圆的直径平分弧,那么这条直径垂直平分
这条弧所对的弦。
(3)如果一条直线是弦的垂直平分线,那么这条直
线过圆心并且平分这条弦所对的弧。
(4)如果一条直线平分弦和它所对的一条弧,那么
这条直线过圆心并且垂直这条弦。
(5)如果一条直线垂直于弦并且平分弦所对的一条
弧,那么这条直线过圆心并且平分这条弦。一、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???例1 现有一块破碎的轮片,欲重新配制一块半径与其相等的圆形轮片,你准备采用什么方法? 例2 有位同学用下面的方法4等分AB: (1)连结AB (2)作AB的垂直平分线CD交AB于点M,并AB于点T。 (3)分别作AT、TB的垂直平分线EF、GH,交AB于N、P。 则N、M、P三点把AB4等分。 这位同学的作法对吗?⌒⌒⌒⌒例3 已知,AB、CD是⊙O的两条 弦,且AB//CD,求证:AC=BD⌒⌒OE 练习: 1、已知,如图1,⊙O的弦AB、CD的夹角为500,M、N分别是AB、CD的中点,求∠MON的度数。 2、如图2,⊙O1和⊙O2相交于A、B两点,过点A作O1O2的平行线交两圆于C、D,已知O1O2=20cm,求CD的长。 ⌒⌒EF 例4 AB、BC是⊙O的弦,且AB⊥BC,M、N分别是AB、BC的中点,OM、ON分别交AB、BC于D、E,若OD=4cm,OE=3cm,求: (1)AB、BC的长;(2)⊙O的半径。⌒⌒ 1、已知⊙O中,弦AB、CD互相垂直,AB被CD分成的两条线段的长分别为5cm和13cm,则圆心O到CD的距离为________cm。 2、已知,⊙O中,AB=BC=OC分别交AC、BD于E、F,求证△OEF为等腰三角形。⌒⌒⌒ 例5、如图,在扇形OAB中,C是弧AB的中点,OC交AB于点D ,?AOC=30 0,AD=16cm求(1) ?OAB的度数(2)AB的长ABCDODO 练习:某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦长)为40米,拱高(弧的中点到弦的距离)为8米,求拱桥的半径。弦a、弦心距d、半径r、弓形高h之间的关系: 1、r=d+h 2、注意:要先将实际问题转化为数学问题 1、在⊙O中,M是AB的中点,N是弦AB的中点, AB=4 ,MN=2,求圆心到O到AB的距离。 2、如图所示,⊙O的直径AB和弦CD相交于E,AE=6cm,EB=14cm,∠DEB=300,求CD的长。 3、在Rt△ABC中,∠ACB=900,AC=8,BC=6,若以C为圆心,CB为半径的圆交AB于点P,求AP的长。 4、AB为⊙O的弦,P为AB上一点,AB=10,AP=4,OP=5,求⊙O的半径。
1、已知,如图,在⊙O中,AB、AC是互相垂直的两条相等的弦,OD⊥AC,OE⊥AB,D、E为垂足,求证:四边形ADOE是正方形。
2、已知⊙O中最长的弦长为40,另有一条弦AB,且∠AOB=1200,求ΔAOB的面积。
3、已知,在⊙O中,AB为弦, C、D两点在AB上,且AC=BD,求证:ΔOCD为等腰三角形。 1、如图所示,CD是⊙O的直径,AB是弦,CD⊥AB于M,则可以得出很多结论。请你按现有图形写出两个结论:______________(1)直径AB(2)AB ⊥ CD,垂足为H( 3 )CH=DH?将圆沿AB 对折,两个半圆互相重合因为CH=DH又因为?AHD+ ? AHC=180 ?
所以?AHD= ? AHC=90 ?
即AB ? CD条件:直径平分弦结论:这条直径垂直于弦,平分弦所对的弧。?推论:如果一条直径平分不是直径的弦,那么这条直径垂直于弦,平分弦所对的弧条件:直径平分不是直径的弦结论:垂直于弦,平分弦所对的弧你还能写出一些结论吗?试一试。(1)如果圆的直径平分弦(这条弦不是直径),那
么这条直径垂直这条弦,并且平分这条弦所对的弧。
(2)如果圆的直径平分弧,那么这条直径垂直平分
这条弧所对的弦。
(3)如果一条直线是弦的垂直平分线,那么这条直
线过圆心并且平分这条弦所对的弧。
(4)如果一条直线平分弦和它所对的一条弧,那么
这条直线过圆心并且垂直这条弦。
(5)如果一条直线垂直于弦并且平分弦所对的一条
弧,那么这条直线过圆心并且平分这条弦。一、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???例1 现有一块破碎的轮片,欲重新配制一块半径与其相等的圆形轮片,你准备采用什么方法? 例2 有位同学用下面的方法4等分AB: (1)连结AB (2)作AB的垂直平分线CD交AB于点M,并AB于点T。 (3)分别作AT、TB的垂直平分线EF、GH,交AB于N、P。 则N、M、P三点把AB4等分。 这位同学的作法对吗?⌒⌒⌒⌒例3 已知,AB、CD是⊙O的两条 弦,且AB//CD,求证:AC=BD⌒⌒OE 练习: 1、已知,如图1,⊙O的弦AB、CD的夹角为500,M、N分别是AB、CD的中点,求∠MON的度数。 2、如图2,⊙O1和⊙O2相交于A、B两点,过点A作O1O2的平行线交两圆于C、D,已知O1O2=20cm,求CD的长。 ⌒⌒EF 例4 AB、BC是⊙O的弦,且AB⊥BC,M、N分别是AB、BC的中点,OM、ON分别交AB、BC于D、E,若OD=4cm,OE=3cm,求: (1)AB、BC的长;(2)⊙O的半径。⌒⌒ 1、已知⊙O中,弦AB、CD互相垂直,AB被CD分成的两条线段的长分别为5cm和13cm,则圆心O到CD的距离为________cm。 2、已知,⊙O中,AB=BC=OC分别交AC、BD于E、F,求证△OEF为等腰三角形。⌒⌒⌒ 例5、如图,在扇形OAB中,C是弧AB的中点,OC交AB于点D ,?AOC=30 0,AD=16cm求(1) ?OAB的度数(2)AB的长ABCDODO 练习:某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦长)为40米,拱高(弧的中点到弦的距离)为8米,求拱桥的半径。弦a、弦心距d、半径r、弓形高h之间的关系: 1、r=d+h 2、注意:要先将实际问题转化为数学问题 1、在⊙O中,M是AB的中点,N是弦AB的中点, AB=4 ,MN=2,求圆心到O到AB的距离。 2、如图所示,⊙O的直径AB和弦CD相交于E,AE=6cm,EB=14cm,∠DEB=300,求CD的长。 3、在Rt△ABC中,∠ACB=900,AC=8,BC=6,若以C为圆心,CB为半径的圆交AB于点P,求AP的长。 4、AB为⊙O的弦,P为AB上一点,AB=10,AP=4,OP=5,求⊙O的半径。
