20.1.1平均数(2) 课件(共39张PPT)
文档属性
| 名称 | 20.1.1平均数(2) 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 00:00:00 | ||
图片预览







文档简介
(共39张PPT)
20.1.1 平均数(2)
第2课时 用样本平均数估计总体平均数
人教版八年级下册
知识回顾
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则__________________叫做这n个数的加权平均数.
权
回顾平均数和加权平均数
2.在求一组数据的平均数时,某个数据出现的次数看作是这个数的______.
知识回顾
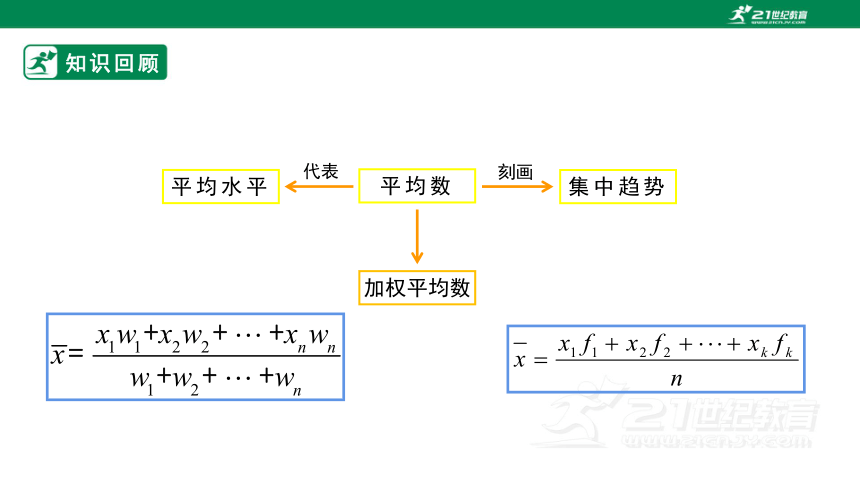
平均数
平均水平
代表
刻画
集中趋势
加权平均数
教学目标
1.理解怎样用样本平均数估计总体平均数.
2.会进行实际的计算.
新知导入
你能列举出生活中应用平均数的例子吗?
思考
新知探究
应用
汽车油耗
新知探究
App评分
应用
新知探究
应用
运动数
据统计
新知探究
应用
平均数应用
平均成绩
平均身高
人均年收入
平均体重
人均用水量
人均住房面积
人均GDP
新知探究
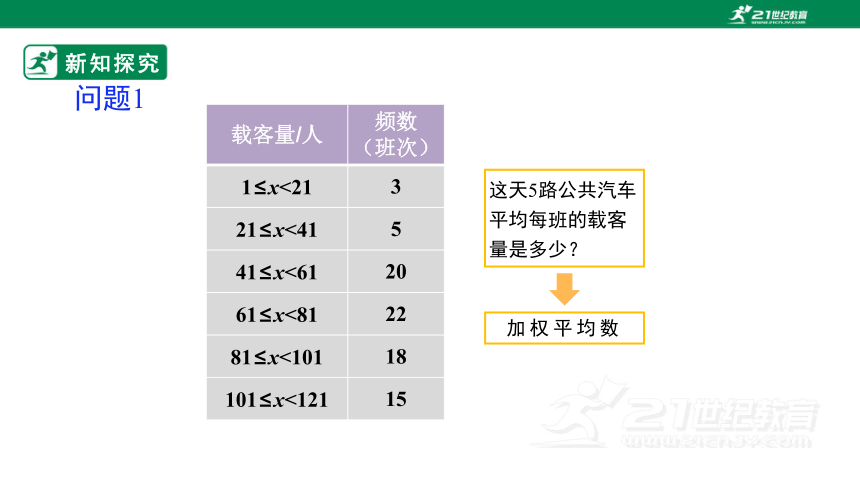
问题1
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表.这天5路公共汽车平均每班的载客量是多少(结果取整数)?
新知探究
问题1
加权平均数
这天5路公共汽车平均每班的载客量是多少?
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
新知探究
问题1
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
各组载客量
各组频数(权)
总频数
加权平均数
每组的载客量如何确定呢?
新知探究
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
组中值
数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数.
问题1
新知探究
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
61≤x<81 71 22
81≤x<101 91 18
101≤x<121 111 15
权
问题1
解:这天5路公共汽车平均每班的载客量是
= ≈ 73(人)
新知小结
频数分布表(图)中的加权平均数的求法:
①不同数据组中组中值的确定;
②权的确定.
组中值
实际数据
代表
频数
权
表示
计算
加权平均数
新知小结
权的形式
比例
百分比
重复次数
频数
新知练习
1.下表是校女子排球队队员的年龄分布.求校女子排球队队员的平均年龄(结果取整数).
解:
≈15(岁)
答:校女子排球队队员的平均年龄为15岁.
年龄/岁 13 14 15 16
频数 1 4 5 2
新知练习
2.为了绿化环境,柳荫街引进一批法国梧桐,三年后这些树的树干的周长情况如图所示,计算这批法国梧桐树干的平均周长(结果取整数).
答:这批法国梧桐树干的平均周长为64cm。
分析:先求出组中值
解:
新知探究
已知 A 村一果园中有 100 棵苹果树,在每年收获前果农会先估计一下当年的整体产量,那么应该采取什么样的方法进行估计呢?
新知探究
当所考察的对象很多,或者对考察对象带有破坏性时,我们该如何求取平均数?
在统计中我们常常通过用样本估计总体的方法来获得对总体的认识.因此,我们可以用样本的平均数来估计总体的平均数.
思考
(1)果农从100棵梨树中任意选出10棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
新知探究
样本具有代表性
解:==154
平均每棵苹果树上的苹果为 154 个.
新知探究
苹果的质量 0.2≤x<0.3 0.3≤x<0.4 0.4≤x<0.5 0.5≤x<0.6
频数 4 12 16 8
(2)为了进一步估计果园中苹果的总产量(单位:kg),果农从这 10 棵苹果树的每一棵树上分别随机摘取 4 个苹果,这些苹果的质量分布如下表:
新知探究
请你估计出这批苹果的平均质量.
解:==0.42
平均每个苹果的质量约为 0.42kg.
新知探究
每个梨的质量×梨的总个数
∴该果园中梨的总产量约为154×100×0.42=6468kg.
(3)能估计出该果园中梨的总产量吗?
新知小结
知识点:用样本平均数估计总体平均数
用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
新知小结
(1)一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也越精确,但相应的工作量也越大.因此在实际工作中,样本容量的确定既要考虑问题本身的需要,又要考虑实现的可能性及成本;
(2)抽取的样本要有随机性和代表性,这样有利于
估计总体,解决问题.
新知典例
例1 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命x/h 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200 2200≤x<2600
灯泡只数 5 10 12 17 6
分析:抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
新知探究
解:据上表得各小组的组中值,于是
∴可以估计这批灯泡的平均使用寿命大约是1672h.
即样本平均数为1672.
使用寿命x/h 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200 2200≤x<2600
灯泡只数 5 10 12 17 6
新知练习
1. 种菜能手李大叔种植了一批新品种黄瓜.为了考察这种黄瓜的生长情况,他随机抽查了部分黄瓜藤上长出的
黄瓜根数,得到下面的条形图.请估计这个新品种黄瓜平均每株结多少根黄瓜(结果取整数).
请估计这个新品种黄瓜平均每株结多少根黄瓜(结果取整数).
新知练习
解:
答:估计这个新品种黄瓜平均每株约结13根黄瓜.
新知练习
2. 八年级某班学生每天的睡眠时间情况如下(睡眠时间为x个小时):5≤x<6有1人,6≤x<7有3人,7≤x<8有4人,8≤x<9有40人,9≤x<10有2人.估计八年级学生平均睡眠时间为( )
A.6~7 h B.7~8 h
C.8~9 h D.9~10 h
C
课堂总结
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
课堂练习
1.某学校在开展“节约每一滴水”的活动中,从八年级的200名学生中任选出10名学生汇报了各自家庭一个月的节水情况,将有关数据整理如下表:
节水量/t 0.5 1 1.5 2
人数 2 3 4 1
请你估计这200名学生的家庭一个月节约用水的总量大约是( )
A.180 t B.200 t
C.240 t D.360 t
C
课堂练习
2.某校为了解该校八年级男生的身高,随机抽查了50 名该校八年级男生的身高,经统计得到下表,估计该校八年级男生的平均身高是多少.
身高/cm 组中值 频数(人数)
140≤x<150 145 6
150≤x<160 155 35
160≤x<170 165 7
170≤x<180 175 2
课堂练习
解析:由表中的组中值及加权平均数公式得
= =156(cm)
估计该校八年级男生的平均身高为 156cm.
课堂练习
3.为了建设“绿色县城”,A 县购进了一批香樟树,五年后这些树干的周长情况如下图所示,请你计算出这批香樟树树干的平均周长.
课堂练习
解:样本树干的平均周长是 = 63.8 cm.
则这批香樟树干的平均周长为 63.8 cm.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
20.1.1 平均数(2)
第2课时 用样本平均数估计总体平均数
人教版八年级下册
知识回顾
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则__________________叫做这n个数的加权平均数.
权
回顾平均数和加权平均数
2.在求一组数据的平均数时,某个数据出现的次数看作是这个数的______.
知识回顾
平均数
平均水平
代表
刻画
集中趋势
加权平均数
教学目标
1.理解怎样用样本平均数估计总体平均数.
2.会进行实际的计算.
新知导入
你能列举出生活中应用平均数的例子吗?
思考
新知探究
应用
汽车油耗
新知探究
App评分
应用
新知探究
应用
运动数
据统计
新知探究
应用
平均数应用
平均成绩
平均身高
人均年收入
平均体重
人均用水量
人均住房面积
人均GDP
新知探究
问题1
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表.这天5路公共汽车平均每班的载客量是多少(结果取整数)?
新知探究
问题1
加权平均数
这天5路公共汽车平均每班的载客量是多少?
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
新知探究
问题1
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
各组载客量
各组频数(权)
总频数
加权平均数
每组的载客量如何确定呢?
新知探究
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
组中值
数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数.
问题1
新知探究
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
61≤x<81 71 22
81≤x<101 91 18
101≤x<121 111 15
权
问题1
解:这天5路公共汽车平均每班的载客量是
= ≈ 73(人)
新知小结
频数分布表(图)中的加权平均数的求法:
①不同数据组中组中值的确定;
②权的确定.
组中值
实际数据
代表
频数
权
表示
计算
加权平均数
新知小结
权的形式
比例
百分比
重复次数
频数
新知练习
1.下表是校女子排球队队员的年龄分布.求校女子排球队队员的平均年龄(结果取整数).
解:
≈15(岁)
答:校女子排球队队员的平均年龄为15岁.
年龄/岁 13 14 15 16
频数 1 4 5 2
新知练习
2.为了绿化环境,柳荫街引进一批法国梧桐,三年后这些树的树干的周长情况如图所示,计算这批法国梧桐树干的平均周长(结果取整数).
答:这批法国梧桐树干的平均周长为64cm。
分析:先求出组中值
解:
新知探究
已知 A 村一果园中有 100 棵苹果树,在每年收获前果农会先估计一下当年的整体产量,那么应该采取什么样的方法进行估计呢?
新知探究
当所考察的对象很多,或者对考察对象带有破坏性时,我们该如何求取平均数?
在统计中我们常常通过用样本估计总体的方法来获得对总体的认识.因此,我们可以用样本的平均数来估计总体的平均数.
思考
(1)果农从100棵梨树中任意选出10棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
新知探究
样本具有代表性
解:==154
平均每棵苹果树上的苹果为 154 个.
新知探究
苹果的质量 0.2≤x<0.3 0.3≤x<0.4 0.4≤x<0.5 0.5≤x<0.6
频数 4 12 16 8
(2)为了进一步估计果园中苹果的总产量(单位:kg),果农从这 10 棵苹果树的每一棵树上分别随机摘取 4 个苹果,这些苹果的质量分布如下表:
新知探究
请你估计出这批苹果的平均质量.
解:==0.42
平均每个苹果的质量约为 0.42kg.
新知探究
每个梨的质量×梨的总个数
∴该果园中梨的总产量约为154×100×0.42=6468kg.
(3)能估计出该果园中梨的总产量吗?
新知小结
知识点:用样本平均数估计总体平均数
用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
新知小结
(1)一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也越精确,但相应的工作量也越大.因此在实际工作中,样本容量的确定既要考虑问题本身的需要,又要考虑实现的可能性及成本;
(2)抽取的样本要有随机性和代表性,这样有利于
估计总体,解决问题.
新知典例
例1 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命x/h 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200 2200≤x<2600
灯泡只数 5 10 12 17 6
分析:抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
新知探究
解:据上表得各小组的组中值,于是
∴可以估计这批灯泡的平均使用寿命大约是1672h.
即样本平均数为1672.
使用寿命x/h 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200 2200≤x<2600
灯泡只数 5 10 12 17 6
新知练习
1. 种菜能手李大叔种植了一批新品种黄瓜.为了考察这种黄瓜的生长情况,他随机抽查了部分黄瓜藤上长出的
黄瓜根数,得到下面的条形图.请估计这个新品种黄瓜平均每株结多少根黄瓜(结果取整数).
请估计这个新品种黄瓜平均每株结多少根黄瓜(结果取整数).
新知练习
解:
答:估计这个新品种黄瓜平均每株约结13根黄瓜.
新知练习
2. 八年级某班学生每天的睡眠时间情况如下(睡眠时间为x个小时):5≤x<6有1人,6≤x<7有3人,7≤x<8有4人,8≤x<9有40人,9≤x<10有2人.估计八年级学生平均睡眠时间为( )
A.6~7 h B.7~8 h
C.8~9 h D.9~10 h
C
课堂总结
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
课堂练习
1.某学校在开展“节约每一滴水”的活动中,从八年级的200名学生中任选出10名学生汇报了各自家庭一个月的节水情况,将有关数据整理如下表:
节水量/t 0.5 1 1.5 2
人数 2 3 4 1
请你估计这200名学生的家庭一个月节约用水的总量大约是( )
A.180 t B.200 t
C.240 t D.360 t
C
课堂练习
2.某校为了解该校八年级男生的身高,随机抽查了50 名该校八年级男生的身高,经统计得到下表,估计该校八年级男生的平均身高是多少.
身高/cm 组中值 频数(人数)
140≤x<150 145 6
150≤x<160 155 35
160≤x<170 165 7
170≤x<180 175 2
课堂练习
解析:由表中的组中值及加权平均数公式得
= =156(cm)
估计该校八年级男生的平均身高为 156cm.
课堂练习
3.为了建设“绿色县城”,A 县购进了一批香樟树,五年后这些树干的周长情况如下图所示,请你计算出这批香樟树树干的平均周长.
课堂练习
解:样本树干的平均周长是 = 63.8 cm.
则这批香樟树干的平均周长为 63.8 cm.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
