第五章 回顾与思考[上学期]

课件16张PPT。复习目标：
1 会把实际问题建立反比例函数，了解反比例函数的概念，
2 能画出反比例的图形，根据图象和解析式探索并理解反比例函数的主要性质。
3 提高观察和归纳分析能力，体验数形结合的数学思想方法。
4 能依据已知条件确定反比例函数。
教学方法：探索法，归纳法，多媒体教学辅助
教学重点；反比例函数的概念，图象和性质及建立数学模型的能力驶向胜利的彼岸温故而知新反比例函数的图象和性质
形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;
增减性 反比例函数的图象,当k>0时,在每一象限内,y随x的增大而减小; 当k<0时,在每一象限内,y随x的增大而增大.
图象的发展趋势 反比例函数的图象无限接近于x,y轴,但永远达不到x,y轴,画图象时,要体现出这个特点.
对称性 反比例函数的图象是关于原点成中心对称的图形.
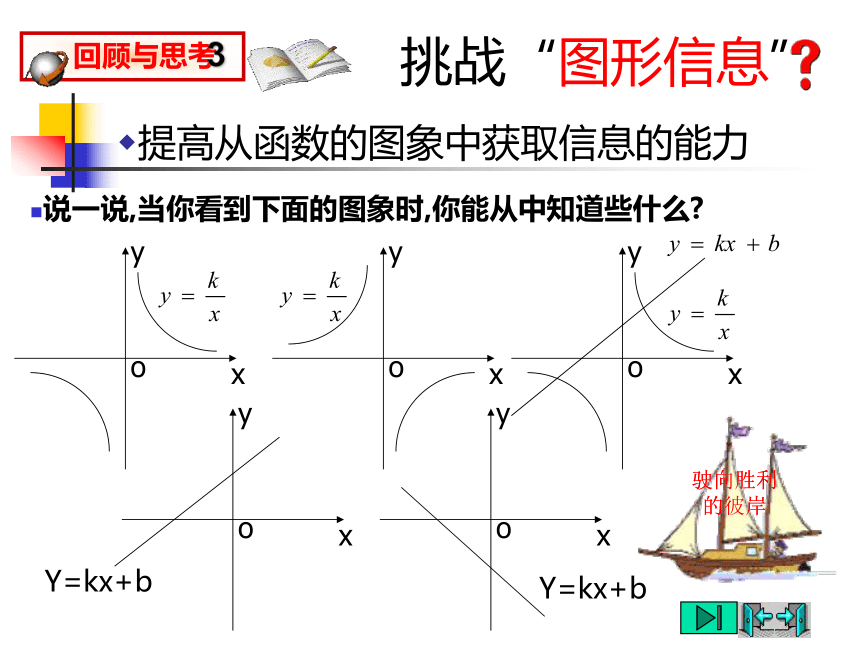
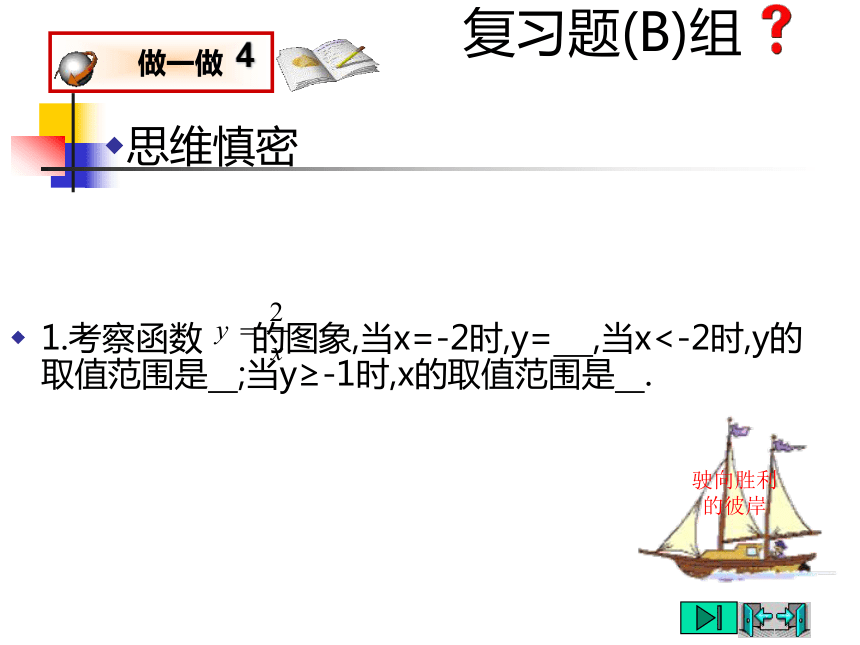
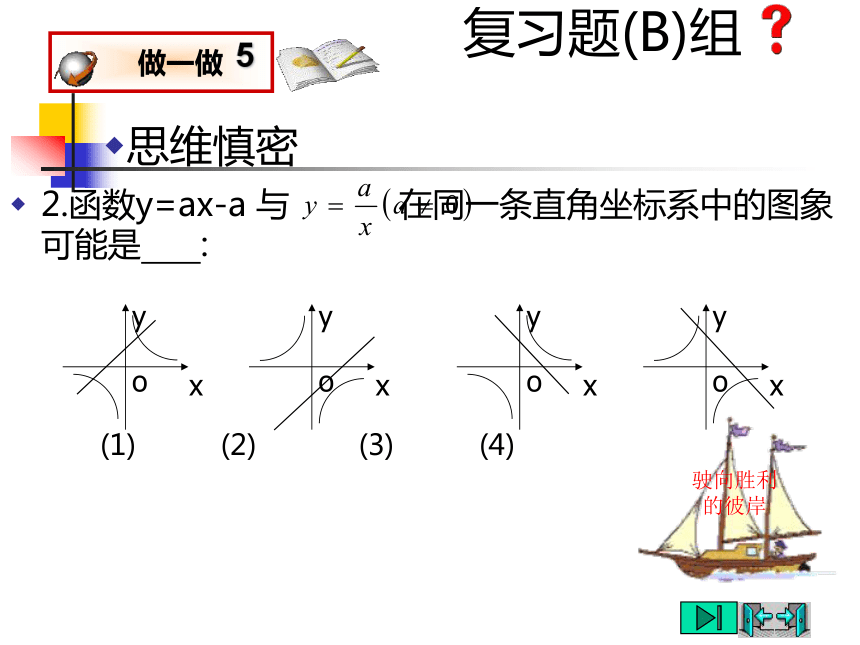
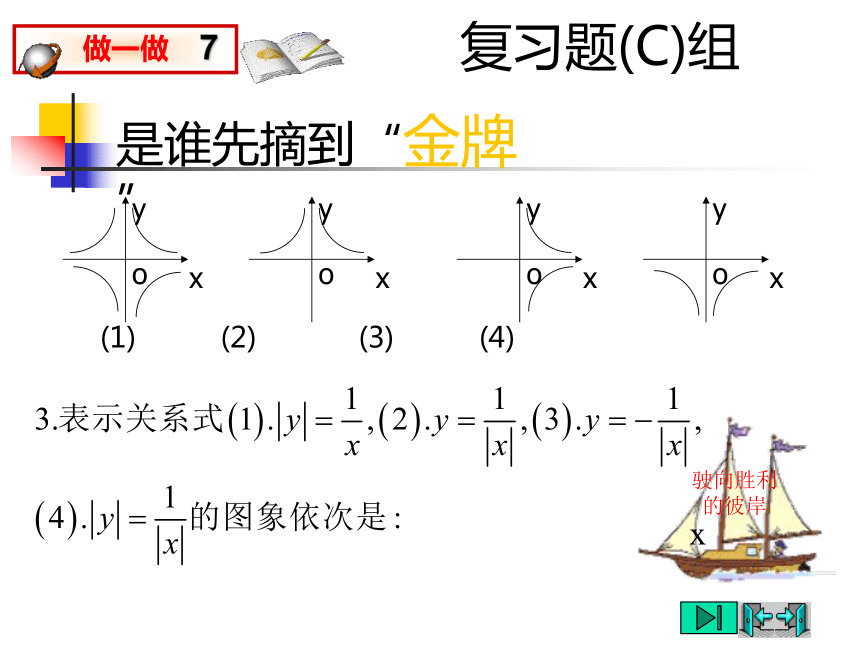
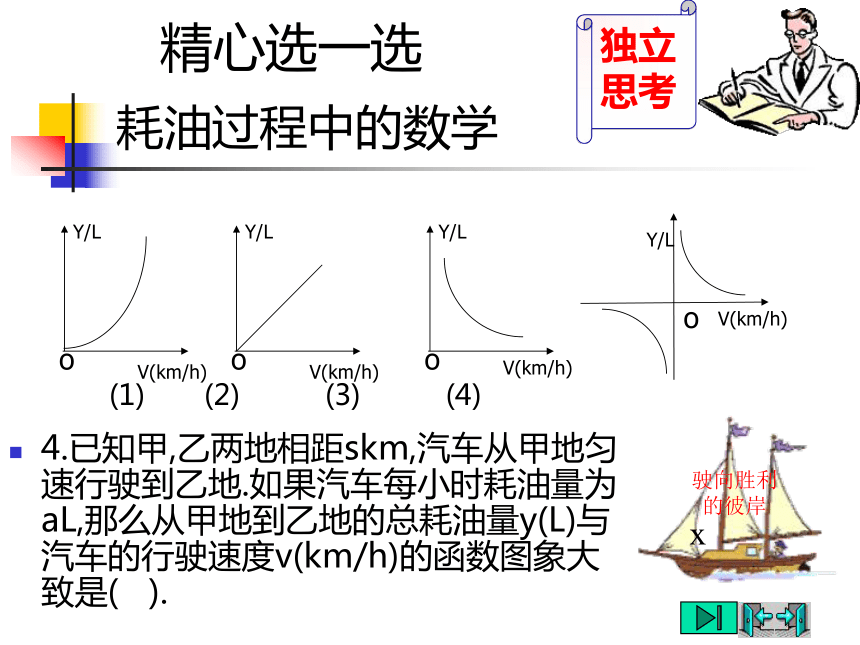
任意一组变量的乘积是一个定值,即xy=k.反比例函数挑战“图形信息”提高从函数的图象中获取信息的能力驶向胜利的彼岸驶向胜利的彼岸说一说,当你看到下面的图象时,你能从中知道些什么?复习题(B)组1.考察函数 的图象,当x=-2时,y= ,当x<-2时,y的取值范围是 ;当y≥-1时,x的取值范围是 .思维慎密驶向胜利的彼岸复习题(B)组2.函数y=ax-a 与 在同一条直角坐标系中的图象可能是 :思维慎密驶向胜利的彼岸复习题(C)组驶向胜利的彼岸x是谁先摘到“金牌”精心选一选4.已知甲,乙两地相距skm,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为aL,那么从甲地到乙地的总耗油量y(L)与汽车的行驶速度v(km/h)的函数图象大致是( ).驶向胜利的彼岸x耗油过程中的数学请“图象”帮忙人均产量中的数学5.某村的粮食总产量为a(a为常数),设该村粮食的人均产量为y(吨),人口数为x(人),则y与x之间的函数图象大致是( ).驶向胜利的彼岸面积计算中的函数知识方法结“网络”6.已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).驶向胜利的彼岸“试金石” 牵一发而动全身驶向胜利的彼岸 练 习 1⑴ 写出下列函数关系式，并指出它们是什么函数?
ⅰ当路程 s 一定时，时间 t 与速度 v 的函数关系
ⅱ当矩形面积 S一定时，长 a 与宽 b 的函数关系
ⅲ当三角形面积 S 一定时，三角形的底边 y 与高 x
的函数关系
⑵ 在下列函数中，y是x的反比例函数的是（ ）
（A） （B） + 7
（C）xy = 5 （D）
⑶ 已知函数 是正比例函数,则 m = ___ ；

已知函数 是反比例函数,则 m = ___ 。 练 习 1C86二,四减小m < 2三3增大
练 习 31. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )2. 已知k>0,则函数 y1=kx与y2= 在同一坐标系中
的图象大致是 ( )3.设x为一切实数，在下列函数中，当x减小时，y的值总是增大的函数是( )(A) y = -5x -1 ( B)y = (C)y=-2x+2； (D)y=4x.DCC①已知y 与 x 成反比例, 并且当 x = 3, y = 7时，求 x 与 y 的函数关系式。 ③已知y 与 x2 成反比例, 并且当 x = 3时
y = 4，求 x = 1.5 时 y的值。练习4②根据图形写出函数的解析式。 已知y与x2成反比例，当x=3时y=4求x=1.5时y的值
解：设x2y=k,因为 x=3时y=4，所以9×4= k,所以 k=36 ，当x=1.5时,y=36 ÷1.5=24①如果y与z成正比例, z 与x成正比例,则 y 与x 的函数关系是： ③如果y与z成反比例, z 与x成正比例,则 y 与x 的函数关系是： 练 习5②如果y与z成正比例, z 与x成反比例,则 y 与x 的函数关系是： ④如果y与z成反比例, z 与x成反比例,则 y 与x 的函数关系是： Y与x成正比例Y与x成反比例Y与x成反比例Y与x成正比例