数学人教A版(2019)必修第一册2.2基本不等式 课件(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册2.2基本不等式 课件(共23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 17:26:54 | ||
图片预览








文档简介
(共23张PPT)
基本不等式
基本不等式:
一、情境创设 导入课题
情境1:你见过这个图形吗?
第24届国际数学家大会(ICM2002)的会标
会标的设计源自中国古代数学家赵爽为了证明发明于中国周代的勾股定理而绘制的弦图。它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学精英们。
(3) =
(2) =
(1)正方形 的边长为
问题 :对于“情境2”中的图形,把“风车”抽象成平面图形.在正方形
中有4个全等的直角三角形.设直角三角形的两条直角边长为 ,
正方形 的面积为 ,4个直角三角形的面积和为 ,则
(4)由图可知, ,即:
一、情境创设 导入课题
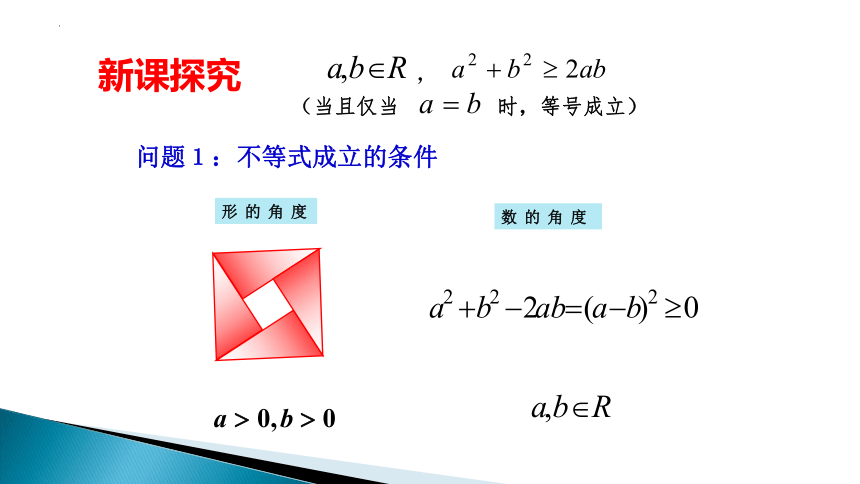
问题1:不等式成立的条件
形 的 角 度
数 的 角 度
(当且仅当 时,等号成立)
,
新课探究
一般地,对于任意实数 ,我们有
当且仅当 时等号成立
重要不等式:
新课探究
问题2:
特别地,当a≥0,b≥0时,在不等式中,以 、 分别代替a、b,得到什么?
1. 对于任意实数a,b,总有
当且仅当a=b时,等号成立.
2. 如果a,b都是非负实数,那么
当且仅当a=b时,等号成立.
我们称上述不等式为基本不等式,其中 称为a,b的算术
平均数, 称为a,b几何平均数. 因此,基本不等式又被称为
均值不等式.
探究结果
●
●
●
●
●
●
●
●
1. 对于任意实数a,b,总有
当且仅当a=b时,等号成立.
2. 如果a,b都是非负实数,那么
当且仅当a=b时,等号成立.
探究结果
证明(作差法)
当且仅当a=b时,等号成立.
基本不等式:
几何平均数
算术平均数
文字叙述:(1)两个非负数数算术平均数不小于它们的几何平均数
(2)两个正数的等差中项不小于它们的等比中项.
几何意义:?
基本不等式的几何解释
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
③OD与CD的大小关系怎样 OD_____CD
≥
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
几何意义:半径不小于弦长的一半
A
D
B
E
O
C
a
b
问题三:
基本不等式:
几何意义:半径不小于弦长的一半
文字叙述:(1)两个非负数的算术平均数不小于它们的几何平均数
(2)两个正数的等差中项不小于它们的等比中项.
基本不等式:
当且仅当a =b时,等号成立.
当且仅当a=b时,等号成立.
重要不等式:
注意:
(1)不同点:两个不等式的适用范围不同。
(2)相同点:当且仅当a=b时,等号成立。
例题讲解
证明 (方法1) 因a,b均为正数,由基本不等式可得
当且仅当 时,等号成立.
例1
例题讲解
当且仅当a=b时,等号成立.
证明 (方法2)
例1
几何解释
思考交流
课堂升华
F
B
O
C
D
B
A
O
C
a
b
C'
①
②
③
④
①
②
③
④
课堂训练
证明 由a,b,c>0得
同向相加可得
练习
例题讲解
解 因为a,b,c,d>0,
练习
小结:
两个重要的不等式
基本不等式
基本不等式:
一、情境创设 导入课题
情境1:你见过这个图形吗?
第24届国际数学家大会(ICM2002)的会标
会标的设计源自中国古代数学家赵爽为了证明发明于中国周代的勾股定理而绘制的弦图。它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学精英们。
(3) =
(2) =
(1)正方形 的边长为
问题 :对于“情境2”中的图形,把“风车”抽象成平面图形.在正方形
中有4个全等的直角三角形.设直角三角形的两条直角边长为 ,
正方形 的面积为 ,4个直角三角形的面积和为 ,则
(4)由图可知, ,即:
一、情境创设 导入课题
问题1:不等式成立的条件
形 的 角 度
数 的 角 度
(当且仅当 时,等号成立)
,
新课探究
一般地,对于任意实数 ,我们有
当且仅当 时等号成立
重要不等式:
新课探究
问题2:
特别地,当a≥0,b≥0时,在不等式中,以 、 分别代替a、b,得到什么?
1. 对于任意实数a,b,总有
当且仅当a=b时,等号成立.
2. 如果a,b都是非负实数,那么
当且仅当a=b时,等号成立.
我们称上述不等式为基本不等式,其中 称为a,b的算术
平均数, 称为a,b几何平均数. 因此,基本不等式又被称为
均值不等式.
探究结果
●
●
●
●
●
●
●
●
1. 对于任意实数a,b,总有
当且仅当a=b时,等号成立.
2. 如果a,b都是非负实数,那么
当且仅当a=b时,等号成立.
探究结果
证明(作差法)
当且仅当a=b时,等号成立.
基本不等式:
几何平均数
算术平均数
文字叙述:(1)两个非负数数算术平均数不小于它们的几何平均数
(2)两个正数的等差中项不小于它们的等比中项.
几何意义:?
基本不等式的几何解释
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
③OD与CD的大小关系怎样 OD_____CD
≥
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
几何意义:半径不小于弦长的一半
A
D
B
E
O
C
a
b
问题三:
基本不等式:
几何意义:半径不小于弦长的一半
文字叙述:(1)两个非负数的算术平均数不小于它们的几何平均数
(2)两个正数的等差中项不小于它们的等比中项.
基本不等式:
当且仅当a =b时,等号成立.
当且仅当a=b时,等号成立.
重要不等式:
注意:
(1)不同点:两个不等式的适用范围不同。
(2)相同点:当且仅当a=b时,等号成立。
例题讲解
证明 (方法1) 因a,b均为正数,由基本不等式可得
当且仅当 时,等号成立.
例1
例题讲解
当且仅当a=b时,等号成立.
证明 (方法2)
例1
几何解释
思考交流
课堂升华
F
B
O
C
D
B
A
O
C
a
b
C'
①
②
③
④
①
②
③
④
课堂训练
证明 由a,b,c>0得
同向相加可得
练习
例题讲解
解 因为a,b,c,d>0,
练习
小结:
两个重要的不等式
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
