4.1光的折射课件(共32张ppt)人教版(2019)选择性必修第一册第四章 光
文档属性
| 名称 | 4.1光的折射课件(共32张ppt)人教版(2019)选择性必修第一册第四章 光 |  | |
| 格式 | pptx | ||
| 文件大小 | 147.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-15 17:53:16 | ||
图片预览







文档简介
(共32张PPT)
高二物理(人教版2019)
4.1 光的折射
射水鱼在水中能准确射中水面上不远处的小昆虫。水中的鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?
铅笔折断了吗?
海市蜃楼是怎么形成的?
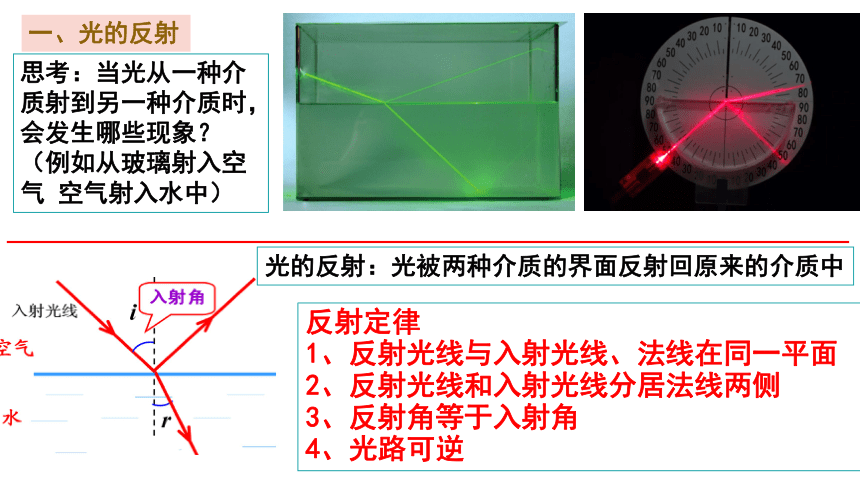
思考:当光从一种介质射到另一种介质时,会发生哪些现象?
(例如从玻璃射入空气 空气射入水中)
一、光的反射
光的反射:光被两种介质的界面反射回原来的介质中
反射定律
1、反射光线与入射光线、法线在同一平面
2、反射光线和入射光线分居法线两侧
3、反射角等于入射角
4、光路可逆
入射光线
反射光线
法线
入射角
反射角
折射光线
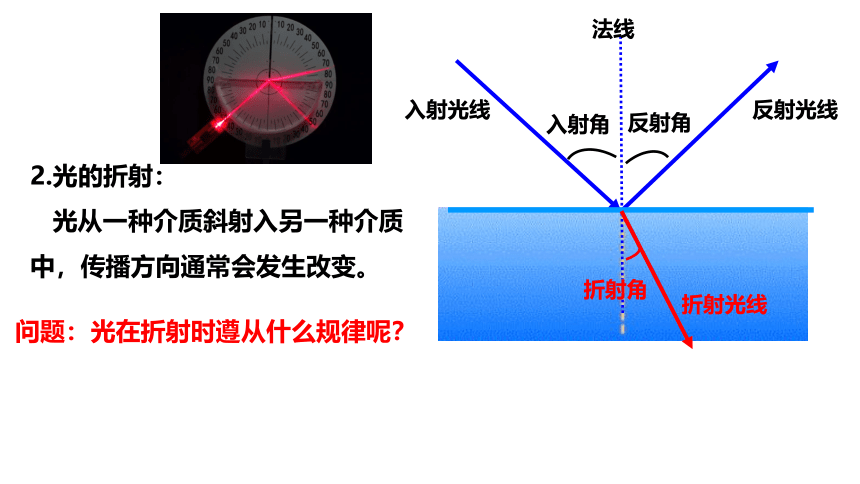
2.光的折射:
光从一种介质斜射入另一种介质中,传播方向通常会发生改变。
折射角
问题:光在折射时遵从什么规律呢?
(1)实验现象:
1.折射光线、入射光线、法线在同一平面内;
2.折射光线和入射光线分居法线两侧;
3.当光从空气斜射入玻璃中时,折射角小于入射角;
4.当光从玻璃斜射入空气中时,折射角大于入射角;
5.当入射角增大时,折射角也随着增大 ;
6.光路可逆;
7.当光垂直界面入射时,传播方向不变。
思考:入射角与折射角有什么定量关系呢?
(空气中的角最大)
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
=n(n为常数)
以光从空气射入玻璃为例
思考:如果将玻璃换成其它介质,入射角和折射角的正弦之比是否还是常数?这个常数是否变化?
二、光的折射
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
斯涅耳
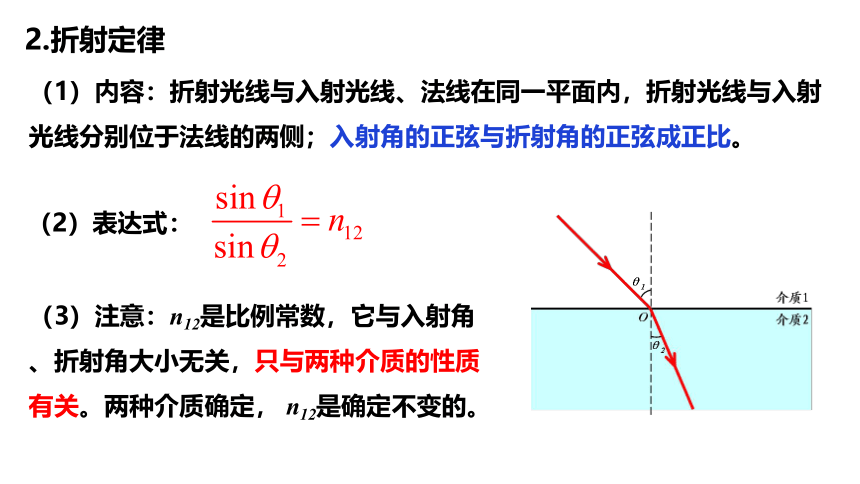
2.折射定律
(1)内容:折射光线与入射光线、法线在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比。
(2)表达式:
(3)注意:n12是比例常数,它与入射角、折射角大小无关,只与两种介质的性质有关。两种介质确定, n12是确定不变的。
二、折射率
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。
2.公式:
或
思考:光从真空进入某种介质,哪些物理量发生了变化?
——折射率的定义式
——折射率的决定式
波速发生变化
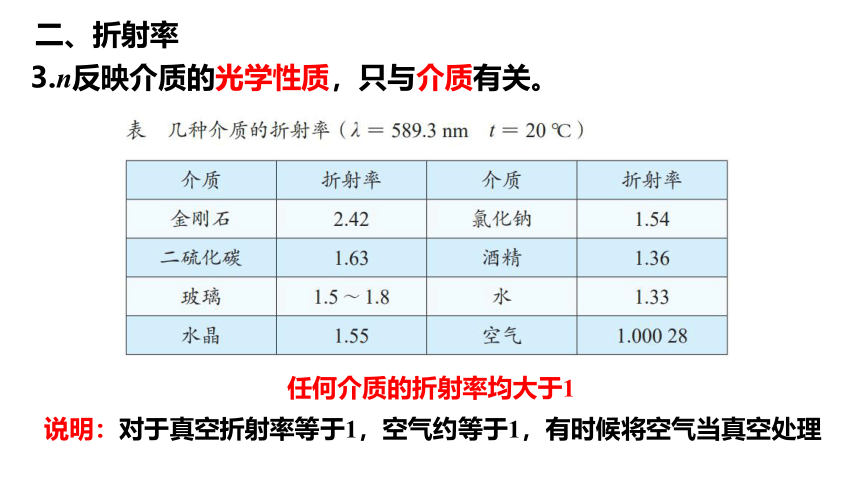
3.n反映介质的光学性质,只与介质有关。
任何介质的折射率均大于1
二、折射率
说明:对于真空折射率等于1,空气约等于1,有时候将空气当真空处理
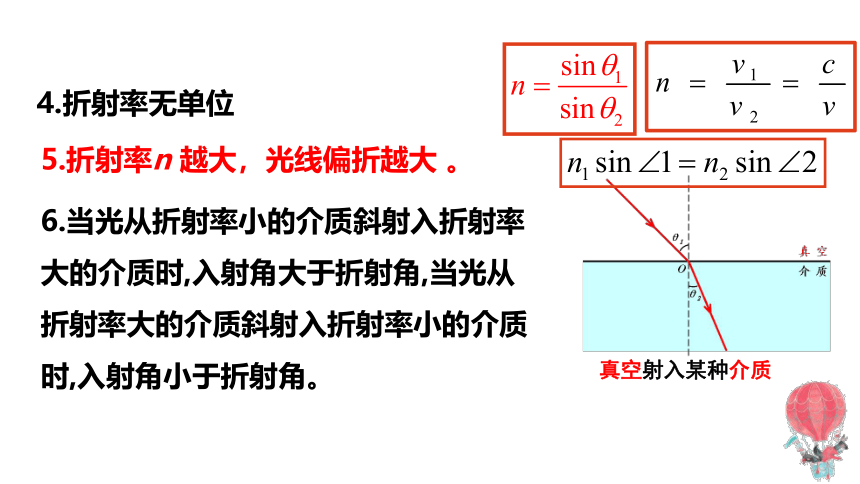
4.折射率无单位
5.折射率n 越大,光线偏折越大 。
6.当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
真空射入某种介质
真空中速度 真空中频率 真空中波长 同种介质中速度 同种介质中频率 同种介质中波长 折射率 临界角
红光 c 小 大 大 小 大 小 大
紫光 c 大 小 小 大 小 大 小
可见光光谱:红、橙、黄、绿、蓝、靛、紫(频率升高、真空波长变短)
【例题】如图一个储油桶的底面直径与高均为d.当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶底上的点C,CB两点距离d/4.求油的折射率和光在油中传播的速度。
B
A
d
C
O
D
N
Nˊ
θ2
新课讲授
解:
折射率问题的分析方法
解决此类光路问题,关键是辨清“三线、两角、一界面”间的关系。注意以下几点:
(1)根据题意正确画出光路图。
(2)利用几何关系确定光路中的边、角关系,注意入射角、折射角的确定。
(3)利用折射定律、几何关系、三角函数求解。
(4)注意光路的可逆性的利用。
S
S′
有大气,看到太阳更早。没有大气,将迟一些看到太阳。
蒙气差现象
为什么铅笔好像折了一样?
(5)视深问题
空气
水
A
A
眼神不拐弯
由于光的折射,水中物体的位置看起来比实际位置要高些。
井中的水下青蛙看岸上的物体的位置偏向哪里?
上方
井中的水下青蛙看井口的宽度是偏大还是偏小?
偏小
坐井观天 所见甚小
有水乃大
有水的青蛙和枯井的青蛙,哪个视线范围大?
有水
课堂练习
例1:图是光线由空气射入半圆形玻璃砖,再由玻璃砖射入空气中的光路图。O点是半圆形玻璃砖的圆心,指出哪些情况是可能发生的,哪些情况是不可能发生的。
解:甲、丁不可能发生,乙、丙可能发生。
例2:图是光由空气射入某种介质时的折射情况,试由图中所给出的数据求出这种介质的折射率和这种介质中的光速。
课堂练习
解:
如何把玻璃的折射率测出来?
玻璃是一种透明介质,光从空气入射到玻璃的界面上会发生折射,如何把玻璃的折射率测出来?
新课讲授
三、实验:测量玻璃的折射率
一、实验目的
掌握测量玻璃折射率的方法。
二、实验设计
1.实验方案
如图当光以一定的入射角透过一块两面平行的玻璃砖时,只要找出与入射光线AO相对应的出射光线O′D就能够画出光从空气射入玻璃后的折射光线OO′,于是就能测量入射角θ1、折射角θ2。根据折射定律,就可以求出玻璃的折射率了。
新课讲授
新课讲授
三、实验步骤
1.如图所示,将白纸用图钉钉在平木板上。
2.在白纸上画出一条直线aa′作为界面(线)。过aa′上的一点O画出界面的法线NN′,并画一条线段AO作为入射光线。
3.把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′。
4.在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像。再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置。
5.移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向。
6.连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角,从三角函数表中查出它们的正弦值,把这些数据记录在自己设计的表格中。
新课讲授
三、实验步骤
新课讲授
新课讲授
测量玻璃的折射率
1.图象法:
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
四、数据处理
2.单位圆法:在不使用量角器的情况下,可以用单位圆法。
①以入射点O为圆心,以一定长度R为半径画圆,交入射光线OA于E点,交折射光线OO′于E′点,过E作NN′的垂线EH,过E′作NN′的垂线E′H′。如图所示。
②由图中关系sinθ1=,sinθ2= ,OE=OE′=R,则n==。只要用刻度尺测出EH、E′H′的长度就可以求出n。
四、数据处理
五、实验误差
1.确定入射光线、出射光线时会造成误差,故确定光线方位时所插两枚大头针的间距应大一些,玻璃砖应宽一些。
2.入射角、折射角测量的不精确。为减小测角时的相对误差,入射角要稍大些,但不宜太大,入射角太大时,反射光较强,折射光会相对较弱。
六、注意事项
1.实验中,玻璃砖在纸上的位置不可移动。
2.不能用手触摸玻璃砖光洁的光学面,更不能把玻璃砖当尺子用。
3.大头针应竖直插在白纸上,且玻璃砖每一侧两枚大头针P1与P2间、P3与P4间的距离应大些,以减小确定光路方向时造成的误差。
4.实验中入射角不宜过小,否则会使测量误差较大;也不宜过大,否则在bb′一侧的光线偏向玻璃砖侧边缘,不易观察到P1、P2的像。
5.玻璃砖应选用宽度较大的,最好在5 cm以上,若玻璃砖的宽度太小,则测量误差较大。
例3 (多选)某同学用“插针法”做测定玻璃折射率实验时,他的方法和操作步骤都正确无误,但他处理实验数据时,发现玻璃砖的两个光学面aa′和bb′不平行,如图,则( )
A.P1P2与P3P4两条直线平行
B.P1P2与P3P4两条直线不平行
C.他测出的折射率偏大
D.他测出的折射率不受影响
高二物理(人教版2019)
4.1 光的折射
射水鱼在水中能准确射中水面上不远处的小昆虫。水中的鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?
铅笔折断了吗?
海市蜃楼是怎么形成的?
思考:当光从一种介质射到另一种介质时,会发生哪些现象?
(例如从玻璃射入空气 空气射入水中)
一、光的反射
光的反射:光被两种介质的界面反射回原来的介质中
反射定律
1、反射光线与入射光线、法线在同一平面
2、反射光线和入射光线分居法线两侧
3、反射角等于入射角
4、光路可逆
入射光线
反射光线
法线
入射角
反射角
折射光线
2.光的折射:
光从一种介质斜射入另一种介质中,传播方向通常会发生改变。
折射角
问题:光在折射时遵从什么规律呢?
(1)实验现象:
1.折射光线、入射光线、法线在同一平面内;
2.折射光线和入射光线分居法线两侧;
3.当光从空气斜射入玻璃中时,折射角小于入射角;
4.当光从玻璃斜射入空气中时,折射角大于入射角;
5.当入射角增大时,折射角也随着增大 ;
6.光路可逆;
7.当光垂直界面入射时,传播方向不变。
思考:入射角与折射角有什么定量关系呢?
(空气中的角最大)
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
=n(n为常数)
以光从空气射入玻璃为例
思考:如果将玻璃换成其它介质,入射角和折射角的正弦之比是否还是常数?这个常数是否变化?
二、光的折射
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
斯涅耳
2.折射定律
(1)内容:折射光线与入射光线、法线在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比。
(2)表达式:
(3)注意:n12是比例常数,它与入射角、折射角大小无关,只与两种介质的性质有关。两种介质确定, n12是确定不变的。
二、折射率
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。
2.公式:
或
思考:光从真空进入某种介质,哪些物理量发生了变化?
——折射率的定义式
——折射率的决定式
波速发生变化
3.n反映介质的光学性质,只与介质有关。
任何介质的折射率均大于1
二、折射率
说明:对于真空折射率等于1,空气约等于1,有时候将空气当真空处理
4.折射率无单位
5.折射率n 越大,光线偏折越大 。
6.当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
真空射入某种介质
真空中速度 真空中频率 真空中波长 同种介质中速度 同种介质中频率 同种介质中波长 折射率 临界角
红光 c 小 大 大 小 大 小 大
紫光 c 大 小 小 大 小 大 小
可见光光谱:红、橙、黄、绿、蓝、靛、紫(频率升高、真空波长变短)
【例题】如图一个储油桶的底面直径与高均为d.当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶底上的点C,CB两点距离d/4.求油的折射率和光在油中传播的速度。
B
A
d
C
O
D
N
Nˊ
θ2
新课讲授
解:
折射率问题的分析方法
解决此类光路问题,关键是辨清“三线、两角、一界面”间的关系。注意以下几点:
(1)根据题意正确画出光路图。
(2)利用几何关系确定光路中的边、角关系,注意入射角、折射角的确定。
(3)利用折射定律、几何关系、三角函数求解。
(4)注意光路的可逆性的利用。
S
S′
有大气,看到太阳更早。没有大气,将迟一些看到太阳。
蒙气差现象
为什么铅笔好像折了一样?
(5)视深问题
空气
水
A
A
眼神不拐弯
由于光的折射,水中物体的位置看起来比实际位置要高些。
井中的水下青蛙看岸上的物体的位置偏向哪里?
上方
井中的水下青蛙看井口的宽度是偏大还是偏小?
偏小
坐井观天 所见甚小
有水乃大
有水的青蛙和枯井的青蛙,哪个视线范围大?
有水
课堂练习
例1:图是光线由空气射入半圆形玻璃砖,再由玻璃砖射入空气中的光路图。O点是半圆形玻璃砖的圆心,指出哪些情况是可能发生的,哪些情况是不可能发生的。
解:甲、丁不可能发生,乙、丙可能发生。
例2:图是光由空气射入某种介质时的折射情况,试由图中所给出的数据求出这种介质的折射率和这种介质中的光速。
课堂练习
解:
如何把玻璃的折射率测出来?
玻璃是一种透明介质,光从空气入射到玻璃的界面上会发生折射,如何把玻璃的折射率测出来?
新课讲授
三、实验:测量玻璃的折射率
一、实验目的
掌握测量玻璃折射率的方法。
二、实验设计
1.实验方案
如图当光以一定的入射角透过一块两面平行的玻璃砖时,只要找出与入射光线AO相对应的出射光线O′D就能够画出光从空气射入玻璃后的折射光线OO′,于是就能测量入射角θ1、折射角θ2。根据折射定律,就可以求出玻璃的折射率了。
新课讲授
新课讲授
三、实验步骤
1.如图所示,将白纸用图钉钉在平木板上。
2.在白纸上画出一条直线aa′作为界面(线)。过aa′上的一点O画出界面的法线NN′,并画一条线段AO作为入射光线。
3.把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′。
4.在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像。再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置。
5.移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向。
6.连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角,从三角函数表中查出它们的正弦值,把这些数据记录在自己设计的表格中。
新课讲授
三、实验步骤
新课讲授
新课讲授
测量玻璃的折射率
1.图象法:
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
四、数据处理
2.单位圆法:在不使用量角器的情况下,可以用单位圆法。
①以入射点O为圆心,以一定长度R为半径画圆,交入射光线OA于E点,交折射光线OO′于E′点,过E作NN′的垂线EH,过E′作NN′的垂线E′H′。如图所示。
②由图中关系sinθ1=,sinθ2= ,OE=OE′=R,则n==。只要用刻度尺测出EH、E′H′的长度就可以求出n。
四、数据处理
五、实验误差
1.确定入射光线、出射光线时会造成误差,故确定光线方位时所插两枚大头针的间距应大一些,玻璃砖应宽一些。
2.入射角、折射角测量的不精确。为减小测角时的相对误差,入射角要稍大些,但不宜太大,入射角太大时,反射光较强,折射光会相对较弱。
六、注意事项
1.实验中,玻璃砖在纸上的位置不可移动。
2.不能用手触摸玻璃砖光洁的光学面,更不能把玻璃砖当尺子用。
3.大头针应竖直插在白纸上,且玻璃砖每一侧两枚大头针P1与P2间、P3与P4间的距离应大些,以减小确定光路方向时造成的误差。
4.实验中入射角不宜过小,否则会使测量误差较大;也不宜过大,否则在bb′一侧的光线偏向玻璃砖侧边缘,不易观察到P1、P2的像。
5.玻璃砖应选用宽度较大的,最好在5 cm以上,若玻璃砖的宽度太小,则测量误差较大。
例3 (多选)某同学用“插针法”做测定玻璃折射率实验时,他的方法和操作步骤都正确无误,但他处理实验数据时,发现玻璃砖的两个光学面aa′和bb′不平行,如图,则( )
A.P1P2与P3P4两条直线平行
B.P1P2与P3P4两条直线不平行
C.他测出的折射率偏大
D.他测出的折射率不受影响
