2023春人教版六年级数学下册 圆柱的体积(第2课时)(课件)(共25张PPT)
文档属性
| 名称 | 2023春人教版六年级数学下册 圆柱的体积(第2课时)(课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 07:27:42 | ||
图片预览



文档简介
(共25张PPT)
圆柱的体积(第2课时)
转化
小丽
长方体的底面积等于圆柱的底面积,
圆柱的体积=底面积×高
未知
转化
已知
V = Sh = πr h
长方体的高等于圆柱的高。
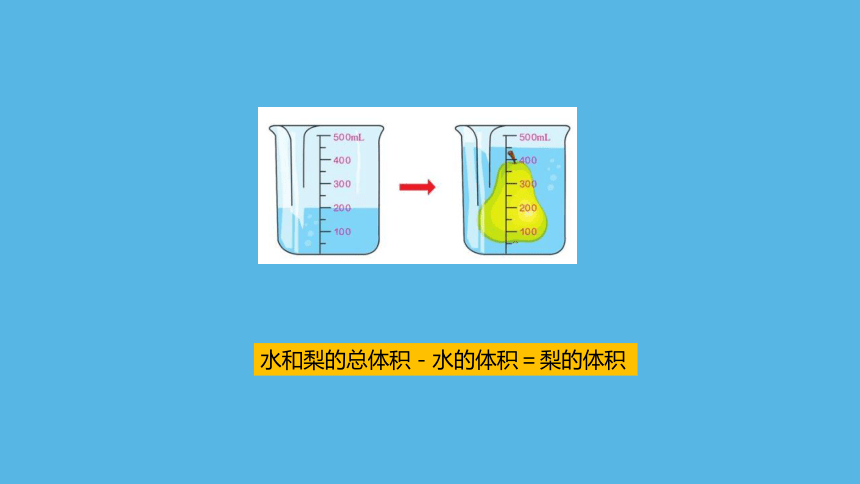
水和梨的总体积-水的体积=梨的体积
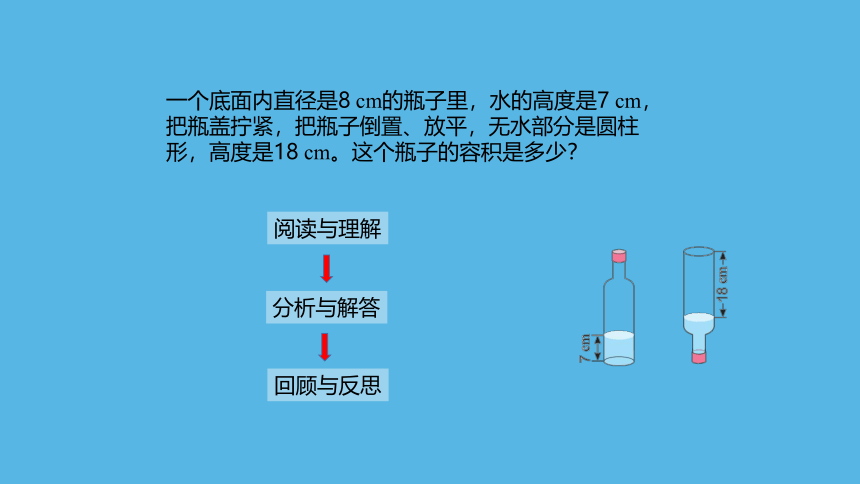
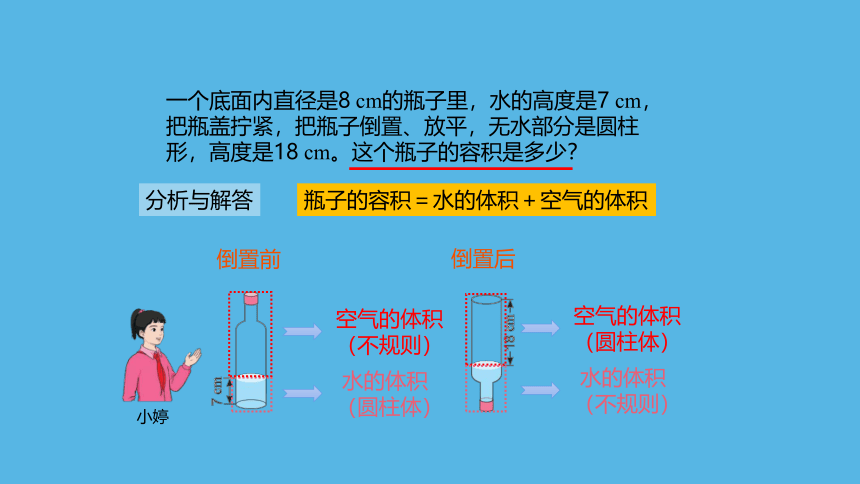
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
阅读与理解
分析与解答
回顾与反思
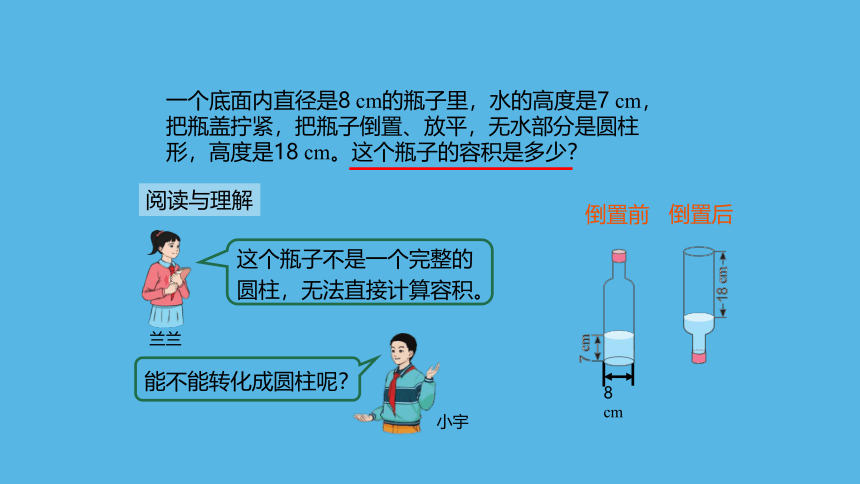
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
这个瓶子不是一个完整的圆柱,无法直接计算容积。
兰兰
8 cm
阅读与理解
倒置前
倒置后
能不能转化成圆柱呢?
小宇
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
借助手边的学具自己试一试,想一想。
老师
分析与解答
8 cm
倒置前
倒置后
分析与解答
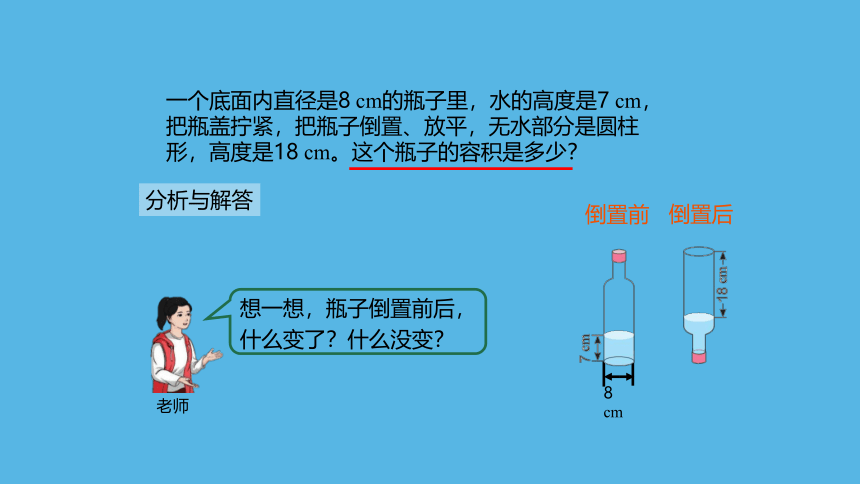
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
想一想,瓶子倒置前后,什么变了?什么没变?
老师
倒置后
瓶子的容积=水的体积+空气的体积
小婷
空气的体积(不规则)
水的体积(圆柱体)
空气的体积(圆柱体)
水的体积(不规则)
分析与解答
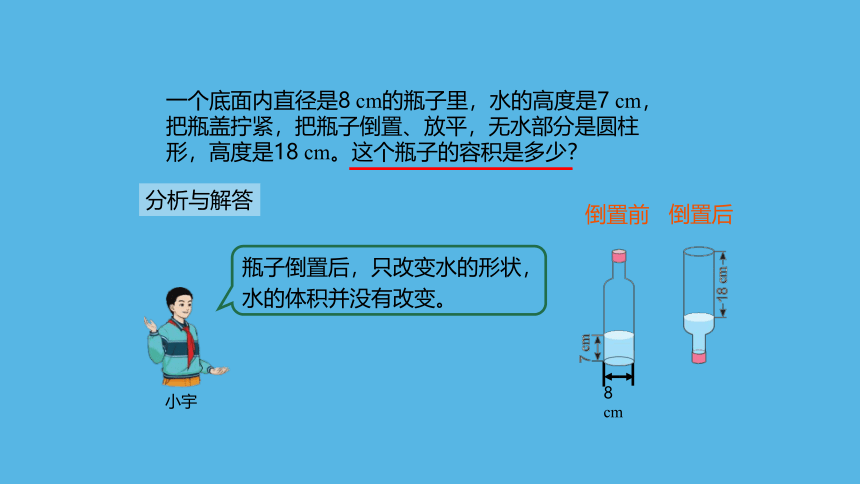
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
倒置前
分析与解答
瓶子倒置后,只改变水的形状,水的体积并没有改变。
小宇
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
瓶子的容积一定,其中水的体积没变,那么,空气的体积也没有发生改变。
瓶子的容积=水的体积+空气的体积(即18 cm高圆柱的体积)
转化
月月
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
倒置前
倒置后
水的体积
不变
空气的体积
变
水的形状
空气的形状
水
空气
转化
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
分析与解答
天天
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
分析与解答
水的体积
空气的体积
小丽
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
分析与解答
兰兰
(7+18)cm
8 cm
7 cm
8 cm
18 cm
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
分析与解答
小婷
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
回顾与反思
回顾与反思
水
空气
转化
小宇
结论:瓶子的容积是1256 mL。
有一瓶装满的矿泉水,瓶子的内直径是6 cm,小明喝了一些,要想知道小明喝了多少水,我们至少还需要测量哪个数据?
通过瓶子的底面直径,求瓶子的底面积,要计算水的体积就需要测量高度。
月月
天天
兰兰
如果测量瓶子倒置前剩下水的高度……
如果测量瓶子倒置后空气的高度……
?
?
10 cm
一瓶装满的矿泉水,瓶子的内直径是6 cm,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10 cm。小明喝了多少水?
小丽
一个装水的圆柱形容器的底面内直径是10 cm,一个铁块完全浸在这个容器的水中,将铁块取出后,水面下降2 cm。这个铁块的体积是多少?
琪琪
2 cm
2 cm
10 cm
我再一次巩固了圆柱体积的计算公式。
把未知转化为已知,把不规则图形转化为规则图形。
应用转化的思想和方法不仅能探索新知识,还能解决新问题。
遇到新问题时,要认真思考,主动应用所学过的知识和方法进行分析和尝试。
收获
文文
小勇
乐乐
小云
数学书第26页
学
习
内
容
1.完成数学书第28页第8题。
2.完成数学书第28页第13题。
课
后
练
习
圆柱的体积(第2课时)
转化
小丽
长方体的底面积等于圆柱的底面积,
圆柱的体积=底面积×高
未知
转化
已知
V = Sh = πr h
长方体的高等于圆柱的高。
水和梨的总体积-水的体积=梨的体积
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
阅读与理解
分析与解答
回顾与反思
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
这个瓶子不是一个完整的圆柱,无法直接计算容积。
兰兰
8 cm
阅读与理解
倒置前
倒置后
能不能转化成圆柱呢?
小宇
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
借助手边的学具自己试一试,想一想。
老师
分析与解答
8 cm
倒置前
倒置后
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
想一想,瓶子倒置前后,什么变了?什么没变?
老师
倒置后
瓶子的容积=水的体积+空气的体积
小婷
空气的体积(不规则)
水的体积(圆柱体)
空气的体积(圆柱体)
水的体积(不规则)
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
倒置前
分析与解答
瓶子倒置后,只改变水的形状,水的体积并没有改变。
小宇
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
瓶子的容积一定,其中水的体积没变,那么,空气的体积也没有发生改变。
瓶子的容积=水的体积+空气的体积(即18 cm高圆柱的体积)
转化
月月
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
倒置前
倒置后
水的体积
不变
空气的体积
变
水的形状
空气的形状
水
空气
转化
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
分析与解答
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
分析与解答
天天
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
分析与解答
水的体积
空气的体积
小丽
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
分析与解答
兰兰
(7+18)cm
8 cm
7 cm
8 cm
18 cm
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
分析与解答
小婷
一个底面内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少?
8 cm
倒置前
倒置后
回顾与反思
回顾与反思
水
空气
转化
小宇
结论:瓶子的容积是1256 mL。
有一瓶装满的矿泉水,瓶子的内直径是6 cm,小明喝了一些,要想知道小明喝了多少水,我们至少还需要测量哪个数据?
通过瓶子的底面直径,求瓶子的底面积,要计算水的体积就需要测量高度。
月月
天天
兰兰
如果测量瓶子倒置前剩下水的高度……
如果测量瓶子倒置后空气的高度……
?
?
10 cm
一瓶装满的矿泉水,瓶子的内直径是6 cm,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10 cm。小明喝了多少水?
小丽
一个装水的圆柱形容器的底面内直径是10 cm,一个铁块完全浸在这个容器的水中,将铁块取出后,水面下降2 cm。这个铁块的体积是多少?
琪琪
2 cm
2 cm
10 cm
我再一次巩固了圆柱体积的计算公式。
把未知转化为已知,把不规则图形转化为规则图形。
应用转化的思想和方法不仅能探索新知识,还能解决新问题。
遇到新问题时,要认真思考,主动应用所学过的知识和方法进行分析和尝试。
收获
文文
小勇
乐乐
小云
数学书第26页
学
习
内
容
1.完成数学书第28页第8题。
2.完成数学书第28页第13题。
课
后
练
习
